Introduction

Nowadays, manufacturing industries make inexorable attempt to achieve the competitive benefit of the design of an optimal layout of facilities. Due to the fact that the facility layout problem (FLP) significantly affects the high manufacturing cost involved in intelligent manufacturing systems, it can be viewed as a crucial issue in the design of modern production systems. Facility layout is the problem of determining the relative locations of facilities on the shop floor. The optimal arrangement of these facilities leads to minimising the total manufacturing cost and maximising the productivity. The Material Handling Cost (MHC) forms 20–50% of the total manufacturing costs and it can be reduced by at least 10–30% by designing an optimal layout (Tompkins et al. 2003). According to the nature of product demands and time planning horizon, the FLP can be classified into four problems as follows: (1) static facility layout problem (SFLP) with deterministic and constant flow of materials over a single time period, (2) dynamic (multi-period) facility layout problem (DFLP) with different deterministic flow of materials in each period, (3) stochastic static facility layout problem (SSFLP) with stochastic flow of materials over a single time period, and (4) stochastic dynamic facility layout problem (SDFLP) where product demands are random variables so that their parameters change from period to period. In the SFLP and SSFLP an optimal layout of facilities is designed so that the total MHC is minimised. On the other hand, for each period of the DFLP and SDFLP an optimal facility layout is designed so that the total material handling and rearrangement costs is minimised. The SDFLP is the most complicated form of the FLP so that the other forms can be regarded as the special case of the problem. In general, the FLP with discrete representation and equal-sized facilities, which are assigned to the same number of locations, can be formulated as the Quadratic Assignment Problem (QAP). In discrete representation, the shop floor is divided into a number of equal-sized locations. Koopmans and Beckman (1957) proposed the first QAP model for the FLP. In this paper, the SDFLP is formulated using a QAP-based mathematical model. Designing the optimal layout of facilities is a crucial competitive advantage of production industries. To find the optimal solution of the FLP formulated by a QAP-based mathematical model, the resolution approaches such as exact methods, heuristic algorithms, and intelligent approaches can be used. Since the QAP is a Non-deterministic Polynomial (NP)-complete problem (Sahni and Gonzalez 1976; Vinoba and Indhumathi 2015), it is very difficult to solve the problem using exact and heuristic methods, especially in large sizes. Thus, it is essential to use intelligent approaches as promising tools for solving the SDFLP formulated by the QAP in a reasonable computational time. Regarding the use of intelligent approaches for solving the DFLP, the following previous researches can be mentioned : Pourvaziri and Naderi (2014) developed a hybrid multi-population Genetic Algorithm (GA) to cope with the DFLP. Azadeh et al. (2014) solved a DFLP having equal-sized facilities using Data Envelopment Analysis (DEA) and diversification strategy of Tabu Search (TS) algorithm. Fazlelahi et al. (2015) suggested a model to design a robust facility layout in dynamic environment utilizing a permutation-based GA. Hasani et al. (2015) proposed a hybrid intelligent approach for solving the DFLP. Derakhshan Asl and Kuan (2015) dealt with static and dynamic FLPs having unequal-sized facilities using a modified Particle Swarm Optimisation (PSO) approach. Bashiri and Karimi (2012) solved a QAP model using some heuristic and meta-heuristic algorithms including SA, TS and PSO approaches. Intelligent approaches are able to find a sub-optimal (near to optimal) solution for the problem at hand. Therefore, there is an urgent need for improving the quality of the obtained solution. Hybrid resolution approaches are common methods to enhance the solution quality of the optimisation problems. Simulated Annealing (SA) is a promising method to solve the FLP especially in volatile environments because it has some advantages such as low computational time, free of local optima, easy for implementation, and convergent property (Moslemipour et al. 2012). Kulturel-Konak and Konak (2015) proposed a simulated annealing meta-heuristic approach to solve a cyclic FLP as a especial case of DFLP where product mix and volume are changed seasonally. Experimental studies on SA demonstrate that selecting a good initial solution for this algorithm leads to improvement in both the obtained solution quality and execution time. Abtahi and Bijari (2017) proposed a hybrid intelligent approach using imperialistic competition, harmony search and SA algorithms.

The first novelty of this paper is proposing a new QAP-based mathematical model for designing an optimal facility layout in each period of the multi-period time planning horizon of the SDFLP. In this model, product demands are assumed to be dependent normally distributed random variables with known Probability Density Function (PDF) and covariance that changes from period to period at random. Product demands have also been considered as normally distributed or at least random variables in layout design problems in a number of previous studies (Forghani et al. 2013; Nematian 2014; Vafaeinezhad et al. 2016; Vitayasak et al. 2016; Zhao and Wallace 2014, 2015). The second novelty of this paper is suggesting a new hybrid algorithm named CS-SA for solving the SDFLP by combining the Clonal Selection (CS), and SA algorithms. In this algorithm, a population of randomly generated initial solutions is improved using the CS algorithm. By doing so, the performance of the SA algorithm is likely to be improved from both solution quality and computational time points of view.

Literature review

Hitchings (1970) considered dynamic behaviour of the FLP for the first time. Palekar et al. (1992) designed the SDFLP using quadratic integer programming model. They considered three degrees of uncertainties named optimistic, most likely, and pessimistic for product demands by assigning probability of happenings to these degrees. Montreuil and Laforge (1992) addressed the SDFLP using a scenario tree of probable futures. In their method, a number of alternative layouts were built for future. Krishnan et al. (2008) proposed three mathematical models for designing a facility layout in an uncertain environment by considering multiple product demand scenarios. Tavakkoli-Moghaddam et al. (2007) suggested a novel formulation using the QAP to concurrent design of the optimal machine and cell layouts in a single time period planning horizon of a cellular manufacturing system (CMS) by considering the stochastic independent product demands with known normal PDF. Moslemipour and Lee (2012) proposed a new QAP-based mathematical model for designing an optimal machine layout for each period of the SDFLP, in which the product demands are independent normally distributed random variables with known PDF that changes from period to period at random. In this paper, in addition to the aforementioned assumptions, time value of money and dependency of product demands are also considered so that the expectation, variance and covariance of demands are randomly changed from period to period. Shafigh et al. (2015) proposed a novel mathematical model for designing dynamic distributed layouts.

Clonal selection algorithm

CS algorithm belongs to Artificial Immune System (AIS) approaches. The biological immune system protects the human body against foreign invaders such as viruses and bacteria called antigens. The molecules named antibodies, which recognise the presence of an antigen, are rapidly increased by cloning during the clonal selection process. The affinity of the new cloned antibodies is improved by mutations, which in turn, leads to neutralisation and elimination of the antigen. The probability of selecting antibodies for mutation is proportional to their affinity to the antigen. After mutation, the receptor editing process is started by eliminating some percentage of the ineffective antibodies and introducing the same percentage of the new ones. The simulation of the natural immune system leads to development of a new intelligent algorithm named AIS. The AIS starts with a randomly generated population of individuals (antibodies) as the possible solutions. At each iteration of this algorithm, first, the affinity of each antibody is calculated using the objective function of the problem. Next, a number of antibodies with the best affinity value are selected and cloned. Then, each clone is mutated and the improved antibodies are preserved for the next generation. Finally, using the receptor editing process, a pre-specified number of antibodies with low affinity values are replaced with the new ones, which are generated at random. Ulutas and Islier (2009) proposed a CS algorithm for solving the DFLP. Satheesh Kumar et al. (2009) proposed an AIS algorithm to solve the unidirectional loop layout problem by minimising the total congestion of all parts and minimising the maximum congestion amongst a partfamily. Ulutas and Kulturel-Konak (2012) suggested a CS algorithm to deal with a FLP having unequal-sized facilities and flexible bay arrangement. Ulutas and Kulturel-Konak (2013) suggested an improved CS algorithm for designing the FLP with unequal-sized facilities. They proposed a novel encoding method and a guideline for optimising the parameters of the CS algorithm. Ulutas and Islier (2015) proposed a CS algorithm for solving a real DFLP named footwear industry.

In this paper, the CS algorithm is utilised to improve the quality of randomly generated initial solutions. The initial solutions are applied to SA algorithm described in the following section. Doing so, a hybrid algorithm named CS-SA is constructed so that it has an outstanding performance from both solution quality and computational time points of view with respect to the SA having just a single initial solution.

Simulated annealing algorithm

SA algorithm is a simulation of physical annealing process of solids in statistical mechanics, which starts with a known or randomly generated initial solution and a high initial value of temperature. It is formed by two loops namely, the inner loop to search for a neighbouring solution, and the outer loop for decrease the temperature to reduce the probability of accepting the non-improving neighbouring solutions in the inner loop. The quality of the solution obtained by SA depends upon various factors such as initial temperature, initial solution, and the exchange approach for generating neighbouring solutions in the inner loop. Due to the fact that SA is a single search algorithm, the quality of its final solution is affected by the initial solution (Ashtiani et al. 2007; Chen and Jing 2005). Using hybrid algorithms, the disadvantage of some algorithms are compensated by the advantage of some other ones. Ram et al. (1996) proposed two distributed algorithm namely, Clustering Algorithm (CA) and Genetic Clustering Algorithm (GSA), which generate a good initial solution and a good population of initial solutions for SA algorithm, respectively. They applied the two algorithms to the Job Shop Scheduling (JSS) problem and the Travelling Salesman Problem (TSP) and concluded that the performance of SA was improved from both computational time and solution quality standpoints. Ashtiani et al. (2007) developed multiple initial solutions for SA approach to solve the DFLP. Dong et al. (2009) used SA algorithm to solve the DFLP by considering the possibility of removing/adding facilities in different periods. Rezazadeh et al. (2009) and Tajbakhsh et al. (2009) combined SA algorithm with PSO method to solve the FLP. Sahin et al. (2010) used SA algorithm to deal with the DFLP by regarding budget constraint. Madhusudanan-Pillai et al. (2011) solved their proposed robust layout design model using SA in DFLP. Moslemipour and Lee (2012) utilised SA algorithm to solve their developed model in the SDFLP. Lee et al. (2012) proposed a novel hybrid Ant Clony (AC)/SA approach having outstanding performance to solve the SDFLP. Moslemipour et al. (2012) reviewed intelligent approaches for solving layout problems comprehensively. Khosravian-Ghadikolaei and Shahanaghi (2013) proposed a solution approach based on SA algorithm for solving the multi-floor DFLP. Shirazi et al. (2014) developed a multi-objective SA-based algorithm to deal with a group layout. Li et al. (2015) suggested an improved SA algorithm for designing the SDFLP. Palubeckis (2015) dealt with the single row facility layout problem by proposing a fast SA algorithm having better performance than the iterated TS algorithm. Palubeckis (2016) also proposed a multi-start SA approach to design the single row facility layout. Kulturel-Konak and Konak (2015) developed a large-scale hybrid SA algorithm for solving the cyclic FLP as a special case of the DFLP, which is formulated by a Mixed Integer Programming (MIP) model. In the cyclic FLP, the production cycle replicate itself by going to the first time period after the last one owing to the seasonal feature of products. Matai (2015) developed an improved SA algorithm for solving the FLP. Tayal and Singh (2016) used a hybrid meta-heuristic approach, which is based on Firefly and Chaotic SA algorithms for solving the multi-objective SDFLP by considering stochastic demands. Tayal and Singh (2017) proposed an integrated resolution approach by combining the SA algorithm with the DEA and TOPSIS as practical decision-making methods for solving a multi-objective SDFLP. They considered some quantitative and qualitative objectives, such as total MHC, flow distance, closeness ratio and maintenance issues.

The proposed model

The QAP is a nonlinear Combinatorial Optimisation Problem (COP). This problem aims to find the optimum appointing of several items to the same number of known positions so that a quadratic objective function is minimised. In general, the FLP having discrete representation and equal-sized facilities assigned to the same number of known locations is usually formulated by the QAP model. In discrete representation, the shop floor is divided into a number of equal-sized facility locations. In this section, the SDFLP is formulated by a new QAP-based mathematical model to design the dynamic machine layout. The parameters and indexes used in the models are shown in Table 1.

Table 1 Notations of the proposed models
Full size table

The assumptions are as follows:

  1. 1.

    Equal-sized facilities (machines) are assigned to the same number of known locations.

  2. 2.

    The discrete representation of the SDFLP is considered.

  3. 3.

    For simplicity, it is assumed that demands of a particular part in different time periods are independent of each other (i.e. \({\text{Cov}}\left( {D_{tk} ,D_{{t^{\prime}k}} } \right) = 0\)). Shumsky and Zhang (2009), for instance, has already made this assumption.

  4. 4.

    Demands of products are assumed to be dependent (i.e. \({\text{Cov}}(D_{tk} ,D_{{tk^{\prime}}} ) \ne 0\)) normally distributed random variables with known expected value, variance, and covariance that change from period to period at random.

  5. 5.

    The parts are moved in batches between facilities.

  6. 6.

    Time value of money is considered.

  7. 7.

    There is no constraint for dimensions and shapes of the shop floor.

  8. 8.

    The data on number of facilities, number of periods, machine sequence, present value of part movement cost, transfer batch size, distance between facility locations, money interest rate for each period (e.g., year), present value of facility rearrangement cost, the expected value, variance, and covariance of part demands in each period are known as inputs of the model.

  9. 9.

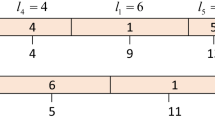
    Machines can be laid out in any configuration such as rectangular and U-shaped configurations as shown in Fig. 1, where L1,…, L12 are the known machine locations.

    Fig. 1
    figure 1

    a Rectangular configuration and b U-shaped configuration

    Full size image

Designing a dynamic facility layout is a method to cope with fluctuations and uncertainties in product demands in the SDFLP. In the dynamic layout design method, an optimal layout is designed for each period so that the total cost including the MHC and the relocation cost is minimised. Using this approach, the layout of facilities can be changed from period to period in accordance with changes in product demands. Therefore, although this method has the advantage of having optimal layout for each period, it suffers from the disadvantage of having the facility rearrangement cost. Actually, in the dynamic approach, considering each period as a stage, the multi-period problem can be considered as a multi-stage dynamic system with optimal behaviour from stage to stage. In this section, the SDFLP is formulated using the dynamic approach so that an optimal machine layout is obtained for each period. According to the assumption of assigning the equal-sized machines to the same number of known locations, the QAP model of the DFLP proposed by Balakrishnan et al. (1992) is used for formulating the SDFLP. This model is given in equations from (1)–(5).

$${\text{Minimize}}\sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {f_{tij} } } } } d_{lq} x_{til} x_{tjq} } + \sum\limits_{t = 2}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {a_{tilq} } } } } y_{tilq}$$
(1)

Subject to:

$$\sum\limits_{i = 1}^{M} {x_{til} } { = 1 ; \forall }t\text{,}l$$
(2)
$$\sum\limits_{l = 1}^{M} {x_{til} } { = 1 ; \forall }t\text{,}i$$
(3)
$$x_{til} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\;{\text{facility}}\;i\;{\text{is}}\;{\text{assigned}}\;{\text{to}}\;{\text{location}}\;l\;{\text{in}}\;{\text{period}}\;t} \hfill \\ 1 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(4)
$$y_{tilq} = x_{{\left( {t\text{ - 1}} \right)il}} { \times }x_{tiq}$$
(5)

where, f tij denotes the total materials current in period t from facility i to facility j and vice versa. The distance between facility locations l and q is represented by d lq . The fixed cost of shifting facility i from location l to location q in period t is denoted by a tilq . The objective function given in Eq. (1) is the sum of two terms, including the total MHC and the total rearrangement cost. The constraints (2) and (3) ensure assigning each facility in each period to exactly one location and vice versa. Equation (4) represents the decision variables that are the solutions to the problem so that they determine the location of each facility in each period. Equation (5) indicates that \(y_{tilq} = 1\) if the facility i is shifted from location l in period t − 1 (i.e. \(x_{{\left( {t - 1} \right)il}} = 1\)) to location q in period t (i.e. \(x_{tiq} = 1\)). The flow of materials linking machines i and j in period t created by part k can be calculated using Eq. (6), where the condition |N k  − N kj | = 1 refers to two consecutive operations, which are done on part k by machines i and j. Since the demand is divided by the batch size, the quantity of the flow should be discrete value. As mentioned in the assumptions of the problem, the demand for part k in period t (\(D_{tk}\)) is a random variable with normal distribution. Therefore, according to Eq. (6), the materials current created by part k in period t from facility i to facility j and vice versa (\(f_{tijk}\)) is also a random variable with a normal distribution having the expectation and variance given in Eqs. (7) and (8), respectively.

$$f_{tijk} = \left\{ {\begin{array}{*{20}l} {\frac{{D_{tk} }}{{B_{k} }}C_{tk} } \hfill & \quad{{\text{if}}\;N_{ki} - N_{kj} \; = \;1} \hfill \\ 0 \hfill &\quad {{\text{otherwis}}e} \hfill \\ \end{array} } \right.$$
(6)
$$E_{tijk} = \left\{ {\begin{array}{*{20}l} {\frac{{D_{tk} }}{{B_{k} }}C_{tk} } \hfill &\quad {{\text{if}}\;N_{ki} - N_{kj} \; = \;1} \hfill \\ 0 \hfill &\quad {{\text{otherwis}}e} \hfill \\ \end{array} } \right.$$
(7)
$${\text{Var}}_{tijk} = \left\{ {\begin{array}{*{20}l} {\frac{{D_{tk} }}{{B_{k}^{2} }}C_{tk}^{2} } \hfill &\quad {{\text{if}}\;N_{ki} - N_{kj} \; = \;1} \hfill \\ 0 \hfill &\quad {{\text{otherwis}}e} \hfill \\ \end{array} } \right.$$
(8)

The total materials current linking machines i and j in period t created by all parts (i.e. f tij ) is obtained using Eq. (9) in which \(f_{tijk}\) is a random variable with normal distribution and thereby \(f_{tij}\) is also a random variable with a normal distribution having the expectation and variance shown in Eqs. (10) and (11), respectively. According to assumption (4), in each period, demands of parts are dependent. It means that \(Cov(D_{tk} ,D_{{tk^{\prime}}} ) \ne 0\) and thereby \(cov(f_{tijk} ,f_{{tijk^{\prime}}} ) \ne 0\). Kulturel-Konak et al. (2004) has already used an equation similar to Eq. (11), but for a single period problem. Inserting Eqs. (7) and (8) into Eqs. (10) and (11) leads to the new form of the expectation and variance of \(f_{tij}\) as represented in Eqs. (12) and (13), respectively. Utilising Eqs. (1) and (5), the total cost for a given dynamic machine layout π dm, which is denoted by C(π dm), is calculated using Eq. (14). In this equation, the total cost is equal to the summation of the total MHC (the first term) and the total rearrangement cost (the second term).

$$f_{tij} = \sum\limits_{k = 1}^{K} {f_{tijk} }$$
(9)
$$E\left( {f_{tij} } \right) = \sum\limits_{k = 1}^{K} {E\left( {f_{tijk} } \right)}$$
(10)
$${\text{Var}}\left( {f_{tij} } \right) = \sum\limits_{k = 1}^{K} {{\text{Var}}\left( {f_{tijk} } \right)} + 2\sum\limits_{k = 1}^{K} {\sum\limits_{{k^{\prime} = k + 1}}^{K} {{\text{cov}}(f_{tijk} ,f_{{tijk^{\prime}}} )} }$$
(11)
$$E\left( {f_{tij} } \right) = \sum\limits_{k = 1}^{K} {\frac{{E\left( {D_{tk} } \right)}}{{B_{k} }}C_{tk} }$$
(12)
$${\text{Var}}\left( {f_{tij} } \right) = \sum\limits_{k = 1}^{K} {\frac{{{\text{Var}}\left( {D_{tk} } \right)}}{{B_{k}^{2} }}C_{tk}^{2} } + 2\sum\limits_{k = 1}^{K} {\sum\limits_{{k^{\prime} = k + 1}}^{K} {\frac{{C_{tk} C_{{tk^{\prime}}} }}{{B_{k} B_{{k^{\prime}}} }}} } {\text{cov}}(D_{tk} ,D_{{tk^{\prime}}} )$$
(13)
$$C\left( {\pi_{\text{dm}} } \right) = \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {f_{tij} } } } } d_{lq} x_{til} x_{tjq} } + \sum\limits_{t = 2}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {a_{tilq} } } } } x_{{\left( {t - 1} \right)il}} x_{tiq}$$
(14)

Since f tij is a random variable with normal distribution, then according to Eq. (14), C(π dm) is also a normally distributed random variable (Braglia et al. 2005). Using Eq. (14), the expected value and variance of C(π dm) are given in Eqs. (15) and (16), respectively. According to the assumption (3), demands of a particular part in different time periods are independent. It means that \({\text{Cov}}\left( {D_{tk} ,D_{{t^{\prime}k}} } \right) = 0\) and thereby in Eq. (16), \({\text{Cov}}\left( {f_{tij} ,f_{{t^{\prime}ij}} } \right) = 0\), but as earlier mentioned, \({\text{Cov}}(D_{tk} ,D_{{tk^{\prime}}} ) \ne 0\).

$$E\left( {C\left( {\pi_{\text{dm}} } \right)} \right) = \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {E\left( {f_{tij} } \right)\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {d_{lq} } } } } x_{til} x_{tjq} } + \sum\limits_{t = 2}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {a_{tilq} } } } } x_{{\left( {t - 1} \right)il}} x_{tiq}$$
(15)
$${\text{Var}}\left( {C\left( {\pi_{\text{dm}} } \right)} \right) = \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {{\text{Var}}\left( {f_{tij} } \right)\left( {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {d_{lq} x_{til} x_{tjq} } } } \right)^{2} } } }$$
(16)

Since we consider time value of money, C tk and a tilq can be calculated using Eqs. (17) and (18), respectively. In these equations, C k is the present value of the movement cost for part k, a 0ilq is the present value of a tilq and I r is the interest rate for each period. Using Eqs. (12), (13), (15), (16), (17), and (18), the new form of the expectation and variance of the total cost are given in Eqs. (19) and (20), respectively. For a given dynamic machine layout π dm if the decision maker considers U(π dm, p) as the maximum value (upper bound) of C(π dm) with the confidence level p, then U(π dm, p) given in Eq. (21) can be minimised instead of minimising C(π rm ) (Kulturel-Konak et al. 2004; Moslemipour and Lee 2012; Norman and Smith 2006; Tavakkoli-Moghaddam et al. 2007)

$$C_{tk} = C_{k} (1 + I_{r} )^{t}$$
(17)
$$a_{tilq} = a_{0ilq} (1 + I_{r} )^{t}$$
(18)
$$E\left( {C\left( {\pi_{\text{dm}} } \right)} \right) = \left( \begin{aligned} \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {\frac{{E\left( {D_{tk} } \right)}}{{B_{k} }}C_{k} (1 + I_{r} )^{t} } \sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {d_{lq} } } } } x_{til} x_{tjq} } + \hfill \\ \sum\limits_{t = 2}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {a_{tilq} } } } } x_{{\left( {t - 1} \right)il}} x_{tiq} \hfill \\ \end{aligned} \right)$$
(19)
$${\text{Var}}\left( {C\left( {\pi_{\text{dm}} } \right)} \right) = \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {\left( \begin{aligned} \frac{{{\text{Var}}\left( {D_{tk} } \right)}}{{B_{k}^{2} }}C_{k}^{2} (1 + I_{r} )^{2t} + \hfill \\ 2\sum\limits_{k = 1}^{K} {\sum\limits_{{k^{\prime} = k + 1}}^{K} {\frac{{C_{k} C_{{k^{\prime}}} }}{{B_{k} B_{{k^{\prime}}} }}(1 + I_{r} )^{2t} } } {\text{cov}}(D_{tk} ,D_{{tk^{\prime}}} ) \hfill \\ \end{aligned} \right)} \left( {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {d_{lq} x_{til} x_{tjq} } } } \right)^{2} } } }$$
(20)
$$U\left( {\pi_{\text{dm}} ,p} \right)\text{ = }E\left( {C\left( {\pi_{\text{dm}} } \right)} \right)\text{ + }Z_{p} \sqrt {{\text{Var}}\left( {C\left( {\pi_{\text{dm}} } \right)} \right)}$$
(21)

The mathematical model to obtain the optimal layout of machines for each period of the SDFLP can be written as follows using Eqs. (19), (20) and (21):

Minimisation of

$${\text{OFV}}_{\text{dm}} = \left\{ \begin{aligned} \sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {\frac{{E\left( {D_{tk} } \right)}}{{B_{k} }}C_{k} (1 + I_{r} )^{t} } \sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {d_{lq} } } } } x_{til} x_{tjq} } + \hfill \\ Z_{p} \sqrt {\sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{M} {\sum\limits_{k = 1}^{K} {\left( \begin{aligned} \frac{{{\text{Var}}\left( {D_{tk} } \right)}}{{B_{k}^{2} }}C_{k}^{2} (1 + I_{r} )^{2t} + \hfill \\ 2\sum\limits_{k = 1}^{K} {\sum\limits_{{k^{\prime} = k + 1}}^{K} {\frac{{C_{k} C_{{k^{\prime}}} }}{{B_{k} B_{{k^{\prime}}} }}(1 + I_{r} )^{2t} } } {\text{cov}}(D_{tk} ,D_{{tk^{\prime}}} ) \hfill \\ \end{aligned} \right)} } } } } \left( {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {d_{lq} x_{til} x_{tjq} } } } \right)^{2} + \hfill \\ \sum\limits_{t = 2}^{T} {\sum\limits_{i = 1}^{M} {\sum\limits_{l = 1}^{M} {\sum\limits_{q = 1}^{M} {a_{tilq} } } } } x_{{\left( {t - 1} \right)il}} x_{tiq} \hfill \\ \end{aligned} \right\}$$
(22)

Subject to: Equations from (2)–(4)

Proposed the CS-SA hybrid algorithm to solve the SDFLP

Due to the fact that SA is a single search algorithm, the solution quality and computational time are affected by the initial solution. In addition, it is a well-known local search technique, which has been used to improve the quality of a known initial solution generated by other algorithms. Therefore, in the proposed hybrid algorithm, to conquer the reliance of SA on initial solution, a population of initial solutions is used rather than one initial solution. The proposed hybrid CS-SA algorithm contains three stages as follows: (1) generating a population of feasible initial solutions (antibodies) randomly, (2) selecting and cloning the antibodies produced in the first stage using the CS algorithm, and (3) improving the cloned antibodies using SA algorithm. The notations used in this section are shown in Table 2 apart from the ones given in Table 1. The three above-mentioned stages are described in the following sub-sections.

Table 2 Notations for CS-SA algorithm
Full size table

Stage 1: initial solution construction

It is essential to state that in the CSA, antibodies are potential solutions of the problem. In this stage, a population of the potential initial solutions consists of the antibodies are randomly generated and the number of antibodies is defined as the population size. It is assume that the population size to be equivalent of the number of time periods (T) in the SDFLP. In this stage, T initial solutions are randomly generated during the two following stepes:

Step 1: select T permutations of 1, 2, …, M as the first row of T matrices

Step 2: to consider each of the permutations for all periods

Each of the T partial solutions (layouts) constructed in Step 1 are considered for all periods in Step 2. By doing so, a population of initial solutions with size T is constructed for the SDFLP. It is necessary to mention that a solution of the SDFLP is represented by a two dimensional matrix where each row represents a period, each column represents a location, and each element represents a machine number. For example, for a dynamic layout problem having three time periods and three facilities including machines 1, 2, and 3, the population of initial solutions can be in the following form:

$${\text{Population}}\;{\text{of}}\;{\text{initial}}\;{\text{solutions}} = \left\{ {s_{1}^{0} ,s_{2}^{0} ,s_{3}^{0} } \right\} = \left\{ {\left[ {\begin{array}{*{20}c} 3 & 1 & 2 \\ 3 & 1 & 2 \\ 3 & 1 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 1 & 3 & 2 \\ 1 & 3 & 2 \\ 1 & 3 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 2 & 1 & 3 \\ 2 & 1 & 3 \\ 2 & 1 & 3 \\ \end{array} } \right]} \right\}$$

Stage 2: selection and cloning antibodies

As mentioned in section “Clonal selection algorithm”, CS is a population-based algorithm. Therefore, the population of initial solutions constructed in Stage 1 can be easily applied to the CS algorithm. In this stage, only the selection and cloning steps of CS are used to amplify the power of the good initial solutions constructed in the first stage. Therefore, a number of the best initial antibodies are selected and cloned according to their affinity value. The affinity of the initial solution (antibody) s 0 i is defined as the inverse of its objective function value as given in Eq. (23). In this approach, better antibodies have the higher value of affinity.

$${\text{Affinity}}(s_{i}^{0} ) = \frac{1}{{f(s_{i}^{0} )}}$$
(23)

During selection process, n (n < T) best antibodies having the highest affinity values are selected for cloning. Actually, the affinity values of the best n antibodies are sorted in descending order. Doing so, for i < j, Affinity (s 0 i ) > Affinity (s 0 j ). Using cloning process, the selected antibodies are cloned according to Eq. (24) extracted from De Castro and Von Zuben (2002) so that the antibody with higher affinity value has higher number of clones.

$${\text{NC}}_{i} = {\text{round}}\left( {\frac{\delta *n}{i}} \right)$$
(24)

where, i denotes the rank of antibody (for the antibody with the highest affinity i = 1), NC i is the number of clones for antibody s 0 i , δ is a size factor (Here, δ = 1), n is the number of selected antibodies, and round refers to the closest integer. Using this approach, the size of the new population would be the summation of NC i .

To illustrate the aforementioned procedure, we consider the example of a population of initial solutions given in section 4.1. We assume that the initial solutions are arranged in descending order so that Affinity (s 0 1 ) > Affinity (s 0 2 ) > Affinity (s 0 3 ). It is also assumed that all of the initial solutions are selected (i.e., n = T = 3). According to the order of the initial solutions, the rank of s 0 1 , s 0 2 , and s 0 3 (i.e., i in Eq. (24)) will be 1, 2, and 3, respectively. Thus, using Eq. (24), the number of clones (NC i ) for the initial solutions (antibodies) s 0 1 , s 0 2 , and s 0 3 are equals to 3, 2, and 1, respectively. By doing so, the final population of initial solutions (antibodies), which is applied to the SA algorithm in the next stage, is as follows:

$$\left\{ {\left[ {\begin{array}{*{20}c} 3 & 1 & 2 \\ 3 & 1 & 2 \\ 3 & 1 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 3 & 1 & 2 \\ 3 & 1 & 2 \\ 3 & 1 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 3 & 1 & 2 \\ 3 & 1 & 2 \\ 3 & 1 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 1 & 3 & 2 \\ 1 & 3 & 2 \\ 1 & 3 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 1 & 3 & 2 \\ 1 & 3 & 2 \\ 1 & 3 & 2 \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} 2 & 1 & 3 \\ 2 & 1 & 3 \\ 2 & 1 & 3 \\ \end{array} } \right]} \right\}$$

CS also includes mutation and receptor editing processes used for solution improvement and to avoid from getting trapped in local optima, respectively. However, in this stage, there is no need to use the aforementioned processes. Because they are done in the third stage of the hybrid algorithm (i.e., SA algorithm). In the inner loop of SA algorithm, the solution is improved by searching for a better neigbouring solution and accepting non-improving neigbouring solutions prevents the algorithm from getting trapped in local optima.

Stage 3: initial solutions improvement

In this stage as the last part of the hybrid algorithm, SA algorithm is used to find the optimal solution of the problem at hand. In the proposed hybrid algorithm, to conquer the reliance of SA on initial solution, a population of cloned initial solutions is used rather than one initial solution. Thus, the cloned initial solutions (antibodies) constructed by the two previous stages, are applied to the SA algorithm according to their order in the population. By doing so, the first initial solution, which has the highest affinity, is the starting initial solution. In general, SA starts with the initial solution s 0 and a high initial temperature T in . As mentioned, the solutions are in the form of matrix and the SA algorithm consists of two loops, including inner loop and outer loop. At each iteration of the inner loop, a neighbouring solution s′ for the best current solution s, which is obtained in the previous iteration, is generated using the local search technique named random exchange method. In this method, first, a row (period) is selected at random. Then, two columns (locations) are randomly selected. Finally, the elements (machines) in the two locations are exchanged. The solution s′ is evaluated by the objective function f given in Eq. (2). It is accepted as the current best solution if \(f\left( {s^{{\prime }} } \right) \le f\left( s \right)\). In the case of \(f\left( {s^{{\prime }} } \right)\text{ > }f\left( s \right)\) it is also accepted if \(x \in \left( {0,1} \right) \le P_{el}\), where x is a randomly generated number and P el is the probability of accepting this non-improving neighbouring solution s′ at iteration el of the outer loop. The outer loop starts with a high value of temperature. At each iteration of this loop or in other words, at each temperature, the inner loop is repeated until the system reaches the steady state or thermal equilibrium. In this paper, for solving the SDFLP with M facilities (machines) and T periods, the maximum number of iterations for the inner loop il max is calculated by Eq. (25).

$$il_{\hbox{max} } = \varphi \times M \times T$$
(25)

where, experimentally, φ = 0.5 for small-sized problems. It is increased proportional to the size of problem. The temperature is gradually reduced by running the outer loop so that its current value in the iteration el of this loop is calculated using Eq. (26), where, \(\theta \in \left( {0.80,0.99} \right)\) is the cooling ratio (here, \(\theta = 0.95\)), \(el_{\hbox{max} }\) denotes the maximum number of iterations of the outer loop, and T in denotes the initial value of the temperature. According to McKendall et al. (2006), the initial temperature is calculated by Eq. (27).

$$T_{el} = T_{\text{in}} \theta^{el} ;\quad \left( {el = 0,1, \ldots ,el_{\hbox{max} } } \right)$$
(26)
$$T_{\text{in}} = - \frac{{0.1f(s^{0} )}}{\ln (0.25)}$$
(27)

The probability of accepting the non-improving solution is given in Eq. (28). Using Eq. (28), the value of temperature at iteration el (i.e. T el ) can be calculated by Eq. (29). Using Eq. (29), the initial temperature T in and final temperature T f are given in Eqs. (30) and (31), respectively, where, P in and P f are the initial and final values of P el . Using Eqs. (30) and (31), Eq. (32) can be written. The maximum number of iterations of the outer loop el max corresponds to T f can be calculated using Eq. (33) that can be rewritten as Eq. (34). In fact, in Eq. (26), if we put \(T_{el} = T_{f}\) and \(el = el_{\hbox{max} }\) then Eq. (33) is obtained. The Eq. (33) can be rearranged as Eq. (34). The final form of Eq. (34) can be written as Eq. (35) using Eqs. (30) and (31).

$$P_{el} =\, e^{{\frac{{f\left( s \right)\text{ - }f\left( {s{\prime }} \right)}}{{T_{el} }}}}$$
(28)
$$T_{el} = \,\frac{{f\left( s \right)\text{ - }f\left( {s{\prime }} \right)}}{{\ln (P_{el} )}}$$
(29)
$$T_{\text{in}} =\, \frac{{f\left( s \right)\text{ - }f\left( {s{\prime }} \right)}}{{\ln (P_{\text{in}} )}}$$
(30)
$$T_{\text{f}} = \,\frac{{f\left( s \right)\text{ - }f\left( {s{\prime }} \right)}}{{\ln (P_{\text{f}} )}}$$
(31)
$$T_{\text{f}} = T_{\text{in}} \left( {\ln \frac{{P_{\text{in}} }}{{P_{\text{f}} }}} \right)$$
(32)
$$T_{\text{f}} = T_{\text{in}} \theta^{{el_{\hbox{max} } }}$$
(33)
$$el_{\hbox{max} } = \log_{\theta } \left( {\frac{{T_{\text{f}} }}{{T_{\text{in}} }}} \right)$$
(34)
$$el_{\hbox{max} } = \log_{\theta } \left( {\ln \frac{{P_{\text{in}} }}{{P_{\text{f}} }}} \right)$$
(35)

The probability of accepting the non-improving solution \(P_{el}\) is high at the initial stages of the algorithm (\(P_{\text{in}} \approx 1\)) and it is reduced gradually while the algorithm is repeated so that it approaches to a very small value at the final stages of the algorithm (\(P_{\text{f}} \approx 0\)). Finally, the Pseudocode of proposed hybrid is shown in Fig. 2.

Fig. 2
figure 2

The pseudocode of the hybrid CS-SA algorithm

Full size image

Qualitative analysis of the CS-SA algorithm

In this section, the performance of the proposed hybrid algorithm is investigated from both of the solution quality and computational time points of view in a qualitative manner. In other words, it will be explained that how the good initial solutions generated by CS lead to improve both of the solution quality and the computational time of SA algorithm. First, the effect of the randomly generated initial solutions improved by CS algorithms on the computational time of the SA is investigated. To this end, the maximum number of iterations of the outer and the inner loops of the SA is considered.

To estimate the maximum number of iterations of the outer loop (el max) of the SA used in the proposed hybrid algorithm, we assume that, \(P_{\text{in}} = 0.95\), \(P_{\text{f}} = 10^{ - 15}\) and \(\theta = 0.95\) (Baykasogylu and Gindy 2001). Doing so, it is calculated as \(el_{\hbox{max} } \approx 127\) using Eq. (35). According to Eq. (30), in the proposed algorithm, starting SA algorithm with a better initial solution s 0 generated by CS leads to lower value of the cost function f(s 0) and in turn causes to decrease the initial temperature T in. Referring to Eq. (34), decrease in the initial temperature results in decrease in the maximum number of the outer loop iterations. Therefore, the maximum number of iterations of the outer loop of the SA used in the hybrid algorithm is less than the above-mentioned estimated value (i.e., \(el_{\hbox{max} } \approx 127\)). Starting the inner loop of the SA with a good initial solution drives the algorithm to search for a better solution in the neighbouring area of the good solution. Doing so, the local search technique used in the inner loop of SA is reached to a frozen (equilibrium) state very fast. When a frozen state is reached, the chance of finding new better solutions is quite small (Heragu 1997). In other words, there is no improvement in the solution quality after several iterations. Therefore, using the good initial solutions the maximum number of iterations of the inner loop (il max) is also reduced.

Due to reduction in both of the el max and the il max, the SA algorithm converges to a global optimal solution faster than the case in which it starts with only one known or randomly generated initial solution. As a result, the computational time elapsed by the SA algorithm is decreased by starting with a population of good initial solutions constructed by CS algorithm.

The good initial solutions constructed by CS algorithm also result in improvement in the quality of the final solution obtained by the SA algorithm. As mentioned, in SA algorithm, the quality of solution is improved by searching for a neighbouring solution using a local search technique. This technique is amplified by starting the SA algorithm with a good initial solution. Because, by doing so, the local search technique forces the algorithm to search in the neighbouring area of the good solution to hope to find a better solution. The quality of the neighbourhood solution affects the success of the local search method. Actually, this process behaves like the intensification strategy, which is used in other metaheuristics, for instance, in the TS algorithm. The intensification strategy drives the algorithm to search for a better solution in the neighbouring area of the good solution. As a result, amplification of the local search technique by starting with good initial solution leads to improve the quality of the final solution of SA algorithm. The proposed hybrid algorithm is generic that can be used to solve any forms of the mathematical models of the FLP, which can be different by considering some critical constraints such as using unequal-sized machines, the shop floor with different dimensions and shapes. Since initial solutions constructed by the CS algorithm are improved using a local search technique such as random pair-wise exchange method used in the SA algorithm, they are subject to randomly change at each iteration of the SA method. Therefore, the initial solutions are not affected by some constraint such as the case that two facilities can not be placed consecutively, and budget constraint. Instead, such constraints should be considered in the third stage (i.e. SA algorithm) of the hybrid algorithm.

Computational results and discussion

In this section, to validate the proposed model and also to evaluate the performance of the proposed hybrid CS-SA algorithm, design of experiment and benchmark methods are used as explained in the two following sub-sections:

Design of experiment

In this section, design of experiment method is utilised to verify and validate the proposed model and the hybrid CS-SA algorithm, which is proposed for solving the SDFLP. To this end, a large number (say, 1000) of randomly generated test problems are applied to the model and solved using the the hybrid CS-SA algorithm. A personal computer with Intel 2.10 GHZ CPU and 3 GB RAM is used to run the hybrid and SA algorithms, which are programmed in Matlab. Since there is no historical data on expectation and variance of demands in each period, design of experiment method is used to evaluate the performance of the proposed CS-SA hybrid algorithm. To this end, 1000 randomly generated test problems are applied to the dynamic machine layout design model given in Eq. (22) and solved using the proposed hybrid CS-SA and the SA algorithms. Actually, the performance of the SA algorithm starting with a population of initial solutions, which is generated by the CS algorithm, is compared with the performance of the SA algorithm starting with a single known initial solution. Each test problem has the following input data: Expectation and variance of parts demand (E and V) are randomly generated with uniform distribution so that \(E \in (1000,10000)\) and \(V \in (1000,3000)\). The distance matrix is given in Table 3. The number of machines and the number of periods are twelve and ten (M = 12, T = 10), respectively. The facility rearrangement cost (a tilq ) is equal to 1000. In Eq. (2), number of parts (k), transfer batch size (B k ), and part movement cost (C tk ) are set to one.

Table 3 Distance between facility locations
Full size table

According to Freund (1992), the 100*(1 − α)% confidence interval for difference between means of two populations is calculated as Eq.(36), where, n 1 and n 2 are sample size, \(\overline{{x_{1} }}\) and \(\overline{{x_{2} }}\) are sample means, \(\sigma_{1}^{2}\) and \(\sigma_{2}^{2}\) are sample variances, and \(z_{{{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}\) is standard normal Z value so that \(\Pr \left( { - z_{{{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \le Z \le z_{{{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right) = 1 - \alpha .\)

$$\left( {\overline{{x_{1} }} - \overline{{x_{2} }} } \right) - z_{{{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \sqrt {\frac{{\sigma_{1}^{2} }}{{n_{1} }} + \frac{{\sigma_{2}^{2} }}{{n_{2} }}} < \mu_{1} - \mu_{2} < \left( {\overline{{x_{1} }} - \overline{{x_{2} }} } \right) + z_{{{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \sqrt {\frac{{\sigma_{1}^{2} }}{{n_{1} }} + \frac{{\sigma_{2}^{2} }}{{n_{2} }}}$$
(36)
$$\overline{x} = \frac{{\sum\nolimits_{i = 1}^{n} x }}{n}$$
(37)
$$\sigma^{2} = \frac{1}{n - 1}\sum\limits_{i = 1}^{n} {\left( {x_{i} - \overline{x} } \right)}^{2}$$
(38)

After solving each test problem, the optimal value of total cost (objective function) is obtained as a sample of a population. Actually, two populations can be considered as follows. The first population includes optimal cost values obtained by the proposed hybrid algorithm and the second one is the population of optimal cost values obtained by the SA algorithm with a known initial solution. Using Eqs. (36)–(38) the sample means (\(\overline{{x_{\text{Hybrid}} }}\) and \(\overline{{x_{\text{SA}} }}\)) and sample variances (\(\sigma_{\text{Hybrid}}^{2}\) and \(\sigma_{\text{SA}}^{2}\)) of the optimal cost values along with the calculated 95% confidence interval for difference between means of the populations are shown in Table 4. According to the computational results, both of the lower and upper bounds of the confidence interval are negative, and thereby \(\mu_{\text{Hybrid}} < \mu_{\text{SA}}\). The average computation time elapsed for each problem is also displayed in Table 4. According to the results, the proposed hybrid algorithm has better performance than the SA algorithm from both the solution quality and computation time standpoints. Besides, this section indicates the capability of the proposed model and the hybrid algorithm to cope with the stochastic environment of facility layout problems.

Table 4 A comparison between the hybrid and SA algorithms
Full size table

Benchmark method

Since there is no historical data on the expectation, variance, and covariance of demands in each period, the proposed model is tested in a deterministic environment by comparing with previous approaches as benchmark. To this end, a 50% percentile level (p = 50%) equivalent of z p  = 0 is applied to the model. By doing so, the second term of the proposed model containing variance and covariance of part demands is ignored, thereby there is no need to data on variance and covariance of part demands in each period. In this case, demand of parts in each period, which is known in deterministic case, is regarded as the expectation of part demands in the proposed model. Data set used for testing the model are taken from Yaman et al. (1993). The problem includes nine machines and five periods. Data on machine sequence and part demand in different periods are given in Tables 5 and 6, respectively. Rectangular layout configuration is considered so that a location grid of 3 × 3 is used as facilities locations. Part movement cost, and batch size are set to ten and one, respectively.

Table 5 Data on machine sequence
Full size table
Table 6 Part demand in different periods
Full size table

Yaman et al. (1993)’s problem is applied to the proposed model. The proposed CS-SA hybrid algorithm is used to solve the model. To compare the performance of the proposed model with the previous approaches, which deal with the static environment, facility relocating cost is set to zero. Madhusudanan-Pillai et al. (2011) proposed a SA algorithm to solve their robust layout design model, which is termed MP-SA hereafter. Another heuristic method was also developed by Irappa and Madhusudanan (2008) to solve their model, which is denoted by I-M hereafter. The results of the proposed hybrid algorithm and the results of different approaches in literature are shown in Table 7. The findings contain the MHC of the optimal layout in each period and the total MHC over the entire planning horizon. On comparison, better performance of the proposed CS-SA hybrid algorithm is concluded so that it leads to 2.1% improvement with respect to the best previous approach (i.e. MP-SA). Besides, the approaches in literature except for the I-M and MP-SA methods, can be used only for problems having maximum nine machines, whereas the proposed approach including the dynamic model and the hybrid algorithm can be applied to any size of the problem. Finally, this section shows the capability of the proposed model and the hybrid algorithm to deal with the deterministic situation of facility layout problems.

Table 7 MHC of the proposed model and previous approaches
Full size table

Conclusion

In this paper, a novel hybrid CS-SA algorithm along with a new QAP-based mathematical model to design a dynamic facility layout was proposed to solve the SDFLP. Solving the proposed model leads to design of an optimal facility layout in each period of the multi-period time planning horizon. In the proposed algorithm, a population of randomly generated feasible initial solutions is improved using the CS algorithm. In fact, in the proposed hybrid algorihm, the SA algorithm starts with a population of good initial solutions rather than a single initial solution. The performance of the proposed model and the hybrid algorithm was evaluated using design of experiment (a large number of randomly generated test problems) and benchmark (data from the literature) methods with the following conclusions: (1) on the basis of computational results obtained by the design of experiment method, the proposed hybrid algorithm has outstanding performance in comparison with the SA algorithm starting with a single initial solution from both solution quality and computational time standpoints; (2) according to findings of benchmark method, better performance of the proposed CS-SA hybrid algorithm is concluded so that it leads to 2.1% improvement in total cost with respect to the best previous approach; (3) in spite of some approaches in literature, the proposed hybrid algorithm can be applied to any size of the problem; (4) in the proposed dynamic layout design model, the relative contribution of the expectation and variance of demands on the total cost can be controlled using a decision maker’s defined percentile p value; (5) in practice, the proposed model can be applied to both of the stochastic and the deterministic environments of manufacturing systems. Regarding the limitations of this research, since the proposed model has been developed based on QAP formulation, it can be applied only to layout problems having equal-sized facilities such as Raytheon Aircraft Company (Krishnan et al. 2006) and Vought Aerospace Company in Dallas, Texas (Groover 2008) as two real cases. Finally, the following works can be taken into consideration in the future researches:

  • To propose a more effective hybrid meta-heuristic approach by combining the SA algorithm with other intelligent approaches to improve the quality of the solution and the computational time.

  • To apply the population of initial solutions constructed by the CS, to other algorithms such as GA, TS, and PSO approaches.

  • To consider some constraints such as unequal-sized machines, adding and removing machines in different periods, closeness ratio, aisles, routing flexibility, and budget constraint for total cost.