Introduction

Green logistics has emerged recently and has attracted some researchers’ attention and has a great role in supply chain management in recent years. In the traditional logistics model, only economic objective is considered, but in green logistics, societal and environmental objectives are considered in addition to the economic objective. Integrating between vehicle routing problem (VRP) and green logistics developed a new field in logistics problem called Green Vehicle Routing Problem (GVRP). Lin et al. (2014) published a complete review on GVRP and provided a classification of GVRP. They categorize these problems into three branch lines including Green-VRP, Pollution Routing Problem and VRP in reverse logistics. They surveyed these problems completely and suggested research gaps. Implementation of environmentally sensitive logistic policy causes changing in transportation plans and causes decline in negative impacts on the environment. Some researchers like Bloemhof-Ruwaard et al. (1995) specified the relation and contributions of operational research methods to environmental management and addressed some reverse logistics in product recovery management and routing of wastes. Reverse logistics has received researchers’ attention in recent years. VRP in reverse logistics concentrate on the distribution aspects of reverse logistics. Most VRP in reverse logistics (VRPRL) deal with collection and recycling and conveying wastes and garbage or end of life goods to treatment facilities or disposal centers or both of them. Lin et al. (2014) considered four categories for reverse logistics in VRP: pickup with pricing, waste collection, end of life goods collection and simultaneous collection and distributions.

Waste collection problem is one of the most important applications of vehicle routing problems in real world and can integrate topics related to VRP with Green VRP. Waste collection management includes all activities related to collect, reuse, dispose and recycling of wastes. These processes are key activities in protecting environment and conserving resources. Using of vehicle routing models in waste collection dates back to Beltrami and Bodin (1974). Alumur and Kara (2007) proposed a new model for the hazardous waste location routing problem. The model objective functions were minimization of total cost and transportation risk. The model was applied in real world case study in central Anatolian region of turkey.

In recent years different kinds of VRP models are addressed in the literature and this problem has attracted very extensive attention of researchers for almost 50 years old. VRP is classified in NP-hard problems namely no exact algorithm is available for solving these problems in large-scaled problems (Toth and Vigo 2001). Various survey papers have been published to show the state-of-the-art in this topic. For instance Laporte (2009), Marinakis and Migdalas (2007), Potvin (2009) published review papers about vehicle routing problem. Multi-depot vehicle routing problem (MDVRP) which is kind of the VRP studied by Tillman (1969) for the first time. HO et al. (2008) proposed two hybrid genetic algorithms improved with some improvement heuristics for solving the MDVRP. Liu and Jiang (2012) proposed close and open mixed vehicle routing problem called COMVRP for the first time and they proposed new mathematical model for this problem and solve the problem by using memetic algorithm. Recently, Rabbani et al. (2016) used a rich VRP model to simulate the waste collection problem. They used analytical hierarchical process (AHP) to improve genetic algorithm (GA) for solving a proposed problem. The result showed the better performance of hybrid algorithm.

The design of distribution system is one of the critical decisions in management. For instance facility location problem (FLP) must be solved in a strategic level to specify locations of facilities, depots, warehouses, disposal and treatment facilities, etc., Also, vehicle routes must be built for servicing customer at operational level of decision making regarding customers’ demands. Location and routing problems are dependent and as studies shown in the literature, solving these problems separately leads to more cost than solving the two problems simultaneously. The location routing problem integrates two kinds of NP-hard problems. Classical location routing problem (LRP) consists of opening facilities in the potential locations for the facilities, assigning customers to these locations and determining vehicles routes. In this type of the problem objective function is minimization of the total cost including opening cost of facilities and the total cost of routes. Demands of customers assigned to depot must not exceed from capacity of depot. Also, each route starts from one depot and ends in the same one and each customer is served only by one vehicle. As shown in two comprehensive survey on the LRP number of articles devoted to this type of problem has grown rapidly (Nagy and Salhi 2007; Prodhon and Prins 2014). Salhi and Rand (1989) showed that solving the location and routing problem separately leads to suboptimal solution so these two problems must be considered simultaneously. Tavakkoli-Moghaddam et al. (2010) proposed a new integrated mathematical model for bi-objective multi-depot location routing problem. They solved this problem by means of multi-objective scatter search (MOSS) algorithm to obtain the Pareto frontier and the operation of this algorithm compare with the elite tabu search. Also, Wu et al. (2002) considered multi depot location routing problem which the location of the depots must be chosen from potential locations and should be specified the routes to serve the customers from depots. Hashemi-Doulabi and Seifi (2013) addressed the location arc routing problem with uncapacitated depots. They represented a mixed integer programming and used simulated annealing (SA). Economics cost is usually considered in LRP, but in new spectrum of optimization problems related to LRP societal and environmental objectives are considered such as the problems related to location of obnoxious facilities and waste disposal centers (Cappanera et al. 2003; Xie et al. 2012) Barreto et al. (2007) used clustering analysis in capacitated location routing problem. The fleet of vehicles is supposed to be homogeneous and vehicles can carry a single type of products. Several hierarchical and non-hierarchical clustering techniques used and new proximity function for clustering of customers proposed in their paper. In addition to the addressing a facility location, the model extended by Jabbarzadeh et al. (2016) is able to determine the required processing technology at each transfer station. Minimization of costs, energy consumptions and greenhouse gas emissions are objective functions of the paper. In another study, Eiselt and Marianov (2014) proposed a bi-objective mixed-integer linear programming model to locate disposal and transfer stations and determine the size of each facility. Minimization of costs and pollution was investigated as objective functions in their model. Also, these authors studied the issue of locating solid waste management facilities involved communal waste collection stations by the aim of minimization of the total distance travelled (Eiselt and Marianov 2015).

As aforementioned, facility location and also routing problems have a NP-hard nature. For this reason, metaheuristic algorithms can be applied for tackling these problems. GA is one of the most popular metaheuristic algorithm in solving a combinatorial optimization problems (Rabbani et al. 2016). Non dominated genetic algorithm (NSGA-II) is an extension for the GA which is used for solving the multi objective optimization problems and is proposed by Deb et al. (2002). Bhattacharya (2011) applied NSGA-II for solving a vertex covering obnoxious facility location model on a plane was designed with a combination of three objective functions. Bhattacharya and Bandyopadhyay (2010) focused on the facility location problem with two conflicting objectives including cost of each echelon and cost of whole supply chain. They solved the problem formulated in mixed nonlinear programming by a NSGA-II. Martínez-Salazar et al. (2014) introduced a new version of LRP and called it transportation location routing problem (TLRP). This problem combined transportation problem with LRP and NSGA-II was used to solve the bi-objective problem.

In this paper, we consider waste collection problem that location of depots and treatment facilities must be selected from discrete potential locations. A new integrated mathematical model for a bi-objective waste collection problem with multi-depots and several treatment facilities is presented. Mixed open and close routes are addressed in this work. In addition, fleet of vehicles are multi-compartment and each type of waste must be treated in a treatment facility with compatible technology. Capacity of vehicles and depots are limited and servicing to some customers is delegated to contractor, so two types of fleet are available: internal and external ones. Also the distance and times of routes are limited. This paper considers economic and societal objectives simultaneously and uses multi objective meta-heuristic and decomposition methods to solve the problems and the results are compared with each other. The proposed model could be applicable for the waste collection corporation which has own fleet of vehicles, but designates a part of services to contractor or external vehicles. Also, establishing a technology and decision about which technology might be appropriate for treatment centers are critical and strategic decision which should be made in the process of operations management in treatment facilities. Moreover, some regulations of governments or pressure from non-government organizations oblige corporation to take environmental and social issues into considerations. This fact motivates us to consider a bi-objective problem to reduce unfavorable effects of wastes on the society.

The paper is organized as follow: In “Problem statement”, we briefly describe concepts of multi objective optimization. The mathematical model also is represented in “Problem statement”. Proposed approach to solve the problem is considered in “Methodology”. Experimental results and comparisons of the methods are given in “Experimental results”. Finally, we represent conclusion and future research parts in “Conclusion and future research”.

Problem statement

Multi-objective optimization

Single objective optimization problems aim to find the optimal or near optimal solution(s). In this type of problems, comparison of the solutions existing in the solution area is simple; because only one objective value is available and sorting of solutions regarding this objective functions is performed. For example, in minimization problem, if f(x) < f(y), we can conclude that solution x is better than solution y. However, in multi objective problems, it is difficult to find a single solution which optimizes all objective functions, simultaneously. In multi-objective problems, objective functions of each solution is considered as a vector. Therefore, multi-objective optimization is called multi criteria optimization or vector optimization. A feasible solution which satisfies all constraints and includes decision variables. These objective function are usually in conflict with each other. So the term of optimization means that finding the solution which can satisfy all constraints and gives acceptable values for all objective functions. We can define it as a mathematical formulation as follows:

If x = [x 1, x 2, x 3 ,…, x N ]T is the vector of decision variables, we want to find the vector x * = [x *1 , x *2 , x *3 ,…, x * N ]T which satisfies all constraints and optimizes the vector of objective function:

$$\begin{aligned} g_{i} (x) \ge 0 \quad i = 1,2,3, \ldots ,p \, \hfill \\ h_{j} (x) = 0 \quad j = 1,2,3, \ldots ,q \, \hfill \\ \end{aligned}$$
$$F = [f_{1} (x),f_{2} (x),f_{3} (x), \ldots ,f_{m} (x)]^{T}$$

In other words, we intend to find the solutions which satisfy aforementioned constraints and yield to the optimum values of all objective functions. However, finding the solution which optimizes all objectives and satisfies all constraints is usually impossible; hence, we define the concept of dominant solutions. Let us consider a general multi objective maximization problem with n decision variable and m objectives (m > 1):

$${\text{maximize }}f(x) = [f_{1} (x),f_{2} (x), \ldots ,f_{m} (x)]$$
$${\text{where }}x \in R^{n} \, and \, f(x) \in R^{m}$$

We define that solution x dominates the solution y for maximization problem if:

$$f_{i} (x) \ge f_{i} (y) \quad \forall i \in \left\{ {1,2, \ldots ,m} \right\}$$
$$f_{i} \left( x \right) > f_{i} \left( y \right) \quad \exists i \in \left\{ {1,2, \ldots ,m} \right\}$$

If a solution is available so that no solution dominates it, this solution is called non-dominated solution. The solutions that are not dominated by any other solutions in the feasible area are called Pareto optimal. Their corresponding images in the objective space are called Pareto frontier.

Problem description

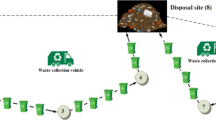
The problem considered in this paper can be described as follows: Expected demands and locations of customers are deterministic and known. Also, the potential locations for depots and treatment facilities are given (i.e., the set of depots and treatment facilities must be chosen from these potential locations). Two types of fleet are considered in this paper (Internal and external fleets). Vehicle belonging to internal fleet should come back to depot which vehicles exit from, but external fleets are free after unloading the wastes in last treatment facility. Therefore, the routes are mixed open and close. Vehicles are homogeneous and have maximum capacity constraint. We also consider maximum allowable time for servicing customers and maximum allowable route length, simultaneously. Vehicle starts its route from depot and collects wastes from customers’ locations. After finishing collection of wastes, vehicle moves to treatment facilities. Note that vehicles are multi-compartment and have specific parts to each type of waste. Each waste type should be treated in treatment facility that has compatible technology to treat this type of waste. There is fixed cost associated with opening a treatment facility and depot at each potential location. Distribution cost associated with routes including the fixed cost of vehicles for external ones and variable cost that is proportional to the total time traveled by the vehicle. We want to determine location of depots and treatment centers and vehicle routes in this problem. The objectives function includes minimization of total cost and maximization of distance between opened treatment facilities and customers. The example of this problem is shown in Fig. 1. To illustrate the problem addressed in this paper, a mathematical formulation is provided. The mathematical model aims to simplify understanding of objectives and constraints of the problem. It should be mentioned that the proposed model can be solved by means of some commercial software packages such as GAMS, Lingo, and CPLEX to find exact solutions. However, regarding NP-hard nature of the problem, applying metaheuristic algorithms to tackle the problem especially in large scale problems is rational.

Fig. 1
figure 1

The schematic figure for open and close routes

Full size image

Problem assumptions

1.:

The demand of each customer and its location are deterministic and known

2.:

Each customer is served by only one vehicle

3.:

Internal vehicles should return to the depot, but the external ones should not return to depot

4.:

Capacity of vehicles and depots are limited

5.:

Vehicles are homogeneous and vehicles are constrained in time and distance

6.:

There are some types of waste

7.:

Each type of waste should be treated in compatible treatment technology

8.:

Only external vehicles have fixed cost for starting their routes

9.:

Vehicles are multi compartment and have limited capacity for each type of waste.

Notations

Sets:

D :

{d, d′|d, d′ = 1, 2, …, M} Set of potential depots

C :

{c, c′|c, c′ = 1, 2, …, N} Set of customers

F :

{f|f = 1, 2,…, Y} Set of potential treatment facilities

S :

{s|s = 0, 1} Fleets type (internal or external)

W :

{w|w = 1, 2,…, O} Set of wastes type and corresponding treatment technology

K :

{k|k = 1, 2,…, T} Set of vehicles

R :

{r|r = 1, 2,…, M + N} Set of depots and customers nodes

P :

{p|p = 1, 2,…, N + Y} Set of customers and potential treatment facilities

A :

\(\{ i,j|i,j = 1,2, \ldots , M + N + Y\}\) Set of all nodes

Parameters:

d ij :

Distance between node i and node j

t ij :

Travel time between node i and node j

f 1 :

Fixed cost of external fleet

v k :

Variable cost of vehicle k per unit of time

q cw :

Demand of customer c for treatment of waste type w

τ cwsk :

Loading time per unit of waste w in customer node c by means of vehicle k of fleet s

cap kw :

Maximum vehicle k capacity for load waste type w

E :

Maximum allowable route length

H :

Maximum allowable time to servicing customers in each route

Ω d :

Maximum capacity of depot d

π fw :

Fixed cost of opening treatment facility with technology w in potential location f

π′ d :

Fixed cost of opening depot in potential location d

M :

Big value

Decision variables:

x ijsk :

If vehicle k of fleet s travels directly from node i to node j, x ijsk  = 1; otherwise = 0

z csk :

If vehicle k of fleet s is allocated to customer c, z csk  = 1; otherwise = 0

y fw :

If treatment facility with technology w is opened in potential location f, y fw  = 1; otherwise = 0

o d :

If depot is opened in potential location d, o d  = 1; otherwise = 0

U rskw :

Continuous variable that represents the load of compartment w vehicle k of fleet s just after leaving node r

Mathematical models

$$\begin{aligned} {\text{minimize }}\sum\limits_{k \in K} {\sum\limits_{c \in C} {\sum\limits_{d \in D} {f_{1} \, x_{dc1k} } } } \, + \, \sum\limits_{s \in S} {\sum\limits_{k \in K} {\sum\limits_{j \in A} {\sum\limits_{i \in A} {v_{k} \, t_{ij} x_{ijsk} } } } } \hfill \\ - \sum\limits_{k \in K} {\sum\limits_{d \in D} {\sum\limits_{f \in F} {v \, t_{fd} x_{fd1k} } } } \, + \, \sum\limits_{f \in F} {\sum\limits_{w \in W} {\pi_{fw} y_{fw} } } \, + \, \sum\limits_{d \in D} {\pi_{d}^{'} } o_{d} \hfill \\ \end{aligned}$$
(1)
$${\text{maximize }}\mathop {\hbox{min} }\limits_{\begin{subarray}{l} c \in C \\ f \in F \\ w \in W \end{subarray} } (d_{cf} y_{fw} )$$
(2)
$$\sum _{s \in S} \sum _{k \in K} \sum _{r \in R} x_{rcsk} = 1\quad \forall c \in C$$
(3)
$$\mathop \sum \limits_{i \in A} x_{ijsk} = \mathop \sum \limits_{i \in A} x_{jisk} \quad \forall j \in A, s \in S, k \in K$$
(4)
$$\mathop \sum \limits_{d \in D} \mathop \sum \limits_{d' \in D} x_{dd'sk} = 0 \quad \forall s \in S, k \in K$$
(5)
$$\sum _{r \in R} x_{rcsk} = z_{csk }\quad \forall c \in C, s \in S, k \in K$$
(6)
$$\sum _{r \in R} \sum _{c \in C} t_{rc} x_{rcsk} + \sum _{w \in W} \sum _{c \in C} \tau_{cwsk} q_{cw} z_{csk} \le \, H \forall s \in S, k \in K$$
(7)
$$\sum _{s \in S} \sum _{k \in K} \sum _{c \in C} x_{dcsk} \le \varOmega_{d} o_{d } \quad \forall d \in D$$
(8)
$$\begin{aligned} U_{dskw} = 0\quad \forall d \in D, s \in S, k \in K, \hfill \\ \quad \quad \quad \quad w \in W \hfill \\ \end{aligned}$$
(9)
$$\begin{aligned} U_{cskw} + q_{c'w} - M\left( {1 - x_{cc'sk} } \right) \le U_{c'skw} \quad \forall c,c' \in C, s \in S, k \in K, \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; w \in W \hfill \\ \end{aligned}$$
(10)
$$q_{cw} \le \mathop \sum \limits_{s \in S} \mathop \sum \limits_{k \in K} U_{cskw} \le \mathop \sum \limits_{s \in S} \mathop \sum \limits_{k \in K} \mathop \sum \limits_{r \in R} x_{rcsk} cap_{kw} \quad \forall c \in C, w \in W$$
(11)
$$\sum _{i \in A} \sum _{j \in A} d_{ij} x_{ijsk} \le E\quad \forall s \in S, k \in K$$
(12)
$$\mathop \sum \limits_{c \in C} q_{cw} z_{csk} \le cap_{kw} \quad \forall w \in W, k \in K, s \in S$$
(13)
$$\sum _{s \in S} \sum _{k \in K} \sum _{f \in F} \sum _{d \in D} x_{dfsk} = 0$$
(14)
$$\mathop \sum \limits_{s \in S} \mathop \sum \limits_{k \in K} \mathop \sum \limits_{d \in D} \mathop \sum \limits_{c \in C} x_{cdsk} = 0$$
(15)
$$\mathop \sum \limits_{s \in S} \mathop \sum \limits_{k \in K} \mathop \sum \limits_{c \in C} \mathop \sum \limits_{d \in D} x_{dcsk} = \mathop \sum \limits_{s \in S} \mathop \sum \limits_{k \in K} \mathop \sum \limits_{p \in P} x_{pfsk} \quad \forall f \in F$$
(16)
$$\sum _{f \in F} y_{fw} = 1\quad \forall f \in F$$
(17)
$$\sum _{w \in W} y_{fw} \le 1$$
(18)
$$\begin{aligned} x_{ijsk} = \left\{ {0, 1} \right\}\quad \forall i,j \in A,s \in S, \hfill \\ \quad \quad \quad \quad \quad k \in K \hfill \\ \end{aligned}$$
(19)
$$z_{csk} = \left\{ {0, 1} \right\}\quad \forall c \in C, s \in S, k \in K$$
(20)
$$y_{fw} = \left\{ {0, 1} \right\}\quad \forall f \in F, w \in W$$
(21)
$$o_{d} = \left\{ {0, 1} \right\}\quad \forall d \in D$$
(22)
$$\begin{aligned} U_{rskw} \ge 0\quad \forall r \in R, s \in S , k \in K, \hfill \\ \quad \quad \quad \quad w \in W \hfill \\ \end{aligned}$$
(23)

Objective function (1) corresponds to economic cost. In term one of objective function fixed cost of external vehicles is considered. In second term variable cost of transportation is considered, but we should lessen cost of returning external vehicles that we take into account in term 2. In term 4 we consider fixed cost of opening treatment facilities in potential locations and in term 5 cost of opening depots is considered. In objective function (2) societal rejection of establishing of treatment facilities is addressed. Treatment facility is obnoxious facility and should be away from urban area. In this function, we want to make far treatment facilities from customers’ location. Constraints (3) and (4) guarantee that each customer is assigned to only one route. Constraints (5) prohibit travelling between depots. Constraints (6) determine the relationship between two types of decision variables. Constraints (7) satisfy time limitation to serve the customers in each route. Numbers of vehicles that depart from each depot should not trespass from depot’s capacity. Constraints (8) consider the capacity of each depot that is opened in potential location. The next three sets of constraints (9)–(11) are lifted Miller–Tucker–Zemlin (MTZ) sub tour elimination constraints (Kara et al. 2004). In constraint (10), parameter M is set equal to summation of all customers’ demand. Constraints (12) guarantee that each route’s length do not trespass from maximum allowable route length. Constraints (13) consider the capacity of vehicles in each route. Constraint (14) bans moving from depots to treatment facilities directly and constraints (15) bans moving from customers to depots before crossing treatment facilities. Constraints (16) satisfy that all vehicles that depart from depots must visit all treatment facilities established in potential locations. Constraints (17) represent that only one treatment facility for each type of waste must be opened. Constraints (18) guarantee that treatment facilities do not overlap with each other. Constraints (19)-(23) specify the ranges of the variables.

Methodology

In the early works in the literature of location routing problem, the most frequent approach for tackling the LRP was decomposition of problem into two separate problems.(i.e. location first and routing second or conversely). Because this manner doesn’t consider the trade-off between these two problems, solutions obtained with this strategy are not optimal or reasonable solutions. ‘‘The waste location routing problem can be seen as NP-hard by reducing it to uncapacitated facility location problem’’ (Alumur and Kara 2007). Hence, meta-heuristic algorithms are used to solve the integrated problem iteratively. Some assumptions such as number of treatment facilities are needed to be considered in solving the problem. Number of treatment facilities are already known and equal to the number of waste types (We suppose that for each type of waste one compatible technology is available) and the location of these facilities should be chosen from potential locations. Note that depots do not impact on societal objective because of only treatment facilities are undesirable facility and have bad effect on human life. The algorithm used in this paper (NSGA-II) are population based algorithm, so the algorithms need to constructive algorithm which generates initial population of solutions. The rest of the methodology section is formed from description about solution representation, constructive method and metaheuristic algorithms used in this paper.

Solution representation

The manner in which the solutions of the problem are coded has a significant impact on the quality of the solutions and computational time. The initial structure of the solutions in both algorithms is made up from two strings of real numbers between 0 and 1. These structures in the context of NSGA-II is called chromosome. The first string consists of N + M − 1 real numbers generated randomly. Where N is the number of customers and M is the number of potential locations for depots. Figure 2 demonstrates that how the real numbers in the string are transformed to the permutation of integer numbers between 1 to \(N + M - 1\).

Fig. 2
figure 2

Example of chromosome of the solutions

Full size image

One integer number is assigned for each real number consecutively. After this, the real numbers are sorted in descending order and the assigned numbers are moved with corresponding real numbers. The result of this work is a random permutation of integer numbers.

This permutation specifies the assignment of customers to the depots and also determines which depot will be opened for servicing customers. Numbers between 1 and N represents customers and the numbers that are bigger than N represents depots. The numbers in the range of [N + 1, N + M − 1] have a role of delimiter. Customers till fist delimiter are assigned to the first depot. Customers between first delimiter and second delimiter are assigned to the second depot and so on. If no customer is available between two delimiter this means that no customer is assigned to the corresponding depot. Figure 3 is the example that shows the manner in which the customers are assigned to the depot. Numbers 8 and 9 represents delimiters, so customers 5, 1, and 7 are assigned to the first depot. Customers 4 and 6 are assigned to depot 2 and customers 2 and 3 are assigned to depot 3.

Fig. 3
figure 3

Example of customers’ assignment to depots

Full size image

The second string is similar to the first one. This string consists of Y real numbers (Y is the number of potential location for treatment facilities) and the manner in which the permutation is generated is similar to the descriptions mentioned previously. After generation of the permutation, the first O number (O is the number of treatment facilities should be established) are selected for establishing treatment facilities.

The next step is generation of the routes with regard to assignment of customers to depots and opened treatment facilities. For each opened depot and customers assigned to it, the customers form routes with respect to capacity of vehicles for each type of the wastes. Customers are assigned to vehicle till their demands exceed from capacity of the vehicle. Structure of each route after generation is demonstrated in Fig 4. The chromosome of each route in the solution area consists of several parts and each part specifies particular attributes of the solution. First part specifies that route starts from which depot. Second part shows that the route is close or open means that the vehicle assigned to this route is external or internal. Number 0 represents internal fleet and number 1 represents external one. For this part one uniform random number is generated in the range of (0–1). If the generated number is bigger than 0.5, the vehicle is belonged to the external fleet and if the generated number is lower than 0.5, the vehicle is belonged to the internal fleet. Third part specifies customers serviced in this route. Note that cumulative demands of customers must not exceed the capacity of vehicle. Also, the time and distance constraints and the capacity constraint for depot must be considered. We use penalty in both objective functions for trespassing from these limitation in each route. Fourth part includes treatment facilities and shows facilities order in the route. The random permutation of opened facilities is placed in this section. Fifth part marked with dash line is depended on the route. If the route is close this part is equal to part one and if the route is open this part should be empty. These route structures combine with each other and make the solution structure. (Because the dimension of each route may be different in the solution structure we use cell array structure in Matlab software to code the solutions).

Fig. 4
figure 4

Example for a structure of Solutions

Full size image

Initialization

NSGA-II is a population based algorithm and some solutions should be constructed for initialization. Clustering approach is used for construction of initial population of solutions. In the first step, we should cluster customers according the proximity coefficient, customers demand for each type of waste, and vehicles capacity. Recognizing clusters of customers can be a good start to find efficient solutions for this problem. Cluster analysis has several methodologies that can be used in heuristic manner for solving this type of problems.

Several metrics are proposed for calculating the proximity between two points, however, the most popular and most common proximity measure between the two points is an Euclidean distance that determine the proximity between the points I = (x i , y i ) and J = (x j , y j ) as follows:

$$d(I,J) = \sqrt {(x_{i} - x_{j} )^{2} + (y_{i} - y_{j} )^{2} }$$
(24)

Also several measures of proximity between two groups of points are available (e.g. single linkage, group average, centroid, ward and saving measures) (Barreto et al. 2007). We use centroid proximity measure for clustering customers. An important element on the centroid proximity measure is the centroid or gravity center of groups. Centroid of group A which we show by mA is defined as:

$$m_{A} = \left( {\frac{{\sum\limits_{i \in A} {x_{i} } }}{\left| A \right|},\frac{{\sum\limits_{i \in A} {y_{i} } }}{\left| A \right|}} \right)$$
(25)

We start with groups that consist on only one customer. In other words, each customer is considered as a group in the starting point of the method. Then, one node of customers is considered and another customer is added to this group which has a biggest proximity coefficient whit the first selected customer. In merging of groups with each other and selection of groups that have a highest value of proximity coefficient, we consider the centroid of groups and calculate the Euclidean distance between the centroid of two groups. Graphical and analytical representation of this proximity measure is shown in Fig 5. Note that in adding the customers to group, the capacity of vehicles must be considered in addition to proximity coefficient. Customers are added to a group until they do not exceed the capacity of the vehicle. If adding a customer leads to trespassing from vehicle capacity, the next customer with the highest similarity are added to the group.

Fig. 5
figure 5

Proximity coefficient between two groups

Full size image

After clustering of customers, the next step is the assignment of the clusters to the depots. For each cluster of customers, the depot that has a highest similarity coefficient with the cluster is selected. At this point, the clusters and assigned depots are determined. For the next step, this solution should be transformed into meaningful solution to the algorithm for applying algorithm’s operator and construction of next generations. As mentioned before, each solution is represented with two strings of real numbers in the range of (0–1). The obtained clusters are transformed into first string and the second string is generated randomly.

NSGA-II for solving the problem

Genetic algorithm proposed by John Holland (1975) is one of the most popular and applicable evolutionary metaheuristic to solve problems which are hard to find exact and optimal solutions. NSGA-II is an extension for the genetic algorithm and is used for solving the multi objective problems and is proposed by Deb et al. (2002). Algorithm starts with the initialization step. In this step, initial population is generated according to the section mentioned previously. After this step obtained solutions are improved each iteration by means of crossover and mutation operators. The manner in which fitness function is calculated is critical and important factor in evolutionary algorithms. In the proposed NSGA-II, objective functions are considered as a fitness functions without any change. The steps of algorithms are as follow (Amiri and Khajeh, 2015):

Step 1 Initial population with the size of npop = 150 is generated with the respect to clustering approach for grouping customers.

Step 2 According to the concept of dominance the solutions are ranked into rank one, two and etc. Rank one is better than rank two with regard to dominance concept and rank two is better than rank three and so on.

Step 3 Crowding distance is calculated for the solutions that are in the same rank by means of crowding distance operator.

Step 4 In this step, the solutions are sorted according to rank of each solution and crowding distance number. Rank of the solution is the first priority for sorting and crowding distance is the second priority (i.e. the solution which has better rank number is prior but if two solutions have the same rank number, the solution that has bigger crowding distance is prior.)

Step 5 Solutions are selected for crossover operator by means of roulette wheel operator and randomly selection for mutation.

Step 6 Crossover and mutation operators are performed to improve the solutions.

Step 7 The offsprings obtained from crossover and mutation operators are merged with together to produce a new generation.

Step 8 In this step the rank of merged solutions are specified and the crowding distance is calculated.

Step 9 With regarding to the values obtained in the previous step the solutions are sorted.

Step 10 Population is truncated to reach the number of desirable population size (npop).

Step 11 In this step rank 1 of new generation is selected and is depicted as a Pareto front.

Step 12 The stopping criterion considered to be the maximum number of iterations, i.e. MaxIt = 100, is checked. If it is reached, the algorithm stops, otherwise, steps 2–12 are repeated.

Crossover and mutation operators

The performance of NSGA-II algorithm is highly dependent on crossover and mutation operators. By these operators, we can search in the solution area and explore new solutions and exploit good solutions. In the genetic algorithm literature, there are vary crossover and mutation operators that can be used according to type of problem.

First, we select parents to perform crossover operation by roulette wheel operators. First parent is selected by applying roulette wheel operator on first objective function and the second parent is selected with respect to second objective functions. After selection of parents, we produce one integer random number between 1 and 3. In case 1, crossover operator is applied on first string. In case 2 only second string and in case 3 both of them are selected to perform crossover operator. Mathematical formulation for applying crossover operator is as follows:

$$\left\{ {\begin{array}{*{20}c} {y_{i}^{1} = \alpha x_{i}^{1} + (1 - \alpha )x_{i}^{2} } \\ {y_{i}^{2} = \alpha x_{i}^{2} + (1 - \alpha )x_{i}^{1} } \\ \end{array} } \right.\quad 0 < \alpha < 1$$
(26)

where y 1 i and y 2 i are first offspring and second offspring’s i-th component in the string. x 1 i and x 2 i are first parent and second parent’s i-th component. Also α is the random real number between 0 and 1.

Also we use several mutation operators such as reverse, insertion, and swap mutation operators for exploration new solutions. In reverse mutation, two genes are selected randomly and the genes position between two selected genes are reversed. In insertion, two genes are selected randomly and the second one is inserted after the first one. Swap mutation selects two genes in chromosome randomly and swaps them to generate new solutions.

Experimental results

The performance of a hybrid NSGA-II proposed in this paper is compared with decomposition methods such as weighted sum, goal programming, and goal attainment. The algorithms are coded in MATLAB R2013a and executed on Intel Core i5 2.27 GHz personal computer with 4 GB RAM. The brief discussion about decomposition algorithms used in this paper is presented in the next section.

Decomposition methods

In these methods the bi-objective problem is transformed into a single objective problem which is easier to solve. Since, in bi-objective problems solution area is not ordered, we cannot easily sort solutions. These methods are applied to obtain Pareto solutions.

Weighted sum algorithm (WS)

In this method, we transform a bi-objective problem to a single objective including weighted summation of the two objective functions. The transformation of objective function is shown as follows:

$$\begin{aligned} \hbox{min} \, f_{i} (x) \quad \forall i \in \left\{ {1,2, \ldots ,n} \right\} \to \\ \hbox{min} \, f_{ws} (x) = \sum\limits_{i = 1}^{n} {w_{i} f_{i} (x)} \, w_{i} \ge 0 \hfill \\ \end{aligned}$$
(27)

A new variable (Z) is considered as the weighted summation of two objective functions. We change all w i in each iteration and discover minimum value for Z. For the convenience is solving the problem the objective function two is transformed into minimization multiplied by minus one. Since the problem is classified as a NP-Hard problems, so we use genetic algorithm for optimization of Z. The algorithm is repeated for several sets of w i and we record all obtained solution for each set of w i . Finally, the recorded solutions are compared with other and non-dominated solutions from these solutions are introduced as a Pareto solutions. Note that because of the objective functions scales are different with each other, we normalize the objective functions as follows:

$$\hbox{min} \, \sum\limits_{i = 1}^{n} {w_{i} \overline{{f_{i} }} (x)} ,{\text{ where}}\;\;\overline{{f_{i} }} (x) = \frac{{f_{i} (x) - f_{i}^{\hbox{min} } }}{{f_{i}^{\hbox{max} } - f_{i}^{\hbox{min} } }}$$
(28)

where f max i and f min i are defined as maximum and minimum values of dimension i of objective function.

Goal programming method

In this algorithm we want to decrease the distance of objective functions from ideal point. This distance can be defined as several ways. Ideal point is obtained from experts or by solving each objective function separately and finding best solution for each objective function without consideration of other objectives. In this paper, we consider each objective function separately and for finding good ideal point, genetic algorithm is used. After finding ideal point, the objective function is transformed to single objective function that decreases the distance between objective function and ideal point (Moradgholi et al. 2016). We define T = (t 1, t 2,…, t n ) for ideal point. P-norm distance is defined as follow:

$$\left\| x \right\|_{p} = \sqrt[p]{{\sum\limits_{i = 1}^{n} {\left| {x_{i} } \right|}^{p} }} \quad x \in R^{n}$$
(29)

In goal programming approach, we use 1-norm distance (city-block distance) to evaluate distance between objective function and ideal point. So, bi-objective problem is transformed into single objective problem as follow:

$$\hbox{min} \, \sum\limits_{i = 1}^{n} {w_{i} \left| {f_{i} (x) - t_{i} } \right|}$$
(30)

We solve the problem for each set of w i and find optimal or near optimal solution with genetic algorithm. After finishing iterations we find non-dominated solutions from obtained solutions and provide Pareto-front.

Goal attainment method

All steps for this method is same as the goal programming method, but in goal attainment method the distance between objective functions and ideal point (target point) is calculated in infinity norm distance. (‖x‖∞ = max {x i } i ∊ {1, 2,…, n}), hence the objective function is transformed into single objective as follows:

$$\hbox{min} \left\| {f - T} \right\|_{\infty ,w} = \hbox{max} \, w_{i} \left| {f_{i} - t_{i} } \right| \, i = \left\{ {1,2, \ldots ,n} \right\}$$
(31)

We solve the problem for each set of w i and we find optimal or near optimal solutions. After finishing all iterations, we specify non-dominated solutions and provide Pareto-front.

Small and medium-sized problems

Test problems

First experiment is carried out for small and medium sized problems. 10 sample problems are generated according to Tables 1, 2. The proposed NSGA-II is applied to solve these test problems and the performance of proposed algorithm is compared with solutions obtained with decomposition methods. Several comparison metrics is applied in this paper and is introduced in next section. We run each test problem 15 times and the average values are shown in Tables 3, 4.

Table 1 Problem sets for small-size problems
Full size table
Table 2 Test problem generation
Full size table
Table 3 Computational results for small and medium sized problems
Full size table
Table 4 Average Computational times (in seconds)
Full size table

Comparison metrics

To validate the reliability of the proposed algorithm and to compare these algorithms with each other 4 comparison metrics are applied.

  1. 1.

    Number of Pareto solutions (NPS). The number of non-dominated solutions that each algorithm can find.

  2. 2.

    Spacing metrics (SM1). This metric gives us information about the uniformity of the spread of the solutions obtained by means of each algorithm. This metrics are calculated as follows:

    $$SM1 = \sqrt {\frac{1}{N - 1} \times \sum\limits_{i = 1}^{n} {(d_{i} - \overline{d} } } )^{2}$$
    (32)

    where d i is the Euclidean distance between solutions i and the closest solution to it in the Pareto sets of solutions. \(\overline{d}\) is the average value of all d i .

  3. 3.

    Spacing metrics (SM2). We use another spacing metric in addition to previous metric. This spacing metric is introduced by means of Schott (1995). The purpose of this metric is to measure how evenly the points in the approximation set are distributed in the objective space.

    $$SM2 = \sqrt {\frac{1}{n - 1} \times \sum {(d_{i} - \overline{d} )^{2} } }$$
    (33)
    $$d_{i} = \min_{j} (\left| {f_{1}^{i} (\overrightarrow {x} ) - f_{1}^{j} (\overrightarrow {x} )} \right| + \left| {f_{2}^{i} (\overrightarrow {x} ) - f_{2}^{j} (\overrightarrow {x} )} \right|),i,j = 1,2, \ldots ,n$$
    (34)

    and \(\overline{d}\) is the mean value of all d i .

  4. 4.

    Diversification metrics (DM). This metric specifies the spread of solution set and calculated as follows:

    $$DM = \sqrt {\sum\limits_{i = 1}^{n} {\hbox{max} (\left\| {x_{t}^{i} - y_{t}^{i} } \right\|)} }$$
    (35)

    where max (‖x i t  − y i t ‖) is the Euclidean distance between the non-dominated solutions x t  i and y t i .

Algorithms assumptions

For tuning the parameters of algorithms, extensive experiments is conducted with different sets of parameters with respect to Taguchi design. The following set is found to be effective in terms of solution quality and diversity level proposed by Minitab software.

  1. 1.

    NSGA-II assumptions

    • The algorithm is terminated after 100 iterations.

    • Number of population size is 150.

    • Crossover coefficient is set 0.8 and mutation coefficient is set 0.5.

  2. 2.

    Decomposition methods assumptions

    • Number of iterations for weighted sum algorithm is 100.

    • In goal programming and goal attainment methods, number of genetic algorithms iterations for finding the ideal point is 50.

    • Number of iterations for goal attainment and goal programming method is 100.

Comparative results

The proposed NSGA-II is applied to test problems and average results are shown in Table 3. All results is compared with decomposition methods including weighted sum, goal programming and goal attainment. Table 3 lists the average value of experiment results and the performance of all algorithms is compared with each other. Also average computational times are shown in Table 4. Table 3 shows that the proposed hybrid NSGA-II is superior in each test problem regarding to comparison metrics. Also, we can find out that the computational time is dependent on number of customers, depots, number of treatment facilities’ location and number of wastes types especially numbers of customers locations. The performance of algorithm and the figure of Pareto-solution for initial population and final solution in test problem number 9 are demonstrated in Figs. 6, 7 respectively.

Fig. 6
figure 6

Initial Pareto-front in solution area for problem 9

Full size image
Fig. 7
figure 7

Final Pareto-front in solution area for problem 9

Full size image

After consideration of obtained results and performance of algorithms to solve the problem we can result such as follows:

  • An average value of number of Pareto solutions (NPS) is greater for NSGA-II in all test problems.

  • Solutions obtained by NSGA-II are distributed more uniformly in comparison with decomposition methods. Both spacing metrics for NSGA-II are incredibly smaller than decomposition methods.

  • The average values for diversification metrics in NSGA-II are greater than decomposition methods in all test problems.

  • Table 4 shows the average computational times and proposed NSGA-II consumes more computational times than decomposition methods. Since NSGA-II search more regions of solutions space, this higher computational time is rational.

Large sized problems

Test problems

Another experiment is constructed in large scaled problems. To implement desirable test problems, 10 test problems are generated according to Table 5. Test problems attributes are same as small-sized test problems as mentioned in Table 2.

Table 5 Problem sets for large-sized problems
Full size table

Comparisons metrics

The comparison metrics for large-sized and small-sized problems are the same and we use number of Pareto solutions (NPS),two spacing metrics (SM1,SM2) and diversification metric (DM) for comparison of algorithms.

Algorithms assumptions

  1. 1.

    NSGA-II parameters

    • The algorithm is terminated after 50 iterations.

    • Number of population size is 100.

    • Crossover coefficient is set 0.5 and mutation coefficient is set 0.3.

  2. 2.

    Decomposition methods parameters

    • Number of iteration for weighted sum algorithm is 50.

    • In goal programming and goal attainment methods number of genetic algorithms iteration for finding the ideal point is 50.

    • Goal programming and goal attainment methods are terminated after 50 iterations.

Comparative results

Table 6 shows that proposed hybrid NSGA-II performed better than decomposition methods in all test problem, but the number of Pareto solutions (NPS) is not very greater than decomposition methods. Also Table 7 shows computational times for NSGA-II is 2–5 times more than decomposition methods computational times. Since, NSGA-II searches more regions of solutions space, and finds greater number of non-dominated solutions, this higher computational time is reasonable. The final Pareto front solutions for the problem number 13 are shown in Fig 8.

Table 6 Average computational times (in seconds)
Full size table
Table 7 Computational results for large size problems
Full size table
Fig. 8
figure 8

Pareto-front solutions for large scale problem for problem 13

Full size image

Conclusion and future research

We considered the waste collection problem with particular assumptions in the framework of location routing problem. Collection and treatment of wastes were performed in two Stages. Stage one included Collecting of wastes from customers’ location and second stage included transferring of waste from customers’ location to compatible treatment facility for each type of the waste. Also, the appropriate location for establishing depots and treatment facilities should be chosen from potential locations. Combination of open routes (for external vehicles) and close routes (for internal vehicles) was addressed simultaneously. Moreover, vehicles were considered to be multi compartments; that is, each vehicle has a specific capacity for each type of waste. A new mathematical model was presented in order to facilitate understanding of the problem. This article proposed a meta-heuristic algorithms for solving a bi-objective problem (hybrid NSGA-II). The NSGA-II was combined with clustering method to reach better solutions. To validate the proposed algorithms various test problems were designed and the algorithms were compared to decomposition methods by means of comparisons metrics such as number of Pareto solutions(NPS), two pacing metrics (SM1, SM2) and diversification metric(DM). Decomposition methods included weighted sum, goal programming and goal attainment methods which are less considered in previous articles. The experimental results showed that the proposed hybrid NSGA-II outperformed all decomposition methods in small and large sized test problems, but the computational times for decomposition methods were smaller than hybrid NSGA-II and this was rational according to this fact that NSGA-II could search more regions of solutions area.

For future research, we suggest to researcher and others who are interested in this field of logistics to combine available constraints with other constraints such as hard or soft time windows constraint. Time is critical factor in waste collection problem and attention to this constraint is more realistic and could cover real world problems. In addition, the vehicles can be seen heterogeneous with different capacity and different time and distance limitations. Almost in real world applications the fleet of vehicles is heterogeneous with different limitations. Other multi objective evolutionary algorithms can be used to solve the problem and the results can be compared with each other.