TOPSIS approach to linear fractional bi-level MODM problem based on fuzzy goal programming

Abstract

The objective of this paper is to present a technique for order preference by similarity to ideal solution (TOPSIS) algorithm to linear fractional bi-level multi-objective decision-making problem. TOPSIS is used to yield most appropriate alternative from a finite set of alternatives based upon simultaneous shortest distance from positive ideal solution (PIS) and furthest distance from negative ideal solution (NIS). In the proposed approach, first, the PIS and NIS for both levels are determined and the membership functions of distance functions from PIS and NIS of both levels are formulated. Linearization technique is used in order to transform the non-linear membership functions into equivalent linear membership functions and then normalize them. A possible relaxation on decision for both levels is considered for avoiding decision deadlock. Then fuzzy goal programming models are developed to achieve compromise solution of the problem by minimizing the negative deviational variables. Distance function is used to identify the optimal compromise solution. The paper presents a hybrid model of TOPSIS and fuzzy goal programming. An illustrative numerical example is solved to clarify the proposed approach. Finally, to demonstrate the efficiency of the proposed approach, the obtained solution is compared with the solution derived from existing methods in the literature.

Introduction

Bi-level programming is recognized as a powerful mathematical apparatus for modeling decentralized decisions with two decision makers (DMs) in a large hierarchical organization. Bi-level programming problems (BLPPs) have the following common features: the first-level decision maker (FLDM) or the leader and the second-level decision maker (SLDM) or the follower independently controls a set of decision variables; each DM tries to maximize his/her own interest, but the decision of each DM is affected by the action and reaction of the other DM; each DM should have an intention to cooperate each other in the decision-making situation. Bi-level programming has been applied to model real-world problems regarding flow shop scheduling (Karlof and Wang 1996), bio-fuel production (Bard et al. 2000), natural gas cash-out (Dempe et al. 2005), logistics (Huijun et al. 2008), pollution emission price (Wang et al. 2011), etc. Lai (1996) introduced the concept of tolerance membership function of fuzzy set theory to multi-level programming problems (MLPPs) for satisfactory decisions. Shih et al. (1996) extended Lai’s satisfactory solution concept and proposed a supervised search approach to MLPPs based on max–min aggregation operator. Shih and Lee (2000) further extended Lai’s satisfactory solution concept and presented a solution methodology for MLPPs using compensatory fuzzy operator. Sinha (2003a, b) developed an alternative fuzzy mathematical programming to MLPPs where the decision of lower-level DM is most important and the decision power of lower-level DM dominates the FLDM. Sakawa et al. (1998) developed interactive fuzzy programming algorithm to solve MLPPs by deleting the fuzzy goals for the decision variables to overcome the problem in the methods of Lai (1996). Pramanik and Roy (2007) proposed a methodology based on fuzzy goal programming (FGP) approach to MLPPs by considering the relaxation of decision of the FLDM and solved the problem by minimizing the negative deviational variables. In this article, we have considered linear fractional bi-level multi-objective decision-making (BL-MODM) problem where each level DM possesses multiple linear fractional objective functions with common linear constraints. However, in contrast to linear BLPPs, only some methodological developments for fuzzy linear fractional BLPPs/decentralized BLPPs have appeared in the literature (Sakawa and Nishizaki 2002, 2001; Ahlatcioglu and Tiryaki 2007; Mishra 2007; Toksarı 2010; Pramanik and Dey 2011b; Pramanik et al. 2012). Baky (2009) presented an algorithm to solve decentralized BL-MODM problem by extending the FGP approach incorporated by Mohamed (1997) and the proposed approach is also extended for solving linear fractional decentralized BL-MODM problem. Abo-Sinna and Baky (2010) presented a FGP procedure to linear fractional BL-MODM problem using the method of variable change on the negative and positive deviational variables.

In the field of multi-attribute decision-making, Hwang and Yoon (1981) introduced the concept of technique for order preference by similarity to ideal solution (TOPSIS) for obtaining compromise solution. TOPSIS is based upon the principle that the chosen alternative should have the minimum distance from positive ideal solution (PIS) and maximum distance from negative ideal solution (NIS). In real-life decision-making situation, a DM desires to obtain a decision that not only offers as much return as possible but also reduces as much risk as possible. Generally, TOPSIS converts M number of conflicting and non commensurable objectives (criteria) into two commensurable and most of time conflicting objectives (the minimum distance from PIS and the maximum distance from NIS) (Abo-Sinna and Amer 2005). Lai et al. (1994) presented a methodology based on the extended TOPSIS method for solving multi-objective decision-making (MODM) problem. Chen (2000) extended the concept of TOPSIS in order to formulate a methodology for solving multi-person multi-criteria decision-making (MCDM) problems in fuzzy environment. Abo-Sinna and Amer (2005) and Abo-Sinna et al. (2008) studied the extensions of TOPSIS for solving multi-objective large-scale non-linear programming problems with block angular structure. Recently, Baky and Abo-Sinna (2013) proposed a fuzzy TOPSIS algorithm for solving non-linear BL-MODM problems. In their approach, they extended the TOPSIS to first (upper)-level MODM problem for obtaining the satisfying solution for FLDM. Then the linear membership functions of variables under the control of the FLDM are formulated. Finally, max–min decision model of the BL-MODM problem is solved in order to generate the satisfactory solution of the problem.

In this paper, the TOPSIS approach to solve linear fractional BL-MODM problem based on FGP technique is extended. In the proposed approach, fuzzy TOPSIS models for both level DMs are developed and satisfactory solutions for both levels are obtained. Possible relaxations on decisions for both levels are considered. Thereafter, FGP models are formulated and the linear fractional BL-MODM problem is solved by minimizing the negative deviational variables.

Rest of the paper is organized as follows: In the Sect. “Problem formulation”, we present the formulation of BL-MODM problem. Some basic concepts of the distance measures of ‘closeness’ and its normalization are provided in the subsequent sections. TOPSIS approaches for first-level DM and second-level DM are discussed in the next two sections, respectively. Section “Preference bounds for FLDM and SLDM” briefly discusses the necessity for providing preference upper and lower bounds for both level DMs. In the Sect. “FGP approach for BL-MODM problem”, we have formulated the FGP models for BL-MODM problem. The next section presents the TOPSIS algorithm for BL-MODM problem based on FGP procedure. Section “Selection of optimal compromise solution” provides the selection criteria in order to achieve optimal compromise solution of the problem. In the Sect. “Numerical example”, a numerical example is solved to illustrate the proposed methodology. Finally, the last section concludes the paper with future direction of research.

Materials and methods

Problem formulation

Assume that there are two levels in a hierarchy structure with a FLDM at the first level and a SLDM at the second level. The FLDM controls the decision vector $x_1=(x_{11},x_{12},\dots ,x_{1N_1})\in R^{N_1}$ and the SLDM controls the decision vector $x_2=(x_{21},x_{22},\dots ,x_{2N_2})\in R^{N_2}$, where N = N₁ + N₂. Also we assume that Z₁ (x₁, x₂): $R^{N_1}\times R^{N_2}\to R^{M_i}$, i = 1, 2.

The linear fractional BL-MODM problem of maximization-type objective function at each level can be formulated as:

[First level]

$$\underset{x_1}{\text{Max}}{Z}_1\left(x\right)=\underset{x_1}{\text{Max}}{Z}_1\left(x_1,x_2\right)=\underset{x_1}{\text{Max}}\left(z_{11}\left(x_1,x_2\right),z_{12}\left(x_1,x_2\right),\dots ,z_{1M_1}\left(x_1,x_2\right)\right)$$

(1)

[Second level]

$$\underset{x_2}{\text{Max}}{Z}_2\left(x\right)=\underset{x_2}{\text{Max}}{Z}_2\left(x_1,x_2\right)=\underset{x_2}{\text{Max}}{z}_{21}\left(\left(x_1,x_2\right),{\text{z}}_{22}\left(x_1,x_2\right),\dots ,z_{2M_2}\left(x_1,x_2\right)\right)$$

(2)

Subject to

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

(3)

where $z_{ij}\left(x_1,x_2\right)=\frac{C_{ij}x+{\mathit{\rho }}_{ij}}{D_{ij}x+{\mathit{\delta }}_{ij}},(i=1,2;j=1,2,\dots ,M_i).$

Here, S is the non-empty convex constraint set, M₁ and M₂ are the number of objective functions of FLDM and SLDM, respectively, and M is the number of constraints. Also, A_i is the $M\times N_{\text{i}}$ matrix, (i = 1, 2); C_ij, $D_{\text{ij}}\in R^N$; ${\mathit{\rho }}_{ij},{\mathit{\delta }}_{ij},(i=1,2;j=1,2,\dots ,M_i)$ are scalars. We also assume that $D_{ij}x+{\mathit{\delta }}_{ij}>0,(i=1,2;j=1,2,\dots ,M_i)$ for all $x\in S$.

Some basic concepts regarding distance measures

Some basis concepts related to distance measure are presented in this section, for further details see Abo-Sinna and Amer (2005) and Abo-Sinna et al. (2008). Let Z(x) = (z₁ (x), z₂ (x), …, z_M (x)) be the vector of the objective functions. Suppose that $Z^{+}=z_1^{+},z_2^{+},\dots ,z_M^{+}$ be the ideal solution or PIS of the vector of the objective functions such that $z_j^{+}=\underset{}{{\text{Max}}_{x\in \text{S}}}{z}_j\left(x\right),(j=1,2,\dots ,M)$. Also, let ($Z^{-}=z_1^{-},z_2^{-},\dots ,z_M^{-}$) be the anti-ideal solution or NIS of the vector of the objective functions such that $z_j^{-}=\underset{}{{\text{Min}}_{x\in S}}{z}_j\left(x\right)$, (j = 1, 2, …, M). Now L_Q-metric is employed in order to achieve the measure of “closeness”. L_Q-metric defines the distance between Z (x) and Z⁺ as follows:

$$d_q={\left\{\sum _{j=1}^M{\mathit{\alpha }}_j^q{\left(z_j^{+}-z_j(x)\right)}^q\right\}}^{\frac{1}{q}},q=1,2,\dots ,\infty .$$

(4)

Here, ${\mathit{\alpha }}_j^q$ (j = 1, 2, …, M; q = 1, 2, …, ∞) represents the relative weight of the jth objective function. However, if the objective function z _j (x), (j = 1, 2, …, M) is not expressed in commensurable unit, then the following metric can be utilized:

$$d_q={\left\{\sum _{j=1}^M{\mathit{\alpha }}_j^q{\left(\frac{z_j^{+}-z_j(x)}{z_j^{+}-z_j^{-}}\right)}^q\right\}}^{\frac{1}{q}},q=1,2,\dots ,\infty .$$

(5)

The compromise solution is defined as the solution, which is nearest to the ideal solution by some distance measure (Abo-Sinna and Amer 2005). We are now interested in obtaining the compromise solution of the following MODM problem:

$$\text{Max}Z\left(x\right)=\left(z_1\left(x\right),z_2\left(x\right),\dots ,z_M\left(x\right)\right)$$

(6)

Subject to

$$x\in S=\left\{x\in R^N|Ax\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\}.$$

Different multi-objective methods such as global criterion method, goal programming method, fuzzy programming method, and interactive method utilize the distance family (4) and (5) in order to yield the compromise solution of a MODM problem when the ideal solution ($Z^{+}=z_1^{+},z_2^{+},\dots ,z_{\text{M}}^{+}$) is the reference point. According to Lai et al. (1994), the problem (6) reduces to the following auxiliary problem:

$$\text{Min}{d}_q={\left\{\sum _{j=1}^M{\mathit{\alpha }}_j^q{\left(\frac{z_j^{+}-z_j(x)}{z_j^{+}-z_j^{-}}\right)}^q\right\}}^{\frac{1}{q}},(q=1,2,\dots ,\infty )$$

(7)

Subject to

$$x\in S=\left\{x\in R^N|Ax\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\}$$

Here, the parameter q represents the ‘balancing factor’ between the group benefit and maximal individual regret. As the value of q increases, the group benefit, i.e., d _q decreases. When q = 1, then an equal importance or weight is given to each deviation and when q = 2, then each deviation is weighted proportionately with the maximum deviation with the maximum importance or weight (Lai et al. 1994).

TOPSIS method for first-level MODM problem

Consider the linear fractional BL-MODM problem of FLDM as follows:

$$\underset{x_1}{\text{Max}}{Z}_1\left(x\right)=\underset{x_1}{\text{Max}}{Z}_1\left(x_1,x_2\right)=\underset{x_1}{\text{Max}}(z_{11}\left(x_1,x_2\right),z_{12}\left(x_1,x_2\right),\dots ,z_{1M_1}\left(x_1,x_2\right))$$

(8)

Subject to

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\}$$

TOPSIS model for FLDM can be presented as follows:

$$\text{Min}{d}_q^{\text{PIS(}F)}\left(x\right)$$

(9)

$$\text{Max}{d}_q^{\text{NIS(}F)}\left(x\right)$$

Subject to

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

where $d_q^{\text{PIS(}F)}\left(x\right)={\left\{{\sum }_{j=1}^{M_1}{\mathit{\alpha }}_j^q{\left(\frac{z_{1j}^{+}-z_{1j}(x)}{z_{1j}^{+}-z_{1j}^{-}}\right)}^q\right\}}^{\frac{1}{q}}$ and $d_q^{\text{NIS(}F)}\left(x\right)={\left\{{\sum }_{j=1}^{M_1}{\mathit{\alpha }}_j^q{\left(\frac{z_{1j}(x)-z_{1j}^{-}}{z_{1j}^{+}-{\text{z}}_{1j}^{-}}\right)}^q\right\}}^{\frac{1}{q}}$.

Here, $z_{1j}^{+}=\underset{x\in S}{\mathrm{Max}}{z}_{1j}\left(x\right)$ and $z_{1j}^{-}=\underset{}{{\text{Min}}_{x\in S}}{z}_{1j}\left(x\right)$, (j = 1, 2, …, M₁) are the PIS and NIS for FLDM, respectively.

Let ${\left(d_q^{\text{PIS(}F)}(x)\right)}^{+}=\underset{x\in S}{\mathrm{Min}}{d}_q^{\text{PIS(}F)}\left(x\right)$ and

$${\left(d_q^{\text{PIS(}F)}(x)\right)}^{-}=\underset{x\in S}{\mathrm{Max}}{d}_q^{\text{PIS(}F)}\left(x\right);$$

$${\left(d_q^{\text{NIS(}F)}(x)\right)}^{+}=\underset{x\in S}{\text{Max}}{d}_q^{\text{NIS(}F)}\left(x\right)\text{and}$$

$${\left(d_q^{\text{NIS(}F)}(x)\right)}^{-}=\underset{x\in S}{\text{Min}}{d}_q^{\text{NIS(}F)}\left(x\right)$$

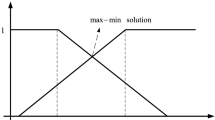
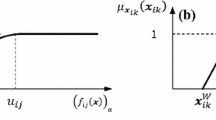
The membership functions for $d_q^{\text{PIS(}F)}$(x) and $d_q^{\text{NIS(}F)}$(x) (see Fig. 1) can be formulated as:

Fig. 1

The membership functions of ${\mathit{\mu }}_{d_q^{\text{PIS}}}(x),{\mathit{\mu }}_{d_q^{\text{NIS}}}(x)$ (Lai et al. 1994)

$${\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x)=\left\{\begin{array}{c}0,if{\left(d_q^{\text{PIS(}F)}(x)\right)}^{-}\le d_q^{\text{PIS(}F)}(x)\\ \frac{{\left(d_q^{\text{PIS(}F)}(x)\right)}^{-}-d_q^{\text{PIS(}F)}(x)}{{\left(d_q^{\text{PIS(}F)}(x)\right)}^{-}-{\left(d_q^{\text{PIS(}F)}(x)\right)}^{+}},if{\left(d_q^{\text{PIS(}F)}(x)\right)}^{+}\le d_q^{\text{PIS(}F)}(x)\\ \le {\left(d_q^{\text{PIS(}F)}(x)\right)}^{-},\\ 1,if{d}_q^{\text{PIS(}F)}(x)\le {\left(d_q^{\text{PIS(}F)}(x)\right)}^{+}\\ \end{array}\right.$$

$${\mathit{\mu }}_{d_q^{\text{NIS(}F)}}(x)=\left\{\begin{array}{c}0,if\left(d_q^{\text{NIS(}F)}(x)\right)\le {\left(d_q^{\text{NIS(}F)}(x)\right)}^{-}\\ \frac{d_q^{\text{NIS(}F)}(x)-{\left(d_q^{\text{NIS(}F)}(x)\right)}^{-}}{{\left(d_q^{\text{NIS(}F)}(x)\right)}^{+}-{\left(d_q^{\text{NIS(}F)}(x)\right)}^{-}},if{\left(d_q^{\text{NIS(}F)}(x)\right)}^{-}\le d_q^{\text{NIS(}F)}(x)\\ \le {\left(d_q^{\text{NIS(}F)}(x)\right)}^{+}\\ 1,if{d}_q^{\text{NIS(}F)}(x)\ge {\left(d_q^{\text{NIS(}F)}(x)\right)}^{+}\\ \end{array}\right.$$

Now we transform the non-linear membership functions ${\mathit{\mu }}_{d_q^{\text{PIS}(F)}}(x)$ and ${\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x)$ into equivalent linear membership functions ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)$, respectively, through first-order Taylor polynomial series as follows:

$${\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x^{\text{PIS}(F)\ast })+\sum _{j=1}^{N_1}(x_{1j}-x_{1j}^{\text{PIS(}F)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x)}{\mathit{\partial }{x}_{1j}}\right)}_{\text{at}x=x^{\text{PIS}(F)\ast }}+\sum _{j=1}^{N_2}(x_{2j}-x_{2j}^{\text{PIS(}F)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x)}{\mathit{\partial }{x}_{2j}}\right)}_{\text{at}x=x^{\text{PIS}(F)\ast }}={\widehat{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x),$$

(10)

where $x^{\text{PIS}(F)\ast }=(x_1^{\text{PIS(}F)\ast },x_2^{\text{PIS(}F)\ast })$ is such that ${\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x^{\text{PIS}(F)\ast })=\underset{}{{\text{Max}}_{x\in \text{S}}}{\mathit{\mu }}_{d_q^{\text{PIS(}F)}}(x)$

$${\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x^{\text{NIS}(F)\ast })+\sum _{j=1}^{N_1}(x_{1j}-x_{1j}^{\text{NIS}(F)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x)}{\mathit{\partial }{x}_{1j}}\right)}_{atx=x^{\text{NIS}(F)\ast }}+\sum _{j=1}^{N_2}(x_{2j}-x_{2j}^{\text{NIS}(F)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x)}{\mathit{\partial }{x}_{2j}}\right)}_{atx=x^{\text{NIS}(F)\ast }}={\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x),$$

(11)

where $x^{\text{NIS}(F)\ast }=(x_1^{\text{NIS(}F)\ast },x_2^{\text{NIS(}F)\ast })$ is such that ${\mathit{\mu }}_{d_q^{\text{NIS(}F)}}(x^{\text{NIS}(F)\ast })=\underset{}{{\text{Max}}_{x\in \text{S}}}{\mathit{\mu }}_{d_q^{\text{NIS(}F)}}(x)$

We now normalize ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS(}F)}}(x)$ according to Stanojević (2013) as follows:

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x)-a^{\text{PIS(}F)}}{b^{\text{PIS(}F)}-a^{\text{PIS(}F)}},$$

${\overline{\mathit{\mu }}}_{d_q^{\text{NIS(}F)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_q^{\text{NIS(}F)}}(x)-a^{\text{NIS(}F)}}{b^{\text{NIS(}F)}-a^{\text{NIS(}F)}},$ where $a^{\text{PIS(}F)}$ and $b^{\text{PIS(}F)}$ are the minimal and maximal values of ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x)$; $a^{\text{NIS(}F)}$ and $b^{\text{NIS(}F)}$ are the minimal and maximal values of ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS(}F)}}(x)$, respectively, subject to the system constraints.

Then to obtain the satisfactory solution of FLDM, we solve the following max–min decision model, according to Bellman and Zadeh (1970) and Zimmermann (1978) as follows:

$${\mathit{\mu }}_{d_q^F}(x)=\underset{}{{\text{Max}}_{x\in \text{S}}}\{\text{Min}({\overline{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x),{\overline{\mathit{\mu }}}_{d_q^{\text{NIS(}F)}}(x))\}.$$

If $\mathit{\beta }=\text{Min}({\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x),{\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)$, then the above model is equivalent to the Tchebycheff model (Lai et al. 1994), which is also equivalent to the following model:

$$\text{Max}\mathit{\beta }$$

(12)

Subject to

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS(}F)}}(x)\ge \mathit{\beta },{\overline{\mathit{\mu }}}_{d_q^{\text{NIS(}F)}}(x)\ge \mathit{\beta },0\le \mathit{\beta }\le 1,$$

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

where $\mathit{\beta }$ represents the satisfactory level for both criteria of the minimal distance from the PIS and maximal distance from the NIS. Let $x^{F^{\ast }}=(x_1^{F^{\ast }},x_2^{F^{\ast }})$ be the satisfactory solution of the FLDM.

TOPSIS method for second-level MODM problem

Consider the linear fractional BL-MODM problem of SLDM as follows:

$$\underset{x_2}{\text{Max}}{Z}_2\left(x\right)=\underset{x_2}{\text{Max}}{Z}_2\left(x_1,x_2\right)=\underset{x_2}{\text{Max}}(z_{21}\left(x_1,x_2\right),z_{22}\left(x_1,x_2\right),\dots ,z_{2M_2}\left(x_1,x_2\right))$$

(13)

Subject to

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\}.$$

TOPSIS model for SLDM can be represented as:

$$\text{Min}{d}_q^{\text{PIS(}S)}\left(x\right)$$

(14)

$$\text{Max}{d}_q^{\text{NIS(}S)}\left(x\right)$$

Subject to

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

where $d_q^{\text{PIS(}S)}\left(x\right)={\left\{{\sum }_{j=1}^{M_2}{\mathit{\alpha }}_j^q{\left(\frac{z_{2j}^{+}-z_{2j}(x)}{z_{2j}^{+}-z_{2j}^{-}}\right)}^q\right\}}^{\frac{1}{q}}$ and $d_q^{\text{NIS(}S)}\left(x\right)={\left\{{\sum }_{j=1}^{M_2}{\mathit{\alpha }}_j^q{\left(\frac{z_{2j}(x)-z_{2j}^{-}}{z_{2j}^{+}-z_{2j}^{-}}\right)}^q\right\}}^{\frac{1}{q}}$.

Here, $z_{2\text{j}}^{+}=\underset{}{{\text{Max}}_{x\in S}}{z}_{2j}\left(x\right)$and $z_{2j}^{-}=\underset{}{{\text{Min}}_{x\in S}}{z}_{2j}\left(x\right)$, (j = 1, 2, …, M₂) are the positive ideal solutions and negative ideal solutions for SLDM, respectively.

Let ${\left(d_q^{\text{PIS(}S)}(x)\right)}^{+}=\underset{x\in S}{\mathrm{Min}}{d}_q^{\text{PIS(}S)}\left(x\right)$ and

$${\left(d_q^{\text{PIS(}S)}(x)\right)}^{-}=\underset{x\in S}{\mathrm{Max}}{d}_q^{\text{PIS(}S)}\left(x\right);$$

$${\left(d_q^{\text{NIS(}S)}(x)\right)}^{+}=\underset{x\in S}{\mathrm{Max}}{d}_q^{\text{NIS(}S)}\left(x\right)\text{and}$$

$${\left(d_q^{\text{NIS(}S)}(x)\right)}^{-}=\underset{x\in S}{\mathrm{Min}}{d}_q^{\text{NIS(}S)}\left(x\right)$$

The membership functions of $d_q^{\text{PIS(}S)}\left(x\right)$ and $d_q^{\text{NIS(}S)}\left(x\right)$ can be formulated as follows:

$${\mathit{\mu }}_{d_q^{\text{PIS(}S)}}(x)=\left\{\begin{array}{c}0,if{\left(d_q^{\text{PIS(}S)}(x)\right)}^{-}\le d_q^{\text{PIS(}S)}(x)\\ \frac{{\left(d_q^{\text{PIS(}S)}(x)\right)}^{-}-d_q^{\text{PIS(}S)}(x)}{{\left(d_q^{\text{PIS(}S)}(x)\right)}^{-}-{\left(d_q^{\text{PIS(}S)}(x)\right)}^{+}},if{\left(d_q^{\text{PIS(}S)}(x)\right)}^{+}\le d_q^{\text{PIS(}S)}(x)\\ \le {\left(d_q^{\text{PIS(}S)}(x)\right)}^{-},\\ 1,if{d}_q^{\text{PIS(}S)}(x)\le {\left(d_q^{\text{PIS(}S)}(x)\right)}^{+}\\ \end{array}\right.$$

$${\mathit{\mu }}_{d_q^{\text{NIS(}S)}}(x)=\left\{\begin{array}{c}0,if\left(d_q^{\text{NIS(}S)}(x)\right)\le {\left(d_q^{\text{NIS(}S)}(x)\right)}^{-}\\ \frac{d_q^{\text{NIS(}S)}(x)-{\left(d_q^{\text{NIS(}S)}(x)\right)}^{-}}{{\left(d_q^{\text{NIS(}S)}(x)\right)}^{+}-{\left(d_q^{\text{NIS(}S)}(x)\right)}^{-}},if{\left(d_q^{\text{NIS(}S)}(x)\right)}^{-}\le d_q^{\text{NIS(}S)}(x)\\ \le {\left(d_q^{\text{NIS(}S)}(x)\right)}^{+}\\ 1,if{d}_q^{\text{NIS(}S)}(x)\ge {\left(d_q^{\text{NIS(}S)}(x)\right)}^{+}\\ \end{array}\right.$$

We again transform the non-linear membership functions ${\mathit{\mu }}_{d_q^{\text{PIS(}S)}}(x)$ and ${\mathit{\mu }}_{d_q^{\text{NIS(}S)}}(x)$ into equivalent linear membership functions ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS(}S)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS(}S)}}(x)$, respectively, via first-order Taylor polynomial series as follows:

$${\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x^{\text{PIS}(S)\ast })+\sum _{j=1}^{N_1}(x_{1j}-x_{1j}^{\text{PIS}(S)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x)}{\mathit{\partial }{x}_{1j}}\right)}_{atx=x^{\text{PIS}(S)\ast }}+\sum _{j=1}^{N_2}(x_{2j}-x_{2j}^{\text{PIS}(S)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x)}{\mathit{\partial }{x}_{2j}}\right)}_{atx=x^{\text{PIS}(S)\ast }}={\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x),$$

(15)

where $x^{\text{PIS}(S)\ast }=(x_1^{\text{PIS(}S)\ast },x_2^{\text{PIS(}S)\ast })$ is such that ${\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x^{\text{PIS}(S)\ast })=\underset{}{{\text{Max}}_{x\in S}}{\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x)$.

$${\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x^{\text{NIS}(S)\ast })+\sum _{j=1}^{N_1}(x_{1j}-x_{1j}^{\text{NIS}(S)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x)}{\mathit{\partial }{x}_{1j}}\right)}_{atx=x^{\text{NIS}(S)\ast }}+\sum _{j=1}^{N_2}(x_{2j}-x_{2j}^{\text{NIS}(S)\ast }){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x)}{\mathit{\partial }{x}_{2j}}\right)}_{atx=x^{\text{NIS}(S)\ast }}={\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x),$$

(16)

where $x^{\text{NIS}(S)\ast }=(x_1^{\text{NIS(}S)\ast },x_2^{\text{NIS(}S)\ast })$ is such that ${\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x^{\text{NIS}(S)\ast })=\underset{}{{\text{Max}}_{x\in S}}{\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x).$

We normalize (Stanojević 2013) ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)$ as follows:

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)-a^{\text{PIS}(S)}}{b^{\text{PIS}(S)}-a^{\text{PIS}(S)}},$$

${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)-a^{\text{NIS}(S)}}{b^{\text{NIS}(S)}-a^{\text{NIS}(S)}}$, where $a^{\text{PIS(}S)}$and $b^{\text{PIS(}S)}$ are the minimal and maximal values of ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)$, respectively, and $a^{\text{NIS(}S)}$ and $b^{\text{NIS(}S)}$ are the minimal and maximal values of ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)$, respectively, over the system constraints.

Now in order to achieve the satisfactory solution of SLDM, we solve the following max–min decision model:

$$\text{Max}\mathit{\lambda }$$

(17)

Subject to

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)\ge \mathit{\lambda },{\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)\ge \mathit{\lambda },0\le \mathit{\lambda }\le 1,$$

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

where $\mathit{\lambda }$ represents the satisfactory level for both criteria of the minimal distance from the PIS and maximal distance from the NIS for SLDM. Let $x^{S^{\ast }}=(x_1^{S^{\ast }},x_2^{S^{\ast }})$ be the maximizing solution of the model (17) and also the satisfactory solution of the SLDM.

Preference bounds for FLDM and SLDM

In a BLPP, the objectives or goals of both level DMs are often conflicting in nature. So, cooperation between both level DMs is necessary for a hierarchical organization in order to sustain in the open and increasing competitive markets. For the smooth functioning and the benefit of the organization, FLDM and SLDM should provide some relaxations on their decisions to reach at a satisfactory solution (Pramanik and Dey 2011a; Mishra 2007). Let $t_{1m}^{L\left(F\right)}$ and $t_{1m}^{R(F)}$, (m = 1, 2, …, N₁) be the lower and upper tolerance values on the decision vector considered by FLDM, where $x_1^{F^{\ast }}$ = ($x_{11}^{F^{\ast }}$, $x_{12}^{F^{\ast }}$, …, $x_{1N_1}^{F^{\ast }}$) such that

$$x_{1m}^{F^{\ast }}-t_{1m}^{L(F)}\le x_{1m}\le x_{1m}^{F^{\ast }}+t_{1m}^{R(F)},\left(m=1,2,\dots ,N_1\right).$$

Also let $t_{2n}^{L(S)}$ and $t_{2n}^{R(S)}$, (n = 1, 2,…, N₂) be the lower and upper tolerance values on the decision vector considered by SLDM, where $x_2^{S^{\ast }}$ = ($x_{21}^{S^{\ast }}$, $x_{22}^{S^{\ast }}$, …, $x_{2N_2}^{S^{\ast }}$) such that

$$x_{2n}^{S^{\ast }}-t_{2n}^{L(F)}\le x_{2n}\le x_{2n}^{S^{\ast }}+t_{2n}^{R(S)},\left(n=1,2,\dots ,N_2\right).$$

Here we consider that both level decision makers provide relaxation on their decision. This happens in real decision-making situation. For example, when FLDM needs extra time duty (overtime duty) from SLDM to produce more production to meet the urgent market demands (because of festivals like Durga puja, Id or other reasons), then it depends upon the decision of the SLDM whether he/she relaxes his decision to perform extra duties. If SLDM relaxes his/her decision to perform overtime duty, it gives the organization opportunity to run smoothly and compete with other organizations. So the relaxation of SLDM is justified.

FGP approach for BL-MODM problem

Now the crisp BL-MODM problem defined in the ‘problem formulation’ section is reduced to the following fuzzy BL-MODM problem as follows:

$$\text{Max}\left\{{\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x),{\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x),{\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x),{\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)\right\}$$

(18)

Subject to

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

$$x_{1m}^{F^{\ast }}-t_{1m}^{L(F)}\le x_{1m}\le x_{1m}^{F^{\ast }}+t_{1m}^{R(F)},\left(m=1,2,\dots ,N_1\right)$$

$$x_{2n}^{S^{\ast }}-t_{2n}^{L(F)}\le x_{2n}\le x_{2n}^{S^{\ast }}+t_{2n}^{R(S)},\left(n=1,2,\dots ,N_2\right).$$

In fuzzy decision-making environment, the objective of each level DM is to obtain maximum possible membership value (one) of the corresponding fuzzy goal. Now, for the defined membership goals in (18), the flexible membership goals according to Pramanik and Roy (2007) with aspiration level one can be formulated as:

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x)+d_{\text{PIS}(F)}^{-}\ge 1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)+d_{\text{NIS}(F)}^{-}\ge 1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)+d_{\text{PIS}(S)}^{-}\ge 1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)+d_{\text{NIS}(S)}^{-}\ge 1.$$

where $d_{\text{PIS(}F)}^{-}$, $d_{\text{NIS(}F)}^{-}$, $d_{\text{PIS(}S)}^{-}$ and $d_{\text{NIS(}S)}^{-}$ (≥0) are the negative deviational variables.

However, Pramanik and Dey (2011a) imposed restriction on the negative deviational variable.

Therefore, the new FGP formulation according to Pramanik and Dey (2011a) for BL-MODM problem can be formulated as follows:

Model (I):

$$\text{Minimize}\mathit{\gamma }=w_1{d}_{\text{PIS(}F)}^{-}+w_2{d}_{\text{NIS(}F)}^{-}+w_3{d}_{\text{PIS(}S)}^{-}+w_4{d}_{\text{NIS(}S)}^{-}$$

(19)

Subject to

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x)+d_{\text{PIS}(F)}^{-}=1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)+d_{\text{NIS}(F)}^{-}=1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)+d_{\text{PIS}(S)}^{-}=1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)+d_{\text{NIS}(S)}^{-}=1,$$

$$0\le d_{\text{PIS(}F)}^{-}\le 1,0\le d_{\text{NIS(}F)}^{-}\le 1,$$

$$0\le d_{\text{PIS(}S)}^{-}\le 1,0\le d_{\text{NIS(}S)}^{-}\le 1,$$

$$x\in S=\left\{x=\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

$$x_{1m}^{F^{\ast }}-t_{1m}^{L(F)}\le x_{1m}\le x_{1m}^{F^{\ast }}+t_{1m}^{R(F)},\left(m=1,2,\dots ,N_1\right)$$

$$x_{2n}^{S^{\ast }}-t_{2n}^{L(F)}\le x_{2n}\le x_{2n}^{S^{\ast }}+t_{2n}^{R(S)},\left(n=1,2,\dots ,N_2\right).$$

Here, the DMs can take the normalized weight, i.e., ${\sum }_{i=1}^4{w}_i=1$ with w _i  = 1/4 or any preference weight in the decision-making environment.

Model (II):

$$\text{Minimize}\mathit{\sigma }$$

(20)

Subject to

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x)+d_{\text{PIS}(F)}^{-}=1$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)+d_{\text{NIS}(F)}^{-}=1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)+d_{\text{PIS}(S)}^{-}=1,$$

$${\overline{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)+d_{\text{NIS}(S)}^{-}=1,$$

$$0\le d_{\text{PIS(}F)}^{-}\le 1,0\le d_{\text{NIS(}F)}^{-}\le 1,$$

$$0\le d_{\text{PIS(}S)}^{-}\le 1,0\le d_{\text{NIS(}S)}^{-}\le 1,$$

$$\mathit{\sigma }\ge d_{\text{PIS(}F)}^{-},\mathit{\sigma }\ge d_{\text{NIS(}F)}^{-},$$

$$\mathit{\sigma }\ge d_{\text{PIS(}S)}^{-},\mathit{\sigma }\ge d_{\text{NIS(}S)}^{-},$$

$$x\in S=x=\left\{\left(x_1,x_2\right)\in R^N|A_1{x}_1+A_2{x}_2\left(\begin{array}{c}\ge \\ =\\ \le \\ \end{array}\right)b,x\ge 0,b\in R^M\right\},$$

$$x_{1m}^{F^{\ast }}-t_{1m}^{L(F)}\le x_{1m}\le x_{1m}^{F^{\ast }}+t_{1m}^{R(F)},\left(m=1,2,\dots ,N_1\right)$$

$$x_{2n}^{S^{\ast }}-t_{2n}^{L(F)}\le x_{2n}\le x_{2n}^{S^{\ast }}+t_{2n}^{R(S)},\left(n=1,2,\dots ,N_2\right).$$

Selection of optimal compromise solution

To obtain the optimal compromise solution of problem, the family of distance functions (Zeleny 1982) is defined as follows:

$$L_r(\mathit{\tau },k)={\left(\sum _{k=1}^K{\mathit{\tau }}_k^r{(1-{\mathit{\omega }}_k)}^r\right)}^{1/\phantom{1r}r}$$

(21)

Here, ${\mathit{\omega }}_k$ (k = 1, 2, …, K) denotes the degree of closeness of the preferred compromise solution to the optimal compromise solution vector with respect to kth objective function. Also, $\mathit{\tau }$ = (${\mathit{\tau }}_1$,${\mathit{\tau }}_2$,…, ${\mathit{\tau }}_K$) represents the vector of attribute level ${\mathit{\tau }}_k$ such that ${\sum }_{k=1}^K{\mathit{\tau }}_k$ = 1. If all the attribute levels ${\mathit{\tau }}_k$ are same, then ${\mathit{\tau }}_k$ = 1/K for k = 1, 2, …, K. Here, $r(1\underset{=}{\le }r\underset{=}{\le }\infty )$ denotes the distance parameter.

Now for r = 2, the family of distance functions become

$$L_2(\mathit{\tau },k)={\left(\sum _{k=1}^K{\mathit{\tau }}_k^2{(1-{\mathit{\omega }}_k)}^2\right)}^{1/\phantom{12}2}$$

(22)

For minimization type problem, ${\mathit{\omega }}_k$ = (the individual best solution/the preferred compromise solution) and maximization type of problem ${\mathit{\omega }}_k$ = (the preferred compromise solution/the individual best solution). The solution for which $L_2(\mathit{\tau },k)={\left({\sum }_{k=1}^K{\mathit{\tau }}_k^2{(1-{\mathit{\omega }}_k)}^2\right)}^{1/\phantom{12}2}$ will be minimal would be the optimal compromise solution for the problem.

The TOPSIS algorithm for solving linear fractional BL-MODM problem

We now present the TOPSIS algorithm for solving linear fractional BL-MODM problem based on FGP technique by the following steps:

Step 1: Determine the individual maximum and minimum values of all the objective functions for both level DMs subject to the system constraints.

Step 2: Identify the positive ideal solution and negative ideal solution for FLDM and construct $d_q^{\text{PIS}(F)}\left(x\right)$ and $d_q^{\text{NIS}(F)}\left(x\right)$ for FLDM.

Step 3: Ask the DMs to select q (q = 1, 2, …, ∞).

Step 4: Calculate the maximum and minimum values of $d_q^{\text{PIS}(F)}\left(x\right)$ and $d_q^{\text{NIS}(F)}\left(x\right)$ subject to the system constraints.

Step 5: Formulate the membership functions ${\mathit{\mu }}_{d_q^{\text{PIS}(F)}}(x)$ and ${\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x)$.

Step 6: Linearize the non-linear membership functions ${\mathit{\mu }}_{d_q^{\text{PIS}(F)}}(x)$ and ${\mathit{\mu }}_{d_q^{\text{NIS}(F)}}(x)$ into equivalent linear membership functions ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)$, respectively, using first-order Taylor polynomial series.

Step 7: Normalize ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(F)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(F)}}(x)$.

Step 8: Formulate the model (12) and solve the model to find the satisfactory solution $x^{F^{\ast }}=(x_1^{F^{\ast }},x_2^{F^{\ast }})$ of FLDM.

Step 9: FLDM provides the negative and positive tolerance values $t_{1m}^{L(F)}$ and $t_{1m}^{R(F)}$ (m = 1, 2, …, N₁), respectively, on the decision vector $x_1^{F^{\ast }}=(x_{11}^{F^{\ast }},x_{12}^{F^{\ast }},\dots ,x_{1N_1}^{F^{\ast }})$.

Step 10: Find the positive ideal solution and negative ideal solution for SLDM and construct $d_q^{\text{PIS}(S)}\left(x\right)$ and $d_q^{\text{NIS}(S)}\left(x\right)$ for SLDM.

Step 11: Calculate the maximum and minimum values of $d_q^{\text{PIS}(S)}\left(x\right)$ and $d_q^{\text{NIS}(S)}\left(x\right)$ subject to the system constraints.

Step 12: Construct the membership functions ${\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x)$ and ${\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x)$.

Step 13: Linearize the non-linear membership functions ${\mathit{\mu }}_{d_q^{\text{PIS}(S)}}(x)$ and ${\mathit{\mu }}_{d_q^{\text{NIS}(S)}}(x)$ into equivalent linear membership functions ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)$, respectively, by utilizing first-order Taylor polynomial series.

Step 14: Normalize ${\widehat{\mathit{\mu }}}_{d_q^{\text{PIS}(S)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS}(S)}}(x)$.

Step 15: Formulate the model (17) and solve the model to obtain the satisfactory solution $x^{S^{\ast }}=(x_1^{S^{\ast }},x_2^{S^{\ast }})$ of SLDM.

Step 16: SLDM presents the negative and positive tolerance values $t_{2n}^{L(S)}$ and $t_{2n}^{R(S)},\left(n=1,2,\dots ,N_2\right)$, respectively, on the decision vector $x_2^{S^{\ast }}=(x_{21}^{S^{\ast }},x_{22}^{S^{\ast }},\dots ,x_{2N_2}^{S^{\ast }})$.

Step 17: Formulate the FGP models (19) and (20) for linear fractional BL-MODM problem.

Step 18: Solve the FGP models (19) and (20) to obtain the compromise solution of the BL-MODM problem.

Step 19: Distance function L₂ ($\mathit{\tau }$, k) is utilized in order to recognize the optimal compromise solution of the problem.

Step 20: If the solution is acceptable to both level DMs then stop. Otherwise, modify the lower and upper preference values of both level DMs and go to Step 17.

Results and discussion

Numerical example

Consider the following numerical example studied by Dey et al. (2013) with some changes in the first objective function of SLDM in order to clarify the proposed procedure.

[First level]

$$\underset{x_1}{\text{Max}}\left(z_{11}\left(x\right)=\frac{5x_1+2x_2+3}{2x_1-x_2+3},z_{12}\left(x\right)=\frac{2x_1+5x_2+3}{x_1+4x_2+4}\right)$$

[Second level]

$$\underset{x_2}{\text{Max}}\left(z_{21}\left(x\right)=\frac{3x_1+2x_2}{x_1+5x_2+1},z_{22}\left(x\right)=\frac{-x_1+4x_2+3}{x_1+2x_2}\right)$$

Subject to

$$2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,x_1\ge 0,x_2\ge 0.$$

First-level MODM problem:

$$\underset{x_1}{\text{Max}}\left(z_{11}\left(x\right)=\frac{5x_1+2x_2+3}{2x_1-x_2+3},z_{12}\left(x\right)=\frac{2x_1+5x_2+3}{x_1+4x_2+4}\right)$$

Subject to

$$2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,x_1\ge 0,x_2\ge 0.$$

The individual best (maximum) solution (PIS) of the objective functions subject to the constraints is $z_{11}^{+}$ = 3.029 at (1.714, 1.571) and $z_{12}^{+}$ = 1.231 at (2.5, 0) and the individual worst (minimum) solution (NIS) of the objective functions subject to the constraints is $z_{11}^{-}$ = 1.6 at (1, 0) and $z_{12}^{-}$ = 1 at (0.251, 0.749).

Let us assume that ${\mathit{\alpha }}_1$ = ${\mathit{\alpha }}_2$ = 0.5, and q = 2.

$$d_2^{\text{PIS}(F)}(x)={\left\{\begin{array}{c}{(0.5)}^2{\left[\frac{3.029-\frac{5x_1+2x_2+3}{2x_1-x_2+3}}{3.029-1.6}\right]}^2+\\ {(0.5)}^2{\left[\frac{1.231-\frac{2x_1+5x_2+3}{x_1+4x_2+4}}{1.231-1}\right]}^2\\ \end{array}\right\}}^{1/\phantom{12}2},$$

$$d_2^{\text{NIS}(F)}(x)={\left\{\begin{array}{c}{(0.5)}^2{\left[\frac{\frac{5x_1+2x_2+3}{2x_1-x_2+3}-1.6}{3.029-1.6}\right]}^2+\\ {(0.5)}^2{\left[\frac{\frac{2x_1+5x_2+3}{x_1+4x_2+4}-1}{1.231-1}\right]}^2\\ \end{array}\right\}}^{1/\phantom{12}2}.$$

Also we determine: ${\left(d_2^{\text{PIS}(F)}(x)\right)}^{+}=\underset{}{{\text{Min}}_{x\in S}}{d}_2^{\text{PIS}(F)}\left(x\right)=0.087$ at (1.723, 1.554); ${\left(d_2^{\text{PIS}(F)}(x)\right)}^{-}=\underset{}{{\text{Max}}_{x\in S}}{d}_2^{\text{PIS}(F)}\left(x\right)=0.707$ at (1, 0);${\left(d_2^{\text{NIS}(F)}(x)\right)}^{+}=\underset{}{{\text{Max}}_{x\in S}}{d}_2^{\text{NIS}(F)}\left(x\right)=0.648$ at (1.714, 1.571); ${\left(d_2^{\text{NIS}(F)}(x)\right)}^{-}=\underset{}{{\text{Min}}_{x\in S}}{d}_2^{\text{NIS}(F)}\left(x\right)=0$ at (1, 0).

The membership functions of $d_2^{\text{PIS(}F)}$(x) and $d_2^{\text{NIS(}F)}$(x) can be formulated as follows:

$${\mathit{\mu }}_{d_2^{\text{PIS}(F)}}(x)=\left\{\begin{array}{c}0,if0.707\le d_2^{\text{PIS}(F)}(x)\\ \frac{0.707-d_2^{\text{PIS}(F)}(x)}{0.707-0.087},if0.087\le d_2^{\text{PIS}(F)}(x)\le 0.707\\ 1,if{d}_2^{\text{PIS}(F)}(x)\le 0.087\\ \end{array}\right.,$$

$${\mathit{\mu }}_{d_2^{\text{NIS}(F)}}(x)=\left\{\begin{array}{c}0,if\left(d_2^{\text{NIS}(F)}(x)\right)\le 0\\ \frac{d_2^{\text{NIS}(F)}(x)-0}{0.648-0},if0\le d_2^{\text{NIS}(F)}(x)\le 0.648\\ 1,if{d}_2^{NIS(F)}(x)\ge 0.648\\ \end{array}\right.$$

Transform the non-linear membership functions ${\mathit{\mu }}_{d_2^{\text{PIS}(F)}}(x)$ and ${\mathit{\mu }}_{d_2^{\text{NIS}(F)}}(x)$ into equivalent linear membership functions ${\widehat{\mathit{\mu }}}_{d_2^{\text{PIS}(F)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_2^{\text{NIS}(F)}}(x)$, respectively, by applying first-order Taylor polynomial series as follows:

${\mathit{\mu }}_{d_2^{\text{PIS}(F)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_2^{\text{PIS}(F)}}$ (1.723, 1.554) + (x₁ − 1.723) ${\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{PIS}(F)}}(x)}{\mathit{\partial }{x}_1}\right)}_{atx=(1.723,1.554)}$ + (x₂ − 1.554) ${\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{PIS}(F)}}(x)}{\mathit{\partial }{x}_2}\right)}_{atx=(1.723,1.554)}={\widehat{\mathit{\mu }}}_{d_2^{\text{PIS}(F)}}(x)$ = 1 + (x₁ − 1.723) × 0.226 + (x₂ − 1.554) × 0.113, where $\underset{}{{\text{Max}}_{x\in S}}{\mathit{\mu }}_{d_2^{\text{PIS}(F)}}(x)$ = 1 at $x^{\text{PIS}(F)\ast }$ = (1.723, 1.554),

${\mathit{\mu }}_{d_2^{\text{NIS}(F)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_2^{\text{NIS}(F)}}$ (1.714, 1.571) + (x₁ − 1.714) ${\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{NIS}(F)}}(x)}{\mathit{\partial }{x}_1}\right)}_{atx=(1.714,1.571)}$ + (x₂ − 1.571) ${\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{NIS}(F)}}(x)}{\mathit{\partial }{x}_2}\right)}_{atx=(1.714,1.571)}={\widehat{\mathit{\mu }}}_{d_2^{\text{NIS}(F)}}(x)$ = 1 + (x₁ − 1.714) × 0.053 + (x₂ − 1.571) × 0.474, where $\underset{x\in S}{\text{Max}}{\mathit{\mu }}_{d_2^{\text{NIS(}F)}}(x)$ = 1 at $x^{\text{NIS}(F)\ast }$ = (1.714, 1.571).

Normalize ${\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}F)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}F)}}(x)$:

${\overline{\mathit{\mu }}}_{d_2^{\text{PIS(}F)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}F)}}(x)-a^{\text{PIS(}F)}}{b^{\text{PIS(}F)}-a^{\text{PIS(}F)}}$, where $b^{\text{PIS}(F)}=\underset{x\in S}{\mathrm{Max}}{\widehat{\mathit{\mu }}}_{d_2^{\text{PIS}(F)}}(x)=1$ and $a^{\text{PIS}(F)}=\underset{x\in S}{\mathrm{Min}}{\widehat{\mathit{\mu }}}_{d_2^{\text{PIS}(F)}}(x)$= 0.548;

$${\overline{\mathit{\mu }}}_{d_2^{\text{NIS}(F)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_2^{\text{NIS}(F)}}(x)-a^{\text{NIS}(F)}}{b^{\text{NIS}(F)}-a^{\text{NIS}(F)}},\text{where}$$

$$b^{\text{NIS(}F)}=\underset{x\in S}{\mathrm{Max}}{\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}F)}}(x)=1\text{and}$$

$$a^{\text{NIS(}F)}=\underset{x\in S}{\mathrm{Min}}{\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}F)}}(x)=0.218.$$

Solve the following model in order to get the satisfactory solution of FLDM:

$$\text{Max}\mathit{\beta }$$

Subject to

$$\begin{array}{c}{\overline{\mathit{\mu }}}_{d_2^{\text{PIS}(F)}}(x)\ge \mathit{\beta },{\overline{\mathit{\mu }}}_{d_2^{\text{NIS}(F)}}(x)\ge \mathit{\beta },0\le \mathit{\beta }\le 1,\\ 2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,x_1\ge 0,x_2\ge 0.\\ \end{array}$$

We get the satisfactory solution of the FLDM as $x^{F^{\ast }}$ = ($x_1^{F^{\ast }}$,$x_2^{F^{\ast }}$) = (1.714, 1.571) with $\mathit{\beta }$ = 1. Suppose that the FLDM decides $x_1^{F^{\ast }}$ = 1.714 with upper tolerance $t_1^{R(F)}$ = 0.286 and lower tolerance $t_1^{L(F)}$ = 0.214 such that 1.714 − 0.214 ≤ x₁ ≤1.714 + 0.286.

Second-level MODM problem:

$$\underset{x_2}{\text{Max}}\left(z_{21}\left(x\right)=\frac{3x_1+2x_2}{x_1+5x_2+1},z_{22}\left(x\right)=\frac{-x_1+4x_2+3}{x_1+2x_2}\right)$$

Subject to

$$2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,x_1\ge 0,x_2\ge 0.$$

The individual best solution of the objective functions of SLDM subject to the constraints is $z_{21}^{+}$ = 2.143 at (2.5, 0) and $z_{22}^{+}$ = 3.5 at (0, 1) and the individual worst solution of the objective functions of SLDM subject to the constraints is $z_{21}^{-}$ = 0.333 at (0, 1) and $z_{22}^{-}$ = 0.2 at (2.5, 0).

$$d_2^{\text{PIS}(S)}(x)={\left\{\begin{array}{c}{(0.5)}^2{\left[\frac{2.143-\frac{3x_1+2x_2}{x_1+5x_2+1}}{2.143-0.333}\right]}^2\\ +{(0.5)}^2{\left[\frac{3.5-\frac{-x_1+4x_2+3}{x_1+2x_2}}{3.5-0.2}\right]}^2\\ \end{array}\right\}}^{1/\phantom{12}2}$$

$$d_2^{\text{NIS}(S)}(x)={\left\{\begin{array}{c}{(0.5)}^2{\left[\frac{\frac{3x_1+2x_2}{x_1+5x_2+1}-0.333}{2.143-0.333}\right]}^2\\ +{(0.5)}^2{\left[\frac{\frac{-x_1+4x_2+3}{x_1+2x_2}-0.2}{3.5-0.2}\right]}^2\\ \end{array}\right\}}^{1/\phantom{12}2}$$

Also we calculate: ${\left(d_2^{\text{PIS(}S)}(x)\right)}^{+}=\underset{}{{\text{Min}}_{x\in S}}{d}_2^{\text{PIS(}S)}\left(x\right)=0.288$ at (1, 0); ${\left(d_2^{\text{PIS(}S)}(x)\right)}^{-}=\underset{}{{\text{Max}}_{x\in S}}{d}_2^{\text{PIS(}S)}\left(x\right)=0.477$ at (1.714, 1.571);${\left(d_2^{\text{NIS(}S)}(x)\right)}^{+}=\underset{}{{\text{Max}}_{x\in S}}{d}_2^{\text{NIS(}S)}\left(x\right)=0.5$ at (0, 1); ${\left(d_2^{\text{NIS(}S)}(x)\right)}^{-}=\underset{}{{\text{Min}}_{x\in S}}{d}_2^{\text{NIS(}S)}\left(x\right)=0.238$ at (1.847, 1.305).

The membership functions of $d_2^{\text{PIS(}S)}$(x) and $d_2^{\text{NIS(}S)}$(x) can be constructed as:

$${\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)=\left\{\begin{array}{ccc}0,& if& 0.477\le d_2^{\text{PIS(}S)}(x)\\ \frac{0.477-d_2^{\text{PIS(}S)}(x)}{0.477-0.288}& if,& 0.288\le d_2^{\text{PIS(}S)}(x)\le 0.477\\ 1,& if& d_2^{\text{PIS(}S)}(x)\le 0.288\end{array}\right.,$$

$${\mathit{\mu }}_{d_2^{\text{NIS(}S)}}(x)=\left\{\begin{array}{ccc}0,& if& \left(d_2^{\text{NIS(}S)}(x)\right)\le 0.238\\ \frac{d_2^{\text{NIS(}S)}(x)-0.238}{0.5-0.238},& if,& 0.238\le d_2^{\text{NIS(}S)}(x)\le 0.5\\ 1,& if& d_2^{\text{NIS(}S)}(x)\ge 0.5\end{array}\right.$$

We also transform the non-linear membership functions ${\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)$ and ${\mathit{\mu }}_{d_2^{\text{NIS(}S)}}(x)$ into equivalent linear membership functions ${\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}S)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_q^{\text{NIS(}S)}}(x)$, respectively, using first-order Taylor polynomial series as:

$${\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_2^{\text{PIS(}S)}}\left(1,0\right)+\left(x_1-1\right)$$

$${\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)}{\mathit{\partial }{x}_1}\right)}_{\text{at}x=(1,0)}+\left(x_2-0\right){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)}{\mathit{\partial }{x}_2}\right)}_{\text{at}x=(1,0)}={\widehat{\mathit{\mu }}}_{d_q^{\text{PIS(}S)}}(x)$$

=1 + (x₁ − 1) × (−1.22) + (x₂ − 0) × (−2.474), where

$$\underset{}{{\text{Max}}_{x\in S}}{\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)=1\text{at}{x}^{\text{PIS}(S)\ast }=\left(1,0\right),$$

$${\mathit{\mu }}_{d_2^{\text{NIS(}S)}}(x)\stackrel{\sim }{=}{\mathit{\mu }}_{d_q^{\text{NIS(}F)}}\left(0,1\right)+\left(x_1-0\right)$$

$${\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{NIS(}S)}}(x)}{\mathit{\partial }{x}_1}\right)}_{\text{at}x=(0,1)}+\left(x_2-0\right){\left(\frac{\mathit{\partial }{\mathit{\mu }}_{d_2^{\text{NIS(}S)}}(x)}{\mathit{\partial }{\text{x}}_2}\right)}_{\text{at}x=(0,1)}$$

$={\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}S)}}(x)=1+\left(x_1-0\right)\times \left(-1.156\right)+\left(x_2-1\right)\times \left(-0.867\right),$ where ${\text{Max}}_{x\in S}$${\mathit{\mu }}_{d_2^{\text{PIS(}S)}}(x)=1$ at $x^{\text{PIS}(S)\ast }=\left(0,1\right).$

Normalize ${\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}S)}}(x)$ and ${\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}S)}}(x)$:

$${\overline{\mathit{\mu }}}_{d_2^{\text{PIS(}S)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}S)}}(x)-a^{\text{PIS(}S)}}{b^{\text{PIS(}S)}-a^{\text{PIS(}S)}},\text{where}$$

$$b^{\text{PIS(}S)}=\underset{x\in S}{\text{Max}}{\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}S)}}(x)=\text{1 and}$$

$$a^{\text{PIS(}S)}=\underset{x\in S}{\text{Min}}{\widehat{\mathit{\mu }}}_{d_2^{\text{PIS(}S)}}(x)=-3.759;$$

$${\overline{\mathit{\mu }}}_{d_2^{\text{NIS(}S)}}(x)=\frac{{\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}S)}}(x)-a^{\text{NIS(}S)}}{b^{\text{NIS(}S)}-a^{\text{NIS(}S)}},\text{where}$$

$$b^{\text{NIS(}S)}=\underset{x\in S}{\text{Max}}{\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}S)}}(x)=\text{1 and}$$

$$a^{\text{NIS(}S)}=\underset{x\in S}{\text{Min}}{\widehat{\mathit{\mu }}}_{d_2^{\text{NIS(}S)}}(x)=-1.477.$$

Solve the following model in order to get the satisfactory solution of SLDM:

$$\text{Max}\mathit{\lambda }$$

Subject to

$${\overline{\mathit{\mu }}}_{d_q^{\text{PIS(}S)}}(x),\ge \mathit{\lambda },{\overline{\mathit{\mu }}}_{d_q^{\text{NIS(}S)}}(x)\ge \mathit{\lambda },0\le \mathit{\lambda }\le 1,$$

$$2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,x_1\ge 0,x_2\ge 0.$$

We obtain the satisfactory solution of the SLDM as $x^{S^{\ast }}=(x_1^{S^{\ast }},x_2^{S^{\ast }})=\left(0.693,0.307\right)$ with $\mathit{\lambda }=0.919$. Also let the SLDM decides $x_2^{S^{\ast }}=0.307$ with upper tolerance $t_2^{R(S)}=0.693$ and lower tolerance $t_2^{L(S)}=0.057$ such that 0.307 − 0.057 ≤ x₂ ≤ 0.307 + 0.693.

Finally, the FGP models for solving linear fractional BL-MODM problem are presented as follows:

Model (I):

$$\text{Minimize}\mathit{\gamma }=1/4(d_{\text{PIS(}F)}^{-}+d_{\text{NIS(}F)}^{-}+d_{\text{PIS(}S)}^{-}+d_{\text{NIS(}S)}^{-})$$

Subject to

$$\left(\left(1+\left(x_1-1.723\right)\times 0.226+\left(x_2-1.554\right)\times 0.113\right)-0.548)\right)/0.452+d_{\text{PIS(}F)}^{-}=1,$$

$$\left(\left(1+\left(x_1-1.714\right)\times 0.053+\left(x_2-1.571\right)\times 0.474\right)-0.218\right)/0.782+d_{\text{NIS(}F)}^{-}=1,$$

$$\left(\left(1+\left(x_1-1\right)\times \left(-1.22\right)+\left(x_2-0\right)\times \left(-2.474\right)\right)+3.759\right)/4.759+d_{\text{PIS}(S)}^{-}=1,$$

$$\left(\left(1+\left(x_1-0\right)\times \left(-1.156\right)+\left(x_2-1\right)\times \left(-0.867\right)\right)+1.477)\right)/2.477+d_{\text{NIS(}S)}^{-}=1,$$

$$0\le d_{\text{PIS(}F)}^{-}\le 1,0\le d_{\text{NIS(}F)}^{-}\le 1,0\le d_{\text{PIS(}S)}^{-}\le 1,0\le d_{\text{NIS(}S)}^{-}\le 1,$$

$$2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,$$

$$1.714-0.214\le x_1\le 1.714+0.286,$$

$$0.307-0.057\le x_2\le 0.307+0.693,$$

$$x_1\ge 0,x_2\ge 0.$$

The solution of the FGP model (I) is presented in Table 1.

Table 1 Comparison of distance for the compromise solution of the problem based on different approaches

Model (II):

$$\text{Minimize}\mathit{\sigma }$$

Subject to

$$\left(\left(1+\left(x_1-1.723\right)\times 0.226+\left(x_2-1.554\right)\times 0.113\right)-0.548\right)/\phantom{\left(\left(1+\left(x_1-1.723\right)\times 0.226+\left(x_2-1.554\right)\times 0.113\right)-0.548\right)0.452+d_{\text{PIS(}F)}^{-}=1,}0.452+d_{\text{PIS(}F)}^{-}=1,$$

$$\left(\left(1+\left(x_1-1.714\right)\times 0.053+\left(x_2-1.571\right)\times 0.474\right)-0.218\right)/\phantom{\left(\left(1+\left(x_1-1.714\right)\times 0.053+\left(x_2-1.571\right)\times 0.474\right)-0.218\right)0.782+d_{\text{NIS(}F)}^{-}=1,}0.782+d_{\text{NIS(}F)}^{-}=1,$$

$$\left(\left(1+\left(x_1-1\right)\times \left(-1.22\right)+\left(x_2-0\right)\times \left(-2.474\right)\right)+3.759\right)/\phantom{\left(\left(1+\left(x_1-1\right)\times \left(-1.22\right)+\left(x_2-0\right)\times \left(-2.474\right)\right)+3.759\right)4.759+d_{\text{PIS(}S)}^{-}=1,}4.759+d_{\text{PIS(}S)}^{-}=1,$$

$$\left(\left((1+\left(x_1-0\right)\times \left(-1.156\right)+\left(x_2-1\right)\times \left(-0.867\right)\right)+1.477\right)/\phantom{\left(\left((1+\left(x_1-0\right)\times \left(-1.156\right)+\left(x_2-1\right)\times \left(-0.867\right)\right)+1.477\right)2.477+d_{\text{NIS(}S)}^{-}=1,}2.477+d_{\text{NIS(}S)}^{-}=1,$$

$$0\le d_{\text{PIS(}F)}^{-}\le 1,0\le d_{\text{NIS(}F)}^{-}\le 1,0\le d_{\text{PIS(}S)}^{-}\le 1,0\le d_{\text{NIS(}S)}^{-}\le 1,$$

$$\mathit{\sigma }\ge d_{\text{PIS(}F)}^{-},\mathit{\sigma }\ge d_{\text{NIS(}F)}^{-},\mathit{\sigma }\ge d_{\text{PIS(}S)}^{-},\mathit{\sigma }\ge d_{\text{NIS(}S)}^{-},$$

$$2x_1+x_2\le 5,-x_1+3x_2\le 3,x_1+x_2\ge 1,$$

$$1.714-0.214\le x_1\le 1.714+0.286,$$

$$0.307-0.057\le x_2\le 0.307+0.693,$$

$$x_1\ge 0,x_2\ge 0.$$

The solution offered by the FGP model (II) is presented in Table 1.

On comparing the distance function (see the Table 1), we observe that our proposed FGP Model (II) offers better compromise optimal solution than the solution obtained by Dey et al. (2013) and Baky and Abo-Sinna (2013). Therefore, the compromise optimal solution of the problem is obtained as x₁ = 1.5, x₂ = 0.645.

Note 1: Solutions of the problem are obtained using software Lingo version 6.

Conclusion

We have presented a new approach for dealing with linear fractional BL-MODM problem. In the paper, we have studied TOPSIS approach for solving linear fractional BL-MODM problem, which is a hybrid model of TOPSIS and fuzzy goal programming. In the proposed approach, first the membership functions of distance functions from PIS and NIS of first and second levels are formulated. Linearization technique is used in order to transform the non-linear membership functions into equivalent linear membership functions using first-order Taylor series approximation and normalization technique (Stanojević 2013) is employed to normalize them. Thereafter, max–min models are formulated in order to obtain the satisfactory decision for each level DM. Both level DMs consider a possible relaxation on their decision for the benefit of the hierarchical organization. The FGP models are then developed in order to achieve highest degree of the membership goals of both level DMs by minimizing negative deviational variables. Distance functions are also utilized to identify optimal compromise solution. Finally, an illustrative numerical example is provided to demonstrate the effectiveness of the proposed TOPSIS approach. We hope that the proposed methodology can be effective in dealing with the non-linear BL-MODM, multi-level MODM problems and other real-world decision-making problems.