Introduction

Tin oxide (SnO2) has been attracting a great deal of research interest owing to its outstanding physical and chemical properties. Investigation has shown that SnO2 has a high exciton binding energy of 130 meV [1], high chemical stability and excellent resistivity variation in a gaseous atmosphere. These intriguing properties make SnO2 a promising candidate for basic research and technological applications alike. Tin oxide is a versatile wide band gap (3.6 eV at 300 K) [2], n-type semiconducting oxide with an extensive potential of applications including solid-state gas sensors [3], dye-based solar cells [4], field emission displays [5], luminescent devices [6]. This oxide is among the few with the band gap energy near to visible light [7, 8]. In the last decade, SnO2 has been studied as promising material with many unique surface properties including luminescence and photocatalytic activity [8, 9]. Adsorption is a conventional but efficient technique to remove heavy metals or organics from aqueous solutions. Adsorption techniques for wastewater treatment have become more popular in recent years owing to their efficiency in the removal of pollutants too stable for biological methods. Recently, enormous efforts have been directed toward the development of size-controlled synthesis of various functional materials in current applications such as microemulsion [4], hydrothermal [10], gel combustion [11], sol-gel and ultrafiltration [12], thermal decomposition [13] and surfactant-assisted solvothermal method [14]. Sol-gel method is one of the most widely used techniques to produce SnO2 powders and factors, such as pH medium, initial concentration, calcinations temperature, and aging time are important to the process [15–17].

Sol-gel method is an outstanding route to the synthesis of hybrid nanoparticles and nanocomposites. Generally speaking it gives inorganic high purity materials at mild synthesis conditions (temperature and pH). An outstanding variation is the so-called Stober method allowing colloidal particles (with well-defined size and shape and with narrow size distribution) be produced through hydrolysis and polycondensation of silicon alkoxides in water/alcohol/ammonia mixtures. The sol-gel method allows, also, easy functionalization of silica nanoparticles with specific organic groups. Many of the hybrid nanoparticles synthesis methods take advantage of all this. The sol-gel method finds, however, applications in many other research fields [18].

In the present study, nanostructured tin oxide (SnO2) was synthesized via a sol-gel method. The as-prepared SnO2 samples were characterized using thermogravimetric analysis coupled with mass spectroscopy (TG-SM), X-ray diffraction (XRD) and scanning electron microscope (SEM). Batch experiments were carried out to study the adsorption kinetics of Congo red azo dye, as probe pollutant, on SnO2. The effect of varying parameters such as contact time, initial dye concentration and adsorbent dose on the adsorption process was investigated. Experimental kinetic data were tested with the pseudo-first-order and pseudo-second-order kinetic equations.

Experimental

Materials

The starting materials were tin dichloride dihydrate (SnCl2·2H2O; 98 wt%) and oxalic acid dihydrate (H2C2O4; 99.5 wt.%) and SnO2 (99.99 wt.%) were all obtained from Aldrich chemical company ltd. Congo red (C.I. 22020, MW = 696.67 g mol−1, C32H24N6O6S2.2Na, λ max = 497 nm and pKa = 4; 99.99 wt%) and other chemicals used in the experiments (NH4OH and H2SO4) were purchased from C.I.S.A Espagne. Distilled water was used for preparation of various solutions. The Congo red dye structure and its characteristics are given in Table 1.

Table 1 The molecular structure and chemical properties of Congo red dye (CR)
Full size table

Preparation of ultrafine n-SnO2

SnO2 was synthesized using co-precipitation method. In a typical synthesis procedure, tin dichloride dehydrate, SnCl2·2H2O, was dissolved in 250 ml of deionized water to reach a Sn(II) concentration of 0.4 M. The obtained white turbid suspension was magnetically stirred for 1 h at room temperature. A stoichiometric amount of oxalic acid, which was used as the chelating agent to complex the cations, then were added dropwise to the aqueous solution of tin dichloride in the molar ratio 1:1 with respect to the cations (Sn). The resulting suspension was kept under stirring for a further 4 h and the precipitate was finally collected by centrifugation, washed with deionized water and ethanol for 3 times in order to remove the excess retained chloride ions. Complete removal of the chloride ions was confirmed with the silver nitrate test applied to the supernatant. The precipitate was washed twice with ethanol to reduce agglomeration by interparticle bridging [19]. The washed precipitate was then dried at 80 °C for 24 h (denoted as SnO2-80) after which it was ground with an agate mortar. The as-synthesized nanostructured SnO2 were heated in temperature range from 450 to 650 °C for 4 h, respectively. The SnO2 samples after annealing (denoted as SnO2-450 and SnO2-650, respectively). The commercial SnO2 sample (denoted as SnO2-com). A schematic illustration of the synthesis method was depicted in Fig. 1.

Fig. 1
figure 1

Schematic illustration of the synthesis of nanostructured SnO2 by a chemical precipitation process

Full size image

Characterization

The crystalline structure of the catalysts were characterized by powder X-ray diffraction (XRD) employing a scanning rate of 10°/min in a 2θ range from 10° to 70°, in a Bruker D8 Advance diffractometer using monochromatized CuKα radiation (λ = 1.5406 Å). The crystalline average size (d DRX) was assessed using calculation using the Debye–Scherrer equation [20–22] equation as follows Eq. (1):

$$d_{\text{DRX} } = \frac{0.9 \lambda }{\beta \sin \theta }$$
(1)

where \(\beta = \sqrt {(\text{FWHM} )^2 - (0.3)^2 }\) and λ is the X-ray wavelength (1.5406 Å). FWHM is the full-width at half maximum and θ is the Bragg angle. FWHM was calculated from the peak having highest intensity in all the samples. The lattice constants of the samples calculated from their corresponding XRD pattern data are obtained by full proof of program. The crystallite sizes of the pure nanoparticles were deduced from the XRD patterns by calculation of the Scherrer equation.

The morphologies of the samples were observed by scanning electron microscopy (SEM), which were taken on a S4800 Field Emission SEM (FESEM, Hitachi, Japan), using an accelerating voltage of 15 kV. Thermogravimetric analysis coupled with mass (TG-SM) was performed with a Setaram Instrument, at heating rate of 10 °C/min, a temperature range from 25 to 800 °C, in air gas purge of 30 ml/min with a sample weight of 22.4 mg.

Sorption study

Adsorption kinetics experiments were carried out as a single-stage batch test using a magnetically stirrer at 298 K using 250 mL beaker containing 100 mL different concentrations of dye solutions and doses of sorbent. The initial pH of dye solutions was adjusted at 7 by HCl and NaOH solutions using digital pH-meter using HANNA HI 83141. At given intervals, 5 mL aliquots were collected, centrifuged using EBA-Hetlich centrifuge at 3500 rpm for 15 min, and then filtered to remove the catalyst particles for analysis. The filtrates were finally monitored using a UV–Vis spectrophotometer using (UV–Vis Spectrometer Shimadzu UV mini-1240), in the λ range from 200 to 800 nm, using 1 cm optical pathway cells and computing from the calibration curves. The experiments were done by varying the contact time (0–60 min), concentration of dye solution (20–50 mg/L) and amount of adsorbent (0.375–1 g/L).

Isotherm studies

Adsorption experiments were carried out as a single-stage batch test using a magnetically stirrer. A suspension containing 0.1 g of adsorbent sample was mixed with a 100 mL aqueous solution of dye at a known initial concentration and initial pH in a flask. The initial pH values of the solutions were previous adjusted to 7. Aliquots of the solution were withdrawn at a predetermined time intervals and were centrifuged at 3500 rpm for 15 min to remove any adsorbent particles. Dye concentrations in the supernatant solutions were subsequently estimated by measuring absorbance at maximum wavelength of dye by spectrophotometer. The adsorption tests were continued until the equilibrium concentration was reached. The adsorption capacity of CR dye was researched over a range of concentration from 10 to 50 mg/L.

The adsorption capacity Q (mg/g) was calculated based on a mass balance equation as given below Eq. (2):

$$Q({\text{mg} /\text{g} }) = \left[{\frac{{({C_\text{e} - C_\text{t} })}}{m}}\right]v$$
(2)

The removal efficiency is expressed as follows Eq. (3):

$$\eta (\% ) = \left[{\frac{{({C_i - C_f })}}{C_i }}\right]\; \times \;100$$
(3)

where Q is the adsorption capacity of the adsorbate (mg/g), m is the weight of adsorbent (g), v is the volume of solution (L), and Co (mg/L) and Ce (mg/L) are initial and equilibrium concentration of adsorbate in solution, respectively.

Results and discussions

TG-MS analysis

TGA was used to clarify the appropriate heat treatment temperature for the tin complex. Coupling a mass spectrometer (MS) to a thermogravimetric analysis (TG) allows evolved gases to be analyzed and identified giving this additional valuable information. Figure 2, shows TG-SM curves of the SnO2-80 sample heated up to T = 800 °C. The TG curve shows three well defined regions of weight loss. The first mass loss involved the dehydration of two H2O molecules and the formation of insoluble SnC2O4 crystals occurs during the heating from 25 °C to T = 80 °C. Tin oxalate (SnC2O4) is stable until 250 °C and will be transformed completely into SnO2 at 330 °C as shown in the region of second mass loss. In this step, the organic ligand and other residues were continuously oxidized by heating from 250° to 330 °C. The second sequential weight loss displayed an even rapid and was found to be 50 %. Hardly any further weight loss in the TG curve can be observed at temperatures above 330 °C, indicating the completion of reaction as shown in the third sequential weight loss. The dehydration of hydroxide precursor and removal of organics in the form of oxides of carbon, the most likely dioxide of carbon by heating from T = 270 to T = 450 °C which was characterized at the MS curves by the highest intense peak at T = 380 °C and the lowest intense peak at T = 350 °C, respectively. As shown in Fig. 2, the chemical reaction finishes at about 380 °C, resulting in the formation of SnO2 powder [13]. Based on the thermal analysis results mentioned above, T = 450 °C was selected as appropriate calcination temperature for the precursors.

Fig. 2
figure 2

Thermogravimetric analysis (TGA) coupled with mass spectroscopy (MS) of the SnO2-80 precursor nanostructures

Full size image

XRD analysis

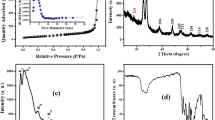
The XRD patterns of the nanostructured SnO2 are shown in Figs. 3 and 4. Diffraction peaks SnO2-80 sample (Fig. 3) was indexed as the pure monoclinic structure of tin oxalate (SnC2O4) lattice constant a = 10.3708 Å et b = 5.5035 Å and c = 8.7829 Å (which is in good agreement with standard value (JCPDS file No. 22-496). Diffraction peaks of SnO2-com (Fig. 4a) at 2θ of 26.63°, 33.73°,37.94°, and 51.79° can be indexed as the (110), (101), (200), and (211) planes of tetragonal rutile-like SnO2 [Cassiterite, Joint Committee on Powder Diffraction Standards (JCPDS) card No. 41-1445, space group: P42/mnm, lattice constant a = 4.7373(2) Å et b = 3.1865 (3) Å]. The relative intensities of (101) and (110) peaks are the largest. No characteristic peaks of impurities were observed, indicating the high purity of the product. The SnO2-450 and (Fig. 4c) and SnO2-650 (Fig. 4b) samples were also perfectly indexed as the pure tetragonal rutile structure of stannic oxide. The low index (110) face is the thermodynamically most-stable bulk termination in oxides and has the lowest surface energy [14]. It means that SnO2 prefer to grow along the [110] direction, forming the SnO2 nanostructure. The lattice constant of nanoparticle samples calculated from their corresponding XRD pattern data are obtained by full proof program were found to be a = 4.743(2) Å and b = 3.189 (2) Å for SnO2-450 sample, a = 4.758 (2) Å and b = 3.1875 (8) Å for SnO2-650 sample. Here, we observe that the XRD patterns in the 2θ range from 20° to 41° (Fig. 5) show that the SnO2-450 and SnO2-650 samples exhibit broadened peaks with a little shift toward lower intensities. Based on the Scherrer equation, the crystallite size of a sample is inversely proportional to the full-width-half-maximum (FWHM), indicating that a broader peak represents smaller crystallite size [23]. Thus, the higher temperature promotes the crystallinity and a consequent broadening of the diffraction peaks of the as-synthesized nanoparticles. The highest broadening of the diffraction peaks is observed for SnO2-450 sample. The crystallite sizes of SnO2-com, SnO2-450 and SnO2-650 samples deduced from the XRD patterns by calculation of the Scherrer equation showed that crystalline size, dXRD were found to be 50, 13 and 23 nm, respectively. The crystallographic parameters obtained on the SnO2 nanostructure powders given in Table 2 show that the calcination temperature did significantly decrease the crystallite size (increase the surface area) of the material SnO2. At 80 and 450 °C, an increase in the calcination temperature caused a remarkable decline of the crystallite size, which was not the case at 650 °C where the relatively higher calcination temperature significantly improved the crystallite size from 13 to 23 nm, this can be explained by the fact that at the thermal activation at 650 °C, the material particles became so finer, reducing the porosity of the surface and hence compacting it to generate a lower surface area. A previous study of [24] reported on the synthesis of the submicron tin oxide (SnO2) from tin(II) chloride and oxalic acid in air. It was found that the spherical particles of a very consistent diameter of 75 nm. For the SnO2 sample synthesized via the modified polyacrylamide gel route, in a recent published study [25] reported a calculated crystallite size of the sample prepared by using oxalic acid as the chelating agent at 118 nm. Another study on the synthesis of the nanoparticles tin oxide (SnO2) using citric acid as the chelating agent at 15 nm [26]. Therefore, our values are much lower than the reported data.

Fig. 3
figure 3

XRD pattern of tin oxalate SnC2O4 (denoted as SnO2-80) nanoparticles

Full size image
Fig. 4
figure 4

XRD patterns of SnO2-com (a), SnO2-450 (b) and SnO2-650 (c) nanoparticles

Full size image
Fig. 5
figure 5

XRD patterns of SnO2-com (blue color), SnO2-450 (red color) and SnO2-650 (green color) nanoparticles in the 2θ range from 20° to 41°

Full size image
Table 2 Crystallographic parameters of the as-synthesized SnO2 nanoparticles
Full size table

SEM analysis

Figure 6, illustrates typical SEM images of the as-synthesized tin oxides compared to SnO2-com samples. The SnO2-com morphologies consisted of large spherical aggregates of smaller individual nanostructures, as shown in Fig. 6a. Figure 6b illustrates typical high-resolution SEM image of SnO2-com sample to further show the details of the nanostructure. As seen in Fig. 6b, it clearly SEM analysis (Fig. 6b) shows two different spherical-shaped nanostructures on the SnO2 surfaces, which can be assigned to SnO2 with a particle size in the range of 0.1 µM and SnO with approximately 0.2 µm dimensions. Compared to SnO2-com, the morphology of SnO2-80 (Fig. 6c) consisted of mixtures of individual and intergrowths of elongated prisms, with a particle size in the range of 3–10 µM. Figure 6d, e, display the SEM images of SnO2-450 and SnO2-650 samples, revealing that the nanostructures consisted of a foamed body, which resulted from the gas release during decomposition. Previous published study [27] reported on the oxidation of VOC2O4 to V2O3. It was suggested that the reaction gases form a shell around the oxide particles during calcination, which can limit agglomeration. As the calcinations temperatures were increased up to 450 °C, the aggregation of the particles becomes more dominant. This can be attributed to the higher solubility and collision between particles. A strong degree of the foamed nanostructures with size about 750–3 µm was observed in SnO2-650 sample, which agrees with the XRD results. The different morphology reveals the key role of individual the oxalate acid chelating agent in controlling the nucleation and crystal orientation.

Fig. 6
figure 6

SEM images of SnO2: a low-resolution of SnO2-com, b high-resolution of SnO2-com, c SnO2-80 (SnC2O4), d SnO2-450 and e SnO2-650 nanoparticles

Full size image

Removal properties of CR

Effect of contact time

Figure 7 illustrates the effect of time on the removal of Congo red (CR) dye on SnO2-80, SnO2-450 and SnO2-com samples. The adsorption of this dye is fast in the first 10–30 min, and then gradually slows until equilibrium is reached. The equilibrium time obtained is basically depends on the nature of the explored material. As displayed in Table 3, the sorption efficiency of CR over the SnO2-80 nanoparticles was more than 84.41 % after 60 min of contact time, which was approximately 2 times as much as that of SnO2-450 (50.05 %) and was slight equal to SnO2-com (83.33 %). The obviously enhanced sorption efficiency of SnO2-80 catalyst was primarily caused by the balance of the high crystallinity and the large surface area for adsorbing substrates, in agreement with XRD and SEM results. However, these requirements are in general conflict with each other, because the crystallinity increases with the heat treatment temperature, while the surface area decreases. These data indicated that the removal of CR was not related to the available surface area; the SnO2-80 nanoparticles exhibited a lower surface area, but it had higher adsorption efficiency.

Fig. 7
figure 7

Adsorption kinetic for CR adsorption on SnO2-80, SnO2-450 and SnO2-com nanoparticles samples [(CR) = 20 mg/L, (m/v) = 0.5 g/L, pH 7, T = 298 K and contact time of 60 min]

Full size image
Table 3 Adsorption efficiency for CR adsorption of SnO2-80, SnO2-450 and SnO2-com nanoparticles samples [(CR) = 20 mg/L, (m/v) = 0.5 g/L, pH 7, T = 298 K and contact time of 60 min]
Full size table

This highlights that the adsorption of anionic dye, although believed to be primary an electrostatic interaction between the Sn2+ center and the electron rich nitrogen atoms of CR moiety, is rather complicated by many factors other than the surface characteristics of the adsorbent, such as dye–dye interaction.

For the SnO2-450 sample, the thermal activation at 450 °C, the material particles became so finer (high structure crystallinity), reducing the porosity of the surface and hence compacting it to generate a lower surface area for absorbing substrates, and therefore decreasing the number of active sites and the attraction between the dye and the SnO2-450 surface [28]. Hence the sequential sorption activity was as follow:

$$\boldsymbol{\upeta}_{\text{CR} /\text{SnO}_2 - 80} > \boldsymbol{\upeta}_{\text{CR} /\text{SnO}_2 - \text{com} } > \boldsymbol{\upeta}_{\text{CR} /\text{SnO}_2 - 450}$$

Effects of initial dye concentration

The effects of initial dye concentration as a function of contact time were conducted in the range of 0–60 min. The results (Fig. 8) indicated that the process is found to be very rapid initially, and the equilibrium is achieved within 60 min. As illustrated in Fig. 8, the adsorption efficiency of SnO2-80 nanoparticles decreased from 84.41 % (33.766 mg/g) to 46.59 % (46.595 mg/g) when the initial concentration of dye was increased from 20 to 50 mg/L, respectively. Initial concentration provides an important driving force to overcome all mass transfer resistances of the dye between the aqueous and solid phases. Decrease in adsorption efficiency with initial concentration of dye in due to the dye agglomeration and the reduction of the thermal mobility of the adsorbed aggregates. Hence, a lower initial concentration of dye may enhance the process. So, for CR dye, the initial dye concentration of 20 mg/L is selected for subsequent experiments.

Fig. 8
figure 8

Adsorption kinetic for CR adsorption onto SnO2-80 nanoparticles at various initial concentration of the dye solution [(m/v) = 0.5 g/L, pH 7, T = 298 K and contact time of 60 min]

Full size image

Effects of adsorbent dose

The effect of adsorbent dose of SnO2-80 nanoparticles on the adsorption of CR dye is conducted over a range of adsorbent doses of 0.375 to 1 g/L. As elucidated in Fig. 9, the efficiency of CR adsorbed raised from 85.56 % (114.077 mg/g) to 93.77 % (93.766 mg/g) when the adsorbent dose increases from 0.375 to 0.5 g/L. This increase in adsorption efficiency with the adsorbent dose can be assigned to the increased surface area and the availability of more adsorption active sites. Further increase in the adsorbent dose beyond of 0.5 g/L, the adsorption efficiency gradually decreased, almost reaching 85.45 % (42.727 mg/g) at 1 g/L, due to overlapping of adsorption sites as a result of overcrowding of adsorbent. The maximum adsorbent dose of SnO2-80 nanoparticles was found to be 0.5 g/L.

Fig. 9
figure 9

Adsorption kinetic for CR adsorption onto SnO2-80 nanoparticles at various adsorbent doses of SnO2-80 sample [(CR) = 20 mg/L, pH 7, T = 298 K and contact time of 60 min]

Full size image

The adsorption kinetics of CR dye on SnO2-80 nanoparticles at different initial concentration and adsorbent doses, illustrated in Figs. 8 and 9, respectively, were treated with a pseudo-first-order and pseudo-second-order models, and the best fit model was selected according to the linear regression correlation coefficient, R2 value. The pseudo-first-order model [29] is generally expressed as (Eq. (4)):

$$\log (Q_e - Q_t ) = \log Q_e + \frac{K_1 }{2303}t$$
(4)

where Q e and Q t (both in mg/g) are the amount of dye adsorbed per unit weight of adsorbent at equilibrium and at any time t, respectively. K 1 is pseudo-first order rate constant (min−1). The adsorption rate constants (K 1) and the equilibrium adsorption capacity (Q e ), were calculated experimentally from the linear plots of log (Q e – Q t ) versus t at different concentrations of CR (Fig. 10) and various adsorbent doses of SnO2-80 (Fig. 12) are summarized in Tables 4 and 5, respectively.

Fig. 10
figure 10

Pseudo-first-order kinetic for CR adsorption onto SnO2-80 nanoparticles at various initial concentration of the dye solution [(m/v) = 0.5 g/L, pH 7, T = 298 K and contact time of 60 min]

Full size image
Fig. 11
figure 11

Pseudo-second-order kinetic for CR adsorption onto SnO2-80 nanoparticles at various initial concentration of the dye solution [(m/v) = 0.5 g/L, pH 7, T = 298 K and contact time of 60 min]

Full size image
Fig. 12
figure 12

Pseudo-first-order kinetic for CR adsorption at various adsorbent doses of SnO2-80 nanoparticles [(CR) = 50 mg/L, pH 7, T = 298 K and contact time of 60 min]

Full size image
Table 4 Adsorption kinetic parameters for dyes adsorption onto SnO2-80 nanoparticles at various initial concentration of the dye solution [(m/v) = 0.5 g/L, pH 7, T = 298 K and contact time of 60 min)
Full size table
Table 5 Adsorption kinetic parameters for dye adsorption onto SnO2-80 nanoparticles at various adsorbent doses of SnO2-80 sample [(CR) = 50 mg/L, pH 7, T = 298 K and contact time of 60 min]
Full size table

The usual way to validate a model is to consider the goodness-of-fit using the linear regression coefficients, R 2. However, using only the linear regression method may not be appropriate for comparing the goodness of fit of kinetic models. This is because an occurrence of the inherent bias resulting from linearization may affect the deduction. Therefore, in this study in addition to the linear regression analysis, the experimental data were tested with sum-of-square error (F error) [30] to determine the best fitting kinetic model. The error function is given by (Eq. (5)):

$$F_{\text{error} } = \sqrt[2]{\sum{\frac{{({ Q_{\text{e} ,\text{calc} } - Q_{\text{e} , \exp } })^2 }}{ N}}}$$
(5)

where Q e,exp is the experimentally determined sorption capacity; Q e,calc is the theoretical sorption capacity from the different kinetic models and N is the number of data points.

The results show that the values of R 2 ranged from 0.81 to 0.92 for initial concentrations of CR of 20, 40, and 50 mg/L and from 0.81 to 0.99 for adsorbent doses of 0.37, 0.5 and 1 g/L, respectively. Furthermore, the experimental (Q e,exp) data do not agree well with the calculated values (Q e,cal.), as shown in Tables 4 and 5. The model is not able to describe the experimental data properly because of the poor linear correlation and high F error values (Tables 4, 5). All these observations show that the adsorption of CR onto SnO2-80 does not follow first-order kinetics.

The pseudo-second-order model [31] is represented as (Eq. (6)):

$$\frac{t}{Q_t } = \frac{1}{{Q_\text{e}^2 K_2 }} + \frac{1}{{Q_\text{e} }}t$$
(6)

where K 2 is the pseudo-second-order constants (g/mg min). The initial adsorption rate, h (mg/g min−1), as t → 0 can be defined as (Eq. (7)):

$$h = K_2 Q_\text{e}^2$$
(7)

The equilibrium adsorption capacity (Q e), and the pseudo-second-order constant (K 2) can be determined experimentally from the slope and intercept of plots of t/Q t versus t, respectively, at different concentrations of R (Fig. 11) and various adsorbent doses of SnO2-80 (Fig. 13).

Fig. 13
figure 13

Pseudo-second-order kinetic for CR adsorption onto SnO2-80 nanoparticles at various adsorbent doses of SnO2-80 sample [(CR) = 50 mg/L, pH 7, T = 298 K and contact time of 60 min]

Full size image

The R 2 values different CR dye concentrations and SnO2-80 adsorbent doses of the linear portions are very high; and are close or equal to unity (0.99–1), which strongly suggests that adsorption of the CR follow the pseudo-second-order kinetic model the wherein the overall rate of the adsorption process was controlled by chemisorptions which involved valency forces through electrons sharing between the adsorbent and adsorbate and higher adsorption energy. There is also a very good consistency between the calculated values (Q e,cal.) and the experimental data (Q e,exp) and the low values of its F error values, as displayed in Tables 4 and 5.

Adsorption isotherm

To describe the adsorption behavior of Congo red dye by SnO2-80 nanoparticle adsorbent, we have studied adsorption isotherms. Inset in Fig. 14 shows equilibrium adsorption curves of CR on SnO2-80 nanoparticles at room temperature. The adsorption of CR forms a typical Langmuir-type isotherm according to Giles classification system [32]. The adsorption capacity increased sharply at lower adsorption equilibrium dye concentration and thereafter the increase is gradual with an increase of equilibrium dye concentration. The maximum adsorption capacity of SnO2-80 for CR was found to be 45.49 mg/g. Due to their widespread applications, the Langmuir [33] and Freundlich [34] isotherm models were applied to assess the performance of the adsorption process of CR dye onto SnO2-80 nanoparticles.

Fig. 14
figure 14

Adsorption isotherm of dye adsorbed onto SnO2-80 nanoparticles [(CR) = 20–50 mg/L, pH 7, T = 298 K and contact time of 60 min]

Full size image

To evaluate which model was best suited to describe these processes, and the error function (F error) were analyzed; a lower result from the error function indicated a smaller difference between adsorption capacity calculated by the model (Q calc) and the experimental (Q exp). F error can be expressed according to Eq. (8) [35]:

$$F_{\text{error} } = \mathop \sum \limits_{i = 0}^P ({\frac{{Q_{i,\text{calc} } - Q_{i,\exp } }}{{Q_{i,\exp } }}})^2$$
(8)

where Q i,calc is a value of Q predicted by the fitted model; Q i,exp is a value of q measured experimentally; i indicates the values of the initial dye concentration of the experiments (20, 30, 40 and 50 mg/L); and P is the number of experiments performed.

The Freundlich isotherm is an empiric equation employed to describe heterogenous systems. The logarithmic form of the Freundlich equation Eq. (9) is:

$$\text{Ln} Q_\text{e} = \text{Ln} K_\text{F} + \frac{1}{n}\text{Ln} C_\text{e}$$
(9)

where K F and 1/n are Freundlich adsorption isotherm constants (L/mg), being indicative of the extent of the adsorption and the degree of nonlinearity between solution concentration and adsorption [the adsorption process to be linear (n = 1), chemical (n < 1) and favorable physical process (n > 1)], respectively. Therefore K F and 1/n were calculated from the plots of LnQ e against LnC e. These values, along with r and F error, are shown in Table 6.

Table 6 Isotherm parameters of dye adsorbed onto SnO2-80 nanoparticles for CR [(CR) = 50 mg/L, pH 7, T = 298 K and contact time of 60 min]
Full size table

The Langmuir adsorption isotherm assumes that adsorption takes place at specific homogeneous sites within the adsorbent and has found successful application in many adsorption processes of monolayer adsorption. The linear form of the Langmuir isotherm equation is represented by the following equation Eq. (10):

$$\frac{{C_\text{e} }}{{Q_\text{e} }} = \frac{1}{{K_\text{L} Q_{\hbox{max} } }} + \frac{{C_\text{e} }}{{Q_{\hbox{max} } }}$$
(10)

where Q max (mg/g) is the maximum amount of the dye per unit weight of SnO2-80 nanoparticles to form a complete monolayer coverage on the surface bound at high equilibrium dye concentration C e (mg/L) and K L (L/g) is the Langmuir constant related to the affinity of binding sites. A plot of C e/Q e versus C e leads to a straight line with the slope of 1/Q max and an intercept of 1/Q max K L.

The essential characteristics of Langmuir isotherm can be expressed by a dimensionless constant called equilibrium parameter R L that is defined by the following equation Eq. (11):

$$R_\text{L} = \frac{1}{{(1 - K_\text{L} C_0 )}}$$
(11)

where K L and C 0 are the same as defined before. The value of R L calculated from the above expression. The nature of the adsorption process to be either unfavorable (R L > 1), linear (R L = 1), favourable (0 < R L < 1) or irreversible (R L = 0).

Figures 15 and 16, show the plot of the experimental data based on Langmuir and Freundlich isotherm models, respectively. Table 2 depicts the calculated values of Langmuir and Freundlich model’s parameters. Based on the regression coefficients (R 2) of the linearized form of both equations and their errors function (F error), the Langmuir model yields a better fit for the experimental equilibrium adsorption data than the Freundlich model. The high fit to the Langmuir model suggests that the adsorption is limited with monolayer coverage. All the R L-values for the adsorption of CR onto SnO2-80 nanoparticles are in the range of 0–1, suggesting that the adsorption is favorable under the conditions proposed by the Langmuir model. The R 2 value is greater than 0.93, its F error is lower than 0.27, thus, lower than the one obtained for the Freundlich model. The maximum adsorption capacity of SnO2-80 nanoparticles for CR calculated from the Langmuir isotherm model was 48.31 mg/g. Thus, these data suggest that Langmuir isotherm model was suitably fitted [36].

Fig. 15
figure 15

Langmuir isotherm linearized model [(CR) = 20–50 mg/L, pH 7, T = 298 K and contact time of 60 min]

Full size image
Fig. 16
figure 16

Freundlich isotherm linearized model [(CR) = 20–50 mg/L, pH 7, T = 298 K and contact time of 60 min]

Full size image

According to Langmuir isotherm model, the maximum adsorption capacity (O exp) for the adsorption of CR on SnO2 is found to be 48.31 mg/g. The maximum adsorption capacity (O max) for the adsorption of CR on SnO2 nanoparticles compared to other adsorbents is listed in Table 7. It can be seen that adsorption capacity varies and depends on the properties of the individual adsorbent, the extent of surface/surface modification, the initial concentration of the adsorbate, range of molecular size fraction of adsorbate and degree of ionization per unit weight of adsorbate. It is observed also that the prepared SnO2-80 nanoparticles are an efficient adsorbent for adsorption of Congo red from aqueous solution.

Table 7 Comparison of Congo red adsorption capacities of various adsorbents
Full size table

Discussion of mechanism

The surface chemistry of the adsorbents plays a major role in the adsorption. The particles of SnC2O4 are roughly in elongated prisms shape with average particle size of 10 µm. The oxygen content of the surface is about 80 % giving a O (at%)/Sn (at%) ration of approximately 4:1, the stoichiometry of SnC2O4. The large number and array of different functional groups on the SnC2O4 surfaces (e.g., oxygenic and carbonyl) implied the existence of many types of adsorbent–solute interaction. As shown in Fig. 17, the adsorption of the azo dye on SnC2O4 layer is favored, mainly due to the electrostatic interaction between the Sn2+ center and the electron rich nitrogen atoms of CR moiety [75]. Additionally, SnC2O4 nanoparticles can capture more dye molecules via the formation of hydrogen bond [68].

Fig. 17
figure 17

Schematic illustration of CR dye removal process

Full size image

Conclusion

In Summary, the nanoparticles SnO2 have been successfully synthesized via a sol-gel method. The as-prepared SnO2 was characterized using a number of techniques such as thermogravimetric analysis coupled with mass spectroscopy (TG-SM), X-ray diffraction (XRD) and scanning electron microscope (SEM). Batch experiments were carried out to study the adsorption kinetics of Congo red azo dye, as probe pollutant, on SnO2. The effect of varying parameters such as contact time, initial dye concentration and adsorbent dose on the adsorption process was investigated. The results showed that the SnO2 catalysts have high crystallinity with tetragonal rutile structure and average particle size about 13–23 nm. The untreated sample SnO2-80 exhibited high efficiency (84.41 %) after 60 min of exposure time, which was 2 times as much as that of SnO2-450 sample. Experimental kinetic data were satisfactory correlated with the pseudo-second-order kinetic model, with highest correlation coefficients (R 2 ≥ 0.99). The formation of hydrogen bond and the electrostatic interaction between the Sn2+ center and the electron rich nitrogen atoms of CR moiety were believed to be was the main adsorption mechanism. Regarding the adsorption equilibrium, the experimental results suggest that the Langmuir model was applicable. The obtained SnO2 is a promising candidate for potential application in organic pollutant uptake from contaminated water sources.