1 Introduction

The design and analysis of reinforced concrete members subjected to shear may be performed taking into consideration different strategies reported in the literature, among several others (ASCE-ACE Committee 445 on Shear and Torsion 1998; Hernández-Díaz and Gil-Martín 2012; Jeong and Kim 2014; Mofidi and Chaallal 2014). One of the most widely known is the so-called Modified Compression Field Theory (MCFT) (Vecchio and Collins 1986). In the MCFT, the stress–strain relationship for the steel reinforcement is assumed to be elastic-perfectly plastic, being the Young’s modulus constant up to the yield strength (f y ) and then zero upon yielding at the crack location. To allow new increments of shear force, MCFT introduces the notion of local shear stress, and as a consequence, requires the check of equilibrium conditions for local shear stresses at the crack location in order to ensure that the steel stress does not exceed the steel yield strength.

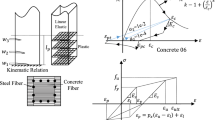
A few years ago, Gil-Martín et al. (2009) proposed a new steel constitutive model leading to the Refined Compression Field Theory (RCFT). In the line of a few other shear theories, such as the Rotating Angle-Softened Truss Model (RA-STM, Belarbi and Hsu 1994), the RCFT proposes a stress–strain relationship for the reinforcing bars stiffened by concrete (“embedded bar model”); the novelty is that the embedded bar stress–strain relationship is obtained imposing equilibrium on the tension stiffening effect; so new formulation for the steel model would no longer be needed (compared with RA-STM) and the crack check can be avoided (compared with MCFT). According to Gil-Martín et al. (2009), from equilibrium of forces between a cracked section and a generis section (see Fig. 1a), the RCFT predicts the average stress (along the bar between cracks) of an embedded bar as a function of the average strain (i.e., measured on certain length including several cracks):

$$\begin{aligned} \sigma_{s,av} &= \left\{ {\begin{array}{*{20}c} {f_{y\,} - \,\frac{{A_{c} }}{{A_{s} }}\frac{{f_{ct} }}{{1 + \sqrt {3.6M\varepsilon_{s} } }}} & \quad{if\,\,\varepsilon_{s} \ge \varepsilon_{{max} } } \\ {E_{s} \varepsilon_{s} } & \quad{if\,\,\varepsilon_{s} < \varepsilon_{{max} } } \\ \end{array} } \right. \hfill \\ {with}&\hfill\\ \varepsilon_{{max} } \, &= \,\frac{{f_{y\,} }}{{E_{s} }}\,\, - \,\,\frac{{\frac{{f_{ct} }}{{1 + \sqrt {3.6M\,\varepsilon_{{max} } } }}}}{{E_{s} A_{s} }}A_{c} \hfill \\ M &= \,\frac{{A_{c} }}{{\sum {\phi \pi } }}\, \hfill \\ \end{aligned} $$
(1)

where σ s,av is the average tensile stress in steel (for longitudinal or transverse reinforcement), A s is the cross section of steel bar (longitudinal or transverse), ε s is the average tensile strain in steel and concrete, f ct is the tensile strength of concrete, E s is the elastic modulus of reinforcement, ε max is the apparent yield strain (or average tensile strain when first yielding occurs at the crack location, Fig. 1) and A c is the area of concrete bonded to the bar. Technical codes (e.g., EHE 2008) usually define A c as a value equal to the rectangular area (tributary to and surrounding the bar) over a distance not exceeding 7.5Ø from the center of the bar (Fig. 1b), and Ø is the diameter of the bar. Hereafter, we refer to A c as the prescribed tension stiffening area. In Eq. (1) the embedded bar stress–strain relationship is established for the concrete tension stiffening model proposed by Bentz (2005).

Fig. 1
figure 1

a Steel embedded bar in tension (adapted from Gil-Martín et al. 2009); b Area A c of concrete bonded to the bar (according to EHE-08).

Full size image

Numerical results obtained from RCFT for different tested specimens (Gil-Martín et al. 2009; Palermo et al. 2013) show a better fitting of the experimental results, in particular near the peak point in the shear response curve, where the MCFT significantly deviates from the experimental evidences. Nevertheless, it can be proved that when the prescribed tension stiffening area (A c ) is adopted, for certain specimens (specifically those with high values of the ratio f ct /ρ, being ρ the reinforcement ratio) it is not possible to obtain a positive real solution for the apparent yield strain (ε max ) defined in Eq. (1). If all terms in the expression of the apparent yield strain are moved to the right hand side, the following function G is obtained:

$$ \varepsilon_{{max} } \, = \,\frac{{f_{y\,} }}{{E_{s} }}\,\, - \,\,\frac{{\frac{{f_{ct} }}{{1 + \sqrt {3.6M\,\varepsilon_{{max} } } }}}}{{E_{s} A_{s} }}A_{c}^{\prime} \to G[f_{ct} ,\varepsilon_{{max} } ] = \left( {\varepsilon_{y} - \varepsilon_{{max} } } \right) - \frac{{\frac{{A_{c}^{\prime} f_{ct} }}{{1 + \sqrt {3.6M\varepsilon_{max} } }}}}{{E_{s} A_{s} }} $$
(2)

where ε y is the strain corresponding to f y (i.e., ε y  = f y /E s ). A new variable, \( A_{c}^{\prime} \), has been introduced in Eq. (2) in order to discuss the solvability of this equation in terms of the ratio \( A_{c}^{\prime} /A_{c}^{{}} \). To illustrate the effect of the tension stiffening area in the solvability of the RCFT model, the top longitudinal reinforcement of a beam (specimen H75/2) tested in shear by Cladera in 2002 has been considered. The top longitudinal bar diameter is 8 mm, the side cover is 25 mm, the prescribed tension stiffening area (according to EHE) is 9025 mm2, the tensile strength of concrete (f ct ) is 4.5 MPa and the yield stress of steel (f y ) is 530 MPa. The function G [f ct , ε max ] has been represented in Fig. 2 for different values of \( A_{c}^{\prime} \), resulting in a set of curves. For this specimen, the apparent yield strain (ε max ) corresponds to the intersection points of these curves with the abscissa f ct  = 4.50 MPa.

Fig. 2
figure 2

Specimen H 75/2 (Cladera Bohigas 2002): solvability graphical analysis for apparent yield strain (ε max ) in the top longitudinal reinforcement.

Full size image

The interval adopted for the strength f ct in Fig. 2 coincides with the range established for this parameter by EC-2 (2002). It can be seen that, for high values of \( A_{c}^{\prime} \) (like \( A_{c}^{\prime} = 0.7A_{c} \) and \( A_{c}^{\prime} = 0.9A_{c} \)), the curve G [f ct , ε max ] = 0 presents a knee that breaks the bijection between f ct and ε max (problem of uniqueness), or even, no solutions exists for ε max (problem of existence), as it occurs by taking \( A_{c}^{\prime} = A_{c} \) in this specimen. In relation to the problem of uniqueness, by continuity and taking into account that ε max  = ε y when \( A_{c}^{\prime} = 0 \) (cf. Gil-Martín et al. 2009), the actual value of ε max is that of the solution closest to the yield strain ε y , that is, the greatest one of the two positive real solutions of Eq. (2). However, the absence of solution in the steel constitutive model proposed by RCFT indicates that the equilibrium of internal forces along the cracked member (see Fig. 1) is not verified, and therefore, the stress–strain relationship for the steel must be corrected.

2 Fixing the Tension Stiffening Area

Hereafter, assume f ct is a parameter, and abusing the notation, denote also by G [ε max , \( A_{c}^{\prime} \)] the above mentioned bivariate function G [f ct , ε max ]. In Fig. 3a the function G [ε max , \( A_{c}^{\prime} \)] has been represented for three values of \( A_{c}^{\prime} \); this figure shows that the equation G [ε max , \( A_{c}^{\prime} \)] = 0 ceases to have positive real solutions when the value of \( A_{c}^{\prime} \) is greater than the one that makes the graphic of G tangent to the positive part of the abscise axis. This turns out to happen when both functions G[ε max , \( A_{c}^{\prime} \)] and \( G^{\prime } \) [ε max , \( A_{c}^{\prime} \)] vanish simultaneously, where:

Fig. 3
figure 3

Parameters of RC section: f y  = 530 MPa, f ct  = 4.50 MPa, A s  = 50.27 mm2 (1 Ø 8), A c  = 9025 mm2: a Function G[ε max ] for different values of \( A_{c}^{\prime} \); the equation G[ε max ] = 0 has no positive real solutions when \( A_{c}^{\prime} /A_{c} \) is greater than the limit value λ. b Effect of tension stiffening area over the embedded steel behavior model.

Full size image
$$ G^{\prime}[\varepsilon_{{max} } ,A_{c}^{\prime} ] = \frac{{\sqrt {3.6M} \, A_{c}^{\prime}f_{ct} }}{{2A_{s} E_{s} \left( {1 + \sqrt {3.6M\varepsilon_{{max} } } } \right)^{2} \sqrt {\varepsilon_{{max} } } }} - 1, \, \varepsilon_{{max} } > 0 $$
(3)

is the derivative of G[ε max , \( A_{c}^{\prime} \)]. Solving the system of equations {G[ε max , \( A_{c}^{\prime} \)] = 0, \( G^{\prime } \) [ε max , \( A_{c}^{\prime} \)] = 0} in the unknowns ε max and \( A_{c}^{\prime} \) , the positive real solution for the apparent yield strain is

$$ \varepsilon_{{max} } = \frac{{2 + 10.8M\varepsilon_{y} - 2\sqrt {1 + 10.8M\varepsilon_{y} } }}{32.4M}{ ,} $$

and it is solvable only when

$$ A_{c}^{\prime} = \frac{{A_{s} f_{y} }}{{f_{ct} }}\left( {\frac{2}{3} + \frac{{\sqrt {(1 + 10.8M\varepsilon_{y} )^{3} } - 1}}{{48.6M\varepsilon_{y} }}} \right) $$

This value of \( A_{c}^{\prime} \) is the greatest one for which G [ε max , \( A_{c}^{\prime} \)] = 0 has, at least, a positive real solution. Let us denote λ the factor:

$$ \lambda = \frac{{A_{s} f_{y} }}{{A_{c} f_{ct} }}\left( {\frac{2}{3} + \frac{{\sqrt {(1 + 10.8M\varepsilon_{y} )^{3} } - 1}}{{48.6M\varepsilon_{y} }}} \right) . $$
(4)

In a general sense, the factor λ represents the greatest portion of the tension stiffening area which may be taken in order to preserve the internal equilibrium of forces, in such a way that as concrete participation increases, the steel stress diminishes. According to this consideration, the effect of tension stiffening area over the embedded steel behavior model is illustrated in Fig. 3b for the case of specimen H75/2.

Several studies (Gil-Martín et al. 2009; Palermo et al. 2013; Hernández-Díaz 2012; Palermo et al. 2014) show the convenience of correcting the prescribed tension stiffening area in order to adjustment the shear response of reinforced concrete members, particularly for high shear strains, where the technical codes underestimate the concrete tension stiffening (Gil-Martín et al. 2009; Hernández-Díaz 2012). This strategy only can be performed for those values of \( A_{c}^{\prime} \) such that \( 0 \le A_{c}^{\prime} /A_{c}^{{}} \le \lambda \). In order to display the usefulness of the coefficient λ, a widely validated shear test (Abersman and Conte 1973), apud (Collins and Mitchell 1991; Hernández Montes and Gil-Martín 2014), has been considered; to this aim, the load-strain curve of the tested specimen has been predicted using the RCFT under two assumptions: (1) neglecting the contribution of the concrete tension stiffening area surrounding the reinforcement bars (i.e., \( A_{c}^{\prime} \) ≈ 0), and (2) considering the limit value of the tension stiffening area established by the coefficient λ. These two curves have been illustrated in Fig. 4 together the experimental shear response obtained in (Abersman and Conte 1973). As shown, the experimental results lie about halfway the shear curve corresponding to the assumption (1) and the limit curve corresponding to the coefficient λ; in particular, for a low-intermediate range of the shear strain, the limit tension stiffening area proposed in this work coincides approximately with the experimental response. In this sense, the factor λ establishes a feasible (solvable) search domain for the experimental adjustment of RCFT model using metaheuristic methods (cf. Hernández-Díaz 2012), what improves the computational effectiveness of this process.

Fig. 4
figure 4

Prestressed concrete beam CF1 (Abersman and Conte 1973): feasible search domain for the experimental adjustment of the RCFT model. (V shear force; ε t transverse strain).

Full size image

In the preceding results, the tension-stiffening curve proposed by Bentz has been assumed; however, the formulation of coefficient λ may be adapted to other tension stiffening models proposed in the literature (cf. Vecchio and Collins 1986; Palermo et al. 2013; Stramandinoli et al 2008; Hernández-Montes et al. 2013; Wu and Gilbert 2008) Recently, Hernández-Montes et al. (2013) proposed a tension stiffening curve, based on EC-2 formulation, which takes into account both the reinforcement ratio and the mechanic characteristics of the involved materials. Such expression is only valid until the reinforcement reaches the yield strain (ε y ) at any crack location. Once more, the apparent yield strain (ε max ) may be obtained from internal equilibrium; in this case, the above-defined function G adopts the following expression (see Eq. (13) at Carbonell-Márquez et al. 2014):

$$ G[\varepsilon_{{max} } ,\rho_{eff} ] = \left( {\varepsilon_{y} - \varepsilon_{{max} } } \right) - \frac{{\sqrt {\left( {\frac{{\rho_{eff} }}{2}E_{s} \varepsilon_{{max} } } \right)^{2} \,+\, f_{ct}^{2} \left( {1 + n\rho_{eff} } \right)} - \frac{{\rho_{eff} }}{2}E_{s} \varepsilon_{{max} } }}{{E_{s} \rho_{eff} }} $$
(5)

where n = E s /E c and ρ eff is the effective reinforcement ratio (\( \rho_{eff} = A_{s} /A^{\prime }_{c} \)). Equation (5) represents a monotonically decreasing function over the whole strain domain; therefore, in this case the value of \( A^{\prime }_{c} \) must be only constrained in order to avoid values of ε max lower than the average strain ε ct corresponding to the concrete tensile strength (f ct ), then the expression of coefficient λ is given by:

$$ \lambda = \frac{{\rho_{eff} }}{2}\left( {\frac{{\sqrt {f_{ct}^{2} n^{2} - 4f_{y} \left( {f_{ct} n - f_{y} } \right)} }}{{f_{ct} }} - n} \right) $$
(6)

3 Conclusions

A practical relationship is obtained between the reinforcement area (A s ), the tensile concrete strength (f ct ) and the yield stress (f y ) for a given value of the tension stiffening area (A c ). These four parameters are not independent, and three of them constrain the fourth one in order to preserve the internal equilibrium of a cracked member. Therefore, such relation must be satisfied in order to make operative the embedded steel constitutive model for every reinforced concrete section. Finally, this result is extensive to every structural system involving cracked embedded reinforcing bars.