1 Introduction

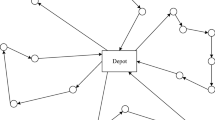
Traffic flow models have been developed and used to understand, describe and predict traffic flow since the beginning of the twentieth century. We present a review of traffic flow models following the historical lines of their development. Previous reviews focus on the, at that moment, current state-of-the-art and review the models on their current value (Papageorgiou 1998; Brackstone and McDonald 1999; Zhang 2001; Hoogendoorn and Bovy 2001b; Helbing 2001; Kerner 2009; Treiber and Kesting 2010; Treiber et al. 2010; Orosz et al. 2010; Wilson and Ward 2011; Bellomo and Dogbe 2011). We aim to take one step further back and give an historical overview of the highlights in traffic flow modeling. This approach shows better how traffic flow models have developed, and how different types of models are related to each other. Furthermore, it forms the basis of our next step in traffic flow modeling, using a multi-class approach (van Wageningen-Kessels et al. 2014; van Wageningen-Kessels 2013). To show the historical development of traffic flow models we introduce a model tree, see Fig. 1 and the Electronic Supplementary Material accessible via the publishers’ website (see link on the first page of this article).

Fig. 1
figure 1

Genealogical tree of traffic flow models showing four families and all their branches. For details of the families and branches we refer to Figs. 2, 8, 11 and 12. For a full-scale version of the model tree, we refer to the Electronic Supplementary Material accessible via the publishers’ website (see link on the first page of this article)

Full size image

All models in the tree have one common ancestor: the fundamental relation (or fundamental diagram). After the introduction of the fundamental relation in the 1930s, microscopic and macroscopic models were introduced simultaneously in the 1950s. The family of mesoscopic models is about a decade younger. The model tree shows that particularly over the last two decades: all families and branches have developed further, and many offshoots can be recognized.

The fundamental diagram relates the headways (front-to-front following distance) to vehicle velocity. How headways and velocities change over time (traffic dynamics) can be described by micro-, meso- or macroscopic models. On the one hand, microscopic models distinguish and trace the behavior of each individual vehicle. On the other hand, macroscopic models aggregate vehicles and traffic are described as a continuum. Mesoscopic models are categorized in between micro- and macroscopic models, as their aggregation level is between those of micro- and macroscopic models. Categorizing traffic flow models can be done according to other criteria such as whether the variables are continuous or discrete, the level of detail, stochastic or deterministic process representation, the scale of the application, type of model equations [(partial) differential equations, discrete equations] or the number of phases described by the model (Hoogendoorn and Bovy 2001b; Treiber and Kesting 2010; Treiber et al. 2010). Since the development of traffic flow models has followed largely the family lines of micro-, meso- and macrosopic models, we use this traditional categorization.

The outline of this article is as follows. We first discuss the fundamental relation in more detail, see Sect. 2. We then discuss each of the other three families: Sect. 3 presents microscopic models, Sect. 4 presents mesoscopic models, and Sect. 5 presents macroscopic models. Section 6 concludes this contribution with a discussion and future research suggestions. Each of the Sects. 2–5 contains figures with details of the model tree. We encourage the reader to view the full-scale model tree in the Electronic Supplementary Material accessible via the publishers’ website (see link on the first page of this article).

2 Fundamental diagram

Traffic flow models are based on the assumption that there is some relation between the distance between vehicles and their velocity, e.g., as in Fig. 3d. This relation between distance and velocity was first studied by Greenshields (1934) and called the fundamental relation (or fundamental diagram) later. Therefore, Greenshields is often regarded as the founder of traffic flow theory. The fundamental diagram family and its most important relations is shown in Fig. 2.

Fig. 2
figure 2

Details of the genealogical tree of traffic flow models showing the fundamental diagram family and its most important relations

Full size image

2.1 Shapes of the fundamental relation

Originally, Greenshields (1934) studied the relation between the variables spacing (\(s\), average distance between fronts of two consecutive vehicles) and velocity (\(v\)). However, the fundamental relation can also be expressed in other variables such as density (\(\rho\), average number of vehicles per unit length of road) and flow (\(q\), average number of vehicles per time unit), see Fig. 3.

Fig. 3
figure 3

Fundamental relations in different planes

Full size image
Fig. 4
figure 4

Different shapes of fundamental relations. Top fundamental relations in density–flow plane, bottom the same fundamental relations but in the density–velocity plane

Full size image

Greenshields (1934) proposed a fundamental relation that is linear in the spacing–velocity plane. However, his name has now been linked to the fundamental relation that he proposed 1 year later (Greenshields 1935). This fundamental relation is linear in the density–velocity plane and thus parabolic in the density–flow plane, see Fig. 4a, e. The model tree shows that since then, many other shapes of fundamental relations have been proposed. The Daganzo (1994) fundamental relation is probably the most widespread. It is bi-linear (triangular) in the density–flow plane, see Fig. 4b, f. Figure 4c, g shows the Smulders fundamental diagram (Smulders 1990), which is a combination of the previous two: it is parabolic for low densities and linear for high densities (parabolic–linear). Finally, Fig. 4d, h shows the Drake fundamental relation (Drake et al. 1967). For a more detailed overview of different shapes of fundamental relations we refer to Li (2008).

2.2 Scatter in the fundamental relation

Observed density–flow plots usually show wide scatter, see Fig. 5. Zhang (1999) and Laval (2011) argue that much of the scatter can be explained by non-equilibrium traffic conditions. Zhang defines traffic to be in equilibrium if over a sufficiently long time (\(t\)) and road length (space \(x\)) velocity and density do not change: \(\partial v / \partial t = 0\), \(\partial \rho / \partial t = 0\), \(\partial v / \partial x = 0\) and \(\partial \rho / \partial x = 0\). Only points in the scatter plot that satisfy these criteria can be used to fit the fundamental relation. This is then called the equilibrium fundamental relation. However, also in the equilibrium fundamental relation, scatter may exist. The other branches of the fundamental-relation family try to explain scatter in different ways.

Fig. 5
figure 5

Scatter in an observed density–flow plot (picture adapted from Treiber et al. 2006b)

Full size image
Fig. 6
figure 6

Fundamental ‘relations’ based on scatter in observations

Full size image

Edie (1961), Cassidy and Bertini (1999) explain part of the scatter with a capacity drop: just before the onset of congestion the outflow out of a bottleneck is higher than in congestion, see Fig. 6a. The capacity drop has been explained by a low acceleration rate of vehicles leaving congestion, while they decelerate at a high rate when entering congestion. This theory leads to fundamental relations with hysteresis (Newell 1965; Treiterer and Myers 1974; Zhang 1999), see Fig. 6b. From a different perspective, Kerner (2009) argues that observations show too much scatter to derive a unique fundamental relation from Kerner and Rehborn (1996), Kerner (2004). He proposes to use a three-phase approach characterized by the existence of three phases, one of them featuring a wide scatter in the density–flow plane, see Fig. 6c. As a result, the maximum flow (capacity) of a road may vary over time. An other approach to varying capacities is described by Chanut and Buisson (2003). They propose a three-dimensional fundamental relation, see Fig. 6d. This fundamental relation takes into account heterogeneity among vehicles and drivers. Therefore, the flow (in vehicles per time unit) is a function of both the density of cars and the density of trucks. The figure shows that if truck densities are relatively high, capacity is low.

2.3 Properties and requirements

Figure 7 illustrates some properties and requirements of fundamental relations. del Castillo (2012) proposes the following properties of a sound fundamental relation:

  1. 1.

    Velocity ranges from zero to a maximum value \(v_{{\rm max}}\).

  2. 2.

    Density ranges from zero to a maximum value \(\rho _{{\rm jam}}\).

  3. 3.

    Velocities at the extreme density values are \(v(0) = v_{{\rm max}}\) and \(v(\rho _{{\rm jam}}) = 0\).

  4. 4.

    Flows at the extreme density values are \(q(0) = q(\rho _{{\rm jam}}) = 0\).

  5. 5.

    Maximum velocity and congestion wave speed are the slopes of the fundamental relation at the extreme density values: \(v_{{\rm max}}= {\rm d}q / {\rm d}\rho \, (0)\) and \(w = {\rm d}q / {\rm d}\rho \, (\rho _{{\rm jam}})\).

  6. 6.

    The fundamental relation is strictly concave: \({\rm d}^2 q / {\rm d}\rho ^2 < 0\) for almost all \(\rho \in [0, \rho _{{\rm jam}}]\).

del Castillo (2012) argues that the sixth property is necessary to define a traffic flow model with a unique solution. However, there are no reasons to assume that real traffic cannot behave in a way that would be described by a fundamental relation that is not strictly concave. In fact, such fundamental relations have been proposed and used, with a unique solution (Zhang 2001). Furthermore, it is reasonable to assume that velocity does not increase with increasing density (\({\rm d}v / {\rm d}\rho \le 0\)). del Castillo does not require that directly. However, it is a necessary, but not sufficient condition for his last property on the strict concavity of the fundamental relation.Footnote 1

Fig. 7
figure 7

A sound fundamental relation and its properties, according to del Castillo (2012)

Full size image

An other important property of fundamental relations is the existence of a maximum flow, or capacity: \(q_{{\rm cap}}= \max _{0<\rho <\rho _{{\rm jam}}} q(\rho )\). Assuming that the above requirements are satisfied, the capacity is related to a single density called critical density \(\rho _{{\rm crit}}\) and a single velocity called critical velocity \(v_{{\rm crit}}\), with \(q_{{\rm cap}}= \rho _{{\rm crit}}v_{{\rm crit}}\). The critical density separates the fundamental relation into two parts: (1) a free flow branch with densities below critical, velocities above critical and increasing flow for increasing density and (2) a congestion branch with densities above critical, velocities below critical and a decreasing flow for increasing density.

In Sect. 2.1, four fundamental relations with different shapes were introduced. The Greenshields fundamental relation is the only one of them that satisfies all of del Castillo’s criteria. The other ones (the Daganzo, Smulders and Drake fundamental relation) are not strictly concave, though the first two are weakly concave and they all have non-increasing velocity (\({\rm d}v / {\rm d}\rho \le 0\)). Furthermore, in the Drake fundamental relation there is no jam density for which velocity and flow are zero.

In Sect. 2.2, fundamental relations explaining scatter were introduced. None of them satisfies del Castillo’s strict concavity requirement. Furthermore, fundamental relations with capacity drop or hysteresis imply a non-unique fundamental relation: at a certain density [usually just above (outflow) capacity] the flow is not uniquely determined by the density, but also depends on previous traffic states. The three-dimensional fundamental relation by Chanut and Buisson (2003) is not strictly concave, but it can be shown to be weakly concave in both \(\rho _{{\rm car}}\) and \(\rho _{{\rm truck}}\) and to have non-increasing velocities.

Fundamental relations, whether equilibrium or non-equilibrium, unique or non-unique, are crucial in all families of traffic flow models. In any model it is assumed that traffic is in a state on the fundamental relation, or that it tends towards it. Meso- and macroscopic models mostly include fundamental relations explicitly. Microscopic models usually have some underlying assumptions on a fundamental relation which can be revealed by careful analysis of the model or by simulation. The other components of micro- meso- and macroscopic traffic flow models will be discussed in the next sections.

3 Microscopic models

Microscopic models are the earliest family in the model tree incorporating dynamics. They are based on the assumption that drivers adjust their behavior to that of the leading vehicle. Microscopic modeling has shown to be a fruitful line of thought, which is illustrated by the large part of the model tree taken up by this family. Microscopic models describe the longitudinal (car-following) and lateral (lane-changing) behavior of individual vehicles. Only longitudinal behavior is discussed here, because adding models for lateral behavior would make the model tree much more complicated, without adding much to our aim of identifying historical trends in traffic flow modeling for the development of a new multi-class model. The microscopic model family and its most important relations is shown in Fig. 8.

Fig. 8
figure 8figure 8

Details of the genealogical tree of traffic flow models showing the microscopic model family and its most important relations

Full size image

In microscopic models, vehicles are numbered to indicate their order: \(n\) is the vehicle under consideration, \(n-1\) its leader, \(n+1\) its follower, etc., see Fig. 9. The behavior of each individual vehicle is modeled in terms of the position of the front of the vehicle \(x\), velocity \(v = {\rm d}x / {\rm d}t\), acceleration \(a = {\rm d}v / {\rm d}t = {\rm d}^2 x / {\rm d}t^2\), or a combination of the three.

Most microscopic models are car-following models. Three branches of car-following models will be discussed in Sects. 3.1 (safe-distance models), 3.2 (stimulus–response models) and 3.4 (action point models). Section 3.5 discusses extensions of car-following models. Section 3.6 discusses the most recent branch of microscopic models, namely cellular automata.

Fig. 9
figure 9

Vehicle numbering in microscopic traffic flow models (and macroscopic models in Lagrangian formulation)

Full size image

3.1 Safe-distance models

The earliest car-following models include a car-following rule based on safe following distance. Pipes (1953) proposes to express the position of the leader as a function of the position of its follower:

$$\begin{aligned} x_{n-1} = x_n + d+ Tv_n + l^{{\rm veh}}_{n-1} \end{aligned}$$
(1)

with \(d\) the distance between two vehicles at standstill and \(l^{{\rm veh}}_{n-1}\) length of the leading vehicle, see Fig. 10. \(Tv_n\) is interpreted by Pipes as the ‘legal distance’ between vehicle \(n-1\) and \(n\).

Fig. 10
figure 10

Parameters of Pipes’ safe-distance model

Full size image

Kometani and Sasaki (1961) derive a car-following model from basic Newtonian equations of motion. It is assumed that a driver acts such that he can avoid a collision even if the leader would act ‘unpredictable’. Effectively, they replace the distance at standstill \(d\) in Pipes’s model with a velocity-dependent term. Furthermore, their formulation includes a time delay \(\tau\). A positive \(\tau\) represents that it takes some time between a change in the behavior of a vehicle and the actual reaction of its follower to this change.

Gipps (1981) refines safe-distance car-following models by assuming that ‘the driver travels as fast as safety and the limitations of the vehicle permit’:

$$\begin{aligned} v_n(t+\tau )&=\min \Bigg \{ \, v_n(t) + 2.5 a_{{\rm max}}\tau \left( 1 - \frac{v_n(t)}{v_{{\rm max}}} \right) \sqrt{ 0.25 - \frac{v_n(t)}{v_{{\rm max}}} } , \qquad \qquad \quad \nonumber \\&\qquad a_{{\rm min}}\tau + \sqrt{a_{{\rm min}}^2 \tau ^2- a_{{\rm min}}\left( 2 \big ( x_{n-1}(t) - x_n(t) - s_{{\rm jam}}\big )- v_n(t) \tau - \textstyle {\frac{ v_{n-1}(t)^2 }{ b }}\right) } \, \Bigg \} \end{aligned}$$
(2)

with \(a_{{\rm max}}\) maximum acceleration, \(a_{{\rm min}}\) maximum deceleration (minimum acceleration), \(v_{{\rm max}}\) the desired (maximum) velocity and \(s_{{\rm jam}}\) jam spacing. Jam spacing is the front-to-front distance between two vehicles at standstill. Effectively, Gipps’ approach introduces two regimes: one in which the vehicle itself limits its velocity [the top part in Eq. (2)], and one in which the safe distance to the leader limits velocity (the bottom part in the equation).

The model tree shows one more development in safe-distance models. In the early years of car-following models, Newell (1961) proposed a simple safe-distance model with delay:

$$\begin{aligned} v_n = v_n \big ( x_{n-1}(t-\tau )-x_{n}(t-\tau ) \big ) \end{aligned}$$
(3)

with the function \(v_n\) at the right-hand side a fundamental relation, and \(\tau\) the delay time. Later, he simplified the model further (Newell 2002):

$$\begin{aligned} x_n(t+\tau _n) = x_{n-1}(t) - s_{{{\rm jam}},n} \end{aligned}$$
(4)

It is assumed that a vehicle follows the trajectory of its leader, translated by \(\tau _n\) and \(s_{{{\rm jam}},n}\). Leclercq et al. (2007) show that the model (4) is equivalent to a discretized macroscopic model if the Daganzo fundamental relation is applied in the macroscopic model. To show this equivalence, the macroscopic LWR model is formulated in the Lagrangian (moving) coordinate system. The formulation is also applied to develop a hybrid model that couples the microscopic Newell car-following model with the macroscopic LWR model (Leclercq 2007a). However, already Bourrel and Lesort (2003) proposed an other hybrid model combining Newell ’s earlier safe-distance model (3) with the LWR model. Finally, Laval and Leclercq (2010) propose a car-following model similar to (4) and extend it to include differences between ‘timid’ and ‘aggressive’ drivers.

3.2 Stimulus–response models

The second branch of car-following models consists of stimulus–response models. It is assumed that drivers accelerate (or decelerate) as a reaction to three stimuli:

  1. 1.

    Own current velocity \(v_n = \frac{{\rm d}{x_n}}{{\rm d}{t}}\).

  2. 2.

    Spacing with respect to leader \(s_n = x_{n-1} - x_n\).

  3. 3.

    Relative velocity with respect to leader (receding rate) \(\dot{s}_n = \frac{{\rm d}{s_n}}{{\rm d}{t}} = v_{n-1} - v_n\).

It can be seen from the model tree that in the late 1950s and early 1960s there was a rapid development of these models (Chandler et al. 1958; Herman et al. 1959; Helly 1961). The efforts consolidated in the now famous GHR-model, named after Gazis et al. (1961):

$$\begin{aligned} a_n(t) = \gamma \frac{ \big ( v_{n-1}(t) \big )^{c_1} }{ \big (s_n(t-\tau ) \big )^{c_2}} \dot{s}_n(t-\tau ) \end{aligned}$$
(5)

\(\gamma \frac{ ( v_{n-1}(t) )^{c_1} }{ ( s_n(t-\tau ) )^{c_2} }\) is considered as the sensitivity of vehicle/driver \(n\). \(\gamma\) is the sensitivity parameter and \(c_1\) and \(c_2\) are parameters that are used to fit the model to data. The receding rate \(\dot{s}_n(t-\tau )\) is considered as the stimulus, the acceleration \(a_n(t)\) as the response, hence the name ‘stimulus–response’ model.

Since those early developments, a lot of work has been done in calibrating and validating these and other similar models. However, Brackstone and McDonald (1999) concluded that stimulus–response models are being used less frequently, mainly because of contradictory findings on parameter values. Nevertheless, the model tree shows that since the mid-1990s many new models have been developed and it seems that stimulus–response models have become popular again. Some of the most popular more recent stimulus–response models are discussed below.

3.3 More recent stimulus–response models

Bando et al. (1995) introduce the optimal velocity model assuming that drivers accelerate (or decelerate) to their optimal velocity, which is a function of the headway:

$$\begin{aligned} a_n(t)&= \gamma \left( v^* \big ( s_n(t) \big ) - v_n(t) \right) \end{aligned}$$
(6)
$$\begin{aligned} v^*(s)&= v_{{\rm max}}\big ( \tanh (s-c_1) + c_2 \big ) \end{aligned}$$
(7)

with \(\gamma\) the sensitivity parameter and \(c_1\) and \(c_2\) parameters of the optimal velocity function \(v^*(s)\). Bando et al. (1998) extend their model by introducing delay \(\tau\): on the right-hand side of (6) \(t\) is replaced by \(t-\tau\).

In the intelligent driver model by Treiber et al. (2000), the acceleration is described by:

$$\begin{aligned} a = a_{{{\rm max}}} \left( 1 - \left( \frac{v}{v_{{{\rm max}}}} \right) ^\delta - \left( \frac{s^*(v, \dot{s})}{s} \right) ^2 \right) \end{aligned}$$
(8)

with \(a_{{\rm max}}\) the maximum acceleration, \(v_{{\rm max}}\) the maximum velocity and \(\delta\) the acceleration exponent. Similar to Gipps’ model, the IDM includes two regimes in the desired space gap function (Treiber and Kesting 2010):

$$\begin{aligned} s^*(v, \dot{s}) = s_{{{\rm jam}}} + \max \left( 0, Tv + \frac{ v \dot{s} }{ 2 \sqrt{a_{{{\rm max}}} a_{{{\rm min}}} } } \right) \end{aligned}$$
(9)

with \(a_{{\rm min}}\) the maximum deceleration (minimum acceleration), \(s_{{\rm jam}}\) the jam spacing and \(T\) the minimum time headway.

The latest offshoots in the branch of stimulus–response models are based on three-phase theory. The acceleration delay model by Kerner and Klenov (2006) and a stochastic car-following model by the Kerner and Klenov (2002) take into account the three traffic regimes proposed in three-phase traffic theory (Kerner and Rehborn 1996; Kerner 2009).

3.3.1 Generic stimulus–response model

Already in the earliest days of stimulus–response models Chandler et al. (1958) introduced a generic formulation:

$$\begin{aligned} a(t) = f\big ( v(t) , s(t-\tau ) , \dot{s}(t-\tau ) \big ) \end{aligned}$$
(10)

It is interesting to note that, after reformulation, most safe-distance models also fit in this framework. Therefore, the distinction between safe-distance and car-following models is not as clear as suggested by e.g., Brackstone and McDonald (1999), Hoogendoorn and Bovy (2001b). From our perspective, safe-distance models can be classified as car-following models in which the assumption that drivers keep a safe distance plays a large role. Therefore, the distinction rather lies in the assumptions than in the model equations themselves.

Currently, Wilson (2008), Wilson and Ward (2011) use the generic formulation (10) to qualitatively asses stimulus–response models. They perform stability analyses and put forward constraints on the function \(f\) and its parameters. Assuming no time delay (\(\tau =0\)), the requirements are:

  • An equilibrium fundamental relation can be derived using the steady-state solution of \(f\): \(\forall \, s > 0, \; \exists \, v = V(s) > 0\) such that \(f (v,s,0) = 0\).

  • Driving behavior is ‘rational’, leading to some constraints on the derivatives:

    • If the velocity increases, the vehicle accelerates less (or decelerates more): \({\rm d}f / {\rm d}v < 0\).

    • If the headway increases, the vehicle accelerates more (or decelerates less): \({\rm d}f / {\rm d}s \ge 0\).

    • If the relative velocity increases, the vehicle accelerates more (or decelerates less): \({\rm d}f / {\rm d}\dot{s} \ge 0\).

3.4 Action point models

The third, and last, branch of car-following models consists of action point models, first introduced by Wiedemann (1974), Brackstone and McDonald (1999). However, a decade earlier, Michaels (1965) discussed the underlying concept that drivers would only react if they perceive that they approach a vehicle. Therefore, the approach rate or the headway must reach some perception threshold before a driver reacts. The main advantage of action point models is that they incorporate, in contrast to other car-following models, that: (1) at large headways driving behavior is not influenced by that of other vehicles; and (2) at small headways driving behavior is only influenced by that of other vehicles, if changes in relative velocity and headway are large enough to be perceived.

If driving behavior is influenced by that of others, any of the previously introduced safe-distance or stimulus–response models can be used to describe the influence quantitatively.

3.5 Multi-class and multi-anticipation car-following models

Most car-following models described and analyzed in the literature assume homogeneous vehicle–driver units, that is: vehicles and drivers all behave identically. However, since each vehicle is modeled and simulated individually, it is relatively straightforward to take into account the heterogeneity. In that case, model parameters such as desired (maximum) velocity, sensitivity and reaction time may vary over vehicles and drivers. In fact, most simulation tools based on car-following models are multi-class, i.e., they do take into account heterogeneity.

Multi-anticipation is another way to extend car-following models. In this case, more than one leading vehicle influences the behavior of a driver. The concept was already used in the car-following model by Helly (1961) and Brackstone and McDonald (1999). However, it has become widespread since Bexelius (1968) developed a multi-anticipation version of the GHR model. More recently, multi-anticipation was incorporated in the optimal velocity model (Lenz et al. 1999) and the intelligent driver model (Treiber et al. 2006a). Finally, multi-anticipation and multi-class have been combined to take into account that some drivers look further ahead than others (Ossen and Hoogendoorn 2006).

3.6 Cellular-automata models

Cellular-automata models are usually categorized as microscopic models, even though they are a different, and much younger, branch in the model tree. This is because the movement of individual vehicles is modeled. The main difference with car-following models is that space is discretized. The road is partitioned into cells of usually 7.5 m long. In a cell either a vehicle might be present or not. The model consists of a set of rules that determine when the vehicle will move to the next (downstream) cell. The first cellular-automata traffic flow models was introduced by Cremer and Ludwig (1986). The model by Nagel and Schreckenberg (1992) is regarded as the prototype cellular-automata model (Knospe et al. 2004).

More recent developments combine cellular-automata models with the optimal velocity car-following model Helbing and Schreckenberg (1999) or three-phase theory Kerner et al. (2002). Some of the most popular cellular-automata models are compared by Knospe et al. (2004).

4 Mesoscopic models

Mesoscopic traffic flow models were developed to fill the gap between the family of microscopic models that describe the behavior of individual vehicles, and the family of macroscopic models that describe traffic as a continuum flow. Mesoscopic models describe vehicle behavior in aggregate terms such as in probability distributions. However, behavioral rules are defined for individual vehicles. The family includes headway distribution models (Buckley 1968; Branston 1976) and cluster models (Mahnke and Kühne 2007). We discuss the most popular branches, namely, gas-kinetic models (Sect. 4.1) and macroscopic models derived from them (Sect. 4.2). The mesoscopic model family and its most important relations is shown in Fig. 11.

Fig. 11
figure 11

Details of the genealogical tree of traffic flow models showing the mesoscopic model family and its most important relations

Full size image

4.1 Gas-kinetic models

Gas-kinetic models were developed in analogy to models describing the motion of large numbers of small particles (atoms or molecules) in a gas. When applied to traffic flow, these models describe the dynamics of velocity distribution functions of vehicles. Prigogine and Andrews (1960), Prigogine (1961) first introduce gas-kinetic models describing traffic flow by the following partial differential equation:

$$\begin{aligned} \frac{\partial {\tilde{\rho }}}{\partial {t}} + v \frac{\partial {\tilde{\rho }}}{\partial {x}} = \left( \frac{\partial {\tilde{\rho }}}{\partial {t}} \right) _{{\rm acceleration}} + \left( \frac{\partial {\tilde{\rho }}}{\partial {t}} \right) _{{\rm interaction}} \end{aligned}$$
(11)

with \(\tilde{\rho }\) the reduced phase-space density, which can be interpreted as follows. At time \(t\), the expected number of vehicles between location \(x\) and \(x + {\rm d}x\) that drive with a velocity between \(v\) and \(v + {\rm d}v\) is the integral of the reduced phase-space density over this two-dimensional area:

$$\begin{aligned}&\hbox {expected} \# \hbox {of veh's in} [x,x+{\rm d}x) \hbox {with velocity in} [v,v+{\rm d}v)\nonumber \\&\quad = \int \limits _x^{x+{\rm d}x} \int \limits _v^{v+{\rm d}v} \tilde{\rho }(x,v,t) \, {\rm d}x \, {\rm d}v \; \approx \; \tilde{\rho }(x,v,t) \, {\rm d}x \, {\rm d}v \end{aligned}$$
(12)

where the approximation holds in the limit for an infinitesimal area with \({\rm d}x \rightarrow 0\) and \({\rm d}v \rightarrow 0\). The left-hand side of (11) consists of a time derivative and an advection term describing the propagation of the phase-space density with the vehicle velocity. At the right-hand side, there is an acceleration term describing the acceleration towards the equilibrium velocity. The other term at the right-hand side is an interaction term, or collision term, describing the interaction between nearby vehicles.

Paveri-Fontana (1975) improves this gas-kinetic model by relaxing the assumption that the behavior of nearby vehicles is uncorrelated, which results in an adapted interaction term. In the mid-1990s, a revival of gas-kinetic models occurred with the development of a multi-lane version of Paveri-Fontana’s model, Helbing (1997). Hoogendoorn and Bovy (2001a) propose a generic gas-kinetic traffic flow model including the previously mentioned models (Prigogine and Andrews 1960; Paveri-Fontana 1975; Helbing 1997) as special cases.

4.2 Continuum gas-kinetic models

Gas-kinetic models are usually not applied in simulations as such, but a continuum traffic flow model is derived and simulations are based on this continuum model. Examples are the models by Phillips (1979), Treiber et al. (1999) and Helbing et al. (2001). Hoogendoorn (1999) derives a multi-class multi-lane continuum traffic flow model from a gas-kinetic model. Finally, Tampère et al. (2003) propose a continuum gas-kinetic model that explicitly includes a simple car-following model.

5 Macroscopic models

Macroscopic traffic flow models form the fourth, and last, family in the model tree. They describe traffic flow as if it were a continuum flow and are often compared to, or derived in analogy with, continuum models for fluids. Individual vehicles are not modeled, however aggregated variables such as (average) density and (average) flow are used. In this section, we discuss the major branches of macroscopic models, namely, kinematic wave models (Sect. 5.1), their multi-class extensions (Sect. 5.2) and higher-order models (Sect. 5.3). The macroscopic model family and its most important relations is shown in Fig. 12.

5.1 Kinematic wave models

Macrosopic traffic flow models were first introduced by Lighthill and Whitham (1955b) and, independently, Richards (1956). Their model is the prototype kinematic wave model, and was named the LWR model later. The dynamics of traffic is described by a partial differential equation, which models the conservation of vehicles:

$$\begin{aligned} \frac{\partial {\rho }}{\partial {t}} + \frac{\partial {}}{\partial {x}} \big ( q(\rho ) \big ) = 0 \end{aligned}$$
(13)

and a fundamental relation \(q = q(\rho )\).

Because of its simplicity, the LWR model has received both much attention and critique. The model tree shows that this resulted in many offshoots. The main drawback is that vehicles are assumed to attain the new equilibrium velocity immediately after a change in the traffic state, which implies infinite acceleration. This problem is addressed by higher-order models (see Sect. 5.3), and also by variants of the LWR model. For example, Lebacque (2002), Leclercq (2007b) introduce bounded-acceleration. An other drawback of the LWR model is that breakdown (the transition from the free flow regime to the congestion regime) always occurs at the same density and without capacity drop or hysteresis. This is addressed by Daganzo et al. (1997), Laval and Daganzo (2006) and Jin (2010) by introducing lane changing in a discretized version of the LWR model (Daganzo 1994; Lebacque 1996). The stochastic kinematic wave model proposed by Hoogendoorn et al. (2009) uses breakdown probabilities to reflect that breakdown might occur at different densities. Scattered fundamental diagrams are also reproduced by other stochastic kinematic wave models such as the one introduced in Jabari and Liu (2012, 2013).

Fig. 12
figure 12figure 12

Details of the genealogical tree of traffic flow models showing the macroscopic model family and its most important relations

Full size image

5.2 Multi-class kinematic wave models

In the last decade, the branch of multi-class kinematic wave models has developed quickly. This follows the earlier development of other types of multi-class models (micro- and mesoscopic, higher-order macroscopic).

Daganzo (2002) proposes a multi-class multi-lane model based on the LWR model. It is assumed that there are two types of drivers: ‘slugs’ who drive slow and have little incentive to overtake, and ‘rabbits’ who attempt to drive fast and overtake more often. Other multi-class kinematic wave models are single-pipe. This implies that there might be multiple lanes, however they are not distinguished in the model and overtakings or differences between the lanes are not taken into account explicitly.

The model tree shows that Wong and Wong (2002) were the first to introduce such a single-pipe multi-class kinematic wave model. They propose to use a class-specific version of the conservation equation for each of the \(U\) classes (13):

$$\begin{aligned} \frac{\partial {\rho _u}}{\partial {t}} + \frac{\partial {q_u}}{\partial {x}} = 0 \end{aligned}$$
(14)

with \(\rho _u\) the class-specific density of class \(u\), \(q_u=\rho _u v_u\) the class-specific flow, and \(v_u\) the class-specific velocity. The class-specific velocity depends on the total vehicle density. Effectively, the vertical axes of the density–velocity fundamental relations are scaled differently for each class, see Fig. 13a, b. It has been found that multi-class models are able to reproduce phenomena related to scatter in the fundamental diagram better than mixed-class models (Treiber and Helbing 1999; Daganzo 2002; Wong and Wong 2002; Ngoduy 2011; Bellomo and Dogbe 2011) and references therein.

Fig. 13
figure 13

Different shapes of two-class fundamental relations in. Solid lines indicate car velocity and broken lines truck velocity (two-class fundamental relations.)

Full size image

Benzoni-Gavage and Colombo (2003), Chanut and Buisson (2003) include the difference in length between the classes in the fundamental relation. Effectively, they scale both axes of the fundamental relation differently for each class. Chanut and Buisson show that, in the case of two classes, this leads to a three-dimensional fundamental relation, see Fig. 6d.

Ngoduy and Liu (2007) use a similar approach for the fundamental relation with state-dependent parameters. The parameters include the passenger car equivalent (pce) value, which expresses how much a vehicle adds to the flow relatively to a passenger car. For example, a light truck may count as 1.5 passenger cars, whereas a heavy truck may count as three passenger cars. This model was later extended to include a discontinuous fundamental relation (Ngoduy 2010) and a stochastic term was included (Ngoduy 2011).

The two-class model by Logghe and Immers (2008) includes a three-state fundamental relation, see Fig. 13c. It consists of a free flow, a congestion and a semi-congestion state. In semi-congestion one class (cars) behaves as if it is in a congested regime (for increasing density, car flow decreases), while the other class (trucks) behaves as if it is in free flow (for increasing density, truck flow increases).

Fastlane is a recent offshoot in the branch of multi-class kinematic wave models (van Lint et al. 2008; van Wageningen-Kessels et al. 2014). It takes a different approach without rescaling the fundamental relation. Instead, an effective density is computed and this is used as input for the fundamental relation. The fundamental relation now expresses the class specific velocity as a function of the effective density, see Fig. 13d. The effective density is a weighted summation of the class-specific densities:

$$\begin{aligned} \rho = \sum _u \eta _u(\rho ) \rho _u \end{aligned}$$
(15)

with \(\eta _u\) the pce value:

$$\begin{aligned} \eta _u(\rho ) = \frac{\omega _u}{\omega _1} = \frac{ L_u + T_u v_u(\rho ) }{ L_1 + T_1 v_1(\rho ) } \end{aligned}$$
(16)

with \(\omega _u\) the ‘space occupancy’ of one vehicle of class \(u\). The space occupancy is based on Pipes’ safe-distance car following model with \(L_u = l + d= s_{{{\rm jam}},u}\) the vehicle spacing at standstill if there would only be vehicles of class \(u\). \(T_u\) denotes the minimum time headway of vehicles of class \(u\).

The most recent multi-class kinematic wave model is the porous flow model by Nair et al. (2012). It considers heterogeneous traffic on a two-dimensional roadway. Small vehicles can drive through ‘pores’: openings between other vehicles. It is developed to model disordered traffic flow with different types of vehicles such as cars, scooters and bikes and without lanes.

Finally (in van Wageningen-Kessels et al. 2013, 2014), we show that a slight generalization of Fastlane leads to a generic single-pipe multi-class kinematic wave model, including all such models known from the literature and introduced before.

5.3 Higher-order models

Higher-order models form the last branch of macroscopic traffic flow models. They include an equation describing the acceleration (‘velocity dynamics’) towards the equilibrium velocity described by a fundamental relation. Payne (1971) derived a macroscopic traffic flow model from a simple stimulus–response car-following model. It yielded a model consisting of the fundamental relation and two-coupled partial differential equations, hence the name higher-order model. The partial differential equations are the conservation of vehicles Eq. (13) and an equation describing the velocity dynamics:

$$\begin{aligned} \frac{\partial {v}}{\partial {t}} + v \frac{\partial {v}}{\partial {x}} = \frac{v^*(\rho ) - v}{t_{{\rm relax}}} - \frac{c^2}{\rho } \frac{\partial {\rho }}{\partial {x}} \end{aligned}$$
(17)

with \(v^*(\rho )\) the equilibrium velocity described by the fundamental relation. The parameters in the model are interpreted differently by different authors. For example, Zhang (2001) interprets \(t_{{\rm relax}}\) as the relaxation time and \(c^2=\mu / t_{{\rm relax}}\) is the ‘sound speed’ with \(\mu\) the anticipation coefficient.

Daganzo (1995) has argued that higher-order models are flawed because they are not anisotropic, implying that in these models vehicles may drive backward. In general, anisotropy means that characteristic waves are not faster than vehicles. In the time Daganzo’s article was written, existing higher-order models were indeed not anisotropic. The publication has lead to rapid developments of new higher order models that resolve the problems. Probably the most well known of them is the model by Aw and Rascle (2000). They propose, instead of Payne’s velocity Eq. (17), the following one:

$$\begin{aligned} \frac{\partial {}}{\partial {t}} \left( v+p(\rho ) \right) + v \frac{\partial {}}{\partial {x}} \left( v+p(\rho ) \right) = 0 \end{aligned}$$
(18)

with \(p(\rho )\) a ‘pressure term’. The (increasing) function \(p(\rho )\) can have different forms, but \(p(\rho )=\rho ^c\) with some constant \(c>0\) is considered as the prototype. In this model, when parameters have been chosen correctly, characteristic waves cannot be faster than vehicles. This is also the case in the model by Zhang (1999), which is an adaptation of Payne’s model which includes hysteresis. A multi-class version of Aw and Rascle’s model has been proposed later (Bagnerini and Rascle 2003). Furthermore, Lebacque et al. (2007) develop a generalized higher-order model that includes the models by Aw and Rascle (2000), Zhang (1999) as special cases.

Finally, Aw et al. (2002), Moutari and Rascle (2007) develop a hybrid model that couples the model by Aw and Rascle with a microscopic version of it. Similarly to Leclercq (2007a) (see Sect. 3.1) they simplify the coupling by applying the Lagrangian formulation of the macroscopic model. There has been more recent work on Lagrangian reformulations of both kinematic wave and higher order models (Aw et al. 2002; Leclercq et al. 2007; van Wageningen-Kessels et al. 2010), but they are not included in the model tree because they are only reformulations of existing models and not new models.

6 Discussion and conclusions

In the previous sections, many traffic flow models and their position in the model tree have been discussed. In the model tree, several trends can be identified:

  • Certain branches converge towards a generalized model. The generalized model can be used to analyze qualitative properties of all models within that branch (Wilson 2008; Hoogendoorn and Bovy 2001a; del Castillo 2012; van Wageningen-Kessels et al. 2013, 2014).

  • The LWR model is extended and adapted to better reproduce key phenomena such as capacity drop, hysteresis and scattered fundamental diagrams (Zhang 1999; Lebacque 2002; Wong and Wong 2002).

  • Multi-class versions of previously developed models are introduced (Hoogendoorn 1999; Bagnerini and Rascle 2003; Ossen and Hoogendoorn 2006), and especially multi-class kinematic wave models (Wong and Wong 2002; Benzoni-Gavage and Colombo 2003; Chanut and Buisson 2003; Zhang et al. 2006; Laval and Daganzo 2006; Ngoduy and Liu 2007; Logghe and Immers 2008; van Lint et al. 2008; van Wageningen-Kessels et al. 2014; Nair et al. 2012).

  • Hybrid models combine microscopic and macroscopic models (Bourrel and Lesort 2003; Leclercq 2007a; Moutari and Rascle 2007).

From the available literature we also observe that there is a tension between, on the one hand, highly detailed models which are complex and supposed to describe reality very accurately and, on the other hand, simple and traceable models that are applicable in real-time applications such as proactive traffic management. We now look into this in more detail, and will conclude with our own choices in traffic flow models and suggestions for future research.

6.1 Macroscopic modeling and the continuum assumption

The first macroscopic traffic flow model was derived in analogy with a model for river flow (Lighthill and Whitham 1955a, b). It has been argued that the differences between fluid flow (including that of gasses) and traffic flow are too large to justify a continuum approach. For example, Darbha et al. (2008), Tyagi et al. (2008), and Bellomo and Dogbe (2011) argue that there are very few vehicles in the area of interest (at most a few 100/km), unlike in for example many applications in thermodynamics with around \(10^{23}\) particles/cm\(^3\). However, Papageorgiou (1998) uses the limited number of vehicles only as an argument that the descriptive accuracy of macroscopic traffic flow models will never reach the same level as in other domains such as Newtonian physics or thermodynamics. Furthermore, he argues that the descriptive accuracy of macroscopic models remains low when compared to models in other domains because vehicles and drivers all behave differently, and change their behavior over time, unlike molecules which follow (usually simple and constant) physical laws. Additionally, we argue that because drivers all have similar goals (same direction, similar desired velocity) and usually prefer not to accelerate or decelerate often, their behavior may be more alike than that of particles in a fluid. This implies that the continuum assumption is reasonable for traffic flow, if one does not seek too much descriptive detail.

6.2 Microscopic models and parameters

Traffic flow models are often criticized for having many parameters, whose values are difficult to estimate because of the dynamics of the system (Orosz et al. 2010). This especially holds for microscopic models (Brackstone and McDonald 1999; Bellomo and Dogbe 2011). An extreme example is the deterministic acceleration time delay three-phase traffic flow model based on three-phase theory with 19 parameters (Kerner 2009). Microscopic models which include heterogeneity or stochasticity may include even more parameters. Moreover, traffic flow models often include parameters that are not easily observable or even have no physical interpretation at all. For example, the constants \(c_1\) and \(c_2\) in the GHR model and the acceleration exponent \(\delta\) in the IDM have no physical interpretation and are only used to fit the simulation results to data. Other parameters such as maximum and minimum acceleration \(a_{{\rm max}}\) and \(a_{{\rm min}}\) do have a physical interpretation, but are not easily observable. To observe those parameters, one would need detailed trajectory data including observations where this maximum (or minimum) acceleration is realized. Similar arguments hold for models including a fundamental diagram. The critical and jam density can only be observed if the data includes moments where traffic is in such as state. Furthermore, traffic flow models are sometimes criticized for having unrealistic parameter values. For example, Brackstone and McDonald (1999) concluded that contradictory findings on parameter values \(c_1\) and \(c_2\) in the GHR model are the main reason why it is being used less frequently. In general, macroscopic models have less parameters which are more easily observable than microscopic models.

6.3 Model applications

Finally, one has to consider the application of traffic flow models. Therefore, descriptive and predictive accuracy have to be weighted against the need for fast simulations. For example, proactive traffic management uses models to estimate, predict and control traffic states. Therefore, models need to allow for fast simulations. If optimal control is applied, it is furthermore desirable that the model has a simple mathematical formulation. A continuum model with a simple fundamental relation would be the most obvious choice. Moreover, though new computers will be faster than current ones, the need for fast simulations will remain, e.g., for the comparison of many scenario’s on large networks.

An other example of a model application is long-term planning and design of roads. In such cases, fast simulations are of minor importance and it is much more important that models give accurate predictions on future traffic states, allow the evaluation of different scenarios, and may even take into account stochasticity. A more accurate model, possibly a stochastic car-following model or a model with a stochastic fundamental diagram would be a more obvious choice in these applications.

Wilson (2008) has argued that ‘we can expect over the next few years to definitively resolve the conflict between the various traffic modeling schools’, using novel, more detailed data. However, in each application the weights of the various criteria may be different. That is why the model tree shows divergence and many different branches have developed. Furthermore, this has lead to the development of hybrid models. Even within one application it may be necessary to have detailed simulation results in certain regions (e.g., the main roads of an urban area that needs to be controlled) and a less detailed, but fast, result is sufficient in the rest of the network (e.g., the roads surrounding the urban area that are not controlled).

6.4 Future research

The model tree can help in identifying future research and model development directions. For example, most branches include multi-class models. However, the development of multi-class models seems to lag behind for the branch of cellular-automata models and for hybrid models. Future research is not limited to extending each of the families and their branches further. More valuable results may be obtained by combining ideas from different branches. For example, hybrid models have been proposed but can be developed much further. They are able to combine the advantages of different types of models. It would be interesting to combine, for example, mesoscopic models with microscopic or macroscopic models. Furthermore, a new branch of hybrid models can combine mixed-class and multi-class models. Finally, current generalized models include many models, but not all. Further generalizations can be developed and used to efficiently compare existing and new models.

In our research, we combine the trends in the model tree and develop a multi-class kinematic wave traffic flow model (van Lint et al. 2008; van Wageningen-Kessels et al. 2014; van Wageningen-Kessels 2013). Furthermore, we generalize the model such that it allows for a qualitative analysis of the properties of this and similar models (van Wageningen-Kessels et al. 2013; van Wageningen-Kessels 2013). Finally, we propose a reformulation in Lagrangian coordinates which simplifies hybridization of the model (van Wageningen-Kessels et al. 2010; van Wageningen-Kessels 2013).