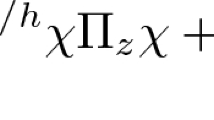1 Introduction

We discuss global estimates of resonances in terms of the potential for Schrödinger operators \(H=H_0+q\), where the unperturbed operator \(H_0\) is one of the following:

$$\begin{aligned} \begin{aligned}&Case \ 1: \qquad -{d^2/dx^2}\quad \mathrm{in}\quad L^2({\mathbb R}).\\&Case \ 2: \qquad -{d^2/dx^2}\quad \mathrm{in}\quad L^2({\mathbb R}_+),\quad \mathrm{with} \ f(0)=0 \ \mathrm{boundary\ conditions}.\\&Case \ 3: \qquad -{d^2/dx^2}\quad \mathrm{in}\quad L^2({\mathbb R}_+),\quad \mathrm{with}\ \ f'(0)=0 \ \mathrm{boundary\ conditions}. \end{aligned} \end{aligned}$$

We assume that q is real, integrable and has a compact support. It is well known that the spectrum of H consists of an absolutely continuous part \([0,\infty )\) and a finite number of simple negative eigenvalues \(E_1<\cdots<E_m<0\), see well-known papers [5, 22] and the book [20] about inverse scattering. The Schrödinger equation

$$\begin{aligned} -f''+q(x)f=k^2f,\ \ \ \ \ \ k\in {\mathbb C}{\setminus }\{0\}, \end{aligned}$$
(1)

has unique solutions \(\psi _{\pm }(x,k)\) such that \(\psi _+(x,k )=e^{ixk }\) for large positive x and \(\psi _-(x,k)=e^{-ik x}\) for large negative x. Outside the support of q any solutions of (1) have to be combinations of \(e^{\pm ik x}\). The functions \(\psi _\pm (x,\cdot ), \psi _\pm '(x,\cdot )\) for all \(x\in {\mathbb R}\) are entire. We define the Wronskian w for Case 1 by

$$\begin{aligned} \begin{aligned} w(k )=\{\psi _-(\cdot ,k), \psi _+(\cdot ,k )\},\qquad \end{aligned} \end{aligned}$$
(2)

where \(\{f, g\}=fg'-f'g\). In Case 2 the Jost function is defined as \(\psi _+(0,\cdot )\) and in Case 3 the Jost function is defined as \(\psi _+'(0,\cdot )\). Let F be one of the functions \(w, \psi _+(0,k )\) or \(\psi _+'(0,k )\). Recall that the function F is entire. One has exactly m simple zeros \(k_{1}=i|E_1|^{1/2},\ldots k_{m}=i|E_{m}|^{1/2}\) in the upper half-plane \({\mathbb C}_+\) and for \(q\ne 0\) an infinite number of zeros \((k_{n})_{m+1}^{\infty }\) in the lower half-plane \(\overline{{\mathbb C}}_-\) labeled by

$$\begin{aligned} 0\le |k_{m+1}|\le |k_{m+2}|\le \dots \qquad where \qquad 0<|k_{m+2}|, \end{aligned}$$

see [9, 24, 27] and [16]. Here it is possible that \(k_{m+1}=0\) for some potential, but \(0<|k_{m+2}|\) for any potential. By definition, a zero \(k_n\in \overline{{\mathbb C}}_-\) of F is called a resonance of H. The multiplicity of the resonance is the multiplicity of the corresponding zero of F. Of course, the energies are given by \(k^2\), but since k is the natural parameter, we will abuse the terminology.

There are only few estimates of resonances. We denote the number of zeros of function f having modulus \(\leqslant r\) by \({\mathcal N}(r,f)\), each zero being counted according to its multiplicity.

Firstly, Zworski [27] determines the asymptotics of the counting function for resonances:

$$\begin{aligned} {\mathcal N}(r,w)=\frac{2 r}{\pi }(\gamma +o(1))\qquad \mathop {\mathrm {as}}\nolimits \quad r\rightarrow \infty , \end{aligned}$$
(3)

where \([0,\gamma ]\) is the convex hull of the support of q. Note that (3) holds true for the case 2 and 3 (see [14, 24]).

Secondly, let \({\mathscr {N}}_t\) denote the number of resonances and eigenvalues in the half-plane \(\{\mathop {\mathrm {Im}}\nolimits k>t\}, t<0\). Then there is a constant \({\mathcal C}_q\) (see Theorem 3.11 in [8]) such that the following estimate holds true:

$$\begin{aligned} {\mathscr {N}}_t\leqslant {\mathcal C}_q\biggr (1+\int \int _{{\mathbb R}^2}e^{4|t||x-y|}|q(x)||q(x)|dxdy\biggr ), \end{aligned}$$
(4)

where \({\mathcal C}_q\) is some constant depending on \(\Vert q\Vert \), but not on t. Unfortunately, (4) is not sharp, since \({\mathcal C}_q\) is unknown.

Thirdly, for the Case 2 (at \(\gamma =1\)) there are simple estimates from [14]

$$\begin{aligned} |k_n|e^{-2|\mathop {\mathrm {Im}}\nolimits k_n|}\leqslant \Vert q\Vert e^{\Vert q\Vert },\qquad \qquad \mathrm{where} \ \ \Vert q\Vert =\int _{\mathbb R}|q(x)|dx, \end{aligned}$$
(5)

for any \(k_n\in {\mathbb C}_-\). Note that this estimate yields the will-known logarithmic curve for forbidden domain.

Define the constant Q by

$$\begin{aligned} Q=\max \{\Vert q\Vert ,\Vert q\Vert _1\},\qquad \Vert q\Vert =\int _{\mathbb R}|q(t)|dt,\qquad \Vert q\Vert _1=\int _{\mathbb R}|tq(t)|dt. \end{aligned}$$
(6)

We present a theorem about new estimates of counting functions.

Theorem 1.1

Let \(H=H_0+q\), where q is integrable and has compact support.

In Case 1, let \(\mathop {\mathrm {supp}}\nolimits q\subset [0, \gamma ]\) but in no smaller interval.

In Cases 2 and 3, let \(\gamma =\sup (\mathop {\mathrm {supp}}\nolimits (q))\).

Let \(r>0\) and \(r_1=r+{12}\). Then the following estimates hold true:

$$\begin{aligned}&{\mathcal N}(r,w)\leqslant {\frac{1}{\log 2}}\biggr ({\frac{4r_1\gamma }{\pi } }+\log (1+{4r_1})+ {\frac{9Q}{1+4r_1}}\biggr ),\end{aligned}$$
(7)
$$\begin{aligned}&{{\mathcal N}(r,\psi _+(0,\cdot ))+{\mathcal N}(r,\psi _+'(0,\cdot ))2}\nonumber \\&\quad \leqslant {\frac{1}{\log 2}}\biggr ({\frac{4r_1\gamma }{\pi } }+\log (1+{4r_1})+{\frac{9\Vert q\Vert \max \{1,\gamma \}}{1+4r_1}}\biggr ). \end{aligned}$$
(8)

The proof is based on the Jensen formula and standard estimates of the fundamental solutions. The RHS in (2) has asymptotics \({\frac{2}{\log 2}}{\frac{2 r}{\pi }}(\gamma +o(1))\) as \(r\rightarrow \infty \). If we compare this asymptotics with (3), then we obtain the coefficient \({\frac{2}{\log 2}}\). It means that the estimate (7) is sufficiently exact, but weaker than what asymptotics (3) gives.

We present our main result.

Theorem 1.2

Let \(H=H_0+q\), where q is integrable and has compact support.

In Case 1, let \(\mathop {\mathrm {supp}}\nolimits q\subset [0, \gamma ]\) but in no smaller interval.

In Cases 2 and 3, let \(\gamma =\sup (\mathop {\mathrm {supp}}\nolimits (q))\).

Then for any \(p>1\) the following estimates hold true:

$$\begin{aligned} \begin{aligned} \sum _{\pm \mathop {\mathrm {Im}}\nolimits k_n\leqslant 0} {\frac{1}{| k_n\mp 2i|^{p}}}\leqslant CY_p\biggr (1+{\frac{\gamma }{\pi } }+{\mathcal Q}\biggr ), \end{aligned} \end{aligned}$$
(9)

where \(C\leqslant 2^5\) is an absolute constant, \(Y_p=\sqrt{\pi }\Gamma (\frac{p-1}{2})/\Gamma (\frac{p}{2})\) and

$$\begin{aligned} {\mathcal Q}= {\left\{ \begin{array}{ll} \max \{\Vert q\Vert ,\Vert q\Vert _1\} &{} Case \ 1\\ 2\Vert q\Vert \max \{1, \gamma \}, &{} Case\ 2,3 \end{array}\right. }. \end{aligned}$$
(10)

Remark

  1. 1.

    The function \(Y_p, p>1\) is strongly monotonic and convex on \((1,\infty )\), since \(Y_p'<0, Y_p''>0\), and satisfies

    $$\begin{aligned} Y_2=\pi ,\qquad Y_p={\left\{ \begin{array}{ll} {\frac{1}{\sqrt{p}}}(\sqrt{2\pi }+O(1/p)) &{} \mathop {\mathrm {as}}\nolimits \quad p\rightarrow \infty \\ {\frac{1}{p-1}}(2+o(1)) &{} \mathop {\mathrm {as}}\nolimits \quad p\rightarrow 1\end{array}\right. }. \end{aligned}$$
    (11)

    Thus we can control the RHS of (9) at \(p\rightarrow 1\) and for large \(p\rightarrow \infty \). Note we take \(p>1\), since the asymptotics (3) implies the simple fact \(\sum _{k_n\ne 0} {1|k_n|}=\infty \), see p. 17 in [18].

  2. 2.

    The RHS of (9) depends on 3 crucial parameters: \(p>1\), the diameter of the support of the potential and the magnitude \(\Vert q\Vert \) of the potential. In Cases 1 and 3 we can not remove 1 in the RHS of (9). In Case 2 probably the number 1 should be absent in the RHS of (9). In order to explain this we need to add that at \(q=0\) there is a resonance in the Cases 1 and 3, but there is no a resonance in the Case 2.

  3. 3.

    In Case 1 the proof of (9) is based on analysis of the function w. We use harmonic analysis and the Carleson Theorem (Theorems 1.56 and 2.3.9 in [10]) about Carleson measure. The proof for Cases 2 and 3 is a simple corollary of Case 1.

  4. 4.

    C is the constant from Carleson’s Theorem ([1, 2] and see Theorems 1.56 and 2.3.9 [10]).

  5. 5.

    In fact, the estimates (7), (9) give a new global property of resonance stability.

  6. 6.

    It is well-known that the Jost function is a Fredholm determinant, see [12]. In Case 1 we consider the Fredholm determinant \(D(k)=\mathop {\mathrm {det}}\nolimits (I+q(H_0-k^2)^{-1}), k\in {\mathbb C}_+\). The function D is analytic in the upper half-plane (see e.g. [9]) and satisfies the well-known identity \(D(k)={\frac{w(k)}{2ik}}\) for all k. Thus Theorem 1.2 describes the zeros of the determinants also.

Resonances for the multidimensional case were studied by Melrose, Sjöstrand, and Zworski and other, see [23, 25, 28]) and references therein. We discuss the one dimensional case. A lot of papers are devoted to resonances for the 1D Schrödinger operator, see Froese [9], Korotyaev [17], Simon [24], Zworski [27], and references therein. Different properties of resonances were determined in [8, 24, 27], and [14, 16, 17]. Korotyaev solved the inverse problem for resonances for the Schrödinger operator with a compactly supported potential on the real line [16] and the half-line [14]: (i) the characterization of S-matrix in terms of resonances, (ii) a recovering of the potential from the resonances, (iii) the potential is uniquely determined by the resonances (about uniqueness see also [3, 29]).

The “local resonance” stability problem was considered in [15] for Case 2. Roughly speaking, if \((k_n)_1^\infty \) is a sequence of eigenvalues and resonances of the Schrödinger operator with some compactly supported potential q and \(\sum _{n\ge 1}n^{2\varepsilon }|k_n-k_{n}^\bullet |^2<\infty \) for some sequence \((k_n^\bullet )_1^\infty \) and \(\varepsilon >1\), then \((k_n^\bullet )_1^\infty \) is a sequence of eigenvalues and resonances of a Schrödinger operator for some unique real compactly supported potential \( q_\bullet \).

Finally we note that some stability results (quite different type, so-called stability for finite data) were obtained by Marlettta et al. [21].

A lot of papers are devoted to estimates of eigenvalues in terms of the potential. We recall Lieb–Thirring type inequalities ([19]) from [6] given by:

Let V be a non-negative, unbounded potential, such that the Schrödinger operator \(-\Delta +V\) in \(L^2({\mathbb R}^d)\) has an unbounded sequence of discrete eigenvalues \(\lambda _1\leqslant \lambda _2\leqslant \cdots \). Then

$$\begin{aligned} \sum _{n\ge 1} |\lambda _n|^{-{\frac{p}{2}}}\leqslant {\frac{C_p(d)}{(4p)^{\frac{d}{2}}}} \int _{{\mathbb R}^d} V(x)^{{\frac{d-p}{2}}}dx,\quad {where} \quad C_p(d)={\frac{\Gamma ({\frac{p-d}{2}})}{\Gamma ({\frac{p}{2}})}},\nonumber \\ \end{aligned}$$
(12)

for all \( p>d\). The inequality is derived from inequalities by Golden [4] and Thompson [26]. It is interesting that (9) and (12) (at \(d=1\)) have the same constant \(C_p(1)=Y_p\).

In our case (9) the number of resonances is infinite and we consider also the power \(p>1\). Furthermore, some resonances and eigenvalues can be close to zero even for small potentials. For this reason, we sum \(|k_n-2i|^{-{p}}\) and \(|k_n+2i|^{-{p}}\). Thus, roughly speaking, (9) is a Lieb–Thirring type inequality for the resonances (Loss, private communication).

We shortly describe the proof of main Theorem 1.2. We use results about the Carleson measure. Recall that a positive Borel measure M defined in \({\mathbb C}_-\) is called a Carleson measure if there is a constant \(C_M\) such that for all \((r,t)\in {\mathbb R}_+\times {\mathbb R}\)

$$\begin{aligned} M(D_-(t,r))\le C_Mr,\ \ \ \mathrm{where}\ \ \ \ D_-(t,r)\equiv \{z\in {\mathbb C}_-: |z-t|<r \}, \end{aligned}$$
(13)

here \(C_M\) is the Carleson constant independent of (t, r).

We consider that case when the Wronskian w has not zeros in the upper half-plane, the proof of other cases is similar. For an entire function w with zeroes \(k_n, n\ge 1\) we define an associated measure by

$$\begin{aligned} d\Omega (k,w)=\sum _{\mathop {\mathrm {Im}}\nolimits k_n\leqslant 0} \delta (k-k_n+i)du dv,\qquad k=u+iv\in {\mathbb C}_-, \end{aligned}$$
(14)

where \(\delta \) is the delta-function. In order to prove Theorem 1.2 show that the measure \(\Omega (k,w)\) is the Carleson measure. In the proof we obtain different type of estimates of the Wronskian w, and in particular we prove Theorem 1.1. We underline that the main problem is to get the best Carleson constant in terms of potentials.

After this we use the following Carleson result (see p. 63, Theorem 3.9, [10]):

Let F be analytic on \({\mathbb C}_-\). For \(0<p<\infty \) we say F belongs the Hardy space \( {\mathscr {H}}_p={\mathscr {H}}_p({\mathbb C}_-)\) if

$$\begin{aligned} \sup _{y<0}\int _{\mathbb R}|F(x+iy)|^pdx=\Vert F\Vert _{{\mathscr {H}}_p}^p<\infty . \end{aligned}$$

We define the Hardy space \({\mathscr {H}}_p\) for the case \({\mathbb C}_-\), since below we work with functions on \({\mathbb C}_-\).

If M is a Carleson measure and satisfies (13), then the following estimate holds:

$$\begin{aligned} \int _{{\mathbb C}_-} |F|^pdM\le C C_M \Vert F\Vert _{{\mathscr {H}}_p}^p\qquad \forall \quad F\in {\mathscr {H}}_p, \ p\in (0,\infty ), \end{aligned}$$
(15)

where \(C_M\) is the so-called Carleson constant from (13) and \(C\leqslant 2^5\) is an absolute constant.

Thus in order to prove the main theorem we apply (15) to the functions \(F(k)={\frac{1}{k-i}}\) and \(dM=d\Omega \).