Introduction

Nanofluids are a new kind of heat transfer fluid containing a very small quantity of nanoparticles that are stably suspended in a carrier liquid. Fluids have typically very low thermal conductivity compared with crystalline solids. However, dispersion with small amount of solid nanoparticles in traditional fluid dramatically changes its thermal conductivities. The problem of heat transfer enhancement was first sorted out by Choi (1995) upon inventing “nanofluid” indicating engineered colloids composed of nanoparticles dispersed in a base fluid. The nanoparticles used in nanofluids are typically made of metals, oxides, carbides, nitrides, and nonmetals. The nanoparticles shapes may be spheres, disks, or rods (Rao 2010). In nanofluid, the base fluid is usually a conductive fluid, such as water or ethylene glycol. Other base fluids are oil and lubricants, bio-fluids, and polymer solutions. The subject of heat transport through dilute suspensions of solid particles has received a renewed boost owing reports of enhancement in thermal conductivity of suspensions carrying nanoparticles. The experimental studies have shown that the enhancement in thermal conductivity of nanofluids is determined by the parameters related to different nanoparticles, concentration, size (Patel et al. 2003; Xie et al. 2002; Chon et al. 2005), shapes (Eastman et al. 2001; Xie et al. 2002, 2003; Choi et al. 2001), agglomeration (fractal-like shapes) (Das et al. 2003; Lee et al. 1999; Xuan and Li 2000; Lee 2007), surface charge (Lee et al. 2006), base fluids, and others. The theory of spherical and non-spherical particles in nanofluid is of great interest in various engineering applications because of their much higher effective thermal conductivities over those of base liquids at very low particle volume concentrations. Poulikakos and coworkers (2010) carefully studied the effect of particle size, concentration, method of stabilization, and clustering on thermal transport in gold nanofluid. A maximum enhancement of 1.4 % was reported for volume 0.11 % suspension of 40-nm-diameter particles in water suggesting no apparent anomaly. Typical thermal conductivity of spherical particles enhancements is in the range 15–40 % over the base fluid and heat transfer coefficient enhancements have been found up to 40 % (Yu et al. 2008). In the literature, different authors investigate the thermal properties of cylindrical structures nanoparticle, namely single or multiwall nanotubes suspensions in a variety of solvents (Eastman et al. 2004; Fan and Wang 2011; Keblinski et al. 2008; Kleinstreuer and Feng 2011). Owing to different aspect ratios, solvents, and type of nanotubes (single or multiwall), there is considerable spread in the data. The reported values range from 10 % to over 150 % enhancement in the thermal conductivity for 1 volume 1 % concentration. Singh and coworkers (Singh et al. 2009) studied heat transfer behavior of aqueous suspension of silicon carbide having oblate shape and aspect ratio of around 1/4. They typically observed 30 % enhancement for volume 7 % concentration. Khandekar et al. (2008) employed various spherical nanoparticle as well as Laponite JS (oblate shape, aspect ratio 1/25) based nanofluids in closed two-phase thermosphere and observed its heat transport behavior to be inferior to that of pure water in all cases.

Moreover, porous media are used to transport and store energy in many industrial applications, such as heat exchangers, electronic cooling, heat pipe, solid matrix, and chemical reactors. In particularly, an important characteristic for the combination of the fluid and the porous medium is the tortuosity which represents the hindrance to flow diffusion imposed by local boundaries or local viscosity (Vafai 2011; Vafai and Kim 1989). Furthermore, mixed convection has various applications including cooling system for electronic devices, chemical vapor deposition instrument, furnace engineering, solar energy collectors and building energy system, non-Newtonian chemical processes and domains affected by electromagnetic fields, etc. The convective heat transfer mechanism of nanofluids and porous medium has been the subject of many studies for a better understanding of the associated transport processes. A large number of research work related to the said topics have been conducted by a number of investigators but the studies of mixed convection using nanofluids are very limited. Some relevant studies on the topic can be seen from the list of references (Akbar et al. 2013; Nadeem and Maraj 2014; Nadeem et al. 2013; Sheikholeslami et al. 2014a; b, c, d; Othman et al. 2014; Othman and Zaki 2004; Ibrahim et al. 2009).

Furthermore, a characteristic flow configuration having fundamental importance is that of the flow over a wedge. This type of flow constitutes a general class of investigations in fluid mechanics in which the free stream velocity is proportional to the power of length coordinate measured from the stagnation point. The two-dimensional incompressible wedge flows studied, for the first time by Falkner and Skan (1931). Since then, many authors confined their work in this regime, for instance, Watanabe et al. (1994) have presented the behavior of the thermal boundary layer over a wedge with suction or injection in a mixed convection flow. Heat transfer characteristics in forced convection flow over a wedge subjected to uniform wall heat flux are studied by Yih (1998). Kumari et al. (2001) have investigated the mixed convection flow over a vertical wedge embedded in a highly porous medium, whereas heat transfer analysis on Falkner–Skan wedge flow using differential transformation method is reported by Kuo (2005). The most recent and representative research work, for this type of flow, is presented in Ganapathirao et al. (2013) and several reference can be seen therein.

The core determination of the present work is to examine the shape effects of nanofluid over a wedge by considering the spherical and non-spherical shapes with different sizes of nanoparticles under the influence of nanolayer which has not been yet studied. The HFE-7100, HFE-7200, and HFE-7500 Engineered Fluids which are non-flammable fluid having very low global warming potential in heat transfer applications are used as based fluids. In addition, Bejan number and entropy generation are also taken into account. Due to intrinsic nonlinearity of the governing equations, analytical solutions are very rare. To deal with this difficulty, numerous analytical and semi-analytical methods have been established. The “homotopy analysis method” is one of most effective techniques among them to handle this obstacle. In this paper, the solutions of nonlinear resulting equations are carried out using Mathematica package BVPh 2.0 (Zhao and Liao 2013) which is based on homotopy analysis method (HAM). This method is particularly suitable for strongly nonlinear problems (Liao 2003, 2012; Ellahi 2013). The results for velocity, temperature, Bejan number, and Entropy generation are shown in the form of graphs, whereas the tabular results are displayed for heat transfer rate and Skin friction. After the “Introduction” section, the outlines of this paper are as follows. “Mathematical formulation of the problem” section contains mathematical formulation. In “Entropy generation analysis” and “Solution of the problems” sections, Entropy generations analysis and solutions of the problems are presented, respectively. Results and discussion is given in fifth section. Finally, “Conclusions” section summaries the concluding remarks.

Mathematical formulation of the problem

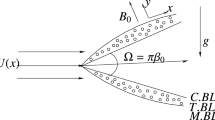
The steady two-dimensional, incompressible nanofluid flow over a wedge is considered. The wedge is submerged in mixed convective heat transfer and Newtonian fluid (air) flowing with the velocity u e(x) = ax m in which constant m = β*/2 − β* (see Kafoussias and Nanousis 1997). If β* < 0, the flow is decelerated, which means that an adverse pressure gradient is imposed, whereas for β* > 0, the flow is accelerated or a favorable pressure gradient is imposed. The fluid on the wedge is subjected to suction or blowing through the entire surface or locally from slots on various locations on the surface of the wedge. The suction/injection velocity on the wedge surface is v m, whereas the temperature of the surface of the wedge is T w(x). The HFE-7100 engineered fluid is considered as base fluid with Nimonic 80a metal nanoparticles of different shapes for nanofluid.

Under the above assumptions, the equations governing this type of flow can be written in the orthogonal system of coordinates shown in Fig. 1, as follows (Cebeci and Bradshaw 1984; Kafoussias and Xenos 2000). The governing equations for the continuity, momentum, and energy using the Boussinesq and the boundary-layer approximations along with the corresponding boundary conditions can now be written as

Fig. 1
figure 1

Configuration of the flow and geometrical coordinates

Full size image
$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = u_{\text{e}} \frac{{{\text{d}}u_{\text{e}} }}{{{\text{d}}x}} + \nu_{\text{nf}} \frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{{( {\rho \beta } )_{\text{nf}} }}{{\rho_{\text{nf}} }}g ({T - T_{\infty } })\,\sin \Upomega ,$$
(2)
$$\left( {\rho C_{\text{p}} } \right)_{\text{nf}} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) = k_{\text{nf}} \frac{{\partial^{2} T}}{{\partial y^{2} }},$$
(3)
$$\left. {\begin{array}{*{20}c} {u(x,0) = 0,\quad v(x,0) = v_{\text{w}} (x),\quad u\left( {x,\infty } \right) = u_{\text{e}} (x)} \\ {T(x,0) = T_{\text{w}} (x) = T_{\infty } + Cx^{m} ,\quad T\left( {x,\infty } \right) = T_{\infty}.} \end{array} } \right\},$$
(4)

where u and v are the velocity components in the x- and y-directions, respectively.

The suction/injection velocity distribution across the wedge surface is assumed to have the following function:

$$v_{\text{w}} = - f_{\text{w}} (\nu a)^{1/2} \left( {\left( {m + 1} \right)/2} \right)\,x^{{\left( {m - 1} \right)/2}} ,$$

where v w is the dimensionless wall mass transfer coefficient. When we choose v w > 0 velocity across the surface of the boundary wall, it shows the mass injection, and when chooses velocity of mass v w < 0, it shows mass suction process. The total angle of wedge is Ω = πβ*. T w and T ∞ is the temperature of wall and temperature of the ambient fluid. In Eqs. (1)–(3), the effective density ρ nf, heat capacitance (ρC p)nf, thermal expansion coefficient β nf, and thermal diffusibility α nf of the nanofluid are defined by

$$\rho_{\text{nf}} = \left( {1 - \phi } \right)\,\rho_{\text{f}} + \phi \rho_{\text{s}} ,$$
(5)
$$\left( {\rho C_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\,\left( {\rho C_{\text{p}} } \right)_{\text{f}} + \phi \left( {\rho C_{\text{p}} } \right)_{\text{s}} ,$$
(6)
$$\beta_{\text{nf}} = \frac{{\left( {1 - \phi } \right)\,\left( {\rho \beta } \right)_{\text{f}} + \phi \left( {\rho \beta } \right)_{\text{s}} }}{{\rho_{\text{nf}} }},$$
(7)
$$\alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}.$$
(8)

Here, \(\phi\) is the solid volume friction, β f and β s are respectively the thermal expansion coefficients of the base fluid and nanoparticle, ρ f and ρ s are the densities of basic fluid and nanoparticle, respectively. We will use the thermal conductive model for nanoparticles for spherical and non-spherical (Yu and Choi 2004) as follows:

$$k_{\text{nf}} = \left( {1 + \frac{{m\phi_{\text{e}} A}}{{1 - \phi_{\text{e}} A}}} \right)\,k_{\text{f}} ,$$
(9)

in which the parameter A is given by

$$A = \frac{1}{3}\sum \limits_{j = a,\,b,\,c} \frac{{k_{{{\text{p}}j}} - k_{f} }}{{k_{{{\text{p}}j}} + \left( {n^{ * } - 1} \right)\,k_{\text{f}} }}.$$
(10)

In above Eq. (10), n* = 3/ψ is the empirical shape factor (ψ is the sphericity defined as ratio between the surface area of the sphere and the surface area of the real particle with equal volumes), \(\phi_{\text{e}}\) is particle volume friction with nanolayer of base fluid on particle, k f is the thermal conductivity of base fluid, and k pj id thermal conductivity along the axes of the particle which is defined by

$$k_{{{\text{p}}j}} = \left[ {1 + \frac{{k_{\text{p}} - k_{\text{l}} }}{{k_{\text{p}} \left[ {r_{1} d\left( {j,\,0} \right) - d\left( {j,\,t} \right)} \right] - k_{\text{l}} \left[ {r_{1} d\left( {j,\,0} \right) - d\left( {j,\,t} \right) - r_{1} } \right]}}} \right]\,k_{\text{s}} ,$$
(11)

where j(= a, b, and c) is along the semi-axes direction of the particle, whereas k p and k l are the thermal conductivities of the solid particle and its surrounding layer, r 1 is the volume ratio and d(j,v) is depolarization factor defined by

$$r_{1} = \frac{{\sqrt {\left( {a^{2} + t} \right)\,\left( {b^{2} + t} \right)\,\left( {c^{2} + t} \right)} }}{abc},$$
(12)
$$\begin{aligned} d\left( {j,\,v} \right) &= \frac{{\sqrt {\left( {a^{2} + v} \right)\,\left( {b^{2} + v} \right)\,\left( {c^{2} + v} \right)} }}{2} \\ & \quad \times \int\limits_{0}^{\infty } \frac{{{\text{d}}w}}{{\left( {j^{2} + v + w} \right)\,\sqrt {\left( {a^{2} + v + w} \right)\,\left( {b^{2} + v + w} \right)\,\left( {c^{2} + v + w} \right)} }},\end{aligned}$$
(13)

with v = 0 for outside of solid ellipsoid and v = t for outside surface of its surrounding layer. For a needle-shaped particle with a = b ≫ c, d(a,v), d(b,v) and d(c,v) respectively tend to 0, 1/2, and 1/2 whereas for a disk-shaped particle d(a,v), d(b,v), and d(c,v) respectively tend to 0, 0, and 1, provided that a = b ≫ c. For a sphere with a = b = c, the three factors are 1/3. The effective viscosity models (Timofeeva et al. 2009) for nanofluid are given by as follows:

$$\mu_{\text{nf}} = 1 + A_{1} \phi + A_{2} \phi^{2} .$$
(14)

In the thermal conductive and viscosity models, the value of empirical shape factor n*, sphericity ψ, the values of A 1 and A 2 is shown in Table 1.

Table 1 The value of parameters for thermal conductive and viscosity models
Full size table

Physical properties of base fluid and particles are shown in Table 2.

Table 2 Physical properties of base fluid and particles for nanofluid
Full size table

In order to solve the system of PDEs, the compressible version of the Falkner–Skan transformation for a wedge (Kafoussias and Nanousis 1997) is introduced, defined by

$$\left. {\begin{array}{*{20}c} {\eta = \sqrt {\frac{{u_{\text{e}} \left( x \right)}}{{\nu_{f} x}}} y,\quad \psi = \sqrt {\nu_{\text{f}} xu_{\text{e}} (x)} f(\eta ),} \\ {\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{\rm w} - T_{\infty } }}} \\ \end{array} } \right\},$$
(15)

where ψ(x,y) satisfies the continuity equation.

The stream function is defined as

$$u = \frac{\partial \psi }{\partial y}\quad{\text{ and }} \quad v = - \frac{\partial \psi }{\partial x}.$$

Substituting into Eqs. (1)–(4), one can get the non-dimensional form of Eqs. (16) and (17) along with associated boundary conditions

$$\frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }}\left\{ {mf^{{{{{\prime }2}} }} - \left( {\frac{m + 1}{2}} \right)\,f^{{\prime \prime }} } \right\} = m + \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}f^{{{\prime \prime \prime }}} + \lambda { \sin }\left( {\varOmega /2} \right)\frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }}\theta,$$
(16)
$$\textit{Pr} \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{f}} }}\left\{ {mf^{{\prime }} \theta - \left( {\frac{m + 1}{2}} \right)\,f\theta^{{\prime }} } \right\} = \frac{{k_{\text{nf}} }}{{k_{f} }}\left( {\frac{m + 1}{2}} \right)\,\theta^{{\prime \prime }} ,$$
(17)
$$\left. {\begin{array}{*{20}c} {f(0) = f_{\text{w}} ,\quad f^{{\prime }} (0) = 0,\quad f^{{\prime }} (\infty ) = 1} \\ {\theta (0) = 1, \quad \theta (\infty ) = 0} \\ \end{array} } \right\},$$
(18)

in which

$$\textit{Pr} = \frac{{\nu_{\text{f}} }}{{\alpha_{\text{f}} }},\,\quad \lambda = \frac{Gr}{{\text{Re}^{2} }},\quad \,Gr = \frac{{\beta_{\text{f}} g\left( {T_{\text{w}} - T_{\infty } } \right)\,x^{3} }}{{\nu_{\text{f}}^{2} }},\quad Re = \frac{{u_{\text{e}} x}}{{\nu_{\text{f}} }},$$

where Pr is the Prandtl number, λ is the mixed convection parameter, Gr is the Grashof number, and Re is the Reynolds numbers.

The wall shear stress (Skin friction coefficient) can be expressed in demission less form as

$$C_{\text{f}} \text{Re}_{x}^{1/2} = 2\left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right)\,f^{{\prime \prime }} (0).$$
(19)

The local Nusselt number (heat transfer rate) is obtained in dimensionless form as follows:

$$Nu\text{Re}_{x}^{ - 1/2} = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\theta^{{\prime }} (0).$$
(20)

Entropy generation analysis

The local volumetric rate of entropy generation for a nanofluid flow (Butt and Ali 2013) is defined by

$$S_{\text{gen}} = \mathop {\underbrace {{\frac{{k_{\text{nf}} }}{{T_{\infty }^{2} }}\left( {\frac{\partial T}{\partial y}} \right)^{2} }}}\limits_{\text{HFI}} + \mathop {\underbrace {{\frac{{\mu_{\text{nf}} }}{{T_{\infty } }}\left( {\frac{\partial u}{\partial y}} \right)^{2} }}}\limits_{\text{FFI}} .$$
(21)

In Eq. (16), the first term HFI is the entropy generation due to heat transfer and the second term FFI is the entropy generation due to viscous dissipation. The dimensionless form of the entropy generation is given by

$$N_{\text{s}} = \frac{{S_{\text{gen}} }}{{S_{\text{o}} }} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}R_{\text{e}} \theta^{{{\prime }2}} + \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}\frac{{R_{\text{e}} Br}}{\omega }f^{{{\prime \prime }2}},$$
(22)

where \(S_{\text{o}} = k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)^{2} /T_{\infty }^{2} x^{2}\) is the characteristic entropy generation rate, \(\omega = \frac{{T_{\infty } }}{{T_{\text{w}} - T_{\infty } }}\) is the dimensionless temperature difference, Br = Pr Ec is the Brinkman number. In which, T w and T ∞ are measured in degree of Kelvin.

An alternative irreversibility distribution parameter is the Bejan number Be, which gives an idea whether the fluid friction irreversibility dominates over heat transfer irreversibility or the heat transfer irreversibility dominates over fluid friction irreversibility. It is simply the ratio of entropy generation due to heat transfer to the total entropy generation

$$Be = \frac{\text{HFI}}{{{\text{HFI}} + {\text{FFI}}}}.$$
(23)

when Be ≫ 0.5, the irreversibility due to heat transfer dominates, whereas when Be ≪ 0.5, the irreversibility due to viscous effects dominates. When Be = 0.5, the heat transfer and the fluid friction irreversibility are equal.

Solution of the problems

In this section, the analytical solutions of Eqs. (16) and (17) will be determined for the velocity and temperature profiles by using Mathematica package BVPh 2.0 which is based on the HAM. For simplicity, the BVPh 2.0 needs to input the governing equations along with corresponding boundary conditions and choose proper initial guess of solutions and auxiliary linear operators for under consideration linear sub-problems. In this package, one has great freedom to choose the auxiliary linear operator and initial guess, thus we choose the auxiliary linear operators and initial guess for the desire solutions as follows:

$$f_{0} \left( \eta \right) = - 1 + f_{w} + \eta + e^{ - \eta } ,\,\quad \theta_{0} \left( \eta \right) = e^{ - \eta }$$
(24)

as the initial approximation of f and θ, respectively, which satisfy the following linear operator and corresponding boundary conditions:

$$\pounds_{1} (f) = \left( {\frac{{{\text{d}}^{3} }}{{{\text{d}}\eta^{3} }} - \frac{\text{d}}{{{\text{d}}\eta }}} \right)\,f,\,\quad \pounds_{2} (\theta ) = \left( {\frac{{{\text{d}}^{2} }}{{{\text{d}}\eta^{2} }} - 1} \right)\,\theta .$$
(25)

Using the linear auxiliary operators in Eq. (25) and the initial approximations in Eq. (24), the coupled nonlinear Eqs. (16) and (17) subject to the boundary conditions given in Eq. (18), finally the solutions of velocity and temperature distributions can be expressed explicitly by an infinite series of the following form:

$$f_{i} \left( \eta \right) = \mathop {\mathop {\mathop \sum \limits }\limits_{m = 0} }\limits^{\infty } f_{i,\,m} \left( \eta \right),$$
(26)
$$\theta_{i} \left( \eta \right) = \mathop {\mathop {\mathop \sum \limits }\limits_{m = 0} }\limits^{\infty } \theta_{i,\,m} \left( \eta \right),$$
(27)

where \(f_{i,\,m} \left( \eta \right)\) and \(\theta_{i,\,m} \left( \eta \right)\) are governed by high-order deformation equations, which are linear and dependent upon auxiliary linear operators given in Eq. (25). We get the results for velocity, temperature distribution, Sink fiction, and Nusselt numbers for different non-dimensional numbers at 30th iterations of package.

The solutions for velocity and temperature up to second iteration are as follows:

$$\begin{aligned} f(\eta ) &= 1 + \left( {\begin{array}{*{20}c} { - 1 - \frac{{11A_{1} }}{30} + \frac{{187A_{2} }}{1440} + \frac{{209A_{2} m}}{288}} \\ { + \frac{{11A_{2} f_{\text{w}} }}{60} + \frac{11m\eta }{20} - \frac{{11A_{2} m\eta }}{20} + \frac{{11A_{3} \lambda }}{30}\sin \left( {\varOmega /2} \right)} \\ \end{array} } \right)\,e^{ - \eta } \\ &\quad + \left( {\begin{array}{*{20}c} {\frac{{11A_{1} }}{30} - \frac{{11A_{2} }}{180} - \frac{{143A_{2} m}}{180}} \\ { - \frac{{11A_{2} \eta }}{60} - \frac{{11A_{2} \eta f_{\text{w}} }}{60} - \frac{{11A_{2} m\eta }}{60} - \frac{{13A_{3} \lambda }}{30}\sin \left( {\varOmega /2} \right)} \\ \end{array} } \right)\,e^{ - 2\eta } + \left( {\begin{array}{*{20}c} {\frac{{ - 11A_{2} }}{160}} \\ { + \frac{{11A_{2} m}}{160}} \\ \end{array} } \right)\,e^{ - 3\eta } , \end{aligned}$$
(28)
$$\begin{aligned} \theta \left( \eta \right) &= \left( {\begin{array}{*{20}c} {1 + \frac{{13B_{1} }}{30} - \frac{{221B_{2} \textit{Pr} }}{1440} + \frac{{13A_{1} Ec\,\textit{Pr} }}{60}} \\ { - \frac{{611B_{2} m\,\textit{Pr} }}{1440} - \frac{{611B_{2} \,\textit{Pr}\, f_{\text{w}} }}{60} + \frac{{13B_{2} m\,\textit{Pr}\, f_{\text{w}} }}{60}} \\ \end{array} } \right)\,e^{ - \eta } \\ & \quad + \left( {\begin{array}{*{20}c} { - \frac{{3B_{1} }}{30} + \frac{{13B_{2} \,\textit{Pr} }}{180} + \frac{{91B_{2} m\,\textit{Pr} }}{180}} \\ { + \frac{{13B_{2} \,\textit{Pr}\, f_{\text{w}} }}{60} + \frac{{13B_{2} m\,\textit{Pr}\, f_{\text{w}} }}{60}} \\ { + \frac{{13B_{2} \,\textit{Pr}\, \eta }}{60} + \frac{{13B_{2} m\,\textit{Pr}\, \eta }}{60}} \\ \end{array} } \right)\,e^{ - 2\eta } + \left( {\begin{array}{*{20}c} {\frac{{13B_{1} }}{160} - \frac{{13A_{1} Ec\,\textit{Pr} }}{60}} \\ { - \frac{{13B_{2} m\,\textit{Pr} }}{160}} \\ \end{array} } \right)\,e^{ - 3\eta }, \end{aligned}$$
(29)

where

$$A_{1} = \frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }},\quad A_{2} = \frac{{\rho_{\text{nf}} }}{{\rho_{\text{f}} }},\quad A_{3} = \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\left( {\rho \beta } \right)_{\text{f}} }},\,\quad B_{1} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }},\quad B_{2} = \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}.$$
(30)

Results and discussion

In this section, the behavior of emerging parameters involved in the expression of velocity and temperature distributions is examined through Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 with HEF-7100 based nanofluids contained Nimonic 80a nanoparticles. The governing equation and their boundary conditions are transferred to ordinary differential equations. These equations include the nanoparticles volume friction \(\varphi,\) mixed convection parameter λ, suction or injection parameter f w, and total angle of wedge is Ω. In this study, for velocity and temperature profile, we prepare the particles of different shapes by applying the Eq. (10). We take spherical shape particle of 5 nm radius, needle shape of 5 nm radius and 50 nm length and disk shape of 50 nm radius and thickness of 5 nm. We also consider nanolayer thickness 2 nm of base fluid on particle and for this take the value t = 24. The thermal conductive of nanolayer k l is consider 2k f. These figures \(0\,\% \le \phi \le 10\,\%\) are prepared within range of particle volume friction and consider that heat is dominant in fluid. The effects of particle volume friction on velocity and temperature profiles are shown in Figs. 2 and 3, respectively. Figure 2 points out the velocity of fluid decreases by increasing the particle concentration. It is due to the fact that when particle concentrations become enlarge, the viscosity of fluid is enhanced. It is in accordance with the physical expectation since the fluid having low viscosity can easily move as compared to high viscosity fluid. It is also observed that the maximum velocity decreases for needle followed by disk and sphere shapes particles, respectively. On the other hand, in Fig. 3, the temperature profile increases for raising the particle volume friction. This is in accordance with the fact that temperature of fluid becomes enlarged when the thermal conductivity is elevated and as a result the thermal conductivity increases by increasing the particle volume friction. It is noticed that the maximum temperature of nanofluid increases for disk-shaped followed by the needle-shaped and sphere-shaped particles, respectively. Figures 4 and 5 show the effects of volume friction on velocity and temperature profile. To see the 3D impact, these figures are prepared for back replacing the transformations T ∞ = 295 K and ΔT = 80 K. Figures 6 and 7 show the behavior of non-dimensional mixed convection parameter λ on velocity and temperature profile of nanofluid. This parameter is ratio of buoyancy forces to the inertial forces inside the boundary layer for the laminar boundary layer forced-free convective flows. However, forced convection exists when the limit of λ tends to zero and the free convection limit can be reached if it becomes large. These figures depict that when the buoyancy force is increased, the velocity of the fluid is enhanced, whereas temperature is increased when boundary layer flow turn to free to force convection. The effects of suction or injection parameter on velocity and temperature are plotted in Figs. 8 and 9. When one chooses v w > 0, the velocity across the surface of the boundary wall, it means f w < 0 that is mass injection. When one chooses velocity of mass v w < 0, it means f w > 0 which shows mass suction. Figure 8 demonstrates the enhancement in velocity distribution in boundary layer region for the suction case. In Fig. 9, it is observed that the temperature is reduced when the value of f w is enlarged. Figures 10 and 11 illustrate the effects of angle of wedge on the non-dimensional velocity and temperature in the presence of spherical and non-spherical nanoparticles. As it is seen that when angle of wedge increases, the velocity profile is decreased as shown in Fig. 10. In addition, when angle of wedge increases, the temperature of nanofluid is declined.

Fig. 2
figure 2

Effect of volume friction on velocity profile

Full size image
Fig. 3
figure 3

Effect volume friction on temperature profile

Full size image
Fig. 4
figure 4

Effect of volume friction on velocity profile

Full size image
Fig. 5
figure 5

Effect of volume friction on temperature profile

Full size image
Fig. 6
figure 6

Effect of mixed convection parameter on velocity profile

Full size image
Fig. 7
figure 7

Effect of mixed convection parameter on temperature profile

Full size image
Fig. 8
figure 8

Effect of suction or injection parameter on velocity profile

Full size image
Fig. 9
figure 9

Effect of suction or injection parameter on temperature profile

Full size image
Fig. 10
figure 10

Effect of total angle of wedge on velocity profile

Full size image
Fig. 11
figure 11

Effect of total angle of wedge on temperature profile

Full size image

The effects of the particles volume friction on entropy generation number Ns are shown in Fig. 12. It is noticed from this figure that entropy production increases by increasing the particles volume friction. It is also observed that the irreversibility near the surface has maximum and then decreases and approaches to zero far from the disk. The maximum irreversibility is realized by disk-shaped particles when compared with other shapes (Fig. 13).

Fig. 12
figure 12

Effect of volume friction on entropy generation number

Full size image
Fig. 13
figure 13

Effects of particle volume friction on stream lines over a wedge. a Stream lines when \(\phi = 0\,\% ,\) b stream lines when \(\phi = 5\,\% ,\) and c stream lines when \(\phi = 10\,\%\)

Full size image

The numerically results in Tables 3, 4, 5, 6, and 7 illustrate the effects of various parameters on the skin friction coefficient, heat transfer rate of spherical and non-spherical nanoparticles suspended in HEF-7100 fluid. These tables are prepared by fixing the parameters λ = 2, f w = 2, and Ω = π/6. The effects of particle volume friction on the local skin friction coefficients and local Nusselt number are shown in Table 3. Table 3 depicts that with increasing the volume friction of nanoparticles suspension in the base fluid, both local skin friction coefficients and heat transfer rate increase, respectively. The maximum wall shear stress is caused by needle-shaped particle. Moreover, the maximum heat transfer rate is due to the disk-shaped particle. In addition, the heat transfer rate of HFE-7100 based nanofluid is improved 8.3, 24, and 13.3 corresponding to needle-shaped, disk-shaped, and sphere-shaped particle at 6 % of particle volume friction. The effects of particle’s size on skin friction coefficient and heat transfer are shown in Tables 4, 5, and 6. It is observed that the local skin friction as well as local Nusselt number decreases with the enhancement in length, radius of needle-shaped particles, thickness of disk-shaped particles and radius of sphere-shaped particles. It is also seen that the small size particles are more effective for heat transfer rate as compared to large size particle. For example, when one take spherical particle, the heat transfer rate is improved 11 and 10 % corresponding to radius of 5 and 30 nm at 5 % particle volume friction, respectively. To investigate wall shear stress and heat transfer rate, three different Novec-based fluids are examined in Table 7. It is found that the effect of wall shear stress maximum reduces by HFE-7500 fluid than other, while maximum enhanced in heat transfer rate is observed for HFE-7200 fluid as compared to rest of Novec fluids.

Table 3 Effect of volume friction on skin friction coefficient and Nusselt number
Full size table
Table 4 Effect of dimension of needle on skin friction coefficient and Nusselt number
Full size table
Table 5 Effect of dimension of disk on skin friction coefficient and Nusselt number
Full size table
Table 6 Effect of dimension of sphere on skin friction coefficient and Nusselt number
Full size table
Table 7 The values of skin friction coefficient and Nusselt number for different base fluids
Full size table

Conclusions

In this paper, the shape effect on HFE-7100 based nanofluid with influence of different parameters is investigated. It is observed that the velocity of nanofluid decreases by increasing the value of particle volume friction and angle of wedge. On the other hand, the velocity profile increases by increasing the values of mixed convection λ and suction (or injection) parameter. The temperature of nanofluid increases by increasing the volume friction. The temperature decreases due to enhancement in the effect of mixed convection parameter, suction (or injection) parameter, and angle of wedge. The lowest velocity and highest temperature of nanofluid are caused by the needle-shaped particles. The highest velocity and lowest temperature are determined by sphere particles. It is perceived that the entropy generation increases near the surface and then decreases and finally approaches zero near to free stream region. The maximum entropy production is found by the needle-shaped particles when it compared with the rest of shapes. The wall shear stress declines by increasing the size of particles. The minimum wall shear stress is seen for sphere-shaped particle and HFE-7500 base fluid. With the increase in volume friction and at small size of particle, the behavior of heat transfer rate increases. The maximum heat transfer is obtained when one chose disk-shaped nanoparticles and HFE-7500 fluid as compared to other. It is also found that small size particle and non-spherical shape are more stimulated for heat transfer rate.