Introduction

According to recent estimates, there are approximately 2 million oil wells worldwide of which about 50 % are placed on some kind of artificial lift (Lea 2007). The great majority of artificially lifted wells is produced by the age-old method of sucker-rod pumping. This is the reason why maintaining optimum operating conditions for such installations has great technical and economic benefits in providing energy resources to the world. The basic objective of operators is to produce wells using the least amount of total costs of which operating costs are crucial because of the ever-increasing cost of power.

Power costs in sucker-rod pumping operations are related to the surface power required to drive the pumping system. This power, in turn, depends mainly on the mechanical torque required at the gearbox of the pumping unit. Thus, proper calculation of gearbox torques during the pumping cycle is crucial for determining the power requirements and operating costs of sucker-rod pumping. Torques on the crankshaft of the gearbox are classified as static torques required to move the polished rod and the counterweights, and inertial torques representing the energy stored in and released from the accelerating/decelerating parts of the pumping unit (Takacs 2003).

Torques on the gearbox are found from the variation of the polished rod load during the pumping cycle; torque calculations, therefore, depend on the accurate measurement of those loads. These are obtained from a dynamometer survey which is the most valuable tool for analyzing the performance of the pumping system. Polished rod dynamometers, as the name implies, are instruments recording polished rod loads during the pumping cycle. The conventional dynamometer produces a continuous plot of polished rod load versus polished rod displacement, the so-called dynamometer diagram or card. Modern dynamometers, on the other hand, are electronic devices that record the loads and displacements at the polished rod in the function of time. Because of the operating differences of the two dynamometer types different procedures must be used to derive gearbox torques depending on the device used, as discussed in the following.

Fundamentals of gearbox torque calculations

When calculating gearbox torques on a pumping unit, two basic cases can be distinguished depending on the angular velocity of the crankshaft (a) those with a constant or nearly constant, and (b) those with varying crankshaft velocities. In the majority of pumping installations, the crankshaft’s angular velocity is constant during the pumping cycle and matches the measured pumping speed. These are the cases when the gearbox is properly counterbalanced and an electric motor with a low slip drives the pumping unit (Takacs 2003). The API Spec. 11E (API 2008) suggests that up to a speed variation of 15 % over the average pumping speed, neglecting inertial effects does not introduce errors greater than 10 % in torque calculations.

The API torque analysis

The API torque analysis model [published in the appendices of API Spec. 11E (API 2008) as a recommended calculation procedure] was developed for cases with a constant crankshaft velocity and can be applied to any class of pumping unit geometry. This calculation model uses the torque factor concept with the following basic assumptions

  • Frictional losses in the pumping unit structure are neglected, i.e., a torque efficiency factor of unity is used.

  • Inertial torques are neglected.

  • The change in structural unbalance, SU, with crank angle is also disregarded.

Under these conditions, the net torque acting on the gearbox is simply found from the sum of the rod torque and the counterbalance torque. For mechanically balanced pumping units, the following expressions are used for the different geometries

$$T_{\text{net}} \left( \theta \right)\; = \;\;T_{\text{r}} \left( \theta \right)\; - \;T_{\text{CB}} \left( \theta \right)\; = \;TF\left( \theta \right)\;\left[ {F(\theta )\; - \;{\text{SU}}} \right]\; - \;T_{\text{CBmax}} \;\sin \theta \quad {\text{Conventional}}$$
(1)
$$T_{\text{net}} \left( \theta \right)\; = \;\;\;T_{\text{r}} \left( \theta \right)\; - \;T_{\text{CB}} \left( \theta \right)\; = \;\;TF\left( \theta \right)\;\left[ {F(\theta )\; - \;{\text{SU}}} \right]\; - \;T_{\text{CBmax}} \;\sin \left( {\theta \; + \;\tau } \right)\,\quad {\text{Mark}}\,\,{\text{II}}$$
(2)
$$T_{\text{net}} \left( \theta \right)\; = \;\;\;T_{\text{r}} \left( \theta \right)\; - \;T_{\text{CB}} \left( \theta \right)\; = \;{\text{TF}}\left( \theta \right)\;\left[ {F(\theta )\; - \;{\text{SU}}} \right]\; - \;T_{\text{CBmax}} \;\sin \left( {\theta \; - \;\tau } \right)\,\quad {\text{Reverse Mark}}$$
(3)

The basic requirement for the calculation of gearbox torques is the knowledge of polished rod loads in the function of crank angle since rod torque is found by multiplying the load and the torque factor belonging to the same crank angle. This condition, however, is not met if data recorded on conventional dynamometer cards are used to find polished rod loads because these cards record the load against polished rod displacement. Thus the load versus crank angle function, F(θ), must be derived before the torques on the speed reducer can be calculated. The procedure introduced in API Spec. 11E (API 2008) and widely used for this purpose is based on data obtained from a conventional dynamometer survey.

Cases with variable crank speeds

When the pumping unit is driven by a multicylinder engine, a high-slip, or even an ultra-high-slip (UHS) electric motor, the angular velocity of the crankshaft changes during the pumping cycle: the crank speeds up when the unit is lightly loaded and slows down as the load becomes heavier. The high accelerations/decelerations coupled with the heavy rotating masses give rise to inertial torques because of the flywheel effect; gearbox torque calculations must be appropriately modified to include these effects. In such cases, in addition to the torques normally present on the gearbox and discussed so far, articulating and rotary inertial torques must be also calculated (Gibbs 1975).

Inertial torques

Articulating inertial torque exists even if the prime mover speed is constant and the crankshaft turns with a constant angular velocity. This torque is caused by those structural parts of the pumping unit that move with varying accelerations during the pumping cycle like the beam, horsehead, equalizer, etc. Since the net mass moment of inertia of the structural parts, I b, is usually supplied by the pumping unit manufacturer and the other parameters are provided by the pumping unit’s geometry, articulating inertial torque is basically a function of the walking beam’s angular acceleration, d2 θ b/dt 2, as shown in the following

$$T_{\text{ia}} \left( \theta \right)\; = \,\;\;\frac{12}{32.2}\;\,{\text{TF}}\left( \theta \right)\;\,\frac{{I_{\text{b}} }}{A}\;\,\;\frac{{{\text{d}}^{2} \theta_{\text{b}} }}{{{\text{d}}t^{2} }}.$$
(4)

Articulating inertial torque calculations, therefore, heavily depend on the proper determination of beam acceleration; the different solutions of which are detailed later.

Rotary inertial torque has a much greater importance than articulating torque. It can either increase or decrease the load on the gearbox. At times when crankshaft speed increases, the additional load (rotary inertial torque) on the gearbox is converted to kinetic energy and is stored in the rotating parts. On the other hand, if crankshaft speed decreases, then energy previously stored in the cranks and counterweights is returned into the system and the torque load on the gearbox is reduced. This interchange of kinetic energy happens in the following rotating masses of the pumping unit:

  • The cranks with crank pins,

  • The counterweights and auxiliary weights, and

  • The slow-speed shaft and slow-speed gear of the speed reducer.

Since all these components rotate around the crankshaft, their combined moment of inertia can be found from simple addition of the individual moments. Using the net moment of inertia of the rotating system, I s, the rotary inertial torque on the gearbox is found from the next formula

$$T_{\text{ir}} \left( \theta \right)\; = \,\;\;\frac{12}{32.2}\,\;I_{\text{s}} \;\,\;\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }}.$$
(5)

As seen, articulating inertia changes with the angular acceleration of the beam, d2 θ b/dt 2; while rotary inertial torque changes with the angular acceleration of the crankshaft, d2 θ/dt 2. Both of these can be derived from the angular velocity of the crankshaft, which, in turn, is the derivative of the crank angle versus time function, θ(t). The latter can be inferred from electronic dynamometer measurements using the calculation model developed in this paper and detailed later.

Net torque on the gearbox

In cases when the pumping system operates with varying crankshaft speeds, the net torque on the gearbox must include the inertial effects as well, and the formulas derived for a constant crankshaft speed (Eqs. 1–3) cannot be used. The proper formula for net torque is the algebraic sum of all possible torque components

$$T_{\text{net}} \left( \theta \right) = \;T_{\text{r}} \left( \theta \right)\;\; + \;\;T_{\text{CB}} \left( \theta \right)\;\; + \;\;T_{\text{ia}} \left( \theta \right)\;\; + \;\;T_{\text{ir}} \left( \theta \right)$$
(6)

Upon substitution into this equation of the relevant formulae introduced earlier, except for the expression for counterbalance torque, a generally applicable formula is found

$$T_{\text{net}} \left( \theta \right) = \;\;{\text{TF}}\left( \theta \right)\;\;\left[ {F\left( \theta \right)\;\; - \;\;{\text{SU}}\; + \;\frac{12}{32.2}\;\frac{1}{A}\;\;I_{\text{b}} \;\frac{{{\text{d}}^{2} \theta_{\text{b}} }}{{{\text{d}}t^{2} }}} \right]\;\; + \;\;T_{\text{CB}} \left( \theta \right)\;\; + \;\;\frac{12}{32.2}\;I_{\text{s}} \;\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}t^{2} }}.$$
(7)

The first term in this equation represents rod torque, corrected for articulating inertial effects, the second one stands for the counterbalance torque, and the last term gives the rotary inertial torque. The formula can be applied to any mechanically counterbalanced pumping unit after substitution of the proper expression for counterbalance torque, T CB(θ).

Determination of inferred crank angles

Introduction

As already discussed, gearbox torques are normally calculated based on dynamometer measurements that provide the variations of polished rod loads and positions. Modern dynamometer systems register these data in function of time but give no information on the crank angles valid at the measured times. This circumstance, however, prohibits a direct calculation of gearbox torques because all torque components depend on the crank angle, θ. Rod torque changes with the torque factor that varies with the crank angle; counterbalance torque is a direct function of crank angle, see Eqs. 1–3. Inertial torques are found from the acceleration patterns of different components of the pumping unit, these also change with the variation of the time history of crank angle. Gearbox torque components, therefore, can only be calculated if the change of crank angle with time, θ(t), is determined from dynamometer measurements.

Since direct calculation of crank angles from the measured polished rod positions is not possible, crank angles are inferred using the pumping unit’s kinematic parameters. This can be completed several ways, but all methods are based on setting the measured polished rod positions (acquired during a dynamometer survey) equal to the positions determined from the kinematic analysis of the pumping unit:

$$s\left( t \right)\; = \;S\;{\text{PR}}\left( \theta \right).$$
(8)

For each measured polished rod position, s(t), the corresponding crank angle, θ, is found when the above equation is satisfied; this procedure results in a series of crank angles in function of time, θ(t). This function, in turn, allows one to find the two important components of gearbox torque: rod and counterbalance torque. To calculate Rod Torque, the torque factor (TF) is found for each crank angle from the kinematic analysis of the pumping unit; torque is the product of the torque factor and the measured polished rod load. Counterbalance Torque, on the other hand, varies simply with the sine function of the crank angle. Determination of the inertial torque components, too, necessitates the knowledge of the crank angle-time function, θ(t), since both the angular acceleration pattern of the beam, d2 θ b/dt 2, and the angular acceleration of the crankshaft, d2 θ/dt 2, change with the variation of the crank angle.

Calculation procedure

The determination of the crank angle versus time function, θ(t), is accomplished according to the calculation model described on the flowchart presented in Fig. 1. After the input of the pumping unit’s main data (geometry type, dimensions, direction of rotation) and assuming a sufficiently small crank-angle increment, Δγ, the polished rod’s stroke length, S, and the starting crank angles of the up-, and the downstroke, θ u, θ d, respectively, are determined. These variables are evaluated according to the formulas recommended in API Spec. 11E (API 2008) for the calculation of the kinematic parameters of pumping units.

Fig. 1
figure 1

Flowchart of inferred crank angle versus time calculation

Full size image

Based on the measured polished rod positions, s(i), one can calculate the appropriate dimensionless positions:

$${\text{PR}}_{\text{m}} \left( i \right)\; = \;\frac{s\left( i \right)}{S}\;.$$
(9)

The objective of the main part of the calculation process is to find for each PRm(i) value the crank angle, θ, at which the position of rod function, PR(θ), a basic kinematic parameter of the pumping unit is equal to PRm(i). In the calculation procedure described in Fig. 1 the required iterative solution is executed by successive approximations using two auxiliary angles γ 1 and γ 2 being apart from each other by the assumed crank-angle increment, Δγ. At these angles, position of rods functions, PR(γ 1) and PR(γ 2), are evaluated using the API kinematic model for pumping units (API 2008). Using successive increments of the crank angle, the solution will fall between two consecutive angles γ 1 and γ 2 if the following expression becomes negative:

$${\text{diff}}\; = \;\left[ {{\text{PR}}\left( {\gamma_{1} } \right)\; - \;{\text{PR}}_{\text{m}} \left( i \right)} \right]\;\; \times \;\;\left[ {{\text{PR}}\left( {\gamma_{2} } \right)\; - \;{\text{PR}}_{\text{m}} \left( i \right)} \right].$$
(10)

Because of the small crank-angle increment used in the program (Δγ = 0.1°), linear approximation can be applied to find the crank angle that satisfies Eq. 9, i.e., θ(i) = (γ 1 + γ 2)/2. The error committed by using this approach is less than half of the increment used, i.e., Δγ/2, which is more than sufficient for the purpose.

The calculation model just described solves the basic problem of calculating gearbox torques by providing the variation of crank angles with time during the pumping cycle based on measured dynamometer data. The crank angle versus time function, θ(t), thus determined is used for the calculation of the angular acceleration of the crankshaft as well as that of the beam, as detailed in the following.

Calculation of angular accelerations

An example problem

As already discussed, inertial torques on the gearbox depend on the angular accelerations of the different components of the pumping unit. Since the determination of the angular accelerations of the crank and the beam from the crank angle versus time function, θ(t), necessitates several considerations, the solutions applied in this paper will be illustrated through an example problem. The sample well is produced with a 1.5″ pump set at 8000 ft and using a two-taper API 76 rod string. The surface pumping unit is a conventional C-640D-365-168 unit running in the clockwise direction at an average pumping speed of 5.98 SPM using a polished rod stroke length of 168 in. Linkage dimensions of the pumping unit (defined in Fig. 2) are given here:

Fig. 2
figure 2

Linkage dimensions of a conventional pumping unit

Full size image

A (in.)

210.00

K (in.)

192.87

I (in.)

120.00

C (in.)

120.03

P (in.)

148.50

R (in.)

47.00

The dynamometer survey contained 302 pairs of polished rod load, F(t), and position, s(t), data measured in function of time using an electronic dynamometer; the dynamometer card constructed from those data is presented in Fig. 3.

Fig. 3
figure 3

Dynamometer card for the example problem

Full size image

Crank angular acceleration

First, the crank angle versus time function, θ(t), is inferred from the data of the dynamometer survey using the calculation procedure described previously. Were the pumping unit’s crank turning at a constant speed, crank angles would fall on a straight line in function of time. In the example, however, this is not the case as shown in Fig. 4 and indicated by the deviation of the crank angle versus time function, θ(t), from the ideal straight line. This is caused by a varying pumping speed during the pumping cycle.

Fig. 4
figure 4

Calculated crank angles, speeds, and accelerations for the example case

Full size image

Angular velocity of the crank, dθ/dt, is the derivative of this function and is found by a numerical differentiation model using a five-step stencil as given here

$$\frac{{{\text{d}}\theta }}{{{\text{d}}t}}\,\; \approx \;\frac{{ - \theta \left( {t\; + \;2\,\Delta t} \right)\; + \;8\,\,\theta \left( {t\; + \,\Delta t} \right)\; - \;8\,\,\theta \left( {t\; - \;\Delta t} \right)\; + \;\theta \left( {t\; - \;2\,\Delta t} \right)\;\;}}{12\;\Delta t}.$$
(11)

To apply this model, two extra points (crank angles) at each end of the pumping cycle are required; these are estimated by straight-line extrapolations of the input data. This solution ensures that the derivative function does not have unusual peaks at the two ends of the cycle; calculation accuracy is provided by the small time increment. As shown in Fig. 4, the numerical differentiation results in a smooth curve for the crank angular velocity. Being a periodic function in time, it can be curve-fitted by a truncated Fourier series which is easy to differentiate to get the angular acceleration of the crankshaft, d2 θ/dt 2. Complete results of the calculation model developed in this paper for the example case are shown in Fig. 4 that depicts the variations of the crank’s angular velocity and acceleration with time to be used in subsequent calculations.

Calculation of the beam’s angular acceleration

Svinos’ kinematic model

The walking beam’s angular acceleration pattern can be derived from the pumping unit’s kinematic model, as suggested by Svinos 1983. Svinos used, instead of the crank angle, θ, defined in API Spec. 11E (API 2008), a different but related angle, θ 2, as the independent variable for his kinematic calculations. His formula for beam acceleration is given in Eq. 12; definitions of the angles figuring in the expression are shown in Fig. 2 that depicts the geometry of a conventional pumping unit according to API 2008.

$$\frac{{{\text{d}}^{ 2} \theta_{\text{b}} }}{{{\text{d}}t^{2} }}\; = \;\frac{{{\text{d}}\theta_{\text{b}} }}{{{\text{d}}t}}\;\left[ {\frac{{\frac{{{\text{d}}^{ 2} \theta_{2} }}{{{\text{d}}t^{2} }}}}{{\frac{{{\text{d}}\theta_{2} }}{{{\text{d}}t}}}}\; - \;\left( {\frac{{{\text{d}}\theta_{3} }}{{{\text{d}}t}}\; - \;\frac{{{\text{d}}\theta_{\text{b}} }}{{{\text{d}}t}}} \right)\;\cot \left( {\theta_{3} \; - \;\theta_{\text{b}} } \right)\; + \;\left( {\frac{{{\text{d}}\theta_{2} }}{{{\text{d}}t}}\; - \;\frac{{{\text{d}}\theta_{3} }}{{{\text{d}}t}}} \right)\;\cot \left( {\theta_{2} \; - \;\theta_{3} } \right)} \right].$$
(12)

The formula allows the calculation of beam accelerations for a general case when the pumping unit’s crank does not turn at a constant angular velocity, i.e., crank angular acceleration, d2 θ 2/dt 2, is not zero. As seen, the calculation requires the knowledge of the crank’s velocity and acceleration patterns, i.e., the dθ 2/dt and the d2 θ 2/dt 2 functions. These have to be determined previously, preferably using the iterative procedure introduced in this paper.

The use of the Svinos procedure just described is cumbersome for several reasons. Some additional angles and their time derivatives also are required to find beam acceleration; their formulas based on the linkage dimensions of the pumping unit are given by Svinos 1983, not reproduced here. Use of the iterative procedure to find the crank’s kinematic parameters complicates the solution and makes the otherwise straightforward procedure quite complicated to perform.

Gibbs’ proposal

A more direct calculation model was introduced by Gibbs 2012 based on Eq. 13 that expresses the polished rod’s position with the angular position of the beam’s centerline. The formula expresses the fact that the vertical displacement of the carrier bar (and the polished rod) equals to the length of the arc covered by the outward end of linkage A of the pumping unit for a given beam angle, θ b, see Fig. 2.

$$s\left( t \right)\; = \;A\;\theta_{\text{b}} \left( t \right)$$
(13)

Expressing the angle θ b from this formula and then differentiating the result twice with respect to time we receive

$$\;\frac{{{\text{d}}^{2} \theta_{\text{b}} \left( t \right)}}{{{\text{d}}t^{2} }}\; = \;\frac{1}{A}\;\frac{{{\text{d}}^{2} }}{{{\text{d}}t^{2} }}\,s\left( t \right).$$
(14)

This formula permits the direct calculation of the beam’s angular acceleration, d2 θ b/dt 2, by differentiation of the polished rod position—time data, s(t), obtained from a dynamometer survey. The easiest way to differentiate this function is to first fit the measured data series, s(t), with a truncated Fourier series and then find the second derivative of that. Because of the relatively smooth variation of polished rod position with time a maximum of ten terms in the Fourier series are recommended by Gibbs (2012).

A simple numerical model

A simple numerical model often used for calculating the kinematic parameters of pumping units (Echometer 2007) is based also on Eq. 14. Beam acceleration is found from the acceleration of the polished rod, represented by the term d2 s/dt 2 in the formula. Polished rod acceleration, in turn, is calculated from the polished rod position versus time values, s(t), measured during a dynamometer survey. Numerical differentiation of the function s(t) with respect to time gives polished rod velocity, v(t), as follows:

$$v\left( i \right)\; = \;\frac{{s\left( i \right)\; - \;s\left( {i + 1} \right)}}{{t\left( i \right)\; - \;t\left( {i + 1} \right)}}.$$
(15)

Polished rod acceleration, a(t), is found similarly by numerical differentiation of this function and the time history of the resultant acceleration provides the required d2 s/dt 2 values to be used in Eq. 14. Solving that equation gives the required values of beam acceleration, d2 θ b/dt 2.

Comparison of the available models

Figure 5 contains beam accelerations calculated from the Svinos and the simple numerical model for the example case. It is clearly seen that the numerical model’s general trend properly follows the accurate accelerations found from the kinematic model but instantaneous values fluctuate greatly making this approach to be of dubious value and to be excluded from further study.

Fig. 5
figure 5

Comparison of beam acceleration values calculated from the Svinos and the numerical model for the example problem

Full size image

Calculation results using the Gibbs model are given in Fig. 6. The figure displays the Fourier approximation (truncated at ten terms) of the polished rod displacement, as calculated from the s(t) function measured during the dynamometer survey. Thanks to the smooth nature of the polished rod displacement function, the fitting is excellent; polished rod velocity and acceleration are computed from the Fourier series by analytical differentiation. The figure depicts also the variations of polished rod velocity, ds/dt, and beam acceleration, d2 θ b/dt 2, the latter being calculated from Eq. 14. Comparison of Figs. 5 and 6 reveals that beam accelerations computed from the Svinos and Gibbs models give identical results; the complexity and calculation demand, however, of the two approaches are widely different. Because of its simplicity and low computation requirement the calculation model of Gibbs 2012 is recommended.

Fig. 6
figure 6

Calculated parameters from the Gibbs model for the example problem

Full size image

Calculated torques for the example problem

As discussed previously, the basic requirement for an accurate calculation of gearbox torque components from dynamometer survey data is the knowledge of the variation of crank angle versus time. The iterative procedure developed in this paper accomplishes this task by finding inferred crank angles from which the acceleration patterns of the pumping unit’s different parts are also found. All these kinematic parameters being available at this point, the calculation of torque components is straightforward. To illustrate the necessary calculations for the example problem, let’s find the gearbox torques at a time t = 1.0 s where the measured polished rod load is F(t) = 19,617 lb, and the crank angle calculated with the iterative procedure developed in this paper is θ(t) = 47.35°.

Rod torque is relatively simply found from the polished rod load recorded by the dynamometer, F(t), and the torque factor, TF(θ), derived from the crank angle, θ(t), using the formulas recommended in API Spec. 11E (API 2008). The unit’s structural unbalance is SU = −1500 lb, the torque factor calculated at the given crank angle is TF = 78.2 in; rod torque is found from Eq. 1, because the unit has a conventional geometry

$$T_{\text{r}} = 7 8. 2 \left( { 1 9, 6 1 7 + 1 500} \right) = 1 6 5 1\;{\text{k}}\;{\text{in}}\;{\text{lbs}}.$$

Articulating inertial torque is basically defined by the walking beam’s acceleration, which at the given time equals d2 θ b/dt 2 = −0.076 1/s2. The mass moment of inertia of the beam, horsehead, equalizer, bearings, and pitmans, referred to the saddle bearing, found from manufacturer data is I b = 1,047,183 lbm ft2 and the distance between the saddle bearing and the polished rod is A = 210 in. The torque is calculated from Eq. 4 as follows:

$$T_{\text{ia}} = 1 2/ 3 2. 2 \; 7 8. 2 \; 1,0 4 7, 1 8 3 / 2 10 \left( { - 0.0 7 6} \right) = - 1 1 \;{\text{k}}\; {\text{in}} \;{\text{lbs}}.$$

Counterbalance torque calculations necessitate knowledge of the current counterbalance conditions; the typical arrangement of counterbalance components is shown in Fig. 7. The maximum moment about the crankshaft is composed of the moments of the (a) cranks plus crank pins and (b) the counterweights plus auxiliary weights. The unit has 94110CA cranks whose maximum moment is T crank = 470,810 in lbs; the four ORO master weights weigh W = 3397 lb each, their maximum lever arm is M = 77.4 in, according to manufacturer data. There are no auxiliary weights used and the master weights are positioned at D = 10 in from the long end of the crank. The maximum counterbalance moment of the counterbalance components is found from the following (Bommer and Podio 2012)

Fig. 7
figure 7

Typical arrangement of a counterweight on the crank of a pumping unit

Full size image
$$T_{{{\text{CB}}\,\,{ \hbox{max} }}} = \;\;\;T_{\text{crank}} \; + \;\left( {M\; - \;D} \right)\;N\;W.$$
(16)

Using the data detailed above we get

$$T_{\text{CB max}} = 4 70, 8 10 + \left( { 7 7. 4 {-} 10} \right) \; 4 3, 3 9 7 = 1 3 8 7\; {\text{k}}\; {\text{in}}\; {\text{lbs}}.$$

Counterbalance torque at the given time is derived from Eq. 1, valid for a conventional geometry

$$T_{\text{CB}} = - 1, 3 8 7 { \sin }\left( { 4 7. 3 5} \right) = - 1,0 20 \;{\text{k}} \;{\text{in}} \;{\text{lbs}}.$$

Rotary inertial torque calculations start with the determination of the net mass moment of inertia of the pumping unit’s rotating parts, the individual components of which are the following:

$$I_{\text{s}} = \;\;I_{\text{cr}} \; + \;I_{\text{CW}} \; + \;I_{\text{g}} .$$
(17)

Since data on cranks and the slow-speed gearing (I cr and I g) is supplied by the manufacturer only the actual moment of inertia of the counterweight system must be found by calculation.

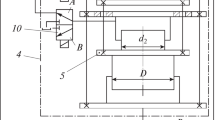
Figure 7 shows the principle of calculating the mass moment of inertia of counterweight components. If the moment of inertia of a single counterweight about its center of gravity (CG) is known then it can be referred to the crankshaft by using the Huygens–Steiner Theorem as follows

$$I_{\text{CW}} = \;\;I_{\text{CG}} \; + \;m_{\text{CB}} \;\left( \frac{H}{12} \right)^{2} .$$
(18)

The distance H changes with the position of the counterweight on the crank (see Fig. 7) and is easily found from

$$H = \;\sqrt {\left( {X\; + \;Y} \right)^{2} \; + \left( {M\; - \;D} \right)^{2} } .$$
(19)

The manufacturer supplied the moment of the cranks as I cr = 247,244 lbm ft2 with their dimension X = 11.5 in and the moment of the slow-speed shaft and gear as I g = 4400 lbm ft2. The moment of inertia for one counterweight about its center of gravity is I CG = 8017 lbm ft2, its dimension Y = 19 in.

Distance H is defined by Eq. 19 as

$$H = \left[ {\left( { 1 1. 5 + 1 9} \right)^{ 2} + \left( { 7 7. 4 {-} 10} \right)^{ 2} } \right]^{0. 5} = 7 3. 9 8 {\text{in}}.$$

Mass moment of inertia of the four ORO counterweights, according to Eq. 18:

$$I_{\text{CW}} = 4 \left[ { 8,0 1 7 + 3, 3 9 7 \left( { 7 3. 9 8/ 1 2} \right)^{ 2} } \right] = 5 4 8, 5 10 \,{\text{lb}}_{\text{m}} {\text{ft}}^{ 2} .$$

The system’s net mass moment of inertia is the sum of all inertias, Eq. 17

$$I_{\text{s}} \, = \, 2 4 7, 2 4 4 + 5 4 8, 5 10 + 4 400 = 800. 2 \;{\text{k}} \;{\text{lb}}_{\text{m}} {\text{ft}}^{ 2} .$$

The rotary inertial torque is found from Eq. 5 using the crank acceleration of d2 θ/dt 2 = −0.439 1/s2 at the given time:

$$T_{\text{ir}} = 1 2/ 3 2. 2\; 800, 200 \left( { - 0. 4 3 9} \right) = - 1 30. 9\; {\text{k}} \;{\text{in}}\; {\text{lbs}}.$$

Finally, the net gearbox torque at the time investigated is the sum of the four torque items just calculated:

$$T_{\text{net}} = 1 6 5 1 {-} 1 1 - 10 20 - 1 30. 9 = 4 8 9\; {\text{k}} \;{\text{in}}\; {\text{lbs}}.$$

The calculated variation of major torques (Rod, Counterbalance and Net Torques) for the complete pumping cycle is presented in Fig. 8. It is clearly seen that the gearbox is not properly counterbalanced because it is more loaded during the upstroke than the downstroke, as indicated by the two horizontal dashed lines representing the gearbox torque capacity. Inertial torques are plotted in Fig. 9; articulating inertial torque is not significant as compared to rotary inertial torque. The latter very substantially reduces the torque load on the gear reducer whenever its sign is negative. Negative rotary torque indicates that energy stored in the heavy rotating parts of the pumping unit is released and helps reducing the net torque. This behavior is caused by the great variation of crankshaft speed during the pumping cycle, already observed in Fig. 4.

Fig. 8
figure 8

Variation of rod, counterbalance, and net torques during the pumping cycle for the example case

Full size image
Fig. 9
figure 9

Variation of inertial torques during the pumping cycle for the example case

Full size image

Conclusions

Based on a detailed analysis of gearbox torque calculations the following conclusions were drawn that help improve the determination of the torque load from dynamometer survey data

  • When electronic dynamometers are used to analyze the operation of the sucker-rod pumping system then calculation of gearbox torques is only possible if the change of crank angle with time, θ(t), is inferred from dynamometer measurements.

  • The iterative procedure developed in the paper provides an accurate description of the variation of the crank angle with time from the data of a dynamometer survey.

  • The combination of numerical differentiation and the use of Fourier series, as described in the paper, yields the necessary angular accelerations of the crankshaft and the beam; these are used to find inertial torque components.

  • Because of its lower complexity and lower calculation requirement, the model proposed by Gibbs (2012) is recommended to find the angular acceleration of the beam.