Introduction

The analysis of the extreme values in climatological time series is an area of intense scientific activity. The annual or monthly maximum precipitation or temperature series are the examples of this type of data. The generalized extreme value (GEV) distribution is widely employed for modeling the extreme precipitation in the environmental sciences and many other fields (Reiss and Thomas 2007; Li-Ge et al. 2013; Ngailo et al. 2016; Boudrissa et al. 2017). The assumption of independent and identically distributed data in the series with constant properties through time (stationarity) may need to be modified to reflect climate change (non-stationarity). For example, the maximum temperature and precipitation series could show trends over time (Panagoulia et al. 2014). Furthermore, due to natural climate variability or anthropogenic climate change, there is evidence that the hydroclimatic extreme series are not stationary (Shaleen and Lall 2001; Milly et al. 2008). Many studies have analyzed extreme precipitation using either generalized GEV distribution which provides evidence of the importance of modeling precipitation from different regions of the world (Buishand et al. 2008; Carreau et al. 2013; Ender and Ma 2004). From example, Koutsoyiannis and Baloutsos (2000) applied to Greece’s rainfall data set. Crisci et al. (2002) applied extreme value distributions to rainfall data set from Italy. Koutsoyiannis (2004) applied extreme value theory to rainfall data set from Europe and USA. O’Gorman (2015) analyzed precipitation extremes under climate change. The observational and statistical modeling results of the different studies have shown that there are remarkable increases in intensity of precipitation extremes. However, there has been little or no published research that has attempted to detect extreme precipitation by using GEV in regions of Algeria. Therefore, this paper would seem to be the first application of the GEV distributions for extreme precipitation in Algeria.

In this study, we analyze the annual maximum precipitation data from 1969 to 2011 in five stations in Oued El Gourzi Watershed, Algeria. Three GEV models are proposed to fit the annual maximum precipitation for each station. Then, we have compared the different fitted models and selected the best model based on the Akaike’s information criterion (AIC) and Bayesian information criterion (BIC).

The paper is organized as follows. The annual maximum precipitation data are described in “Study area and precipitation data set” section. The models and the fitting procedure are described in “Statistical modeling” section. In “Conclusion” section, the results of the fitted models and their implications are discussed. The yearly return level estimates for the 20 and 100 years are reported.

Materials and methods

Study area and precipitation data set

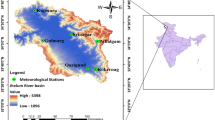
Oued El Gourzi Watershed is part of the great watershed of the Constantine’s Highlands in northeastern Algeria (Fig. 1). It is 400 km east of Algiers, between 6° 01′ 44″ and 6° 21′ 15″ east longitude and between 35° 25′ 57″ and 35° 36′ 33″ north latitude. It covers almost an area of 315 km2. Oued El Gourzi is of great importance in the Hydrographic system, fed by five main tributaries which are Oued Tazoult Southwest, Oued Azzeb and Oued Bouadane northwest, Oued Seguene northeast and Oued Hamla southeast; the studied basin takes these sources from the subsequent mountains. In the north, Dj Boumerzoug with an altitude of 1692 m, Dj Kassrou (1641 m), the northeast is occupied by Dj Azzab (1365 m) and Dj Bouarif (1584 m), the western part is dominated by Dj Tugurth (2091 m) and Dj Boukezzaz (1783 m), whether the south is occupied by Dj Ich Ali, whose altitude is about 1800 m, flows into the plain by Oued El Gourzi. The town of Batna located at the outlet of the Oued El Gourzi with a large population. Batna city recorded for the year 1995, 236,669 inhabitants, the largest rate of urbanization of the wilaya (89.4%) (Sefouhi et al. 2010). In addition, the population density is about 2050 Hab/km2 (The basic population data were collected from the last census of April 16, 2008).

Fig. 1
figure 1

Geographical map of the Oued El Gourzi Watershed and the five stations

Full size image

Annual maximum precipitation (AMP) data in Oued El Gourzi Watershed for the time period 1969–2011 were obtained from the National Agency of Hydraulic Resources (NAHR). In this study, we selected five stations: Ali Ben Tenoun (ABT), Batna (BAT), Hamla (HAM), Seguene (SEG) and Tazoult (TAZ) (Fig. 1). The statistical properties of annual maximum precipitation series of each station along with their geographic location are shown in Tables 1 and 2.

Table 1 Coordinates of the selected stations
Full size table
Table 2 Different combinations and the regression function
Full size table

Statistical modeling

Generalized extreme value (GEV) distribution

The GEV distribution is widely employed for modeling extremes in the environmental sciences and elsewhere (Reiss and Thomas 2007). It depends on location (µ), scale (σ) and shape (ξ) parameters. The generalized extreme value (GEV) distribution is a flexible three-parameter model that combines the Gumbel (ξ = 0), Fréchet (ξ > 0) and Weibull (ξ < 0) extreme value distributions. In the stationary GEV distribution, the three parameters are constant, while, in the non-stationary GEV distribution (El Adlouni et al. 2007; Leclerc and Ouarda 2007), these parameters are expressed as a function of time t and possibly other covariates (Coles 2001). If, as is usually done, we allow non-stationarity of the location and scale parameters but not of the shape parameter, this non-stationary GEV(µ(t), σ(t), ξ) distribution has distribution function:

$$F\left( {y;\mu \left( t \right),\sigma \left( t \right),\xi } \right) = \exp \left\{ { - \left[ {1 + \xi \frac{y - \mu \left( t \right)}{\sigma \left( t \right)}} \right]^{ - 1/\xi } } \right\}.$$
(1)

In the case of non-stationary, the following regression structures could be considered for the location and scale parameters:

$$\mu \left( t \right) = \mu_{0} + \mu_{1} \times t$$
(2)
$$\sigma \left( t \right) = \sigma_{0} + \sigma_{1} \times t$$
(3)

Allowing up to linear dependence on time of both the location and scale parameters, we denote by GEV(i, j, 0) the model with time dependence of order i in the location parameter and order j in the scale parameter. For example, the stationary GEV distribution is GEV(0, 0, 0), obtained when the location and scale parameters are both independent of time (μ1 = σ1 = 0), while the GEV(1, 1, 0) non-stationary model assumes a linear trend in location and scale. Two models of varying complexity may be defined in this way (two choices for each of i and j). Table 2 shows the different GEV models and their parameters.

We followed the recommendation in the program documentation to standardize covariates. Thus, the linear term in time is actually entered into the model as

$$x_{i} = \frac{{t_{i} - m}}{s}$$
(4)

where m and s are the mean and the standard deviation of the time covariate, respectively.

Model selection

The stationary and non-stationary GEV models may be fitted to a time series {y(ti): ti ∈ T} where T = {t1, t2,…, tn} by maximizing the log-likelihood function as follows:

$$\ell = \log L = \sum\limits_{i = 1}^{n} {\left( { - \log \left( {\sigma \left( {t_{i} } \right)} \right) - \left( {1 + \frac{1}{\xi }} \right)\log \left( {1 + \xi \frac{{y\left( {t_{i} } \right) - \mu \left( {t_{i} } \right)}}{{\sigma \left( {t_{i} } \right)}}} \right) - \left[ {1 + \xi \frac{{y\left( {t_{i} } \right) - \mu \left( {t_{i} } \right)}}{{\sigma \left( {t_{i} } \right)}}} \right]^{ - 1/\xi } } \right)} .$$
(5)

The goodness of fit and the significance of the models were tested with the aid of log-likelihood ratio test (LRT; Sienz et al. 2010), Akaike’s information criterion (AIC; Akaike 1974) and the Bayesian information criterion (BIC; Schwarz 1978). LRT, AIC and BIC methods are used to choose the best model at each station. The corrected AIC (AICc; Burnham and Anderson 2002) is used to select the best model for a small sample [(n/k) < 40]. If \(\hat{\ell }\) is the maximized value of the likelihood for a model containing p parameters and n is the sample size, the criteria are defined as

(the third term is the correction) and

$${\text{AIC}}_{\text{c}} = - 2\hat{\ell } + 2p + \frac{{2p\left( {p + 1} \right)}}{n - p - 1}$$
(6)
$${\text{BIC}} = - 2\hat{\ell } + p\log n.$$
(7)

The preferred model among the GEV models is the one that minimizes the chosen criterion, although attention should also be paid to models with values close to the minimum.

All results reported in this work were obtained in the R computing environment (R Development Core Team 2019), using the fevd routine in the extRemes package (Gilleland and Katz 2016) to fit stationary and non-stationary GEV distributions by maximum likelihood.

Results and discussion

Statistical descriptive of the annual maximum precipitation data

The preliminary analysis of the annual maximum precipitation data included the calculation of descriptive statistics. Specifically, we computed minimum (Min), maximum (Max), median, mean, standard deviation (SD) and coefficient of variation (Cv). Table 3 presents the values of the descriptive statistics for the annual maximum precipitation time series for all the stations. Figure 2 shows the boxplot of the annual precipitation for each station, and the graphical presentation of the temporal variability of precipitation for each station is shown in Fig. 3. The results show that the maximum value of AMP is observed in TAZ station, while the highest mean and median values are observed in SEG station (Fig. 2). The lowest value of Cv is for BAT station (35%) and the highest for TAZ station (65%). According to Hare (2003), coefficient of variation is used to classify the degree of variability of annual maximum precipitation as less (Cv < 20%), moderate (20% < Cv < 30%), high (Cv > 30), very high Cv > 40% and Cv > 70% indicate extremely high variability of annual maximum precipitation (Table 3 and Fig. 3). Based on this, from the observed data considered that all the stations had above 30% coefficient of variation highlighting the high variability of annual maximum precipitation over the Oued El Gourzi Watershed (Table 3 and Fig. 3).

Table 3 The characteristics of the annual maximum precipitation in the analyzed period
Full size table
Fig. 2
figure 2

Boxplot of the annual maximum precipitation

Full size image
Fig. 3
figure 3

Graphical presentation of the annual maximum precipitation for each station

Full size image

In order to understand the relationship between temperature and precipitation, the ombrothermal diagram of Bagnouls and Gaussen for Batna station (BAT) is used (Fig. 4). This diagram is presented by plotting on the abscissa axis, the months of the year, and on the ordinate the precipitation on the right and the average temperatures on the left (P = 2T) (Bagnouls and Gaussens 1953). From Fig. 4, we see clearly that the wet period ranges from November to May (7 months) for the study area.

Fig. 4
figure 4

Ombrothermal diagram of Bagnouls and Gaussen for Batna station (BAT)

Full size image

Preliminary analysis

As a first approach to study trends in annual maximum precipitation during the study period 1969–2011, the Mann–Kendall trend test is applied. A trend is considered to be present if it has been detected by the test. The results show that at the 0.05 significance level, the annual maximum precipitation series of ABT and TAZ stations exhibited a statistically significant trend, while the other stations did not have any statistically significant trend when we considered the entire study period (Table 4 and Fig. 5).

Table 4 Mann–Kendall trend test for each station
Full size table
Fig. 5
figure 5

Plot of annual maximum precipitation data for 1969 to 2011 with trend fitted by lowness smoother

Full size image

Comparison of selection criteria

We investigated the use of the GEV distribution to model the annual maximum precipitation in Oued El Gourzi Watershed. We modeled these events using both stationary and non-stationary models for the time period 1969–2011. The effect of time is taken into account. In this study, three GEV models are proposed. The parameter estimates and goodness-of-fit criteria tests (AICc and BIC) were calculated for different GEV models, as shown in Table 5. The best model was chosen based on the minimum values of GOF criteria. From the results, we see that the model 2, whose location parameter depends on time and whose other parameters are constant, is the best model for explaining change in the annual maximum precipitation at ABT and TZA stations. The model 0 (stationary case), where there are no significant trends, is the best model for the other stations. These findings are supported by Fig. 6, where we have shown the quantile and density plots of the fits for the five-time series. Figure 6 shows that the fit provided by model 0 and model 1 is good in this study area.

Table 5 Parameter estimates and summary of goodness-of-fit tests for three models
Full size table
Fig. 6
figure 6

Quantile and density plots for each station

Full size image

From Table 5, we see clearly that the location and scale parameters are high for SEG station. An analysis of the shape parameter obtained for all of the models and all of the stations except BAT station shows that this parameter is positive. A greater absolute value of this parameter corresponds to a greater annual extreme precipitation.

Return level estimates

Once the best model for the data has been determined, the interest is to derive the return levels of annual maximum precipitation. The T year return level, say xT, is the value occurring on average once in every T years. For example, the 2-year return level is the median of the distribution of each station. If the model 1 is assumed, then on inverting \(F\left( {x_{T} } \right) = 1 - \frac{1}{T}\) we get:

$$x_{T} = \mu - \frac{\sigma }{\xi }\left[ {1 - \left\{ { - \log \left( {1 - \frac{1}{T}} \right)} \right\}^{ - \xi } } \right].$$
(8)

By substituting into Eq. 8, we obtain the maximum likelihood estimates of the return levels. Confidence intervals for the return level estimates are obtained by means of the delta method (Roa 1973).

The 20- and 100-year return levels for each station are shown in Table 6. It is clear that at each station, there only 1–4 observed annual maximum precipitation exceeded the 20-year return level. None of the observed annual maximum precipitation has exceeded the 100-year return level in ABT, BAT and HAM stations, while just one observed annual maximum precipitation has exceeded the 100-year return level in SEG and TAZ stations, respectively.

Table 6 Return levels for each station
Full size table

Conclusion

In the current study, the annual maximum precipitation of the five stations in the Oued El Gourzi Watershed is fitted by generalized extreme value (GEV) distribution. The effect of linear trend in time has been analyzed in this research. Stationary model (model 0) and two non-stationary models, model 1 (linear trend in location), model 2 (linear trend in both location and scale), were proposed. The different proposed models are compared using AICc and BIC criteria. The results show that the model 1 and model 2 are the most adequate models for explaining the variance in annual maximum precipitation data over the Oued El Gourzi Watershed. This case study shows that it is necessary to incorporate non-stationarity into annual maximum precipitation by linking time with the distribution parameters to improve estimations.