Introduction

The knowledge of hydrological variables is indispensable for the management of water resources. Among the hydrological variables, precipitation is one of the most important variable. For example, its scarcity affects uses such as irrigation and public supply. Already their surplus can generate floods and erosion of the soil, damaging, respectively, cities and the use of the soil. However, one of the problems presented in precipitation studies is the lack of monitoring and temporal and spatial information on precipitation. This problem greatly affects the planning and management of water resources, especially in irrigation projects, supply reservoirs, urban drainage design and flood control systems, which need knowledge of precipitation to be planned and operated efficiently, guaranteeing essential services to the population.

In order to obtain information on rainfall in a river basin, researchers have sought techniques to explore existing rainfall data in certain parts of a basin and estimate it for areas in need or lack of hydrological information. In this context, the formation of homogeneous regions of precipitation is a tool capable of providing the spatial and temporal behaviour of precipitation. The term homogeneous regions are associated with regions that have hydrological similarity (Patil and Stieglitz 2011; Wazneh et al. 2013; Swain et al. 2016).

In this context, the Fuzzy c-means method has presented good results in the formation of regional clusters, as, for example, in the studies developed by Dikbas et al. (2011). These authors compared the Fuzzy c-means and k-means clustering methods and noted that the Fuzzy c-means method was the best for homogeneous region formation. Sadri and Burn (2011) adopted the L-moment statistic and the Fuzzy c-means method for the formation of homogeneous regions of precipitation in the Canadian provinces of Alberta, Saskatchewan, and Manitoba. Satyanarayana and Srinivas (2011) were able to identify and regionalize twenty-four homogeneous precipitation clusters throughout the Chinese territory using the Fuzzy c-means method. Farsadnia et al. (2014) adopted the self-organizing feature map (SOFM) method, along with the Fuzzy c-means, K-means, and Ward methods to identify homogeneous regions of precipitation in Mazandaran Province of northern Iran. Goyal and Gupta (2014) compared the Fuzzy c-means and k-means methods in the definition of homogeneous regions of precipitation in Northeast India and concluded that the Fuzzy c-means method presented better results in the formation of regions.

Existing precipitation studies, carried out by Brazilian Agricultural Research Corporation—EMBRAPA (1994), by the National Water Agency—ANA (2009) and by Loureiro et al. (2015), which adopted geostatistical interpolation in the region, characterized the precipitation, considering only the behaviour of the historical series and identified that the total rainfall decreases in the north–south direction. However, the formation of homogeneous regions by the fuzzy group c-means taking in account the series of precipitation, geographic, and climatic characteristics of the basin, making this method complete, since the precipitation is influenced by several climatic elements, such as altitude and the geographic position, which were adopted in this study. In relation to the formation of homogeneous regions, comparing to other methods, the Fuzzy c-means is based on the concept of pertinence, identifying homogeneous regions with less subjectivity than other methods.

The Hydrographic Region of Tocantins–Araguaia—HRTA is of great importance for Brazil due the hydroelectric production. In addition to hydroelectric potential, the region has excelled in mining, agroindustry, agriculture, and livestock, and especially in irrigation projects for corn, rice, and soybeans. EMBRAPA (2014) registered 109.5 thousand hectares of irrigable areas in the region. Thus, the objective of the paper is to identify homogeneous regions of precipitation in the HRTA, using Fuzzy c-means method, showing the spatial variability of annual rainfall totals in the region. These results can be used by society towards a more sustainable use of water resources, especially for this region, which has a big demand for water resources.

Materials and methods

Study area

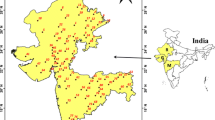
The region lies between the south parallel 0°30′ and 18°05′ and the longitude meridians 45°45′ and 56°20′. Its configuration is elongated, with a South–North direction, following the predominant direction of the main watercourses, the Tocantins and Araguaia rivers. The total drainage area of the HRTA is 918.822 km2 and covers part of the Midwest, North and North-east regions of Brazil. This region has a tropical climate, with an average annual temperature of 26 °C, and two well-defined climatic periods: rainy, from October to April, with more than 90% precipitation, with the existence of some dry days between January and February, forming the so-called summer; and dry matter, from May to September, with low relative humidity. The water balance of the region estimates that the average annual precipitation is of the order of 1.837 mm and the flow is of 13.624 m3/s and the actual evapotranspiration is 1.371 mm, which represents 75% of the precipitation, while the annual average real evapotranspiration of the country is 1.134 mm or 63% of the precipitation, and the mean coefficient of surface flow is 0.30 (National Water Agency (ANA) 2009). Figure 1 presents that HRTA is divided into three sub-basins: Alto Tocantins (ATO), Baixo Tocantins (BTO), and Araguaia (ARA). This figure also shows the use and occupation of soil, indicating strong anthropic action and the use of water resources mainly destined to hydroelectric production. Thus, the hydrographic basin is of great importance for Brazil, since its source has been exploited for the production of hydropower since the 1970s and has not yet been exhausted. Tucuruí Hydroelectric Power Plant, located in the state of Pará, is a large-scale hydroelectric power plant. In addition to hydroelectric potential, the region has excelled in mining, agroindustry, agriculture, and livestock, and especially in irrigation projects for corn, rice, and soybeans. According to the monitoring carried out by the Brazilian Agricultural Research Company—EMBRAPA, 109.5 thousand hectares of irrigable areas were registered in this region in 2014. The activities of land use and occupation are divided into urbanized areas of crops, of agroforestry systems, pastures, and agricultural establishments.

Fig. 1
figure 1

Hydrographic region of Tocantins–Araguaia (HRTA)

Full size image

Data sources

Historical series of rainfall amounts were adopted from 83 rainfall gauge station of the National Water Agency (ANA) database in HRTA (Fig. 1). The rainy seasons were chosen based on the historical series of data, opting for the stations with a larger series of data that were consistent and without observation failures. Of the 83 stations adopted, 70 had series with 30 years of data (1975–2004) and 13 stations had series ranging from 17 to 28 years (1977–2004). These series were organized in a database, which includes calculations for the average annual precipitation of each station. Information on altitude and geographic location was also extracted from the ANA database. The mean annual precipitation (MAP), altitude, latitude and longitude were used were used to apply the Fuzzy c-means method and thus identify the homogeneous regions of precipitation. Table 1 shows the rainfall gauge stations and variables used in this study.

Table 1 Rainfall gauge stations and variables used in this study
Full size table

Fuzzy c-means

In the Fuzzy c-means clustering, the partitions were generated by minimizing a function, equated by an iterative algorithm (FCM), indicating the degree of membership of an element belonging to a particular cluster. Therefore, it is a technique in which each element belongs to a cluster with a certain degree of pertinence. The technique required pre-specifications of the number of clusters to be formed. The Fuzzy c-means cluster looks for the partition that minimizes the objective function, as represented by Eq. 1.

$$J = \mathop \sum \limits_{i = l}^{n} \mathop \sum \limits_{j = l}^{p} \left( {u_{ij} } \right)^{m} d\left( {X_{i} ,C_{j} } \right)^{2} ,$$
(1)

where n is the number of data; p is the number of clusters; uij is the degree of relevance of the sample Xi to the j-th cluster; m is the fuzziness parameter; d is the Euclidean distance between Xi and Cj; Xi is the data vector, with i = 1, 2, …, n, representing a data attribute; and Cj is the centre of a fuzzy clustering. The objective function J is minimized, and the membership degrees uij are generated according to Eq. 2.

$$u_{ij} = \left[ {\mathop \sum \limits_{k = l}^{c} \left( {\frac{{d(X_{i} ,C_{j} )}}{{d\left( {X_{i} ,C_{j} } \right)}}} \right)^{{2/\left( {m - 1} \right)}} } \right]$$
(2)

where Cj can be obtained by Eq. 3.

$$C_{j} = \frac{{\mathop \sum \nolimits_{j = l}^{n} (u_{ij} )^{m} X_{i} }}{{\mathop \sum \nolimits_{j = l}^{n} (u_{ij} )^{m} }}$$
(3)

The degrees of membership uij, representing the probabilities, are generated from a uniform distribution in the interval [0,1]. The clusterings are modified at each iteration following the algorithm (Fig. 2).

Fig. 2
figure 2

Structure of the Fuzzy c-means algorithm

Full size image

The fuzziness parameter (m) is also known as the Fuzzy weight exponent and is a parameter that controls the level of diffusivity in the classification process. Thus, for m = 1, the clusters have strict limits equivalent to those of the k-means and, as the value increases, the boundaries become more diffuse. According to Cox (2005), m is usually in the range of 1.25–2.0. The cluster decision is defined by the greater degree of relevance presented for each element analysed. Thus, for a given \(X_{i}\), its greater degree of pertinence will determine to which cluster this \(X_{i}\) belongs, which clusters all the data and avoids equivocations and rigidity in the formation of the clusterings.

PBM validation index

One of the questions in a clustering analysis is the validation of the formed clusters. To achieve a good result, it is necessary to evaluate which partition is most suitable for the data and whether the partition generated by the algorithm is of good quality. To answer these questions, there are several validation indices in the literature, such as the VPC and VPE index (Bezdek 1981); the VWPE index (Windhan 1981); the VMPC index (Fukwyama and Sugeno 1989) and the PBM index (Pakhira et al. 2004).

In this study, the PBM index was used to validate the clusters and assess both the distances between the clusters formed and those between the elements and the centres of the formed clusters, which makes the validation safer. According to Pakhira et al. (2004), the PBM index serves to validate the number of clusters or subsets formed from a dataset. This index is defined as the product of three factors (Eq. 4), of which maximization ensures that the partition has a small number of compact clusters with large separations between at least two.

$${\text{PBM}} \left( k \right) = \left( { \frac{1}{k} \cdot \frac{{E_{1} }}{{E_{k} }} \cdot D_{k} } \right)^{2}$$
(4)

where k is the number of clusters.

The factor E1 (Eq. 5) is the sum of the distances of each sample to the geometric centre of all samples w0. This factor does not depend on the number of clusters.

$$E_{1 } = \mathop \sum \limits_{t - 1 \ldots n} d\left( {x\left( t \right), W_{0} } \right)$$
(5)

The factor Ek (Eq. 6) is the sum of the distances between the clusters of K clusterings and is weighted by the corresponding relevance value of each sample to the cluster.

$$E_{k} = \mathop \sum \limits_{t = 1 \ldots n} \mathop \sum \limits_{i = 1 \ldots k} ui\left( t \right)d\left( {x\left( t \right), W_{i} } \right)^{2}$$
(6)

\(D_{k}\) (Eq. 7) represents the maximum separation of each pair of clusterings.

$$D_{k} = \mathop {\hbox{max} }\limits_{i,j = 1 \ldots k} \left( {d\left( {w_{i} , w_{j} } \right)} \right)$$
(7)

The procedure to calculate the PBM index can be described as follows:

  1. 1.

    Select the maximum number of clusters M;

  2. 2.

    Calculate the factor E1;

  3. 3.

    For K = 2 to K = M, do:

    1. a.

      Run the FCM algorithm;

    2. b.

      Calculate the factors Ek and Dk;

    3. c.

      Calculate the PBM index (k).

  4. 4.

    Determine the best number of clusters K (Eq. 8).

    $$K = \hbox{max} { \arg }\left( {{\text{PBM}}\left( k \right)} \right)$$
    (8)

The PBM index is an optimization index, so to obtain the best partition, one must process the algorithm for several K values and choose the one that results in the highest index value because the higher the PBM index, the better the partition (Pakhira et al. 2004).

L-moments

The L-moments make up a system of more reliable statistical measures for describing the characteristics of probability distributions and are derived from the probability-weighted moments (PWM) as generalized by Hosking and Wallis (1993). These moments are considered measures of the position, scale and shape of the probability distributions and are similar to conventional moments, but estimated by linear combinations (Eq. 9), asymmetry, kurtosis and the coefficient of variation.

$$\beta_{r} = E\left\{ {X\left[ {Fx\left( x \right)} \right]} \right\}$$
(9)

where βr is the probability-weighted moment (PWM); E is the probability of occurrence of the variable; and Fx(x) is the cumulative distribution function of X. According to Naghettini and Pintpo (2007), the estimation of βr, from a finite sample of size n, begins with the ordering of its constituent elements in ascending order, that is, X1: n ≤ X2: n ≤ … Xn: n and the values of the observed variable. Thus, the sample L-moments are calculated (Eqs. 10–13).

$$\beta_{r} = \frac{1}{n} \mathop \sum \limits_{j = r + 1}^{n} \frac{{\left( {j - 1} \right)\left( {j - 2} \right) \ldots \left( {j - r} \right)}}{{\left( {n - 1} \right)\left( {n - 2} \right) \ldots \left( {n - r} \right)}}x_{j:n}$$
(10)
$$\beta_{0} = \frac{1}{n} \mathop \sum \limits_{j = 1}^{n} x_{j:n}$$
(11)
$$\beta_{1} = \frac{1}{n} \mathop \sum \limits_{j = 2}^{n} \frac{{\left( {j - 1} \right)}}{{\left( {n - 1} \right)}}\quad x_{j:n}$$
(12)
$$\beta_{2} = \frac{1}{n} \mathop \sum \limits_{j = 1}^{n} \frac{{\left( {j - 1} \right)\left( {j - 2} \right)}}{{\left( {n - 1} \right)\left( {n - 2} \right)}}x_{j:n}$$
(13)

where Xj represents the samples, and n is the number of samples. These estimators serve to calculate the first four moments: λ1, λ2, λ3, and λ4, which are obtained using Eqs. 14, 15, 16 and 17, respectively.

$$\lambda_{1} = \beta_{0}$$
(14)
$$\lambda_{2} = 2\beta_{1} - \beta_{0}$$
(15)
$$\lambda_{3 } = 6\beta_{2} - 6\beta_{1} + \beta_{0}$$
(16)
$$\lambda_{4 } = 20\beta_{3} - 30\beta_{2} + 12\beta_{1 } - \beta_{0}$$
(17)

Regarding shape measurements of distributions, it becomes more convenient for the L-moments to be expressed in dimensionless quantities. These quotients serve to determine the standard deviation of the homogeneous regions and are obtained using Eqs. 18–20.

$$Cv - L = \tau_{2} = \frac{{\lambda_{2} }}{{\lambda_{1} }}$$
(18)
$$\gamma - L = \tau_{3} = \frac{{\lambda_{3} }}{{\lambda_{2} }}$$
(19)
$$K - L = \tau_{4} = \frac{{\lambda_{4} }}{{\lambda_{2} }}$$
(20)

The determination of the L-moments (MML) and L-moment quotients in hydrological studies of a given region can help in the treatment of data consistency, regional analysis and the identification of homogeneous regions. The advantage of this method is that it requires less computational effort to solve systems of equations (Naghettini and Pintpo 2007). The use of this methodology allows the use of the H test, which uses the L-moment quotients to test the homogeneity of regions classified as homogeneous.

Heterogeneity Test H

The measure of heterogeneity H (Eq. 21), which is used in hydrology and meteorology, was proposed by Hosking and Wallis (1993) and aims to verify the degree of heterogeneity of a region by comparing the observed and expected variability of a homogeneous region based on L-statistics. This measure assists in determining the homogeneity of the regions formed in the cluster.

$$H = \frac{{\left( {V - \mu_{v} } \right)}}{{\sigma_{v} }}$$
(21)

where V is the sample-weighted standard deviation for CV-L, µv is the arithmetic mean of the statistics Vj obtained by simulation, and \(\sigma_{v}\) is the standard deviation between the values of the dispersion measure of the simulated samples (nsim), which are obtained using Eqs. 22, 23 and 24, respectively.

$$V = \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} n_{i} \left( {t^{i} - t^{R} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} n_{i} }}} \right]$$
(22)
$$\mu_{v} = \frac{{\mathop \sum \nolimits_{j = 1}^{{n_{\text{sim}} }} V_{j} }}{{n_{\text{sim}} }}$$
(23)
$$\sigma_{v} = \sqrt {\frac{{\mathop \sum \nolimits_{j = 1}^{{n_{\text{sim}} }} (V_{j} - \mu_{v} )^{2} }}{{N_{\text{sim}}^{ - 1} }}}$$
(24)

The determination of H starts with the calculation of the weighted standard deviation V of CV-Ls of the observed samples. Then, the simulation of the homogeneous region of precipitation is simulated from the adjusted Kappa distribution (Eq. 25), which obtains the quotients of regional L-moments. Next, the statistics Vj (j = 1, 2, …Nsim) are calculated (Eq. 23) for all homogeneous regions.

$$F\left( x \right) = \left\{ {1 - h\left[ {1 - \frac{{k\left( {x - \xi } \right)}}{\alpha }} \right]^{{\frac{1}{k}}} } \right\}^{1/h}$$
(25)

where x is the studied variable, ξ is the position parameter, α is the scale parameter, and k and h are the shape parameters. According to the test of significance, which was proposed by Hosking and Wallis (1997), if H < 1, the region is considered “acceptably homogeneous”, if 1 ≤ H < 2, the region is “possibly homogeneous,” and finally, if H ≥ 2, the region should be classified as “definitely heterogeneous”.

Results and discussion

Formation of homogeneous regions

In total, 63 clusterings were performed by varying the fuzziness parameter from 1.2 to 2.0 and the number of clusters from 2 to 15. However, it was verified that the larger the number of clusters, the smaller the value of the PBM index. In this way, tests of up to 8 clusters were performed, ensuring the objectivity of the research, since the PBM index would tend to decrease with clusters greater than 8. The choice for the best cluster was determined by the PBM index, which presented a higher index (Fig. 3) in the formation of three clusters with a fuzziness parameter equal to 1.9 (Table 2).

Fig. 3
figure 3

PBM indices of the clusters

Full size image
Table 2 Results of the application of the PBM index to the clusterings of the algorithm FCM
Full size table

One of the results from the FCM algorithm is the degree of the pertinence of the clustered elements. This degree of pertinence refers to the probability that an element belongs to a particular cluster. Thus, all of the rainfall gauge stations, which are represented by their characteristics of mean annual precipitation, altitude, and location, are presented a pertinence degree for each cluster. For example, the Acampamento IBDF Station (E8) has for Clusters 1, 2, and 3 a degree of pertinence of 0.34, 0.15, and 0.52. According to Mingoti (2005), this station has an approximate 52% probability of belonging to Cluster 3. Thus, the decision to allocate the station to a given cluster is due to its degree of pertinence (Fig. 4).

Fig. 4
figure 4

Pertinence degrees of the stations by cluster

Full size image

The clusters formed represent the homogeneous regions of precipitation. Region I is formed by 52 stations, Region II is formed by 21 stations, and Region III is formed by 10 stations according to their pertinence degrees. In the formation of the clusters by the Fuzzy c-means, the rainfall stations are clustered considering the similarity between the elements of the cluster, according to the characteristics involved in the clustering analysis, in which each cluster has its clustering centre (Fig. 5).

Fig. 5
figure 5

Clusterings according to the precipitation and altitude characteristics

Full size image

Region I is formed by the rainfall stations with a mean of 1625 mm, a minimum of 1187 mm, and a maximum of 1990 mm. These stations are concentrated in the central and south-western portion of the HRTA, specifically in the sub-basins of Alto Tocantins and Araguaia, where the Cerrado biome dominates the tropical climate with a low rainfall index. Region II is formed by stations with average annual precipitations of approximately 1700 mm, a minimum of 1349 mm and a maximum of 1989 mm. Most of the stations in this cluster are distributed in the south and south-east portions of the HRTA. The predominant biome in this region is also the Cerrado. Region III is formed by stations that present higher volumes of precipitation, with an average of 2400 mm, a minimum of 2025 mm, and a maximum of 2843 mm. The stations of this cluster are concentrated in the northern portion of the HRTA and in the region Baixo Tocantins, where the Amazonian biome predominates with a hot and humid climate and a high rainfall index (Fig. 6).

Fig. 6
figure 6

Homogeneous regions of HRTA precipitation

Full size image

Heterogeneity Test H

The calculation of the heterogeneity measure of the homogeneous regions was made by comparing the variances between the observed and simulated CV-L. In this way, the heterogeneity measure is calculated according to Eq. 21. In the verification of the Heterogeneity Test H, a value of 0.047, − 0.0049, and − 0.7874 was obtained for Region I, Region II, and Region III, respectively (Table 3), which confers acceptably homogeneous regions, since all H < 1.

Table 3 Average of L-moment quotients and the H value of the homogeneous regions
Full size table

The significance of the measure of heterogeneity can be visualized using the L-moment quotient diagrams (Fig. 7). In diagrams such as these, a possibly homogeneous region would have CV-L samples less dispersed than those obtained by simulation. In quantitative terms, this idea can be translated by the difference centred between the observed and simulated dispersions. The dispersion in the simulated regions, for the L-moment quotients, shows that there was no dispersion of the data, and, therefore, there are no stations with mean values much greater or less than the expected values. Thus, the simulated and observed dispersions are similar and form an acceptably homogeneous region.

Fig. 7
figure 7

Scatter plot of CV-L and L-Asymmetry quotients

Full size image

Conclusion

The combined use of the Fuzzy c-means method, the PBM index, and the H Heterogeneity Test was satisfactory for the formation and validation of homogeneous regions of precipitation. The satisfactory results of the application of the methodology were indicated by the formation of distinct clusters, with well-defined homogeneous regions, showing the spatial variability of annual rainfall totals in the region. In addition to contributing to the understanding of the hydrological behaviour of the region, the formation of these homogeneous regions of precipitation will aid in regionalization studies and support the management and planning of water resources in the Hydrographic Region of Tocantins–Araguaia—HRTA that is of great importance for Amazon and Brazil.