Introduction

Several models have been developed to predict the stream–aquifer interaction under varying hydrological conditions. These models have been discussed analytically and numerically with and without recharge rate by several researchers. In the past few decades, in order to augment groundwater resources, artificial recharge of unconfined aquifers is applied by means of infiltrating or recharge basins. Many researchers have studied groundwater flow in unconfined aquifers in the presence of recharge through infiltrating basins and have obtained analytical expressions for the rise and fall of groundwater mound. The linearized solutions of the Boussinesq equation have been derived by many authors. The basic assumption was groundwater flow in isotropic, homogeneous, unconfined aquifers with constant recharge from infiltrating basins which percolates vertically downwards until it approaches the water table. They considered accretion rate is small in comparison with hydraulic conductivity which is almost completely diverted in the direction of the slope of the water table and also one of the assumption is the maximum rise in the water table is small compared with the initial water table height above the base of the aquifer. An exhaustive literature is available where various authors have made their valuable contribution to discuss this phenomenon from different viewpoints.

The earliest study on the interaction of river and aquifer was developed by Theis (1941). He derived an analytical solution for estimation of the flow from a stream to an aquifer caused by pumping near the stream. Serrano and Workman (1998) presented a numerical model for modeling transient stream/aquifer interactions in an alluvial valley aquifer. The model is based on the one-dimensional Boussinesq equation for horizontal unconfined aquifer which was solved using a decomposition method. Parlange et al. (2001) developed a numerical model based on the one-dimensional Boussinesq equation for horizontal unconfined aquifer and obtained its solution by solving it using finite element program. Verhoest et al. (2002) presented a numerical model and compared the results against a transient analytical solution. The numerical scheme used the Crank–Nicholson approximation and a finite element mesh to solve the one-dimensional linearized form of Boussinesq equation. The finite element scheme employed a piecewise-linear Lagrange basis function and a piecewise-uniform weighting function. Xie and Yuan (2010) developed a statistical–dynamical scheme for water table prediction under stream–aquifer interaction in an arid region. Bansal and Das (2009) and Bansal (2014) obtained new analytical solutions of a linearized Boussinesq equation characterizing groundwater flow in a stream–unconfined aquifer. In the present paper, approximate analytical solution for interaction between stream and unconfined aquifer is obtained assuming one-dimensional horizontal groundwater flow in homogeneous and isotropic aquifer. Under the assumption of homogeneous and isotropic aquifer, the nonlinear Boussinesq equation with recharge is solved using variational homotopy perturbation method.

Mathematical formulation and approximate analytical solution

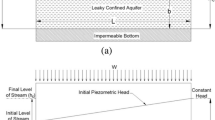
Consider an idealized cross section of the model portrayed in Fig. 1; the aquifer is in interaction with the stream having initial water level \(h_{L}\) at one termination and constant piezometric head at the other termination.

Fig. 1
figure 1

Graphic representation of an unconfined aquifer with horizontal impermeable bed

Full size image

For one-dimensional homogeneous, isotropic aquifer, equation with accretion equation is given by:

$$\frac{\partial h}{\partial t} = \frac{K}{{S_{y} }}\left[ {h\frac{\partial h}{\partial x} + \left( {\frac{\partial h}{\partial x}} \right)^{2} } \right] + \frac{R}{{S_{y} }}.$$
(1)

The specific initial and boundary conditions for an idealized cross section of a model shown in Fig. 1 are given by:

$$h\left( {x,0} \right) = h_{0} - \frac{{h_{0} - h_{L} }}{L}x,\quad 0 \le x \le L,$$
(2)
$$h\left( {0,t} \right) = h_{0} + \frac{Rt}{{S_{y} }},\quad 0 \le t \le t_{r} ,$$
(3)
$$h\left( {L,t} \right) = h_{L} + \frac{{h_{0} - h_{L} }}{{t_{r} }} + \frac{Rt}{{S_{y} }},\quad 0 \le t \le t_{r} .$$
(4)

The approximate analytical solution of Eq. (1) obtained by using variational homotopy perturbation method is shown in the subsequent section. Here, \(h_{0}\) is the piezometric head at the left boundary, \(h_{L}\) is the initial water level in the stream, t is the time, L is the length of the aquifer and \(t_{r}\) is the time in which stream water rises from \(h_{L}\) to \(h_{0}\). Here, at the right boundary x = L, time-varying boundary is considered to be increasing linearly with time. The initial condition is also assumed to be decreasing linearly with the space variable. x denotes the horizontal x axis and h(x, t) is the height of the water table above the impermeable bed of the aquifer.

Using the following non-dimensional variables,

$$X = \frac{x}{L}, T = \frac{{Kh_{ * } }}{{L^{2} S_{y} }}t,H = \frac{h}{{h_{ * } }},\quad {\text{where}}\quad h_{ * } = \mathop {\hbox{max} }\limits_{x} \left\{ {h\left( {x,0} \right)} \right\}.$$
(5)

Equation (1) and the associated initial and boundary conditions (2)–(4) are written in dimensionless form:

$$\left[ {H\frac{\partial H}{\partial X} + \left( {\frac{\partial H}{\partial X}} \right)^{2} } \right] + \beta = \frac{\partial H}{\partial T},$$
(6)

where \(\beta = \frac{{L^{2} }}{{h_{ * }^{2} K}}R\) is a dimensionless number. And \(T_{r} = \frac{{Kh_{ * } }}{{L^{2} S_{y} }}t_{r}\) is the dimensionless rising period.

$$H\left( {X,0} \right) = \frac{{h_{0} }}{{h_{ * } }} - \frac{{h_{0} - h_{L} }}{{h_{ * } }}X,\quad 0 \le X \le 1,$$
(7)
$$H\left( {0,T} \right) = \frac{{h_{0} }}{{h_{ * } }} + \beta T\quad {\text{for}}\quad 0 \le T \le T_{r} ,$$
(8)
$$H\left( {1,T} \right) = \frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T + \beta T\quad {\text{for}}\quad 0 \le T \le T_{r} .$$
(9)

The approximate analytical solution of Eq. (6) is obtained using variational homotopy perturbation method (VHPM).

Applying first variational iteration method to Eq. (6), we construct the correction functional for equation as

$$H_{n + 1} \left( {X,T} \right) = H_{n} \left( {X,T} \right) + \int\limits_{0}^{T} {\left[ {\lambda \left( \tau \right)\left( \begin{aligned} \frac{{\partial H_{n} \left( {X,T} \right)}}{\partial \tau } - \left( {\frac{{\partial \tilde{H}_{n} \left( {X,T} \right)}}{\partial X}} \right)^{2} \hfill \\ - \tilde{H}_{n} \left( {X,T} \right)\,\left( {\frac{{\partial^{2} \tilde{H}_{n} \left( {X,T} \right)}}{{\partial X^{2} }}} \right) - \beta \hfill \\ \end{aligned} \right)} \right]} {\text{d}}\tau ,$$
(10)

where \(\lambda (\tau )\) is a Lagrange multiplier (He 2007) which can be readily identified as  = − 1 stated above. Substituting this value of the Lagrange’s multiplier into functional (10) gives the iteration formula

$$H_{n + 1} \left( {X,T} \right) = H_{n} \left( {X,T} \right) - \int\limits_{0}^{T} {\left[ {\left( {\frac{{\partial H_{n} }}{\partial \tau } - \left( {\frac{{\partial H_{n} }}{\partial X}} \right)^{2} - H_{n} \,\left( {\frac{{\partial^{2} H_{n} }}{{\partial X^{2} }}} \right) - \beta } \right)} \right]} {\text{d}}\tau .$$
(11)

Following VHPM (Daga and Pradhan 2014a, b; Desai et al. 2015) as stated above, we have

$$\sum\limits_{i = 0}^{\infty } {p^{i} h_{i} } = H_{0} \left( {X,T} \right) - p\int\limits_{0}^{T} {\left[ {\left( { - \left( {\frac{{\partial \sum\limits_{i = 0}^{\infty } {p^{i} h_{i} } }}{\partial X}} \right)^{2} - \sum\limits_{i = 0}^{\infty } {p^{i} h_{i} } \left( {\frac{{\partial^{2} \sum\limits_{i = 0}^{\infty } {p^{i} h_{i} } }}{{\partial X^{2} }}} \right)} \right)} \right]} {\text{d}}\tau + \int\limits_{0}^{T} {\beta {\text{d}}\tau } .$$
(12)

Comparing the coefficient of like powers of p, we obtain the following components

$$h_{0} (X,T) = aX^{2} + bX + c + \beta T,$$
(13)
$$h_{1} (X,T) = T(b^{2} + 6abX + a(2c + 6aX^{2} + T\beta )),$$
(14)
$$h_{2} (X,T) = \frac{1}{3}aT^{2} (21b^{2} + 108abX + 2a(12c + 54aX^{2} + 7T\beta )),$$
(15)
$$h_{3} (X,T) = \frac{2}{3}a^{2} T^{3} (67b^{2} + 324abX + a(56c + 324aX^{2} + 35T\beta )),$$
(16)
$$h_{4} (X,T) = \frac{4}{3}a^{3} T^{4} (208b^{2} + 972abX + a(140c + 972aX^{2} + 91T\beta )).$$
(17)

Proceeding in similar manner, we can obtain further approximations.

Thus,

$$\begin{aligned} H\left( {X,T} \right) & = h_{0} \left( {X,T} \right) + h_{1} \left( {X,T} \right) + h_{2} \left( {X,T} \right) + h_{3} \left( {X,T} \right) + h_{4} \left( {X,T} \right) \\ & = aX^{2} + bX + c + \beta T + T(b^{2} + 6abX + a(2c + 6aX^{2} + T\beta )) \\ & \quad + \frac{1}{3}aT^{2} (21b^{2} + 108abX + 2a(12c + 54aX^{2} + 7T\beta )) \\ & \quad + \frac{2}{3}a^{2} T^{3} (67b^{2} + 324abX + a(56c + 324aX^{2} + 35T\beta )) \\ & \quad + \frac{4}{3}a^{3} T^{4} (208b^{2} + 972abX + a(140c + 972aX^{2} + 91T\beta )). \\ \end{aligned}$$
(18)

Equation (18) is the approximate analytical solution for horizontal unconfined aquifer with infiltration.

The approximate analytical solution is numerically validated and shown in subsequent section.

Numerical Solution (B-spline finite element method)

To solve (6) together with initial condition (7) and boundary conditions (8)–(9) dividing the time domain \(\left[ {0,T_{r} } \right]\) with the equal length \(\Delta T = \frac{{T_{r} }}{q}\) into q subintervals (where \(T_{r}\) is the total time and q is a positive integer) and replacing the time derivative of the difference quotient \(\frac{{H_{j} \left( X \right) - H_{j - 1} \left( X \right)}}{\Delta T}\) at each \(T_{j} = j\Delta T\), j = 1,2,…,q (where \(H_{j} \left( X \right)\) is the approximation of H for \(T = T_{j}\)), the partial differential Eq. (6) is converted into the following ordinary differential equation:

$$\frac{1}{\Delta T}\left( {H_{j} \left( X \right) - H_{j - 1} \left( X \right)} \right) - \left( {H_{j} \left( X \right)\,H_{j}^{'} \left( X \right)} \right)^{'} - \beta = 0,$$
(19)

with boundary conditions where j =1, 2, …, q.

Now weighted integral statement of Eq. (19) is

$$\int\limits_{0}^{1} {w\left( X \right)\left( {\frac{1}{\Delta T}\left( {H_{j} \left( X \right) - H_{j - 1} \left( X \right)} \right) - \left( {H_{j} \left( X \right)\,H_{j}^{'} \left( X \right)} \right)^{'} - \beta } \right)} {\text{d}}X = 0.$$
(20)

Integration by parts leads to the following equation:

$$\frac{1}{\Delta T}\int\limits_{0}^{1} {w\left( X \right)H_{j} \left( X \right){\text{d}}X} + \int\limits_{0}^{1} {w^{'} \left( X \right)H_{j} \left( X \right)H_{j}^{'} \left( X \right){\text{d}}X} = \left[ {w\left( X \right)H_{j} \left( X \right)\,H_{j}^{'} \left( X \right)} \right]_{0}^{1} + \frac{1}{\Delta T}\int\limits_{0}^{1} {w\left( X \right)H_{j - 1} \left( X \right){\text{d}}X} + \beta \int\limits_{0}^{1} {w\left( X \right){\text{d}}X} .$$
(21)

The interval [0, 1] is divided into N elements with equal length \(\Delta X = p\) by the knots \(X_{i}\) such that \(0 = X_{0} < X_{1} < X_{2} < \cdots < X_{N} = 1.\) The set \(\left\{ {\phi_{i} } \right\}_{i = - 1}^{N}\) constitutes a basis for the functions defined on [0, 1]. Quadratic B-splines (Chapani et al. 2015) are defined by

$$\phi_{i} \left( X \right) = \frac{1}{{p^{2} }}\left\{ {\begin{array}{*{20}l} {\left( {X_{i + 2} - X} \right)^{2} - 3\left( {X_{i + 1} - X} \right)^{2} + 3\left( {X_{i} - X} \right)^{2} ,} \hfill & {[X_{i - 1} ,X_{i} ],} \hfill \\ {\left( {X_{i + 2} - X} \right)^{2} - 3\left( {X_{i + 1} - X} \right)^{2} ,} \hfill & {[X_{i} ,X_{i + 1} ],} \hfill \\ {\left( {X_{i + 2} - X} \right)^{2} ,} \hfill & {[X_{i + 1} ,X_{i + 2} ],} \hfill \\ {0,} \hfill & {{\text{otherwise}},} \hfill \\ \end{array} } \right.$$
(22)

where \(p = X_{i + 1} - X_{i}\), i =−1, 0, 1,…, N.

From the definitions of quadratic B-splines, the values of \(\phi_{i} \left( X \right)\) and its first derivative \(\phi_{i}^{'} \left( X \right)\) at the knots are obtained.

The approximate solution \(H_{j}^{N} \left( X \right)\) of the function \(H_{j} \left( X \right)\) over the space domain [0,1] can be written in terms of \(\left\{ {\phi_{i} } \right\}_{i = - 1}^{N}\) as

$$H_{j}^{N} \left( X \right) = \sum\limits_{n = - 1}^{N} {\delta_{n}^{j} \phi_{n} \left( X \right),}$$
(23)

where the unknowns parameters \(\delta_{i}^{j}\) are to be determined.

By the definition of quadratic B-splines, the nodal values \(H_{j,i}\) and \(H_{j,i}^{'}\) at the knot \(X_{i}\) can be expressed in terms of \(\delta_{i}^{j}\) as

$$\begin{aligned} & H_{j,i} = H_{j} \left( {X_{i} } \right) = \delta_{i - 1}^{j} + \delta_{i}^{j} , \\ & H_{j,i}^{'} = H_{j}^{'} \left( {X_{i} } \right) = \frac{2}{h}\left( {\delta_{i}^{j} - \delta_{i - 1}^{j} } \right). \\ \end{aligned}$$
(24)

Applying boundary conditions to Eq. (24), we get

$$\begin{aligned} & \delta_{ - 1}^{j} = 1 - \delta_{0}^{j} , \\ & \delta_{N}^{j} = \frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T_{j} \, - \delta_{N - 1}^{j} . \\ \end{aligned}$$
(25)

Using these relations in Eq. (25), we have

$$H_{j}^{N} \left( X \right) = v_{j} \left( X \right) + \sum\limits_{n = 0}^{N - 1} {\delta_{n}^{j} B_{n} \left( X \right)} ,$$
(26)

where

$$v_{j} \left( X \right) = \phi_{ - 1} \left( X \right) + \left( {\frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T_{j} } \right)\phi_{N} \left( X \right)$$
(27)

and

$$\begin{aligned} & B_{0} \left( X \right) = \phi_{0} \left( X \right) - \phi_{ - 1} \left( X \right),\; \\ & B_{i} \left( X \right) = \phi_{i} \left( X \right)\;\left( {i = 1,2, \ldots N - 2} \right), \\ & B_{N - 1} \;\left( X \right) = \;\phi_{N - 1} \left( X \right) - \phi_{N} \left( X \right). \\ \end{aligned}$$
(28)

The new set of basis functions \(B_{i} \left( X \right),i = 0,1,2, \ldots ,N - 1\) given in Eq. (28) vanishes at the boundary points and \(v_{j} \left( X \right)\) given in Eq. (27) satisfies boundary conditions.

Substituting the approximate solution from Eq. (27) into the Eq. (20), we get

$$\frac{1}{\Delta T}\sum\limits_{n = 0}^{N - 1} {\left( {\int\limits_{0}^{1} {B_{i} B_{n} {\text{d}}X} } \right)} \delta_{n}^{j} + \frac{1}{\Delta T}\int\limits_{0}^{1} {v_{j} B_{i} {\text{d}}X} + \int\limits_{0}^{1} {B_{i}^{'} v_{j} v_{j}^{'} {\text{d}}X} + \sum\limits_{n = 0}^{N - 1} {\left( {\int\limits_{0}^{1} {B_{i}^{'} \left( {v_{j} B_{n}^{'} + v_{j}^{'} B_{n} } \right){\text{d}}X} } \right)} \delta_{n}^{j} + \sum\limits_{n,m = 0}^{N - 1} {\left( {\int\limits_{0}^{1} {B_{i}^{'} B_{m}^{'} B_{n} {\text{d}}X} } \right)\delta_{m}^{j} \delta_{n}^{j} } = \frac{1}{\Delta T}\int\limits_{0}^{1} {B_{i} H_{j - 1} {\text{d}}X} + \beta \int\limits_{0}^{1} {B_{i} {\text{d}}X} ,$$
(29)

where \(i = 0,1,2, \ldots ,N - 1,j = 1,2, \ldots ,q\).

On rearranging the terms, Eq. (29) can be written as

$$\frac{1}{\Delta T}\sum\limits_{n = 0}^{N - 1} {\left( {\int\limits_{0}^{1} {B_{i} B_{n} {\text{d}}X} } \right)} \delta_{n}^{j} + \sum\limits_{n = 0}^{N - 1} {\left( {\int\limits_{0}^{1} {B_{i}^{'} \left( {v_{j} B_{n}^{'} + v_{j}^{'} B_{n} } \right){\text{d}}X} } \right)} \delta_{n}^{j} + \sum\limits_{n,m = 0}^{N - 1} {\left( {\int\limits_{0}^{1} {B_{i}^{'} B_{m}^{'} B_{n} {\text{d}}X} } \right)\delta_{m}^{j} \delta_{n}^{j} } = \frac{1}{\Delta T}\int\limits_{0}^{1} {B_{i} H_{j - 1} {\text{d}}X} - \frac{1}{\Delta T}\int\limits_{0}^{1} {v_{j} B_{i} {\text{d}}X} - \int\limits_{0}^{1} {B_{i}^{'} v_{j} v_{j}^{'} {\text{d}}X} + \beta \int\limits_{0}^{1} {B_{i} {\text{d}}X} .$$
(30)

In matrix form, it can be written as

$$\frac{1}{\Delta T}A\delta^{j} + B^{j} \delta^{j} + C\left( {\delta^{j} } \right)\delta^{j} = \frac{1}{\Delta T}D^{j - 1} - \frac{1}{\Delta T}E^{j} - F^{j} + \beta RG,$$
(31)

where \(\delta^{j} = \left( {\delta_{0}^{j} ,\delta_{1}^{j} , \ldots ,\delta_{N - 1}^{j} } \right)^{T} ,j = 1,2, \ldots ,q.\)

$$\begin{aligned} & A = \frac{p}{30}\left[ {\begin{array}{*{20}c}{40} & {25} & 1 & {} & {} & {} & {} & {} & {} \\ {25} & {66} & {26}& 1 & {} & {} & {} & {} & {} \\ 1 & {26} & {66} & {26} & 1 & {} & {}& {} & {} \\ {} & . & . & . & . & {} & {} & {} & {} \\ {} & {} & . &. & . & . & {} & {} & {} \\ {} & {} & {} & . & . & . & . & {} & {}\\ {} & {} & {} & {} & 1 & {26} & {66} & {26} & 1 \\ {} & {} & {} &{} & {} & 1 & {26} & {66} & {25} \\ {} & {} & {} & {} & {} & {} & 1& {25} & {40} \\ \end{array} } \right], \\ & B^{j} =\frac{1}{15p}\left[ {\begin{array}{*{20}r} \hfill {21} & \hfill 3 &\hfill {} & \hfill {} & \hfill {} & \hfill {} \\ \hfill { - 7} &\hfill { - 1} & \hfill {} & \hfill {} & \hfill {} & \hfill {} \\\hfill {} & \hfill {} & \hfill {} & \hfill {} & \hfill {} & \hfill{} \\ \hfill {} & \hfill {} & \hfill {} & \hfill {} & \hfill {} &\hfill {} \\ \hfill {} & \hfill {} & \hfill {} & \hfill {} & \hfill{ - \left( {\frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L}}}{{h_{ * } T_{r} }}T_{j} } \right)\,} & \hfill { - 7\left({\frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L} }}{{h_{ * }T_{r} }}T_{j} } \right)} \\ \hfill {} & \hfill {} & \hfill {} &\hfill {} & \hfill {3\left( {\frac{{h_{L} }}{{h_{ * } }} +\frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T_{j} } \right)} & \hfill{21\left( {\frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L}}}{{h_{ * } T_{r} }}T_{j} } \right)} \\ \end{array} } \right], \\ &E^{j} = \frac{p}{30}\left[ {\begin{array}{*{20}r} \hfill 7 \\ \hfill1 \\ \hfill {} \\ \hfill {} \\ \hfill {\frac{{h_{L} }}{{h_{ * } }} +\frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T_{j} } \\ \hfill {7\left({\frac{{h_{L} }}{{h_{ * } }} + \frac{{h_{0} - h_{L} }}{{h_{ * }T_{r} }}T_{j} \,} \right)} \\ \end{array} } \right],\quad F^{j} =\frac{1}{5p}\left[ {\begin{array}{*{20}r} \hfill { - 7} \\ \hfill {- 1} \\ \hfill {} \\ \hfill {} \\ \hfill { - \left( {\frac{{h_{L}}}{{h_{ * } }} + \frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T_{j} }\right)^{2} } \\ \hfill { - 7\left( {\frac{{h_{L} }}{{h_{ * } }} +\frac{{h_{0} - h_{L} }}{{h_{ * } T_{r} }}T_{j} } \right)^{2} } \\\end{array} } \right],\\&\quad G = \frac{2p}{3}\left[{\begin{array}{*{20}r} \hfill 2 \\ \hfill 3 \\ \hfill . \\ \hfill .\\ \hfill 3 \\ \hfill 2 \\ \end{array} } \right], \quad D^{j - 1} =A\delta^{j - 1} + E^{j - 1} \quad {\text{for}}\quad j \ge 2, \\ &C\left( {\delta^{j} } \right) = \left( {\frac{1}{15p}} \right)\left(\left\{ { - 3,1,2,0,0} \right\}\delta^{j} ,\left\{ { - 14, -21,34,1,0} \right\}\delta^{j} \right. ,\\&\quad \left.\left\{ { - 3, - 21,48, - 21, - 3} \right\} \delta^{j}, {\left\{ {0,1,34, - 21, - 14} \right\}\delta^{j} ,\left\{{0,0,2,1, - 3} \right\}\delta^{j} } \right), \\ \end{aligned}$$

where \(\delta^{j}\) takes the values \(\delta_{i - 2}^{j} ,\delta_{i - 1}^{j} ,\delta_{i}^{j} ,\delta_{i + 1}^{j} ,\delta_{i + 2}^{j} .\)

Equation (31) represents system of nonlinear algebraic equations consisting N unknowns and N equations. Equation (31) is solved for N = 40, \(\Delta t = 0.0001\) using Newton–Raphson method. The numerical results are obtained.

Results and discussion

Approximate analytical solution is obtained for stream–aquifer interaction with recharge for unconfined horizontal aquifer. The approximate analytical solution holds for \(0 \le T \le 0.5\) where the dimensionless rising period \(T_{r}\) = 0.5. For K = 0.001 m/s, \(S_{y}\) = 0.34, L = 100 m and \(t_{r}\) = 4 days. The boundary conditions in the present case are time varying due to the effect of recharge. Although the discussion in the present case is for small values of recharge rate, the obtained numerical results behave physically well. The corresponding graphical representation determining this fact is shown in Fig. 2. The sensitivity of these parameters is studied by considering various values of K keeping \(S_{y}\) fixed and various values of \(S_{y}\) keeping K fixed. The effect of K keeping \(S_{y}\) fixed is studied by finding the numerical values of the height of the water table which are shown in Fig. 3. It is found that on increasing the value of K keeping \(S_{y}\) fixed the height of water table increases. Similar effect of \(S_{y}\) keeping K fixed is observed finding the numerical values shown in Fig. 4. With the increase in the values of \(S_{y}\), the height of water table decreases. The numerical result of Eq. (31) is compared with approximate analytical solution (18), which is shown in Fig. 5. It is observed that the numerical values obtained by quadratic B-spline finite element method match well with the approximate analytical solution obtained by VHPM. Hence, the obtained approximate analytical solution is numerically validated. Thus, the physical fact of the soil parameters is also preserved in the present case. The numerical values are also calculated for different values of constant recharge rate R. Its graphical representation is shown in Fig. 6. Here, the values of R are taken small, since \(0 < \beta \le 0.1\) the numerical results behave well with the physical phenomena of the problem. Hence, it is concluded that the obtained approximate analytical solutions for the stream–aquifer interaction problem with recharge are in accordance with the physical phenomena. Thus, the applied variational homotopy perturbation method is efficient and reliable.

Fig. 2
figure 2

Water table profiles in unconfined aquifer with horizontal impermeable bed with recharge

Full size image
Fig. 3
figure 3

Effect of hydraulic conductivity (K) in a horizontal aquifer with recharge

Full size image
Fig. 4
figure 4

Effect of specific yield (\(S_{y}\)) in a horizontal aquifer with recharge

Full size image
Fig. 5
figure 5

Comparison of water table profiles in unconfined aquifer with horizontal impermeable bed without recharge

Full size image
Fig. 6
figure 6

Water table profiles for effect of recharge rate (R mm/h)

Full size image

Conclusion

The nonlinear Boussinesq equation signifying stream–aquifer interaction problem with recharge in horizontal unconfined aquifer is analytically discussed, and its solution is obtained using variational homotopy perturbation method. It is found that the numerical results behave well with the physical phenomena of the problem. Hence, the obtained approximate analytical solutions are found to be realistic. It is concluded that the present analytical method is reliable and can be applicable to other nonlinear equations.