Performance of a system of reservoirs on futuristic front

Abstract

Application of simulation model HEC-5 to analyze the performance of the DVC Reservoir System (a multipurpose system with a network of five reservoirs and one barrage) on the river Damodar in Eastern India in meeting projected future demand as well as controlling flood for synthetically generated future scenario is addressed here with a view to develop an appropriate strategy for its operation. Thomas-Fiering model (based on Markov autoregressive model) has been adopted for generation of synthetic scenario (monthly streamflow series) and subsequently downscaling of modeled monthly streamflow to daily values was carried out. The performance of the system (analysed on seasonal basis) in terms of ‘Performance Indices’ (viz., both quantity based reliability and time based reliability, mean daily deficit, average failure period, resilience and maximum vulnerability indices) for the projected scenario with enhanced demand turned out to be poor compared to that for historical scenario. However, judicious adoption of resource enhancement (marginal reallocation of reservoir storage capacity) and demand management strategy (curtailment of projected high water requirements and trading off between demands) was found to be a viable option for improvement of the performance of the reservoir system appreciably [improvement being (1–51 %), (2–35 %), (16–96 %), (25–50 %), (8–36 %) and (12–30 %) for the indices viz., quantity based reliability, time based reliability, mean daily deficit, average failure period, resilience and maximum vulnerability, respectively] compared to that with normal storage and projected demand. Again, 100 % reliability for flood control for current as well as future synthetically generated scenarios was noted. The results from the study would assist concerned authority in successful operation of reservoirs in the context of growing demand and dwindling resource.

Introduction

Large man-made reservoirs are constructed and operated for multiple purposes viz., meeting municipal, industrial, agricultural water demand, power generation, recreational use of the reservoir pool, maintenance of water quality downstream of the reservoir and also for flood control. These needs impose constraints on the storage and release of water from the reservoir and the conditions have further been aggravating in the context of rising demand and increasing cases of pollution. With growing environmental concern and decreasing public support for new reservoirs, development and use of computer models for analysis of operation of existing system for improvement of its performance rather than designing new projects, is receiving considerable attention. In this background, this paper describes an application of simulation model (HEC-5 1998) to analyze the performance of the DVC reservoir system on the river Damodar in eastern India in meeting demands as well as controlling flood for synthetically generated scenario (with projected future demand) and to explore an appropriate policy for improvement of its performance in the future scenario.

The study has been carried out into four stages. Firstly, simulation run for the operation of the DVC reservoir system was carried out for historical scenario (with daily input data for historical years) with help of HEC-5 simulation model and performance of the system was assessed in terms of seven ‘Performance Indices’ (Quantity based and Time based reliabilities, Mean daily deficit, Average failure period, Resilience, Maximum Vulnerability and Flood Control Index). In the second stage, synthetic scenario was generated through modeling of monthly stream flow for future time frame using the Thomas-Fiering model (based on Markov autoregressive model) (Patra 2001). Subsequently, daily flow data was generated from monthly flow data using temporal downscaling technique (Wood et al 2004) for use as input to the HEC-5 model. In the third stage, operational policies for future scenario were enumerated for various combinations of resource enhancement and demand management strategies and simulation run for the operation of the DVC reservoir system was carried out for synthetically generated scenario (with projected future demand) with help of HEC-5 simulation model for aforementioned policies and performance of the system was assessed. Finally an appropriate policy for improvement of system performance in the future scenario (with projected future demand) was delineated by carrying out comparative analysis of aforementioned performance indices.

It may be noted that to the best of our knowledge, no work related to delineation of policy for improvement of performance for the DVC reservoir system in futuristic front has been carried out earlier.

Reservoir systems are generally analyzed by using mathematical models which are categorized as simulation and optimization. Optimization models are used to determine the “best” way to meet some objective. Simulation models are used to predict system performance for a specified set of input data. A number of simulation model runs are normally carried out to evaluate the performance of the system under a variety of conditions and this may be used to determine optimum solution (Viessman and Welty 1985). The USACE Hydrologic Engineering Center (1991) presents a comprehensive review of reservoir system modeling (including HEC-5) and analysis approaches.

Needham et al. (2000) carried out flood control study in the Iowa and Des Moines rivers in USA and concluded that optimization methods when used in conjunction with simulation model yield the best results. Chang et al. (2010) proposed a model which involves integration of operating rules, the stepwise optimal water allocation model and the convex hull multiobjective generic algorithm to solve multiobjective regional water allocation planning problem for the Kao Pin River and Tseng-Wen river basin in Taiwan. Rani and Moreira (2010) presented a survey of simulation and optimization modeling approaches used in reservoir systems operation problems and concluded that the two approaches when combined give the best results. Wurbs (2011) presented an excellent review of capabilities of computer models (developed in USA) for simulating control, allocation and management of river basins and these models would be of assistance for practicing engineers in management of various types of river/reservoir system. Fayaed et al. (2012) presented an overview of simulation and optimization modeling methods utilized in resolving critical issues with regard to reservoir systems and stated that reservoir simulation constitutes one of the most important steps to be considered. Ashofteh et al. (2013) addressed the impact of climate change on the volume of inflow to a reservoir and the volume of downstream water demand by considering three climate change scenarios for 2026–2039 under A2 emission scenario in an East Azerbaijan river basin and using both simulation and optimization models of reservoir operation. Ghimire and Reddy (2014) presented optimization and uncertainty analysis of operation policies for maximizing total hydropower production, subject to satisfying the requirements for irrigation as well as maintaining the flood control restrictions for multipurpose Hirakud reservoir system in State of Orissa in India. Jahanpour et al. (2014) developed a web-based application for reservoir operation using an optimization approach for the Ekbatan Dam located in the upstream of Yalfan River, Iran. Fang et al. (2014) developed a simulation–optimization model using the improved particle swarm optimization (IPSO) algorithm for a multi-reservoir water supply system (including a water transfer-supply project) located in Liaoning Province, China. Prakash et al. (2014) proposed a multi-objective simulation–optimization (S–O) framework with non-dominated sorting genetic algorithm-II (NSGA-II) as the solution technique for flood mitigation in a river-reservoir system with multiple reservoirs and control points for obtaining compromising solutions for the flood mitigation. Liu et al. (2015) proposed a simulation-based optimization model to develop seasonal’ Flood Limited Water Level Scheme’ involving trade offs among flood control, hydropower generation and navigation and enhancement of the economic benefits without increasing the flood risk for China’s Three Gorges Reservoir.

It may be noted that HEC-5 simulation model has been pointed out as being a well documented model and being used in a relatively large number of studies, including studies of storage reallocations and other operational modifications at existing reservoirs as well as feasibility studies for proposed new projects and for real-time operation [USACE Hydrologic Engineering Center (1991)]. Regan (2011) reported the use of HEC-5 simulation model by the Environmental Protection Division (EPD), Georgia-Watershed Protection Branch, USA. Awadallah and Awadallah (2014) determined a suitable and feasible water allocation/pumping policy as a “trade-off” between minimizing the water deficiency and the cost of pumping using HEC-5 simulation model for reservoir operation for a system of three dams, two pumping stations and two diversion structures located in the Upper-Chéliff (Algeria) in Northwest Africa.

Study area

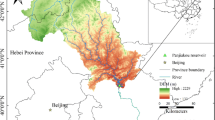
The Damodar and its three tributaries—the Bokaro, the Konar and the Barakar—form one important tributary of the Bhagirathi-Hugli (a distributory of the Ganga) in its lower reaches.

Damodar river basin is the most important sub-basin of the GBM basin since India’s first river development project, Damodar Valley Corporation (DVC) came into being on the river Damodar. The four main multipurpose dams located at Tilaiya (on Barakar river), Konar (on Konar river), Maithon (on Barakar river and downstream of Tilaiya dam) and Panchet (on Damodar river main stream) and a barrage at Durgapur (on Damodar river main stream and downstream of the confluence of the Barakar river with the Damodar river) (Figs. 1, 2; Table 1) were commissioned during 1953–1959. In addition, a single purpose reservoir on the main stream of the Damodar at Tenughat and upstream of Panchet dam was constructed later in 1978.

Fig. 1

A topographic view of DVC system

Fig. 2

Schematic Layout Plan for the DVC system

Table 1 Salient features of DVC reservoir system

Moderation of flood in the lower valley (below Durgapur Barrage) of the river Damodar, extension of irrigation facilities, catering municipal and industrial need, generation of hydropower and maintaining water quality, in an integrated manner are the authorized purposes of the DVC reservoir system.The industrial water demand is relatively more (by 27 %) in the upper reaches of the river valley up to the Durgapur Barrage and are met by releases from the five reservoirs. The irrigation requirements are concentrated mainly in the lower valley and is taken care of by combined releases of Maithon and Panchet reservoirs.

Data acquisition

Daily reservoir operation data for historical years spanning over 1996–2013 (which includes flow data, reservoir release), reservoir characteristic curves (elevation-storage, elevation-area and elevation-maximum outflow capacity curves based on capacity survey carried out during 2011), reservoir Guide curves for reservoir operation, maximum channel capacity, Muskingum channel routing parameters for river reaches, water demand (Table 2) at various reservoirs and barrage were collected from DVC Authority. Tables of elevation-storage-area-maximum outflow capacity were prepared from the characteristic curves for use in the simulation model. The routing coefficients were estimated directly from Muskingum model parameters. Daily gridded (0.5° × 0.5°) rainfall and daily gridded (1° × 1°) temperature data for the basins were collected from National Climatic Centre, India Meteorological Dept, Pune and other daily meteorological data such as monthly relative humidity, wind speed for the study period has been collected from the Water Resources Information System of India website for estimation of monthly average net evaporation (reflecting the reservoir gains from precipitation directly on the surface as well as the evaporation loss from the surface). Local inflows for downstream reservoirs (viz., Maithon and Panchet) and Durgapur Barrage were computed from information on routed release at concerned reservoirs from upstream reservoir and recorded inflow therein. Future water demand [50 % of the demand as projected for 2025 by WAPCOS (2010)] was rearranged to estimate pertinent water requirement from reservoirs and barrage (Table 2) for immediate near future. Municipal water demand was estimated in the aforementioned study (WAPCOS 2010) by considering growth rate of population during 1971, 1981, 1991 and 2001 in the basin. Industrial and irrigation water demands were projected in the same study (WAPCOS 2010) for future years by incorporating estimated water demands for current and proposed industrial and irrigation projects.

Table 2 Historical and Projected water demand in MCM for reservoirs and barrage

Methodology

A flow chart showing the methods used, inputs data handled and outputs obtained has been shown in Fig. 3.

Fig. 3

Flow chart of the simulation of operation of DVC reservoir system

HEC-5 model

Computer program HEC-5 is designed to perform sequential reservoir operation based on specified demands and constraints for conservation purposes and also for controlling flood for a system of reservoirs (in both parallel and series form and defined by routing reaches and specified downstream locations) for short-interval floods, for long duration non-flood periods, or for combinations of the two. Physical reservoir constraints are the available storage for flood control and conservation purposes and maximum outlet capacity. Operational constraints include maximum non-damaging flows and reservoir release, rate-of-change (based on the downstream channel’s ability to accept decreasing amounts of water without bank sloughing), reservoir Guide curves for reservoir operation. Additionally, the reservoir release may also be constrained by foresight (consideration of future flows when making release determinations). Demands can be specified at the reservoir and at downstream locations (HEC-5 1998).

The reservoir simulation attempts to meet the specified flow and diversion demands by releasing supplemental water whenever the local flow is not sufficient to supply the demands. Releases are made when the reservoir storage is greater than the top of inactive storage. No releases are made when the reservoir is below top of inactive pool. Water is stored in flood control zone when it cannot be safely passed through the downstream channel system. When the top of flood pool is exceeded, all excess flood water is released. After flooding recedes, the program will empty the flood volume in storage as quickly as possible. The simulation process determines the reservoir release at each time step and the resulting downstream flows (considering reservoir storage balance equation and linear channel routing e.g. Muskingum routing) while keeping the system in balance.

The release from the reservoir j in time period i is based on continuity equation:

$$S_{i,j} \; = \;\left[ {S_{i - 1,j} \; + \;\sum\limits_{k = 1}^{N} {\sum\limits_{t = 1}^{i} {c_{t,k} f_{t,k} \Delta t + I_{i,j} \Delta t} } } \right]\; - \;\left[ {f_{i,j} \Delta t} \right]\; - \;({\text{EVP}})_{i,j}$$

(1)

where S _i−1,j and S _i,j  = storage at the beginning and end of period i, respectively; f _i,j = total release in period i; N = set of all control points upstream of j from which flow is routed to j, f _t,k  = flow at control point k in period t; c _t,k  = linear coefficient to route period t flow from control point k to control point j for period i, I _i,j  = local inflow to the reservoir and (EVP) _i,j is the net evaporation loss during time period i for the reservoir j.

The continuity equation for each control point (excluding reservoir) is given by:

$$f_{i,j} \; = \;I_{i,j} \; + \;\sum\limits_{k = 1}^{N} {\sum\limits_{t = 1}^{i} {c_{t,k} f_{t,k} } }$$

(2)

where f _i,j  = control-point flow during period j; and I _i,j  = local inflow during period j.

The reservoir operation schedule (with Guide Curve and integrated approach as adopted by DVC Authority) was used for simulating the operation of system of reservoirs in integrated manner, starting from 1st June (beginning of water year in India). The integrated approach involves consideration of the operation of the Tilaiya reservoir in tandem with the Maithon reservoir, the operation of the Konar and Tenughat reservoirs in tandem with the Panchet reservoir and combined operation of Maithon and Panchet reservoirs for the Durgapur Barrage for conservation as well as flood management purposes. The operation schedule invokes attempt to maintain conservation storages of the reservoirs full (throughout the month of October) so as to ensure conservation requirement up to the end of summer (or up to the onset of monsoon i.e. the first week of June) along with some carry-over storage if onset of monsoon is delayed.

Thomas and Fiering model based on Markov model (based on autocorrelation of monthly flows) (Patra 2001) has been employed for generating monthly inflow series using historical monthly inflow data.

The model uses the following recursion equation:

$$q_{j} \; = \;\overline{{q_{j} }} \; + \;b_{j} (q_{j - 1} \; - \;\overline{{q_{j - 1} )}} \; + \;t_{j} S_{j} (1\; - \,r_{j}^{2} )^{1/2}$$

(3)

where q _j and q _j−1 are the discharge volumes during jth and (j − 1)th months respectively, $\overline{q}$ _j and $\overline{q}$ _j−1 are the mean monthly discharge volumes during jth and (j − 1)th months, respectively. S _j is the standard deviation for jth month, r _j is the correlation coefficient between the jth and (j − 1)th month, t _j is the random independent variate with zero mean and unit variance.

$$b_{j} \; = \;r_{j} \left( {\frac{{S_{j} }}{{S_{j - 1} }}} \right)$$

(4)

Testing for statistical similarity of the generated flow record with the historical record involves the comparison of the mean and standard deviation of the computed streamflow series and the historical streamflow series and the same has been carried out. The temporal downscaling technique as described by Wood et al. (2004) has been used to downscale the modeled streamflow data from monthly to daily values.

Operational policies

Operational policies for future scenario were framed for various combinations of resource enhancement and demand management strategies. Resource enhancement strategy through reallocation of reservoir storage capacity encompasses increasing the conservation storage volume at the expenses of flood control storage volume for reservoirs. Again relatively small storage reallocation seems to be viable keeping in view the uncertainty in occurrence of extreme rainfall events and risk associated with loss in flood control storage capacity, particularly, in case of extreme flood event. Analysis of historical record revealed occasional spells of moderately high inflow to Maithon and Panchet reservoirs to occur every year during non-monsoon months—the occurrence was found to be higher for Panchet reservoir (located on the main stream of Damodar river system) than for Maithon reservoir. Hence, an increase in storage capacity of the reservoirs (by reallocating 15 % of flood storage of Maithon reservoir and 20 % of flood storage of Panchet reservoir (flood storage capacity of Panchet reservoir being larger than that of Maithon reservoir) to corresponding conservation storages during season-3 and season-4) may be explored as a measure to improve the performance.

An analysis for seasonal inflow and seasonal demand (during season-3 and season-4) (not shown) for Maithon and Panchet reservoirs for projected scenarios depict that former is much less than the latter. Thus, operating the system with curtailed target demand (during season-3 and season-4) for Maithon and Panchet reservoirs as well as by trading off between demands (at site demand and demand at downstream Durgapur barrage being catered by Maithon and Panchet reservoirs) was another option to adopt for further improvement of the system performance Three variations of this system demand, referred to as CD-1, CD-2 and CD-3 are:

• CD-1—90 % of total projected demand—the trading off being 100 % at site projected demand for Maithon and Panchet reservoirs and 75 % of projected demand for Durgapur Barrage

• CD-2—75 % of total projected demand—the trading off being 100 % at site projected demand for Maithon and Panchet reservoirs and 50 % of projected demand for Durgapur Barrage

• CD-3—60 % of total projected demand—the trading off being 75 % at site projected demand for Maithon and Panchet reservoirs and 50 % of projected demand for Durgapur Barrage.

It may be noted that demand management strategy which involves supplying water at a rate below the desired one which has been specified for pertinent reservoirs (curtailed demand) as well as trading off between these demands, is being recognized as an essential complement to water supply management if fresh water is to be used in a sustainable manner (Brooks 2006). This may be carried out in practice by encouraging efficient use of resource in the sense by reducing the quantity of water required to accomplish a specific task, adjusting the nature of the task so that it can be accomplished with less water at user end.

The operational policies used for the presented study are narrated below for the sake of ready reference:

• Operational Policy HS: Simulation of the operation of the system with historical inflow data, normal storage and historical water demand

• Operational Policy 1: Simulation of the operation of the system with synthetically generated inflow data, normal storage and 50 % of demand projected for 2025.

• Operational Policy 2: Simulation of the operation of the system with synthetically generated inflow data, reallocated storage (as discussed above) and 50 % of demand projected for 2025.

• Operational Policies 3, 4 and 5 refer to simulations of the operation of the system with synthetically generated inflow data, normal storage and CD-1, CD-2 and CD-3 demands respectively.

Operational Policies 6, 7 and 8 refer to simulation of the operation of the system with synthetically generated inflow data, reallocated storage and CD-1, CD-2 and CD-3 demands respectively.

The above noted operation policies will, hereafter, be referred to as OP-HS, OP-1, OP-2, OP-3, OP-4, OP-5, OP-6, OP-7, and OP-8 respectively. The model was configured to run for the DVC reservoir system for the above noted policies.

Performance indices

The performance of the DVC system was evaluated with the help of ‘Performance Indices’ for four seasons separately namely, season 1 (1st June to 30th September), season 2 (full month of October), season 3 (1st November to 31st December), season 4 (1st January to 31st May) to take into account variability of inflow, demand and guide curve operation during the four seasons. These indices have proven useful for assessment of performance of reservoir system as well as for comparative analysis of general reservoir system operational policies (Milutin and Bogardi 1995; Joshi and Gupta 2009; Roy and Banerjee 2010). These are:

1. Quantity based reliability (RI₀): the ratio between volume of water released for meeting demand (S) and the target demand (D) over the simulation period considered.

2. Time based reliability (RI₁): the long-run probability that the system will be able to meet the full targeted demand over the given time period:

$${\text{RI}}_{1} \; = \;\frac{{T - \sum\nolimits_{t = 1}^{T} f_{t} }}{T}$$

(5)

3. Mean daily deficit (RI₂): the average magnitude of failures:

$${\text{RI}}_{2} \; = \;\frac{{\sum\nolimits_{t = 1}^{{T_{f} }} {DEF_{t} } }}{{T_{f} }}$$

(6)

4. Average failure period (RI₃): the average duration of the period the system is in a continuous failure mode:

$${\text{RI}}_{3} \; = \;\frac{{\sum\nolimits_{i = 1}^{{N_{f} }} {t_{f,i} } }}{{N_{f} }}$$

(7)

5. Resilience (RI₄): the longest duration of consecutive periods of failure:

$${\text{RI}}_{4} \; = \;\max_{{i \in N_{f} }} t_{f,i}$$

(8)

6. Maximum vulnerability (RI₅): maximum magnitude of failure event:

$${\text{RI}}_{5} \; = \;\max_{{t \in T_{f} }} {\text{DEF}}_{t}$$

(9)

7. Flood control index (RI₆): the ratio between the number of stages during which the river overflows its bank to the number of stages during which the pool level is in the flood control storage zone and releases are made in an attempt to draw the reservoir to the top of conservation pool without exceeding the designated channel capacity at the reservoir or at operational downstream control points plus the number of stages during which excess water is stored in the reservoir pool to avoid control point flooding over the simulation period considered (i.e., total number of stages). RI₆ takes the value ≤1 if failure occurred, zero otherwise.

f represents failure case, t refers to a time stage and failure at stage t is f _t ; f _t takes the value of one if a failure occurred, zero otherwise; i depicts a set of continuous sequence of stages with steady failure event, N _f represents the total number of sets of non-interrupted sequences of stages in which failure occured. The supply deficit at stage t is given by DEF _t . T and T _f represent the total number of stages and the total number of failure stages, respectively.

Results and discussion

A comparison of the mean and standard deviation (which is normally used as performance criteria) of the generated streamflow series and the historical streamflow series revealed that mean values of generated monthly flows (Table 3) for subbasins of reservoirs and barrage to be in close agreement with the corresponding historical values (range of discrepancy being 0.02–21 %). Higher discrepancies of 38.25 and 33.86 % in mean values of flow for the month of September for Maithon reservoir and for the month of February for Panchet reservoir, respectively were noted. Again, standard deviation values of generated streamflows were found to differ from the observed ones in a range of 0.22 % to 27.19 %—higher discrepancy values (32.31 % to 39.67 %) were observed for generated flows for some months (Table 3). The results indicate that the estimated monthly streamflow data compares favorably well with the observed data and this generated monthly streamflow data has been used to generate corresponding daily flow data. Roy and Banerjee (2010) generated the monthly streamflow for Dwarakeswar river in eastern India by Thomas and Fiering model and concluded the suitability of the model to describe the streamflow on the basis of closeness of mean and standard deviation of generated and historical streamflow data (the ranges of discrepancies in the mean and sd values have been reported to be 0.45 to 7.69 % and 9.42 to 22.81 %, respectively).

Table 3 Discrepancy in mean and standard deviation values for the generated streamflow series

The estimates of the performance indices for the DVC system for OP-HS, OP-1, OP-2, OP-3, OP-4, OP-5, OP-6, OP-7, and OP-8 are shown in the (Fig. 4a–f; Table 4). The decrease of indices of quantity based reliability RI₀ (by 1 to 23 %— i.e., supplying decreased quantum of target water), time reliability RI₁ (by 2 to 19 %— i.e., decrease of the number of periods to fully satisfy the target water demand), increase of mean daily deficit RI₂ (by 121 to 408 %), average failure period RI₃ (by 67 to 263 %), resilience RI₄ (140 to 300 %—i.e., the operation policy performs worse in recovering rapidly from a failure period) and maximum vulnerability RI₅ (33 to 319 %—i.e., at least in one period, a larger portion of water demand could not be met), in general, for OP-1 for all seasons depict poor performance of the reservoir system in future years compared to that in historical years. Remarkably high decrease by (54–67 %), (65–74 %), (505–2000 %), (746–3442 %), (340–416 %) and (400–940 %) was noted for the estimates of the indices RI₀, RI₁, RI₂, RI₃, RI₄ and RI₅, respectively for OP-1.The poor performance is driven by high water requirement projected for future.

Fig. 4

a–f Average values of performance indices for reservoir system for historical and future scenario (for various operation policies)

Table 4 Average values of Performance Indices for reservoir system for historical and future scenario (for various operation policies)

The corresponding estimates of performance indices for OP-2 (with enhanced conservation storage) indicate improvement in the performance in season-3 and season-4 compared to that for OP-1(with increase of RI₀, RI₁ and decrease of RI₂, RI₃, RI₄ and RI₅) and this, in turn, depicts merit of reservoir storage reallocation policy (Table 4).

Again, OP-3 policy (with moderately modified demand and normal storage) showed slightly poor performance (with decrease of RI₀, RI₁ and increase of RI₂, RI₃, RI₄ and RI₅) with respect to OP-2 policy indicating that marginal curtailment of demand alone may not necessarily prove to be a good choice to improve the performance. However, OP-3 along with OP-4 and OP-5 policies show increasingly better performance (increase of RI₀ and RI₁ and decrease of RI₂, RI₃, RI₄, RI₅) of Maithon & Panchet reservoirs in respective seasons (compared to OP-1) for obvious reasons and both the OP-4 and OP-5 policies (with highly modified demand) also proved to be better than OP-2 policy.

Again, the performance of the system with OP-6, OP-7 and OP-8 policies (with enhanced conservation storage and modified demand) showed further improvement (with increase of RI₀, RI₁ and decrease of RI₂, RI₃, RI₄ and RI₅) over that for OP-2, OP-3,OP-4 and OP-5 policies and in respective seasons (Fig. 4a–f; Table 4). But still the performance was unable to be restored to that for OP-HS (Fig. 4a–f). This is due to the detrimental effect of increased demands as the reliability is limited by available inflow and high demand.

It may be noted that quantity based relaiability for all the cases was higher than time reliability for obvious reasons. It may also be noted that allocated demand meeting priority led to higher in-stream-flow reliability compared to M& I reliability. Further, it may be noted that integrated operation led to the marginal variation (1 to 5 %—not shown) of the performances of Tilayia,Konar and Tenughat reservoirs for all policies in spite of keeping them outside the purview of any modification. An inter seasonal comparison of reservoir performance (Fig. 4a–f; Table 4) reveals the performance to be better for season 1 (not shown) and season 3 compared to that for season 2 and season 4 (with performance in season 4 to be worse than that in season 2) for all operation policies. This may be attributed to sufficient inflow received by the reservoir system in season 1 (which spans over monsoon when 85–90 % of annual flow is received by the system) and to full/nearly full conservation storage available on first day of season 3 (as realized by Guide Curve limited operation). Again, Guide curve limited operation in season 2 and lack of inflow as well as almost exhausted storage in season 4 (which coincides with summer and end of water year) led to poor performance in respective seasons.

Again, 100 % reliability for flood control (zero value of index RI₆) for current as well as future synthetically generated scenarios for season 1 and season 2 for all the aforementioned policies may be attributed to DVC reservoir operation guideline which is always limited by flood control rule curves and foresight release decision adopted by HEC-5 model. The foresight release decision requires prior knowledge of future flows and thus makes release determinations in anticipation of future flow (days in advance) for controlling flood. It may further be mentioned that as is the normal case, no high flow was received by the system during season 3 and season 4 during the simulation period considered.

Considering commitment of DVC authority to cater various demands, policy which minimizes modification of aforesaid demands i.e., the policy OP-6, (with moderately curtailed target demand) with reasonably good reliability in the most critical season i.e., season 4 (quantity based reliabilities of 89, 47 and 91 % for at site demand of Maithon and Panchet reservoirs and for demand at Durgapur Barrage, respectively) (Fig. 4c) may be considered to be a viable option for improvement of the performance of the reservoir system. The associated other indices (resilience and maximum vulnerability) for the above noted cases are also reasonably good. Again, the policy OP-8 (with highly curtailed target demand), may be accepted if higher reliability of supply in season 4 (quantity based reliabilities of 94, 63 and 95 % for at site demand of Maithon and Panchet reservoirs and demand at Durgapur Barrage, respectively) (Fig. 4c) at low stipulated demand (i.e., at the cost of quantum of demand) be the criterion for reservoir operation.

Some related studies are quoted here. Joshi and Gupta (2009) reported decrease of volume reliability Index and time reliability index for supplying water for industrial, domestic and irrigation purposes with increasing minimum flow releases for Narmada River Reservoir System in India. Awadallah and Awadallah (2014) suggested a release policy which allows a reduction of half of the total pumping costs with only 3 % reduction in the water allocation reliability, as measured by the failure frequency of demand satisfaction and the average shortage index for a system of three dams, two pumping stations and two diversion structures located in the Upper-Chéliff (Algeria) in Northwest Africa. Jahanpour et al. (2014) reported for the Ekbatan Dam in Iran more desirable reliability and resiliency values for operating policy (which adopts optimization approach which is based on loss function which minimizes total deficit) than those for standard operating policy for the reservoir.

It may be concluded from the study reported herein that by carrying out marginal storage reallocation and curtailing requirement along with trading off between demands simultaneously (adopting OP-6), performance of system of reservoirs may be improved for synthetically generated future scenario with projected demand.

An, analysis of trade-off between the index RI₀ with other indices RI₁, RI₂, RI₃, RI₄ and RI₅ (Fig. 5) shows that RI₁ increases whereas RI₂, RI₃, RI₄ and RI₅ decrease with increase in RI₀ excepting for values of RI₀ (0.84, 0.89—Fig. 5a) and (0.52, 0.63—Fig. 5b) wherein RI₃, RI₄ and RI₅ increase. Similar variations have been observed for other reservoirs and pertinent water demands (not shown). In general, increase of RI₀ implies higher availability of water and correspondingly increase of RI₁ and decrease of RI₂, RI₃, RI₄ and RI₅. It may however, be noted that index RI₀ is related to quantum of water whereas the indices RI₁,RI₂,RI₃,RI₄ and RI₅ are related to number of failure stages. Thus combination of daily pattern of intermediate catchmental flow, upstream reservoir release and daily pattern of demand would determine the changes of RI_1, RI₂ RI₃, RI₄ and RI₅ with RI₀ and this is causing the change from the general trend. The EOP (end-of-period) storage (Fig. 6) on 31st May for Maithon and Panchet reservoirs was found to follow the same trend as that for performance indices for aforementioned scenarios.

Fig. 5

a, b Trade-off among different performance indices (average values) for municipal and industrial water demand of Maithon reservoir and irrigation water demand of Durgapur barrage, respectively

Fig. 6

Average EOP Storage on 31st May at Maithon and Panchet reservoirs for historical and future scenario (for various operation policies)

The study points out that performance of the DVC reservoir system is reasonably improved by adopting OP-6—all the performance indicators were found to yield good results. The only indicator that portrayed very poor estimate is the resilience indicator RI₄ (with a value of 98 days for Panchet reservoir at site demand which is caused by prolonged drought period in the inflow record). The finding also indicates that projected pace of development in the Damodar basin in the near future needs to be reduced, thereby keeping low level of associated demand of water and augmentation of resource would be necessary for meeting the full projected demand.

It may be noted that the various policies, discussed above, involve potential benefits that exist in operating the reservoirs in tandem for meeting demand. Reasonable benefit (an increase of time reliability by 90–120 %, decrease of resilience by 85–98 % was obtained in operating the Tenughat and Konar reservoirs in tandem with Panchet reservoir for meeting demand in season 4 for OP-6 (not shown). Again, improvement of performance (an increase of time reliability by 45–65 %, decrease of resilience by 80–91 %) was accrued when Panchet and Maithon reservoirs released water for meeting demand of Durgapur Barrage, located downstream with a foresight of 24 h (which has been used for the present study).

Conclusion

A simulation model for reservoir system operation, HEC -5, has been used to analyze the performance of the DVC reservoir system on the river Damodar in meeting future demand as well as controlling flood for historical and synthetically generated future scenario (with 50 % of demand projected for 2025) in order to develop an appropriate strategy for its operation. The future streamflow series for the river system was successfully generated by Thomas-Fiering method.The study revealed that simultaneous and judicious adoption of resource enhancement (marginal reallocation of reservoir storage capacity) and demand management strategies (curtailment of projected high water requirements and trading off between demands) may be a viable option for increasing the reliabilities, reducing resilience and vulnerability of the system.

This, in turn, indicates that augmentation of resource (i.e., increasing the conservation storage volume at the expenses of flood control storage volume for reservoirs or construction of additional reservoir in the DVC system) would be necessary for meeting the full projected demand. It may be noted that DVC project had originally envisaged the construction of another dam (other than the existing ones) at Balpahari on the Barakar river (upstream of existing Maithon dam). However, on account of financial and other reasons, the aforesaid scheme is yet to be implemented. The study also indicates towards adoption of reduced pace of development in the Damodar basin in the near future, thereby keeping low level of associated demand of water.

Thus, the study would provide an useful input to concerned authority that water demand management is as important as water supply management and that the former is highly required to complement additional water supply in the context of growing demand and dwindling resource.

One important feature of the HEC-5 model is that it assumes that future flows are known with certainty and thus makes release determinations in anticipation of future flow (days in advance) for meeting demand as well as for controlling flood. i.e., it uses foresight for meeting demand as well as for controlling flood. This should be taken into account while using results from such study for cases where knowledge of future flow is lacking.