A node-based layered graph approach for the Steiner tree problem with revenues, budget and hop-constraints

Abstract

The Steiner tree problem with revenues, budget and hop-constraints (STPRBH) is a variant of the classical Steiner tree problem. The goal is to find a tree maximizing the collected revenue, which is associated with nodes, subject to a given budget for the edge cost of the tree and a hop-limit for the distance between the given root node and any other node in that tree. In this work, we introduce a novel generic way to model hop-constrained tree problems as integer linear programs and apply it to the STPRBH. Our approach is based on the concept of layered graphs that gained widespread attention in the recent years, due to their computational advantage when compared to previous formulations for modeling hop-constraints. Contrary to previous MIP formulations based on layered graphs (that are arc-based models), our model is node-based. Thus it contains much less variables and allows to tackle large-scale instances and/or instances with large hop-limits, for which the size of arc-based layered graph models may become prohibitive. The aim of our model is to provide a good compromise between quality of root relaxation bounds and the size of the underlying MIP formulation. We implemented a branch-and-cut algorithm for the STPRBH based on our new model. Most of the instances available for the DIMACS challenge, including 78 (out of 86) previously unsolved ones, can be solved to proven optimality within a time limit of 1000 s, most of them being solved within a few seconds only. These instances contain up to 500 nodes and 12,500 edges, with hop-limit up to 25.

1 Introduction

The Steiner tree problem in graphs (SPG) is a classical problem in operations research, see e.g., [20, 21, 29] and the references therein. In the SPG, we are given a graph G(V, E) with edge costs $c:E \mapsto \mathbb {R}^+$ and a set of terminals $T \subseteq V$, and the goal is to find a tree of minimal cost, which contains all terminals. In this work, we consider a variant of the SPG known as the Steiner tree problem with revenues, budget and hop-constraints (STPRBH), whose definition is given below. The problems has been intensively studied in the last years using exact [7, 22, 27] and heuristic [6, 13, 14] approaches.

Definition 1

(The Steiner tree problem with revenues, budget and hop-constraints (STPRBH)) We are given an undirected graph $G=(V,E)$ with edge costs $c:E \mapsto \mathbb {R}^+$, node revenues $p:V \mapsto \mathbb {R}^+$, a dedicated root node $r \in V$, a hop-limit $H \in \mathbb {N}^+$ and a budget limit $B \in \mathbb {R}^+$.

A feasible solution of the STPRBH is a subtree $\mathcal {T}=(V_S \subseteq V, E_S \subseteq E)$ rooted at r, where every node in $V_S$ can be reached form the root r using at most H edges and the total cost of the edges in $E_S$ does not exceed B, i.e., $\sum _{e \in E_S} c_e \le B$. The goal is to find a feasible subtree $\mathcal {T}^*$ that maximizes the revenue defined as $\sum _{v \in V_S} p_v$.

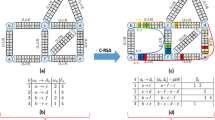
Figure 1 depicts an instance of the STPRBH and its optimal solution.

Fig. 1

a Graph of an instance of the STPRBH problem. Let $p_1=10,\,p_2=0,\,p_3=4,\,p_4=9,\,p_5=5$, the cost of the solid edges be one, and of the dashed edges be five. b The optimal solution for $H=2$ and $B=3$ has objective value 15 a Instance. b Solution

Our contribution In this work, we present a novel generic way to model hop-constrained tree problems as integer linear programs (ILPs) and apply it to the STPRBH. Our approach is based on layered graphs, a concept which has gained widespread attention in the last few years. On the one hand, layered graphs allow for significant improvements of computing times when compared to previously available extended formulations (see [19]). On the other hand, they are also shown to theoretically dominate most of the available extended formulations that model hop-constraints. Instead of modelling the problem on G, a layered graph is constructed such that for each layer $1\le h \le H$, a copy of the nodes of G is established, and nodes between two consecutive layers are connected whenever there exists a connection between them in G (for more details, see Sect. 2). The underlying problem is then formulated as a Steiner arborescence problem using arc variables on such obtained layered digraph. While this formulation often provides very good LP-bounds (see, e.g. [19]), the number of variables (which is O(H|E|)), often becomes prohibitive when the problem is formulated on larger graphs, or when larger hop-limits H are considered.

To overcome this latter drawback, we propose to project out the set of arc variables of the layered graph, resulting in a new formulation that comprises only node variables on the layered graph (along with node and arc variables on G). Whereas the standard layered graph approach involves O(H|E|) variables, our new model deals with $O(H|V| + |E|)$ variables only. Our models is compact, i.e., it requires only a polynomial number of constraints to ensure connectivity of the solution. However, we show that better bounds can be obtained by imposing an exponential number of subtour elimination constraints on G. Our model provides a good compromise between quality of obtained LP-bounds and the size of the underlying model. This approach of “thinning out” MIP models has been recently exploited in [10, 11] for solving Steiner trees and facility location problems, respectively. Note, however, that except from the high-level idea of deriving sparser MIP models to deal with large-scale instances, there are no direct similarities between the model presented in this paper and those studied in [10, 11].

A branch-and-cut-algorithm for the STPRBH derived from our new formulation solves most of the instances from the DIMACS Challenge [8] to provable optimality in a short time (often within a few seconds). This includes 78 (out of 86) instances for which the optimal solution has been previously unknown. Our framework won the category STPRBH in the challenge. The program is made available online under http://homepage.univie.ac.at/markus.sinnl/program-codes/stprbh/.

Outline of the paper Our paper is structured as follows: in Sect. 2, a short review of layered graphs is followed by the presentation of our generic new model together with valid inequalities. Section 3 contains a description of our solution framework, including a preprocessing phase and primal heuristics. Computational results are presented in Sect. 4. Section 5 concludes the work with a short summary and a discussion of future work. It points out a broader potential of the proposed “thinning out” approach for modeling hop- or diameter-constrained trees.

Previous work The STPRBH has been introduced by [7] where three branch-and-cut approaches have been presented: one based on Miller–Tucker–Zemlin constraints, one on Dantzig–Fulkerson–Johnson (also known as subtour-elimination) constraints, and one on hop-indexed formulation. Note that the latter formulation is based on hop-indexed edge variables, i.e., it can be viewed as a compact arc-based MIP formulation on a layered graph. Instances derived from sets B and C of the OR-library [2] have also been introduced in [7]. All instances from the set B and instances C1 to C5 have been solved to optimality with the approaches from [7]. These instances contain 500 nodes and 625 edges. However, the authors of [7] have demonstrated that no single model works well for all instances. In [6], the same authors proposed a greedy heuristic and a tabu search with some improvement procedures. They also reported some results for C6 to C20. These instances consist of 500 nodes and up to 12,500 edges. According to [6], for these instances, not even the root relaxation of the models presented in [7] could be solved within a time limit of two hours (in most of the cases). Branch-and-price approaches for the STPRBH have been studied by [27]. A lifted Miller-Tucker-Zemlin formulation and a formulation based on reformulation-linearization techniques were given in [22]. The two latter works provide computational results on the instances from sets B and C1 to C5, but offer no consistent speed up, when compared to [6]. Recently, a breakout local search algorithm (see [13]) and a memetic algorithm (see [14]) have been proposed. These two recent papers provide improved feasible solutions for some of the unsolved instances (C6 to C20). Some new instances based on graphs C16 to C20 are also introduced in [14].

2 Problem formulation and valid inequalities

Let $G_L=(V_L, A_L)$ be the layered graph associated with a rooted graph G(V, E) and hop-limit H. It is defined as follows (see, e.g., [19]): The node set $V_L=r \cup V^1 \cup V^2 \cup \ldots \cup V^H$, where $V^h$ contains a copy $v^h$ of all nodes $v \in V{\setminus } \{r\}$. Note that the root node r is the only node at layer zero. The arc set $A_L=A^1 \cup A^2 \cup \ldots \cup A^H$, where $A^h$ contains a directed copy (i, j) of an edge $\{i,j\} \in E$, iff $i \in V^{h-1}$ and $j \in V^h$.¹ Thus the layered graph has size $O(H(|V|+|E|))$. Figure  2 shows the layered graph associated with our exemplary instance from Fig. 1a and $H=3$.

Fig. 2

Layered graph associated with the graph from Fig. 1a and $H=3$

It has been shown in [19] that the optimal hop-constrained spanning/Steiner tree problem can be obtained by solving the Steiner tree problem on the layered graph $G_L$ with additional constraints that each Steiner/terminal node v has to be visited at most/exactly once across all layers. To this end, hop-constrained problems are formulated on $G_L$ by associating variables to the arcs $A_L$ of the layered graph, e.g., $x_{ij}^h$ is one, if arc $\{i,j\}$ is used on layer h (see, e.g., [19, 23]). While this usually gives models with strong LP-bounds, the size of the resulting MIP formulations soon becomes prohibitive. We thus propose to project out arc variables from the layered graph and model the hop-constraints by associating variables with the nodes $V_L$ of the layered graph.

To do so, we transform the graph G into a rooted digraph $D=(V, A)$, where A are the bidirected edges from E (incoming arcs to the root node are removed). We use the following sets of binary variables to model our problem (resp., generic hop-constraint trees)

$$\begin{aligned} x_{a}= & {} {\left\{ \begin{array}{ll} 1 &{}\text{ if } \text{ arc } a \text{ is } \text{ part } \text{ of } \text{ the } \text{ solution } \\ 0 &{} \text{ otherwise } \\ \end{array}\right. } \text{ for } a\in A;\\ y_{v}= & {} {\left\{ \begin{array}{ll} 1 &{}\text{ if } \text{ node } v \text{ is } \text{ part } \text{ of } \text{ the } \text{ solution } \\ 0 &{} \text{ otherwise } \\ \end{array}\right. } \text{ for } v\in V;\\ y^h_{v}= & {} {\left\{ \begin{array}{ll} 1 &{}\text{ if } \text{ node } v \text{ is } \text{ on } \text{ layer } h \text{ in } \text{ the } \text{ solution } \\ 0 &{} \text{ otherwise } \\ \end{array}\right. } \text{ for } v\in V {\setminus } \{r\}, 1\le h \le H. \end{aligned}$$

For $1\le i \le H-1$, let $H_i = \{ i, \dots , H\}$. Furthermore, let $\delta ^-(W)=\{(i,j) \in A: i \not \in W, j \in W\}$ and $\delta ^+(W)=\{(i,j) \in A: i \in W, j \not \in W\}$. Let $P=\{v \in V:p_v>0\}$ and $S=V {\setminus } \{P\cup \{r\}\}$. It can be easily seen, that there always exists an optimal solution to the STPRBH, where only nodes from P are leaf nodes. We will refer to P as set of profitable nodes, and S as Steiner nodes. For applying our model to other hop-constrained Steiner tree problems, this partition of the node set can be easily adapted, i.e., in case of the hop-constrained version of the classical Steiner tree problem, the partition is into terminal nodes and Steiner nodes.

Using this notation, we obtain a generic set of inequalities for modeling hop-constrained tree problems, denoted by (NODEHOP):

Constraints (CCuts), (Root) and (Indegr) comprise the cut-set formulation for the (prize-collecting) Steiner tree problem (see, e.g. [24]) and ensure that our solution contains an arborescence rooted at r. The remaining set of inequalities (NH-Link)-(HEnd-) deals with the hop-constraint: Node-hop link inequalities (NH-Link) ensure that if a node is part of the solution, it must lie on some layer. Hop-end inequalities (HEnd-) make sure that if a node lies on layer H, there can be no outgoing arc from it. Moreover, if the arc going from the root to node v is used, node v must lie on layer 1, which is ensured by (Root-Link). Hop-link constraints (HLink-) make sure that if a node v lies on layer $h-1$ ($2 \le h \le H$) and arc (v, w) is taken in the solution, then node w must lie on layer h. Note that crucial for the validity of our model is the tree/arborescence property: since every node only has one incoming arc (see constraints (Indegr)), the layer of each node is uniquely defined. Thus, constraints (CCuts) to (Binary) ensure in a generic way that the solution is an arborescence, satisfying the hop-constraint.

Using the generic model NODEHOP, it is easy to obtain the following formulation for the STPRBH:

The objective function (obj) ensures maximization of the revenue, while constraint (Budget) makes sure that a solution does not exceed the given budget B. Our model contains $|A| + (H+1)|V|$ variables, and an exponential number of connectivity constraints (CCuts). Next, we show that even a compact formulation obtained by replacing (CCuts) with a smaller family of constraints, provides a valid model for the STPRBH.

Theorem 1

Let sNODEHOP denote the compact model obtained from NODEHOP by replacing constraints (CCuts) with generalized subtour elimination constraints of size two:

$$\begin{aligned} x_{vw}+x_{wv}\le y_w, \quad v,w \in V \end{aligned}$$

(GSEC2)

This compact model is valid for the STPRBH.

Proof

Let $(x,y,y^h) \in$ sNODEHOP be the optimal solution of sNODEHOP and let Sol be the graph associated with this solution. We show that Sol is connected, does not contain cycles and does not violate the hop-limit.

In-degree constraints (Indegr), together with inclusion of the root (with in-degree zero), and constraints (GSEC2) ensure that the number of nodes in Sol is the number of arcs plus one. In-degree constraints ensure that there cannot be isolated nodes, except maybe the root node. Sol is cycle-free because each node has to be associated to exactly one layer $h, 1 \le h \le H$. A cycle in Sol would imply (due to inequalities (HLink-)) that there will be a node v in the cycle with $y_v^h = y_v^\ell = 1$, for $1\le h < \ell \le H$, which violates inequality (NH-Link). Hence, the resulting solution is cycle-free, with the number of edges being one less than the number of nodes, which implies that Sol is a tree.

It only remains to show that for every node $v\in Sol$, there exists a directed path from r to v using at most H arcs. Assume there is a node $v\in Sol$ for which the above condition does not hold. This is however a contradiction with constraints (HLink-) and (HEnd-), which concludes the proof. $\square$

In the following we provide some valid inequalities for the proposed new model NODEHOP. All inequalities except the ones in the last paragraph, i.e., (hop)-flow-conservation constraints, are also valid when our model is adapted to hop-constrained spanning tree problems, i.e., problems where $S=\emptyset$.

Hop-link inequalities First, note that in both constraints (HLink-) and (HEnd-), the value 1 can be down-lifted to $y_v$. The constraints still remain valid, since any of $y^{h-1}_v, y^{H}_v$ and $x_{vw}$ set to one also implies that $y_v$ is set to one.

Moreover, for any arc (v, w), constraints (HEnd-) can be made redundant (for integer solutions) by replacing inequalities (HLink-) with a lifted version with $y^H_v$ added to the left-hand-side. This is summarized in the following result:

Theorem 2

Let $h \in H_2$ and $(v,w) \in A, v\ne r$. Then the hop-link inequality

$$\begin{aligned} y^H_v+y^{h-1}_v +x_{vw}\le y_v+ y^{h}_w, \quad \forall (v,w) \in A, v \ne r \end{aligned}$$

(HLink)

is valid for NODEHOP.

Moreover, if $H\ge 3$, for any arc (v, w), constraints (HLink-) and (HEnd-) can be replaced by (HLink) for $2\le h \le H$.

Proof

First, we show the validity of the constraints, when they are added to NODEHOP (i.e., (HLink-) and (HEnd-) remain in the model). Observe that only one of $y^H_v+y^{h-1}_v$ can be one, due to (NH-Link). Suppose $y^H_v$ is zero, then the inequality reduces to (HLink-). Suppose $y^H_v$ is one, then $x_{vw}$ must be zero due to (HEnd-).

Now we assume all (HLink-) and (HEnd-) are replaced by constraints (HLink). The first argument of the previous proof still works, for $y^H_v$ zero, then the inequalities reduces to (HLink-). It now remains to show that the presence of the complete set of inequalities is enough to force $x_{vw}$ to zero for the case that $y^H_v$ is one. Thus, suppose both $y^H_v$ and $x_{vw}$ are one. Then for any constraint (HLink) for the given arc (v, w), the left-hand-side is two (and due to the assumption $H\ge 3$, there exist a least two constraints). However, due to (NH-Link), for only one h, we can have that $y^h_w$ is one, and thus for only one constraint (HLink) the right-hand-side can be two, which is a contradiction. $\square$

Generalized hop-link inequalities Using constraint (NH-Link) corresponding to node v, inequality (HLink) for an arc $(v,w), v \ne r$ and a given layer $h: 2\le h \le H$ can be rewritten as

$$\begin{aligned} x_{vw}\le y^{h}_w + \sum _{k \in H_1, k \ne (h-1), k\ne H} y^k_v \end{aligned}$$

(1)

It has the intuitive meaning that if arc (v, w) is in the solution, it either ends at layer h (and thus has started at layer $h-1$), or it must have started at some other layer smaller than H and other than $h-1$. Consider now another layer $l\ne h$: Inequality (1) is valid, because when arc (v, w) ends at layer l, it must have started at layer $l-1$ and there is $y^{l-1}_v$ on the right-hand-side of (1).

To motivate the generalization of these inequalities, observe that when the arc (v, w) ends at some layer $\ne l, h$, the variable $y^{l-1}_v$ must be zero in a valid solution. Moreover, when arc (v, w) ends at layer l, the variable $y^{l}_w$ must be one in any feasible solution. Thus it follows that $y^{l-1}_v$ can be replaced by $y^{l}_w$ in constraint (1) and the constraint remains valid. Generalizing this idea further, we observe that for each layer $h\ge 2$, in the summation on the right-hand-side, we must either include $y_v^{h-1}$ or $y_w^h$. This brings us to the following family of inequalities:

Theorem 3

Let P be the family of binary functions $P = {\mathbb {B}}^{|H_2|}, p \in P$ and $(v,w) \in A, v\ne r$. Then the generalized hop-link inequality

$$\begin{aligned} x_{vw}\le \sum _{h \in H_2} (p_h y^{h-1}_v+ (1-p_h) y^{h}_w) \end{aligned}$$

(g-HLink)

is valid for NODEHOP.

Proof

Clearly, when node w lies on layer 1 it must be connected to the root node and $x_{vw}$ must be zero. Thus suppose there exists a feasible solution, where node w lies on some layer $k: 2\le k\le H, x_{vw}$ is one, i.e., the arc (v, w) is used and the right-hand-side of (g-HLink) is zero. Since node w lies on layer k and the arc (v, w) is used, it follows that node v must lie on layer $k-1$. This implies that both $y^{k-1}_v$ and $y^k_w$ are one. Due to the definition of the function $p, p_k=1$ or $p_k=0$ and consequently, we have either $y^{k-1}_v$ or $y^{k}_w$ on the right-hand-side and thus the right-hand-side is one, which is a contradiction to the assumption that the inequality is violated. $\square$

For each arc $(v,w) \in A$, constraints (g-HLink) can easily be separated in O(H) time: given a fractional solution $({{\tilde{x}}}, {{\tilde{y}}}, {{\tilde{y}}}^h)$, for each layer $h \ge 2$, we consider the sum $\sum _{h \in H_2} \min \{ {{\tilde{y}}}_v^{h-1}, \tilde{y}_w^{h} \}$. If the obtained sum is smaller than ${{\tilde{x}}}_{vw}$, a violated constraint is detected.

Let us now consider a pair of inequalities of type (g-HLink), one associated to (v, w) and the other to (w, v). Let ${{\hat{p}}}$ and ${{\tilde{p}}}$ be the functions from P defining the first and second inequality, respectively. Summing up this pair of inequalities, we obtain

$$\begin{aligned} x_{vw}+x_{wv}&\le \sum _{h \in H_3} (({{\hat{p}}}_{h}+(1-\tilde{p}_{h-1})) y_v^{h-1} + ({{\tilde{p}}}_{h}+(1-{{\hat{p}}}_{h-1}))y_w^{h-1})\\&\quad +{{\hat{p}}}_2 y_v^1+{{\tilde{p}}}_2 y_w^1 +(1-{{\tilde{p}}}_{H}) y_v^{H}+(1-{{\hat{p}}}_H) y_w^{H} \end{aligned}$$

Thus, depending on the functions ${{\hat{p}}}$ and ${{\tilde{p}}}$, the coefficients of $y^h_v$ and $y^h_w$ are zero, one or two in the resulting inequality. Since $x_{vw}+x_{wv}\le 1$ (this follows from inequalities (CCuts) and equalities (Indegr), respectively from inequalities (GSEC2)), all coefficients of value two can be down-lifted to one.

Thus, the validity of the new derived families of inequalities presented in the following two theorem follows immediately. The first set of inequalities is obtained with ${{\hat{p}}}_{h}=\tilde{p}_{h}={\left\{ \begin{array}{ll} 1 &{}\quad \text {if } h \text { is even} \\ 0 &{}\quad \text {otherwise} \end{array}\right. }$ and the second one with ${{\hat{p}}}_{h}={{\tilde{p}}}_{h}={\left\{ \begin{array}{ll} 0 &{}\quad \text {if } h \text { is even} \\ 1 &{}\quad \text {otherwise} \end{array}\right. }$.

Theorem 4

Let $(v,w) \in A, v\ne r$. Then the odd two-arc hop-link inequality

$$\begin{aligned} x_{vw}+x_{wv}\le \sum _{h \in H_1, h \text { odd}} (y^{h}_v+y^{h}_w) \end{aligned}$$

(o2AHLink)

is valid for NODEHOP.

Theorem 5

Let $(v,w) \in A, v\ne r$. Then the even two-arc hop-link inequality

$$\begin{aligned} x_{vw}+x_{wv}\le \sum _{h \in H_2, h \text { even}} (y^{h}_v+y^{h}_w) \end{aligned}$$

(e2AHLink)

is valid for NODEHOP.

For each pair of arcs $(w,v),(v,w) \in A$, constraints (o2AHLink) and (e2AHLink) can easily be separated in O(H) time in a similar fashion to inequalities (g-HLink).

Cut inequalities on the layered graph If a node w lays on a layer h, there obviously must be at least one node $v\ne w$ at layer $h-1$ in the solution. This leads to the following family of node-hop-index inequalities:

$$\begin{aligned} \sum _{(v,w) \in A} y^{h-1}_v \ge y^{h}_w \end{aligned}$$

(2)

Such inequalities (expressed in terms of arc-variables on the layered graph) are commonly used in the hop-indexed models for hop-constrained problems (see, e.g. [15]). They represent a compact way of ensuring a connectivity of a solution. However, these hop-indexed compact models are known to suffer from weak lower bounds. In state-of-the-art approaches, connectivity constraints are therefore modeled using cut-set inequalities on layered graphs (see, e.g. [19, 23]).

By considering a modified layered graph, where nodes are split into directed arcs, it is not hard to see that one can consider cut-set inequalities derived on the layered graph using $y^h$ and x variables. Preliminary computational experiments, however, showed that addition of such type of inequalities in general was not beneficial for our problem, due to the high cost of separation (which involves max-flow computations on this modified layered graph). Instead, we use a subfamily of these cut-set inequalities, that we refer to as node-arc-cut-inequalities and that we illustrate next.

Observe first that if the input graph is complete, node-hop-index inequalities will be in general very weak, since the left-hand-side contains all nodes on layer $(h-1)$ in this case. Clearly, also the following inequality holds for any $h\ge 2$ and node $w\ne r$, since it is a weaker version of inequalities (CCuts) for $W=\{w\}$:

$$\begin{aligned} \sum _{(v,w) \in A, v\ne r} x_{vw} \ge y^h_w. \end{aligned}$$

(3)

Observe that in both (2) and (3), the right-hand-side is the same, and we sum over all arcs on the left-hand-side. Hence, we can derive a more general family of inequalities, which contains both (2) and (3) as a special case.

Theorem 6

Let R be the family of functions $R = {\mathbb {B}}^{|A|}$ and $q \in R, w \in V$ and $2\le h\le H$. Then the node-arc-cut-inequalities

$$\begin{aligned} \sum _{(v,w) \in A, v \ne r} (q_{vw}x_{vw}+(1-q_{vw})y^{h-1}_v) \ge y^{h}_w \end{aligned}$$

(NACut)

are valid for NODEHOP.

Proof

Suppose there exists a feasible solution, where $y^{h}_w$ is one, i.e., node w lies on layer h, and the left-hand-side is zero. Since the node lies on layer h, there must be an incoming arc (v, w) from some node v lying on layer $h-1$, thus both $y^{h-1}_v$ and (v, w) must be one. One of these variables is on the left-hand-side of constraint (NACut), and thus the left-hand-side is one, which concludes the proof. $\square$

Constraints (NACut) can be separated in polynomial time as follows: given a fractional solution $({{\tilde{x}}}, {{\tilde{y}}}, \tilde{y}^h)$ and a node w and layer h, consider all nodes v, such that $(v,w)\in A$, and calculate the sum $\sum _{v: (v,w) \in A} \min \{ {{\tilde{x}}}_{vw}, {{\tilde{y}}}^{h-1}_v\}$. If the resulting sum is smaller than the LP-value of $y^h_w$, a violated inequality is obtained.

There is an interesting connection between the constraints (NACut) and constraints (g-HLink), which can be derived as follows. For a fixed $v'$ and w, let $q \in R:=\{q_{v'w}=0;q_{vw}=1, \forall v\ne v'\}$. Consider the aggregation of (NACut) over all $2\le h \le H$. We obtain

$$\begin{aligned} \sum _{(v,w) \in A, v\ne v',r} (H-1) x_{vw} +\sum _{h \in H_2}y^{h-1}_{v'} \ge \sum _{h \in H_2} y^{h}_w. \end{aligned}$$

Since the right hand side can be at most one, we can downlift the coefficient $(H-1)$ on the left hand side to one. Using equation (Root-Link), we obtain $x_{rw}+\sum _{(v,w) \in A, v\ne v',r}x_{vw}+\sum _{h \in H_2}y^{h-1}_{v'} \ge \sum _{h \in H_1} y^{h}_w$. This can be further rewritten using equations (Indegr) and (NH-Link) to get $x_{rw}+\sum _{(v,w) \in A,v'\ne v,r}x_{vw}+\sum _{h \in H_2} y^{h-1}_{v'} \ge \sum _{(v,w) \in A}x_{vw}.$ Canceling out the x-variables on both sides, we arrive at

$$\begin{aligned} \sum _{h \in H_2} y^{h-1}_{v'} \ge x_{v'w}, \end{aligned}$$

which is an inequality of the family (g-HLink).

Flow-conservation constraints The so-called flow-conservation constraints (FlowC), which have been shown to strengthen the directed (prize-collecting) Steiner tree cut formulation, (see, e.g., [21, 24]) are easily seen to be valid for NODEHOP.

$$\begin{aligned} x(\delta ^-(v)) \le x(\delta ^+(v)), \quad \forall v \in S \end{aligned}$$

(FlowC)

The constraints ensure (in the x-space) that no node in S can be a leaf node in a solution. They can be generalized in a version involving $y^h$-variables in a similar fashion to (NACut).

Theorem 7

Let F be the family of functions $F = {\mathbb {B}}^{|A|}$ and $f \in F, v \in S$ and $2\le h\le H$. Then the hop-flow-conservation-inequalities

$$\begin{aligned} \sum _{(v,w) \in A} (f_{vw}x_{vw}+(1-f_{vw})y^{h}_w) \ge y^{h-1}_v \end{aligned}$$

(HFlowC)

are valid for NODEHOP.

Proof

Suppose there exists a feasible solution, where $y^{h-1}_v$ is one, i.e., node v lies on layer $h-1$, and the left-hand-side is zero. However, since the node v is a Steiner node, there always exists an optimal solution, where v is no leaf node. Thus, there must be an arc (v, w) to some node w lying on layer h in the solution, thus both $y^{h}_w$ and (v, w) must be one. One of these variables is on the left-hand-side of constraint (NACut), and thus the left-hand-side is one, which concludes the proof. $\square$

3 The solution framework

We have implemented a branch-and-cut algorithm based on our model, using the state-of-the-art commercial solver CPLEX 12.6. Before the branch-and-cut algorithm gets started, a preprocessing phase, as presented in Sect. 3.1 is performed. Moreover, a primal heuristic (described in Sect. 3.2) is also part of our solution framework. Branching-priorities and details of the separation routines are described in Sect. 3.3. The selection of the valid inequalities to include in our framework is discussed in Sect. 4 together with the computational results.

3.1 Preprocessing

The aim of the preprocessing phase is to remove nodes, arcs and hop-indexed variables, which cannot be in an optimal solution. Moreover, the information gained in this phase also allows the lifting of some of the inequalities of the model. Let $dist (u,v)$ be the distance between two nodes u and v, this distance can be calculated with the help of a breadth-first-search (BFS). Moreover, let $dist (v,P) = \min _{w \in P} dist (v,w)$ be the distance between v and a closest node from the profitable-node set P. Note that these distances are calculated on a digraph, since the directed root cost test may remove some arcs in one direction. Some of the following results use the fact that there always exists an optimal solution for STPRBH (and other Steiner tree problems), where no Steiner node $v \in S$ is a leaf.

Shrinking the size of the model Note that our model is defined on a digraph, while the problem is defined on an undirected graph. In our preprocessing, we first work on the undirected graph, and try to remove as much edges/nodes as possible, before we perform the transformation into the directed graph. The digraph is then further preprocessed. The preprocessing is comprised of the following tests:

• directed root cost test: If arcs (v, w) and (r, w) exist, and it holds that $c_{rw}\le c_{vw}$, arc (v, w) can be removed, since w can always be connected to the root node. This test has been described in [19] for the hop-constrained spanning tree problem. A variant of this test, denoted by undirected root cost test, can be done before the transformation into a directed graph: If edges $\{v,w\}, \{r,v\}$ and $\{r,w\}$ exist, and it holds that $c_{rv}\le c_{vw}$ and $c_{rw}\le c_{vw}$, edge $\{v,w\}$ can be removed.

• degree-one test: This is a classical test from Steiner tree literature (see, e.g., [9]), every Steiner node with degree-one can be removed. Note that the degree-two test, which combines two edges into one, is not possible in our setting due to the hop-constraints.

• start/end-layer test: Obviously, all variables $y^h_v$ with $h< dist (r,v)$, where r is the root node, can be removed. For a similar approach, see also [23]. By definition of $dist (v,P)$, if $v \in S$, we must cross at least $dist (v,P)-1$ layers in order to reach a node in P from v. It follows that all variables $y^h_v$ with $h>H- dist (v,P)$ can be removed. Consequently, all variables nodes v with $dist (r,v)+ dist (v,P) > H$, can be removed. Also, all arcs (v, w), with $dist(r,v)\ge H- dist (w,P)$ can be removed.

The preprocessing starts with the undirected root cost test, followed by the degree-one test. Then the graph is transformed in a digraph and the directed root cost test is applied followed by the start/end-layer test. Finally, the degree-one test is then done again, since the start/end-layer test may remove some nodes, which could allow the degree-one test to also remove some additional nodes. Note that due to the directed root cost test, we can end up with $| dist (v,P)- dist (w,P)|>1$ for two nodes $v,w \in S$ with an edge $\{v,w\}$ in the original graph since one of the arcs (v, w) or (w, v) may be removed.

Lifting inequalities based on preprocessing Preprocessing can be used to lift some of the valid inequalities. We demonstrate this on the family (HLink). First, observe that for any arc (v, w) with $dist(v,P)>0$, e.g., for all $v \in S$, the lifting by adding $y^H_v$, which has been done to obtain (HLink) from (HLink-) does not have any effect, since the start/end-layer test removed the $y^H_v$ variable. However, due to the information gained by the dist-calculation, some other variables $y^h_v$ could be added to the left-hand-side. Suppose we are given an arc (v, w) with $dist(w,P)>dist(v,P)$. Let $h^*(w)=H-dist(w,P)$, i.e., $h^*$ is the last layer, where w can lie, define $h^*(v)$ analogously. Thus, whenever, $y^h_v$ is in the solution for some $h\ge h^*(w)$, the arc (v, w) cannot be taken. Following the same argumentation as for the lifting of (HLink-) to (HLink) by adding $y^H_v$, the lifting works by adding $\sum _{k=h^*(w)}^{h^*(v)} y^k_v$ to the left-hand-side of (HLink-). The resulting lifted inequalities (l-HLink) are denoted by lifted hop-link inequalities.

$$\begin{aligned}&\sum _{k=h^*(w)}^{h^*(v)} y^k_v+y^{h-1}_v +x_{vw}\le y_v+ y^{h}_w, \quad \forall (v,w) \in A,\\&\quad v \ne r, dist(r,v)+1\le h \le h^*(v,w). \end{aligned}$$

(l-HLink)

where $h^*(v,w)=min(h^*(v),h^*(w))$. Recall that in case the interval for which the constraint would be defined is empty, the start/end-layer test has removed the variable $x_{vw}$. Note that the sum can only go to $h^*(v)$, since the other $y^h_v$ variables have been removed. Some caution must be taken, when the constraints (l-HLink) for a given arc only remain for one layer due to preprocessing. In this case, the validity of the lifting does not hold anymore, since it is based on the condition that at least two constraints (l-HLink) for an arc exist in the model. A (lifted) version of constraints (HEnd-) denoted by lifted hop-end inequalities (see (l-HEnd)) needs to be added in this case.

$$\begin{aligned} \sum _{k=h^*(w)}^{h^*(v)} y^k_v+x_{vw}\le y_v \end{aligned}$$

(l-HEnd)

Observe that for $dist(w,P)=0$, i.e., $w \in P$, the original version of (HLink) remains, since the sum boils down to $y^H_v$. Lifted versions of the families (g-HLink),(o2AHLink), (e2AHLink) follow immediately by using the same ideas, i.e., the summation only needs to be over the range, where no $y^h_v, y^h_w$ variables have been removed by preprocessing (respectively in the separation of these inequalities, the removed variables can be viewed as fixed to zero , and are always preferred to be “taken” in the separated inequality). This latter view can also be applied to the separation of inequalities (NACut) and (HFlowC).

In addition to this lifting above, for all flow-balance inequalities (FlowC), where both the indegree and the outdegree of v is one, the inequality can be replaced by equality.

3.2 Primal heuristic

Our primal heuristic is a modification of the improved version Prim-I [1] of the well-known Prim-based Steiner tree heuristic [28]. The heuristic works similar to Prim’s minimum spanning tree algorithm [26], which starts with some node (the root node r, in our case) and then greedily grows the solution tree Sol by adding the node $v \not \in Sol$, with minimum connection cost to Sol, i.e., the minimum cost edge $e=argmin\{c_{e=vs}: (v,s): v \in V{\setminus } Sol, s \in Sol\}$, until all nodes are added. In the Steiner tree case, the solution Sol is grown by greedily adding terminal nodes $t \not \in Sol$, with minimum connection cost, the connection cost is now not the cost of a single edge, but the cost from Sol to the terminal. When adding the chosen terminal to Sol, all the nodes on the paths are also added to Sol. We modified the algorithm Prim-I for the STPRBH, by taking the hop-limit and the budget into account. This can be easily achieved, since Prim-I works similar to Dijsktra’s shortest path algorithm: Whenever an arc is going to be considered as part of a shortest path to a profitable node, we check, if the hop-constraint is still fulfilled after adding the arc (note that for this check, the value $H{\text {-}}dist(v,P)$ can be used, instead of the hop-limit), if not, we ignore the connection offered by the arc. The budget-constraint is checked, whenever a profitable node is added, if it would be violated, we of course do not add the profitable node. Moreover, if the LP-value ${{\tilde{y}}}_v$ of a profitable node variable $v \in T$ is smaller than 0.001, we consider the profitable node as Steiner node in the algorithm. When using this algorithm as primal heuristic, we set the arc weights to ${{\bar{c}}}_a= c_a(1- {{\tilde{x}}}_a)$, where ${{\tilde{x}}}_a$ is the current LP-value of variable $x_a$. We have also experimented to take the information offered by LP-values ${{\tilde{y}}}^{h}_v$ into account for the arc weights, but in general this produced worse results. A simple local search consisting of exchange of leaf nodes is done at the end as improvement procedure. The algorithm is also used as starting heuristic, in this case, the original arc weights $c_a$ are used.

The primal heuristic is put in the heuristic callback of CPLEX, which gets called after each LP at the root node and at the end of each node in the branch-and-bound tree. Moreover, we also call it in the lazy constraint callback of CPLEX, this callback gets called, whenever CPLEX encounters an integer solution. Such integer solutions can be produced by internal heuristics of CPLEX (which we explicitly turned on). In case that we do not add all inequalities of NODEHOP in the beginning, but separate them on the fly, these solutions produced by CPLEX may violate some of the not-yet added constraints, but can be repaired to feasible solutions (e.g., if not all inequalities (l-HLink) are already added, CPLEX can set some $y^h$ to a wrong value). We thus aim to repair such a solution with a call to our primal heuristic. Moreover, we also try a simpler repairing procedure, which just consists of setting the right values for the $y^h$ variables (this of course will not work, if the heuristic solution violated the hop-constraint). If we are successful in repairing, we store the solution and add it to CPLEX at the next call of the heuristic callback.

3.3 Further enhancements

Branching priorities The branching priorities are set as following: Each variable $y_v$ is assigned priority $p_v+1+H$, each variable $y^h_v$ gets priority $H-h$ and arc variables are assigned priority zero. This setting is chosen, since we conjecture that the most important decision in the STPRBH is to decide, which nodes, especially nodes with positive revenue, are in the solution. Moreover, if a node v lies on a layer near the root node, it is likely to greater influence the structure of the solution, than v lying on a layer near H.

Details of the separation routines The presented families of inequalities are all of a large size, some of them are even of exponential size, thus it is not practicable to add (all of) them in the beginning of the branch-and-cut algorithm, but separate them on-the-fly, when they are violated by the solution of the current LP. The separation of (the lifted versions of) inequalities (g-HLink), (o2AHLink), (e2AHLink), (NACut) has already be discussed above, inequalities (l-HLink), (FlowC) and (HFlowC) can also be separated in polynomial time by inspection.

Inequalities (CCuts) are separated using a max-flow algorithm [5], when the LP-relaxation is fractional, and using a BFS when an integer solution is encountered. The max-flow separation is enhanced using minimum-cardinality cuts, and nested cuts, moreover, we only add back-cuts, i.e., the incoming cut in the profitable-node-component, when the separation gives back more than one potential cuts, see [21, 24] for more details. The profitable nodes are permuted before separation, so that we do not always separate to the same profitable node first, since using nested cuts changes the capacities for subsequent separations. Moreover, also in the fractional case, we “shrink” the connected components with arcs whose LP-values are set to one as follows. We perform a BFS starting from the root node and follow all arcs whose LP-value is equal to one. Separation is then performed only for profitable nodes not reachable this way. Once we have finished the separation for a profitable node, we again start a similar BFS from this node, and all profitable nodes reached this way are also not considered for separation. Additionally, before adding a cut, we check if the nodes outside the component, to which the cut is incoming, could provide enough revenue to construct a better solution than the current incumbent. If not, we replace the y-variable on the right-hand-side of the cut to add with one, since any optimal solution must take a node from this component.

4 Computational results

The algorithm is implemented in C++ and compiled using g++4.9.2 with option O3. The framework OGDF [25] is used for graph-data-structures and CPLEX 12.6 is used as ILP-solver. The dual simplex algorithm with steepest edge pricing was chosen to solve the LP-relaxations. The computational results are obtained using a single core of an Intel E5-2670v2 with 2.5 GHz and 64 GB RAM. We used a time limit of 1000 s for our testruns.

4.1 Instances

We tested our algorithm on the instances provided at the 11th DIMACS implementation challenge on Steiner trees, available at [8]. These instances have been proposed by [7, 14]. Both are based on the graphs from the sets B and C of the Steiner tree problem graphs of OR-lib [2]. The transformation into STPRBH-instances is done as follows:

• terminal nodes from the STP are used as profitable nodes by associating a random positive revenue to it (see Table 1); revenues for all Steiner nodes from the STP are set to zero, i.e., they remain Steiner nodes

• the budget B is determined as $\sum _{e \in E} c_e/b$, where b is a given input parameter

• a hop-limit H is given

Using this transformation, 414 instances have been created in [7, 14]—their basic properties are shown in Table 1.

Table 1 Instances from the DIMACS-homepage

Following [14], the instances can be grouped in five categories according to their difficulty.

• Group G1 contains all instances based on set B. They have been solved to optimality by exact algorithms [7, 27] (some of them also by [22]). The size of this group is 144.

• Group G2 contains the instances based on C01-C05. They have also been solved to optimality by exact algorithms [7, 27] (again, some of them also by [22]). The size of this group is 60.

The remaining three groups, based on larger (denser) graphs than G1 and G2, have only been tackled with heuristics so far.

• Group G3 contains instances proposed by [7], for which the trivial bound (namely the sum $\sum _{v \in P} p_v$) is the optimal solution value. For all G3 instances, heuristics from [7, 13, 14] were able to establish corresponding feasible (and, thus, optimal) solutions connecting all profitable nodes within the given budget. The size of this group is 124.

• Group G4 contains the remaining instances proposed by [7]. For these instances, the optimal solutions are unknown. The size of this group is 56.

• Group G5 contains the instances proposed by [14]. The optimal solutions for these instances are unknown. The size of this group is 30.

4.2 Studying the influence of the valid inequalities

In this section, we analyze the influence of the valid inequalities to the performance of the branch-and-cut approach. As a testbed for this analysis, we focus on G5 which is the most difficult group of instances. We consider the value of the LP-relaxation at the root node and the running time needed to obtain this value, as two main indicators for the usefulness of proposed valid inequalities.

We compare the following settings:

• basic: This is our initial model that consists of constraints (Indegr), (NH-Link), (Root-Link), (Budget), (FlowC), (GSEC2) and a constraint, that the root must have at least one outgoing arc (this is a special case of constraints (CCuts)). Inequalities (l-HLink) and (l-HEnd) are separated on the fly by enumeration, since preliminary runs showed that including all of them in the initial model slows down the performance.

• cut: This is basic enlarged by (CCuts) that are dynamically separated, and

• nacut: This is basic, enlarged by (CCuts) and (NACut), both of them being dynamically separated.

For these three settings, Figs. 3 and 4 show performance profiles considering the LP-gaps and the running time at the root node of the branch-and-cut tree, respectively. The LP-gaps are calculated with respect to the optimal/best known solution.

Fig. 3

Root relaxation gaps for three different settings

Fig. 4

Time to solve the root relaxation for three different settings

It can be seen from Fig. 3 that both (CCuts) and (NACut) improve the quality of LP-relaxation bounds. Comparing the running times needed to solve the root node relaxation, it turns out that there is a significant trade-off between the separation time required by (NACut), and the quality of attained bounds. More precisely, for 7 out of 30 instances, calculation of the LP-bounds at the root node has been aborted due to the imposed time limit. Nevertheless, the obtained bounds were always better than those achieved by basic and cut.

We have also investigated the influence of inequalities (g-HLink), (o2AHLink), (e2AHLink), (FlowC), (HFlowC) in this manner, however, we do not report detailed results in the above figures for sake of readability. It turned out that inequalities (g-HLink), (o2AHLink) and (e2AHLink) all help to improve the quality of LP-bounds. However, the improvement is rather marginal, at a very high cost of increasing the overall running time. On the other hand, inequalities (FlowC) and (HFlowC), did not help in improving the LP-gaps.

In these experiments, we often observed a tailing-off effect, i.e., subsequent separation and resolving of LPs did only marginally improve the gaps after a certain number of iterations. We thus implemented a tailing-off control for the cut-loop. If $ub_{prev}-ub_{cur}<\rho$, where $ub_{prev}$ is the bound obtained from the previous LP-relaxation, $ub_{cur}$ the bound obtained by the current one, and $\rho$ is a given parameter, we skip the separation routines and resort to branching. Figures 5 and 6 report the performance profiles concerning the obtained root relaxation gaps and associated running times for basic, cut and nacut with $\rho =0.0001$, respectively.

Fig. 5

Root relaxation gaps for three different settings with tailing-off control

Fig. 6

Time (in seconds) needed to solve the root relaxation for three different settings with tailing-off control

Compared to the settings without the tailing-off control the gaps do not change too much. On the other hand, the time needed to solve the root relaxation drastically decreases. This may be explained by the fact that only the y-variables appear in the objective function, and the continuous addition of violated inequalities mainly influences the values of the x and $y^h$ variables (without significantly changing the values of y-variables). A more sophisticated cut-loop scheme, like, e.g., in-out separation considered in [4, 12], could theoretically further improve the performance, however, we did not investigate this further, since the current tailing-off control already worked very well within the branch-and-cut algorithm, as it is demonstrated in the next section.

4.3 Main results

For our main runs, setting nacut was chosen, with the tailing-off parameter $\rho$ set to 0.0001. The global upper bound of the branch-and-cut tree is taken as $ub_{prev}$ for the tailing-off test. Note that (NACut) are added to CPLEX using the purgeable option—this option allows CPLEX to remove constraints, if it deems them as not helpful. The following general purpose cuts of CPLEX have been set to one (moderate generation of cuts): fractional, zero-half, cover, all the other cuts are left at the default parameter.

In this section we concentrate on 86 instances of groups G4 and G5, for which the optimal solution values were unknown prior to this work. The results for group G4 are given in Table 2 and for group G5 in Table 3. Tables for groups G2 and G3 are given in the appendix (Tables 4, 5, 6, 7). Note that our approach solves all instances from G2 and G3 to optimality, most of them already at the root node. Only a handful of instances from group G2 requires more than 10 s of computing time (but not more than 43 s), while for G3, the longest computing time is below 3 s.

Table 2 Results for group G4 of previously unsolved instances

Table 3 Results for group G5 of previously unsolved instances

Each table reports the obtained solution value ($sol.\ val$), which is shown in bold, if we have been able to prove optimality. The obtained global upper bound (UB) is also given (note that for the given instances, all costs/revenues are integers, thus we used $UB-sol.\ val<1$ as stopping criterion). In addition, the gap after the timelimit is provided $[Gap\%]$, as well as the root relaxation gap $[RGap\%]$. These gaps are given with respect to the best found solution value. If we have $UB-sol.\ val<1$, opt is written instead. Note that this does not mean that optimality is proven at the root node, since the optimal solution may have not been found yet. On the other hand, CPLEX in some cases is able to use problem-specific information to prove optimality even if the root relaxation gap is greater than one. Moreover, due to repeated presolving and potential variable fixing and general purpose cuts of CPLEX, the root relaxation gaps can be different to the results reported in the previous section, where we looked at pure LPs. The time (t[s]) needed to prove optimality is also reported. If we were not able to prove optimality within our time limit of 1000 s, the corresponding entry in the table is “-”. The entry tbest[s] contains the time when the best solution has been found and nodes gives the number of nodes in the branch-and-cut tree.

For instance group G4, we observe that only four of the 56 instances remain unsolved. Interestingly, these unsolved instances all have a hop-limit of 15 and a budget-divisor of 20. About half of the instances from this group can be solved within the root node, and (aside from the unsolved ones) only five instances need more than 60 s of computing time.

For instance group G5, also four instances remain unsolved — in contrast to group G4, three of the unsolved instances now have a hop-limit of 5, and only one has a hop-limit of 15. Again, about half of the instances from the group can be solved to optimality at the root node and (aside from the unsolved ones) only four instances need more than 100 s.

To summarize, out of 86 previously unsolved instances, only eight remain. As mentioned before, larger hop-limits are one of main bottlenecks for the exact methods considered in previous literature. The obtained results clearly demonstrate that our new approach deals very well with larger hop-limit, as we have been able to solve all instances from literature with a (largest considered) hop-limit of 25 to proven optimality.

5 Conclusion and outlook

The power of layered graphs has been recently demonstrated for many problems, including hop- and diameter-constrained spanning trees [19], hop-constrained connected facility location [23], or for problems that involve more general hop- or diameter-constraints (see, e.g., [16, 17]).

In this paper, we proposed a new extended formulation based on a layered graph for hop-constrained spanning/Steiner tree problems. Our formulation follows a “thinning out” idea proposed in [10, 11]: instead of using variables associated with arcs of the layered graph, our new model projects them out and relies only on variables associated to the nodes of the layered graph. Thus, the resulting MIP formulation is considerably smaller than the ones considered in previous literature, which allowed us to tackle instances based on larger graphs and/or hop-limits.

We applied the new model to solve the Steiner tree problem with revenues, budget and hop-constraints (STPRBH), which has been part of the DIMACS challenge [8]. A branch-and-cut approach based on our model allowed us to significantly improve results from the available literature. Previous to our study, 86 out of 414 available instances have been unsolved. We proved the optimality for all except eight out of these 414 instances, often within seconds. For these remaining eight instances, we improved the best known solutions.

We consider the following topics as important directions for the possible future research:

• The focus of our article was on STPRBH, with the aim of providing a simple (compact) model, which is able to solve (nearly) all available STPRBH instances, including previously unsolved ones, in very short time. However, it would be interesting to conduct a theoretical and computational comparison of our model against other formulations for the classical hop-constrained tree problems (i.e., the Steiner/spanning tree problems with the cost-minimization objective and without profits and budget constraints). For these latter problems, the most important models to be considered are the arc-based layered graph model from [19] and disaggregated Miller-Tucker-Zemlin-based formulations (see, e.g., [3]).

• It is worth mentioning that diameter-constrained spanning/Steiner tree problems can also be solved using our new modeling approach. It remains an open question how the proposed model relates with the recent formulation derived in the natural space of edge variables (see [18]), and with the arc-based layered graph formulation studied in [19].

• Finally, we believe that broader applications involving hop- and diameter-constrained trees (see above), especially problems with large-scale instances, might significantly benefit from the proposed “thinning out” approach.

Appendix: Detailed results for previously solved instances based on set C

See Tables 4, 5, 6 and 7.

Table 4 Results for group G2 of instances previously solved to optimality by other exact approaches

Table 5 Results for group G3 of instances previously solved to optimality by heuristics, 1/3

Table 6 Results for group G3 of instances previously solved to optimality by heuristics, 2/3

Table 7 Results for group G3 of instances previously solved to optimality by heuristics, 3/3