Optimal operating room scheduling for normal and unexpected events in a smart hospital

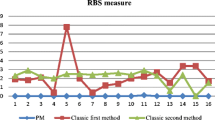
Abstract

A smart hospital can react to emergencies and unexpected events in real time. Emergencies occur frequently in hospitals, and the number of lives saved should be maximized. Because emergency patients disrupt established schedules of hospital operating room, proactive techniques should be employed to save as many lives as possible. In this study, three optimization models were developed for optimizing operating room scheduling during unexpected events and accommodating emergency patient surgeries in the established schedule. The first model (Model I) schedules emergency patients in newly opened rooms, whereas the second model (Model II) aims to assign emergency patients to untapped ranges; the third model (Model III) resequences elective and emergency patients in the room with the greatest free margin. This paper presents a real-life case study for illustration; the three models are adopted and the results are subsequently compared. In conclusion, the proposed models are expected to provide proactive plans for hospitals as well as enhance the performance and efficiency of operating rooms.

Appendices

Appendix 1

In Model I, the objective function is formulated as follows:

$$ Max\sum\limits_{w = 1}^{W} {\sum\limits_{v = 1}^{V} {U_{vw} } } $$

(5)

The model constraints are as follows:

• (i) The sum of surgery durations for all patients on any day must not exceed the regular working hours of room w. Let Dtot _v denote the duration of surgery for emergency patient v (in minutes) and N _w denote the regular working hours of room w on the emergency day (in minutes). OR availability is expressed mathematically as follows:

  $$ \sum\limits_{v = 1}^{V} {(U_{vw} } \times Dtot_{v} ) \le N_{w} ,\quad \forall w $$

  (6)

• (ii) The sum of surgery durations for day t scheduled for surgeon s must not exceed the availability of this surgeon in the hospital, as stated in Eq. (7). Let B _s denote the maximal working time of surgeon s on the emergency day (in minutes) and binary variable η _vs denote the assignment of patient p to surgeon s. Therefore,

  $$ \sum\limits_{v = 1}^{V} {\sum\limits_{w = 1}^{W} {(U_{vw} \times Dtot_{v} \times \eta_{vs} )} } \le B_{s} ,\quad \forall s $$

  (7)

• (iii) For assignment to room w, the required equipment should be available, as presented in Eq. (8), where λ _vw denotes the availability of the equipment required for patient v in room w on the emergency day.

  $$ U_{vw} \le \lambda_{vw} ,\quad \forall w,v $$

  (8)

• (iv) If the patient is in urgent need of surgical intervention on a specific day, then the latest start date is equal to the patient’s admission day; in this instance, the patient should be assigned. Let dint _v denote the emergency patient v due date; if the patient urgently requires surgery, then the patient should be assigned on the same day, as expressed in Eq. (9).

  $$ \sum\limits_{w = 1}^{W} {U_{vw} } = 1,\quad \forall v \in [1, \ldots ,V]/dint_{v} = t $$

  (9)

• (v) If the situation for patient v is not urgent, the due date of patient surgery (dint _v ) exceeds the scheduled date, and this patient is of second priority, then

  $$ \sum\limits_{w = 1}^{W} {U_{vw} } \le 1,\quad \forall v \in [1, \ldots ,V]/dint_{v} > t $$

  (10)

• (vi) The integrality constraint is formulated as follows:

  $$ U_{vw} \in \{ 0,1\} $$

  (11)

Appendix 2

The objective function of Model II is expressed as follows:

$$ Max \, \sum\limits_{v = 1}^{V} {\sum\limits_{p = 1}^{P} {\sum\limits_{j = 1}^{J} {\sum\limits_{w = 1}^{W} {x_{vpjw} } } } } \, $$

(12)

The model constraints are as follows:

• (i) Let u _pjw denote the untapped range between patients p and j in room w, and t _v denote the disruption time. The untapped range, into which patients can be assigned, must be calculated. Hence, any time unutilized before the disruption time is not considered, as stated in Eq. (13).

  $$ u_{pjw} = 0,\quad \forall p,j,w/p \ne j,st_{jw} < t_{v} ,st_{pw} + Dtot_{p} < t_{v} $$

  (13)

  However, emergency patients can be assigned into any unutilized time range after the disruption time. Then, the untapped range is the duration between the completion time of patient p (st _pw  + Dtot _p ) and the start time of patient j (st _jw ) when patient j follows patient p in room w, as presented in Eq. (14).

  $$ u_{pjw} = (st_{jw} - (st_{pw} + Dtot_{p} )) \times y_{pjw} ,\quad \forall p,j,w/j \ne p,st_{jw} \ge t_{v} ,st_{pw} + Dtot_{p} \ge t_{v} $$

  (14)

  When the disruption time occurs during an unutilized time, the untapped range is the duration between the disruption time and the start time of the following patient:

  $$ u_{pjw} = (st_{jw} - t_{v} ) \times y_{pjw} ,\quad \forall p,j,w/\;j \ne p,st_{jw} > t_{v} ,st_{pw} + Dtot_{p} < t_{v} $$

  (15)

• (ii) To assign emergency patients to an untapped range, the duration of the untapped range should be greater than or equal to the durations of surgery of the emergency patients, as expressed in Inequality (16).

  $$ \sum\limits_{v = 1}^{V} {x_{vpjw} \times Dtot_{v} } \le u_{pjw} \times y_{pjw} ,\quad \forall p,j,w/j \ne p $$

  (16)

• (iii) Each emergency patient should be treated once, and no placement can occur when patient p is the same as patient j, as presented in Inequality (17) and Eq. (18):

  $$ \sum\limits_{p = 1}^{P} {\sum\limits_{j = 1/j \ne p}^{J} {\sum\limits_{w = 1}^{W} {x_{vpjw} } } } \le 1,\quad \forall v $$

  (17)
  $$ \sum\limits_{p = 1}^{P} {\sum\limits_{j = 1/p = j}^{J} {\sum\limits_{w = 1}^{W} {x_{vpjw} } } } = 0,\quad \forall v $$

  (18)

• (iv) The assignment of emergency patients can take the value of 0 or 1; hence, $x_{vpjw}$ is a binary variable.

  $$ x_{vpjw} = \left\{ {0,1} \right\} $$

  (19)

Appendix 3

3.1 Sub-model III-A

For this sub-model, the following information must be identified: (1) the number of emergency and elective patients (P) and duration of regular OR opening time (T), (2) the required duration (Dtot _p ), latest start time (lst _p ), and readiness time (rt _p ) of each patient surgery, and (3) disruption time (t _v ), time from which the OR is available after the disruption time (H _w ), and OR readiness time (rd _w ). Let the decision binary variable q _pt determine patient assignment, which is equal to 1 if patient p is treated at time t, and 0 otherwise. Moreover, let st _p denote the start time of patient p. The binary decision variable y _pj denotes whether the surgery of patient p follows that of patient j in the selected OR, and it is equal to 1 if the surgery of patient j follows that of patient p, and 0 otherwise. Let P denote the set of waiting patients for treatment (including the emergency patients). The objective function is to maximize the total number of treated patients in the OR over the time horizon after the disruption time t _v . Then, the objective function is formulated as follows:

$$ Max \, \sum\limits_{p}^{P} {\sum\limits_{{t = t_{v} }}^{T} {q_{pt} } } $$

(20)

The constraints are formulated as follows:

• (i) Each patient should be treated once at most during the time horizon, as illustrated by Inequality (21).

  $$ \sum\limits_{{t = t_{v} }}^{T} {q_{pt} \le 1,\quad \forall p} $$

  (21)

• (ii) At each time t, only one patient can be assigned, as shown in Inequality (22).

  $$ \sum\limits_{p}^{P} {q_{pt} } \le 1,\quad \forall t \in \left. {\left\{ {t_{v} , \ldots ,T} \right.} \right\} $$

  (22)

• (iii) The emergency level of each patient must be satisfied by ensuring that the surgery start time of each patient is later than or equal to that patient’s latest surgery start time. The emergency level of patient p is satisfied by ensuring that the surgical procedure is started before that patient’s latest start time (lst _p ) as follows:

  $$ st_{p} - lst_{p} \sum\limits_{{t = t_{v} }}^{T} {q_{pt} } - M\left( {1 - \sum\limits_{{t = t_{v} }}^{T} {q_{pt} } } \right) \le 0,\quad \forall p \, $$

  (23)

• (iv) Surgical procedures should not be performed before patient p is ready. Let rt _p denote the readiness time for patient p; hence, the start time of the surgery of patient p should be at or after that patient’s readiness time, as expressed in Inequality (24).

  $$ st_{p} + M\left( {1 - \sum\limits_{{t_{v} }}^{T} {q_{pt} } } \right) \ge rt_{p} ,\quad \forall p \, $$

  (24)

• (v) Surgical procedures must be performed when the OR is ready. Let rd _w denote the readiness time for OR w; the surgery start time of patient p should be later than or equal to the readiness time of the OR, as formulated in Inequality (25).

  $$ st_{p} - rd_{w} \sum\limits_{{t = t_{v} }}^{T} {q_{pt} + M\left( {1 - \sum\limits_{{t = t_{v} }}^{T} {q_{pt} } } \right) \ge 0,\quad \forall p} $$

  (25)

• (vi) To verify OR availability after the disruption time, Inequality (26) is formulated to ensure that the start time of patient p occurs after the OR availability time and disruption time t _v :

  $$ st_{p} \ge H_{w} \times \sum\limits_{{t = t_{v} }}^{T} {q_{pt} } ,\quad \forall p $$

  (26)

• (vii) The precedence of surgical procedures should be respected. Therefore, Inequalities (27) and (28) are formulated as follows:

  $$ \sum\limits_{j \ne p}^{P} {y_{pj} \le 1,\quad \forall p} $$

  (27)
  $$ \sum\limits_{j \ne p}^{P} {y_{jp} } \le 1,\quad \forall p $$

  (28)

• (viii) Equation (29) is presented to impose that the number of assignments must be higher than one.

  $$ \sum\limits_{p}^{P} {\sum\limits_{j \ne p}^{P} {y_{jp} } } = \sum\limits_{p}^{P} {\sum\limits_{{t = t_{v} }}^{T} {q_{pt} - 1} } $$

  (29)

• (ix) When an assignment occurs, the start time of surgical care is equal to the time at which q _pt satisfies all model constraints, as presented in Eq. (30).

  $$ st_{p} = \sum\limits_{{t_{v} }}^{T} {t \times q_{pt} + M(1 - \sum\limits_{{t_{v} }}^{T} {q_{pt} ) ,\;\;\;\;\;\forall p} } $$

  (30)

• (x) No overlap occurs between any successive surgical procedures performed in the same OR, as demonstrated by Inequality (31).

  $$ st_{j} \ge st_{p} + y_{pj} \times Dtot_{p} - M(1 - y_{pj} ),\;\;\;\;\;\forall p,j $$

  (31)

• (xi) To ensure that the integrality of the variables is respected, Eq. (32) is formulated as follows:

  $$ q_{pt} = \left\{ {0,1} \right\},y_{pj} = \left\{ {0,1} \right\} $$

  (32)

When the submodel is solved, the start time for each patient (st _p ) is obtained in addition to the binary decision variable, q _vt , which denotes patient assignment and the matrix of precedence (y _pj ) for patients.

3.2 Sub-model III-B

The aim of this sub-model is to maximize emergency patient satisfaction. The satisfaction of each emergency patient is determined by considering the delay ($\delta_{{st_{pn} }}^{ + }$) between the time of patient assignment and patient readiness time. Having little or no delay in starting emergency patient surgical procedures is desirable; therefore, a smaller-the-better function is employed. Let $\mu (\delta^{ + }_{{st_{v} }} )$ denote the satisfaction function associated with $\delta_{{st_{v} }}^{ + }$; an emergency patient is fully satisfied when the surgery start time is within ($\alpha_{{st_{pn} d}}$) of his or her readiness time, after which the satisfaction decreases until it reaches 0 at ($\alpha_{{st_{pn} m}}$), as demonstrated in Eq. (33) and Fig. 5.

Fig. 5

Emergency patient satisfaction function in Sub-model III-B

$$ \mu \left( {\delta_{{st_{{p_{n} }} }}^{ + } } \right) = \left\{ {\begin{array}{ll} {1,} & {0 \le \delta_{{st_{{p_{n} }} }}^{ + } \le \alpha_{{st_{{p_{n} }} d}}^{ + } } \\ {\frac{{\alpha_{{st_{{p_{n} }} m}}^{ + } - \delta_{{st_{{p_{n} }} }}^{ + } }}{{\alpha_{{st_{{p_{n} }} m}}^{ + } - \alpha_{{st_{{p_{n} }} d}}^{ + } }},} & {\alpha_{{st_{{p_{n} }} d}}^{ + } \le \delta_{{st_{{p_{n} }} }}^{ + } \le \alpha_{{st_{{p_{n} }} m}}^{ + } } \\ \end{array} } \right. $$

(33)

The decision variable is $\mu (\delta_{{st_{{p_{n} }} }}^{ + } )$, which denotes patient satisfaction (the membership function of the occurred delay) and the occurred delay ($\delta_{{st_{{p_{n} }} }}^{ + }$). The objective function is to maximize total patient satisfaction, and this is mathematically expressed as follows:

$$ Max \, \sum\limits_{{p_{n} = 1}}^{{P_{n} }} {\mu \left( {\delta_{{st_{{p_{n} }} }}^{ + } } \right)} $$

(34)

To maximize total patient satisfaction, the minimum patient satisfaction ($\theta_{{P_{n} }}$), patient readiness time ($rt_{{P_{n} }}$), maximum delay during which a patient is satisfied ($\alpha_{{st_{{P_{n} }} m}}^{ + }$), and maximum delay during which a patient is 100 % satisfied ($\alpha_{{st_{{P_{n} }} d}}^{ + }$) must be determined. Furthermore, surgery start time ($st_{{P_{n} }}$) should be determined; however, this is obtained from sub Sub-model III-A.

The constraints of maximizing total emergency patient satisfaction are as follows:

• (i) The membership function of delay for each emergency patient should be higher than or equal to the minimum required satisfaction level, as formulated in Inequality (35).

  $$ \mu \left( {\delta_{{st_{{P_{n} }} }}^{ + } } \right) \ge \theta_{{P_{n} }} ,\quad \forall P_{n} $$

  (35)

• (ii) Patient satisfaction is determined by considering the delay in patient assignment, whose count starts from the patient readiness time ($rt_{{P_{n} }}$); the aim is to assign the patient once he or she is ready, as expressed in Eq. (36).

  $$ st_{{P_{n} }} + \delta_{{st_{{P_{n} }} }}^{ + } = rt_{{P_{n} }} ,\quad \forall P_{n} $$

  (36)

• (iii) The delay value ranges from the patient readiness time ($rt_{{P_{n} }}$) to the maximum allowed delay ($\alpha_{{st_{{P_{n} }} m}}^{ + }$), as expressed in Inequality (37).

  $$ 0 \le \delta_{{st_{{P_{n} }} }}^{ + } \le \alpha_{{st_{{P_{n} }} m}}^{ + } ,\quad \forall P_{n} $$

  (37)

• (iv) According to Fig. 4, if $\delta_{{st_{{P_{n} }} }}^{ + }$ is within the interval [0, $\alpha_{{st_{{P_{n} }} d}}^{ + }$], then $\psi_{{st_{{P_{n} }} }}^{1} = 1$ and $\psi_{{st_{{P_{n} }} }}^{2} = 0$. However, if $\delta_{{st_{{P_{n} }} }}^{ + }$ is within the interval [$\alpha_{{st_{{P_{n} }} d}}^{ + }$, $\alpha_{{st_{{P_{n} }} m}}^{ + }$], then $\psi_{{st_{{P_{n} }} }}^{1} = 0$ and $\psi_{{st_{{P_{n} }} }}^{2} = 1$. Therefore,

  $$ \psi_{{st_{{P_{n} }} }}^{1} + \psi_{{st_{{P_{n} }} }}^{2} = 1,\quad \forall P_{n} $$

  (38)

• (v) Because membership function of $\mu (\delta_{{st_{{P_{n} }} }}^{ + } )$ is nonlinear, a linearization procedure is employed. Let $\psi_{{st_{v} }}^{1}$ and $\psi_{{st_{v} }}^{2}$ denote binary variables, defined as Eqs. (39) and (40), respectively:

  $$ \psi_{{st_{{P_{n} }} }}^{1} = \left\{ {\begin{array}{ll} {1,} & {0 \le \delta_{{st_{{P_{n} }} }}^{ + } \le \alpha_{{st_{{P_{n} }} m}}^{ + } } \\ {0,} & {otherwise} \\ \end{array} } \right. $$

  (39)
  $$ \psi_{{st_{{P_{n} }} }}^{2} = \left\{ {\begin{array}{ll} {1,} & {\alpha_{{st_{{P_{n} }} d}}^{ + } \le \delta_{{st_{{P_{n} }} }}^{ + } \le \alpha_{{st_{{P_{n} }} m}}^{ + } } \\ {0,} & {otherwise} \\ \end{array} } \right. $$

  (40)

  The membership function can then be formulated as follows:

  $$ \psi_{{st_{{P_{n} }} }}^{1} + \left( {\frac{{\alpha_{{st_{{P_{n} }} m}}^{ + } }}{{\alpha_{{st_{{P_{n} }} m}}^{ + } - \alpha_{{st_{{P_{n} }} d}}^{ + } }}} \right) \times \psi_{{st_{{P_{n} }} }}^{2} - \zeta_{{st_{{P_{n} }} }} = \mu \left( {\delta_{{st_{{P_{n} }} }}^{ + } } \right),\quad \forall P_{n} $$

  (41)

  where $\zeta_{{st_{{P_{n} }} }} \ge 0$ and

  $$ \zeta_{{st_{{P_{n} }} }} = \left( {\frac{1}{{\alpha_{{st_{{P_{n} }} m}}^{ + } - \alpha_{{st_{{P_{n} }} d}}^{ + } }}} \right) \times \psi_{{st_{{P_{n} }} }}^{2} \times \delta_{{st_{{P_{n} }} }}^{ + } $$

  Maximizing $- \zeta_{{st_{{P_{n} }} }}$ equals minimizing $\zeta_{{st_{{P_{n} }} }}$; $\zeta_{{st_{{P_{n} }} }}$ can then be formulated as

  $$\begin{aligned}& \delta_{{st_{{P_{n} }} }}^{ + } \times \left( {\frac{1}{{\alpha_{{st_{{P_{n} }} m}}^{ + } - \alpha_{{st_{{P_{n} }} d}}^{ + } }}} \right) + \psi_{{st_{v} }}^{2} \times \left( {\frac{{\alpha_{{st_{{P_{n} }} m}}^{ + } }}{{\alpha_{{st_{{P_{n} }} m}}^{ + } - \alpha_{{st_{{P_{n} }} d}}^{ + } }}} \right) - \zeta_{{st_{{P_{n} }} }} \hfill \\&\quad\le \left( {\frac{{\alpha_{{st_{{P_{n} }} m}}^{ + } }}{{\alpha_{{st_{{P_{n} }} m}}^{ + } - \alpha_{{st_{{P_{n} }} d}}^{ + } }}} \right),\quad \forall P_{n} \hfill \\ \end{aligned} $$

  (42)

• (vi) The following constraints can be formulated using Eqs. (43) and (44):

  $$ \alpha_{{st_{{P_{n} }} d}}^{ + } \times \psi_{{st_{{P_{n} }} }}^{2} - \delta_{{st_{{P_{n} }} }}^{ + } \le 0,\quad \forall P_{n} $$

  (43)
  $$ \delta_{{st_{{P_{n} }} }}^{ + } - \alpha_{{st_{{P_{n} }} d}}^{ + } \times \psi_{{st_{{P_{n} }} }}^{1} - \alpha_{{st_{{P_{n} }} m}}^{ + } \times \psi_{{st_{{P_{n} }} }}^{2} \le 0,\quad \forall P_{n} $$

  (44)

The sub-model’s output includes patient satisfaction $\mu (\delta_{{st_{{P_{n} }} }}^{ + } )$ and the occurred delay ($\delta_{{st_{{P_{n} }} }}^{ + }$).

3.3 Sub-model III-C

This sub-model seeks to maximize elective patient satisfaction. The concerns of elective patients should not be postponed or set far from the appointment (APP); therefore, a nominal-the-better satisfaction function is employed. Let ($\delta_{{st_{{p_{e} }} }}^{ + }$) denote the amount of delay (positive deviation) before the elective patient appointment and ($\delta_{{st_{{p_{e} }} }}^{ - }$) denote the amount set forth (negative deviation) for the elective patient appointment. The highest satisfaction is reached when the time of appointment is unchanged, and satisfaction decreases until the delay is ($\alpha_{{st_{Pe} m}}^{ + }$) or the set forth is ($\alpha_{{st_{{P_{e} }} m}}^{ - }$), after which satisfaction is 0. The satisfaction function is given in Eqs. (45) and (46), as illustrated by Fig. 6.

Fig. 6

Satisfaction function a negative deviation and b positive deviation

$$ \mu \left( {\delta_{{st_{{p_{e} }} }}^{ - } } \right) = 1 - \frac{{\delta_{{st_{{p_{e} }} }}^{ - } }}{{\alpha_{{st_{{p_{e} }} m}}^{ - } }},\quad 0 \le \delta_{{st_{{p_{e} }} }}^{ - } \le \alpha_{{st_{{p_{e} }} m}}^{ - } $$

(45)

$$ \mu \left( {\delta_{{st_{{p_{e} }} }}^{ + } } \right) = 1 - \frac{{\delta_{{st_{{p_{e} }} }}^{ + } }}{{\alpha_{{st_{{p_{e} }} m}}^{ + } }},\quad 0 \le \delta_{{st_{{p_{e} }} }}^{ + } \le \alpha_{{st_{{p_{e} }} m}}^{ + } $$

(46)

The decision variables are elective patient satisfaction and delay: $\mu (\delta_{{st_{{p_{e} }} }} )$ and $\delta_{{st_{{p_{e} }} }}$, respectively. The objective function is to maximize the total satisfaction of a patient, and it is expressed mathematically as follows:

$$ Max \, \sum\limits_{{p_{e} = 1}}^{{P_{e} }} {\mu (\delta_{{st_{{p_{e} }} }} )} $$

(47)

The corresponding constraints are as follows:

• (i) Let $\theta_{{p_{e} }}$ denote the minimum required satisfaction level of elective patient p _e . Hence, the membership function of delay must be higher than or equal to the minimum required satisfaction level, as formulated in Inequality (48).

  $$ \mu (\delta_{{st_{{p_{e} }} }} ) \ge \theta_{{p_{e} }} ,\quad \forall p_{e} $$

  (48)

• (ii) Patient satisfaction is determined by considering the delay in the patient appointment; the aim is to avoid changing the appointment, as expressed in Eq. (49).

  $$ st_{{P_{e} }} - \delta_{{st_{{P_{e} }} }}^{ + } + \delta_{{st_{{P_{e} }} }}^{ - } = APP_{{P_{e} }} ,\quad \forall P_{e} $$

  (49)

  where the range of positive and negative deviations are as follows:

  $$ 0 \le \delta_{{st_{{P_{e} }} }}^{ + } \le \alpha_{{st_{{P_{e} }} m}}^{ + } ,\quad \forall P_{e} $$

  (50)
  $$ 0 \le \delta_{{st_{{P_{e} }} }}^{ - } \le \alpha_{{st_{{P_{e} }} m}}^{ - } ,\quad \forall P_{e} $$

  (51)

• (iii) At least one of the negative or positive deviations should be equal to 0. Therefore, two binary numbers are employed to express $\mu (\delta_{{st_{{p_{e} }} }}^{ - } )$ and $\mu (\delta_{{st_{{p_{e} }} }}^{ + } )$. Let $\psi_{{st_{{p_{e} }} }}^{1}$ and $\psi_{{st_{{p_{e} }} }}^{2}$ denote binary variables defined as Eqs. (52) and (53), respectively.

  $$ \psi_{{st_{{p_{e} }} }}^{1} = \left\{ {\begin{array}{ll} {1,} & {0 \le \delta_{{st_{{p_{e} }} }}^{ - } \le \alpha_{{st_{{p_{e} }} m}}^{ - } } \\ {0,} & {otherwise} \\ \end{array} } \right. $$

  (52)
  $$ \psi_{{st_{{p_{e} }} }}^{2} = \left\{ {\begin{array}{ll} {1,} & {0 \le \delta_{{st_{{p_{e} }} }}^{ + } \le \alpha_{{st_{{p_{e} }} m}}^{ + } } \\ {0,} & {otherwise} \\ \end{array} } \right. $$

  (53)

  The membership function can then be formulated as shown in Eqs. (54) and (55).

  $$ \mu \left( {\delta_{{st_{{p_{e} }} }}^{ - } } \right) = \psi_{{st_{{p_{e} }} }}^{1} \times \left( {1 - \frac{{\delta_{{st_{{p_{e} }} }}^{ - } }}{{\alpha_{{st_{{p_{e} }} m}}^{ - } }}} \right) = \psi_{{st_{{p_{e} }} }}^{1} - \left( {\frac{{\psi_{{st_{{p_{e} }} }}^{1} \times \delta_{{st_{{p_{e} }} }}^{ - } }}{{\alpha_{{st_{{p_{e} }} m}}^{ - } }}} \right) $$

  (54)
  $$ \mu \left( {\delta_{{st_{{p_{e} }} }}^{ + } } \right) = \psi_{{st_{{p_{e} }} }}^{2} \times \left( {1 - \frac{{\delta_{{st_{{p_{e} }} }}^{ + } }}{{\alpha_{{st_{{p_{e} }} m}}^{ + } }}} \right) = \psi_{{st_{{p_{e} }} }}^{2} - \left( {\frac{{\psi_{{st_{{p_{e} }} }}^{2} \times \delta_{{st_{{p_{e} }} }}^{ + } }}{{\alpha_{{st_{{p_{e} }} m}}^{ + } }}} \right) $$

  (55)

  However, a linearization procedure is required. Let

  $$ \zeta_{{st_{{p_{e} }} }}^{1} = \left( {\frac{1}{{\alpha_{{st_{{p_{e} }} m}}^{ - } }}} \right) \times \psi_{{st_{{p_{e} }} }}^{1} \times \delta_{{st_{{p_{e} }} }}^{ - } ,\quad \zeta_{{st_{{p_{e} }} }}^{2} = \left( {\frac{1}{{\alpha_{{st_{{p_{e} }} m}}^{ + } }}} \right) \times \psi_{{st_{{p_{e} }} }}^{2} \times_{{st_{{p_{e} }} }}^{ + } $$

  (56)

  Maximizing $- \zeta_{{st_{{p_{e} }} }}^{1}$ equals minimizing $\zeta_{{st_{{p_{e} }} }}^{1}$; $\zeta_{{st_{{p_{e} }} }}^{1}$ can then be formulated as follows:

  $$ \zeta_{{st_{{p_{e} }} }}^{1} \ge \left( {\frac{1}{{\alpha_{{st_{{p_{e} }} m}}^{ - } }}} \right) \times \delta_{{st_{{p_{e} }} }}^{ - } - \left( {1 - \psi_{{st_{v} }}^{1} } \right) $$

  (57)

  Similarly,

  $$ \zeta^{2}_{{st_{{p_{e} }} }} \ge \left( {\frac{1}{{\alpha^{ + }_{{st_{{p_{e} }} m}} }}} \right) \times \delta^{ + }_{{st_{{p_{e} }} }} - (1 - \psi^{2}_{{st_{v} }} ) $$

  Therefore,

  $$ \mu (\delta_{{st_{{p_{e} }} }} ) = \psi_{{st_{{p_{e} }} }}^{1} + \psi_{{st_{{p_{e} }} }}^{2} - \zeta_{{st_{{p_{e} }} }}^{1} - \zeta_{{st_{{p_{e} }} }}^{2} ,\quad \forall p_{e} $$

  (58)

• (iv) The following constraints are formulated in a similar manner.

  $$ \delta_{{st_{{p_{e} }} }}^{ - } - \alpha_{{st_{{p_{e} }} }}^{ - } \times \psi_{{st_{{p_{e} }} }}^{ - } \le 0,\quad \forall p_{e} $$

  (59)
  $$ \delta_{{st_{{p_{e} }} }}^{ + } - \alpha_{{st_{{p_{e} }} }}^{ + } \times \psi_{{st_{{p_{e} }} }}^{2} \le 0,\quad \forall p_{e} $$

  (60)
  $$ \psi_{{st_{{p_{e} }} }}^{1} + \psi_{{st_{{p_{e} }} }}^{2} = 1,\quad \forall p_{e} $$

  (61)