Introduction

In freshwater and near-coastal marine ecosystems, water temperatures provide an important constraint on ecological function (Coutant 1976). Examples include effects on fish spawning (Hotta et al. 2001), swimming performance (Myrick and Cech 2000), metabolism (Das et al. 2005; Scheller et al. 1999), and mortality (Coutant 1976; Johnson and Evans 1996) as well as effects on aquatic invertebrates (Vannote and Sweeney 1980; Ward and Stanford 1982). Specific examples of species of concern within the Sacramento–San Joaquin Delta that are sensitive to water temperatures at various points in the life cycles include the Sacramento winter run Chinook salmon Oncorhynchus tshawytscha (Baker et al. 1995), the Sacramento splittail Pogonichthys macrolepidotus (Moyle et al. 2004), and the delta smelt Hypomesus transpacificus (Bennett 2005; Swanson et al. 2000).

Climate change is projected to result in increases in mean annual air temperature of 2.2–5.8°C in the coming century averaged across the state of California (Loarie et al. 2008). An increase in air temperature will lead to earlier snowmelt, more precipitation falling as rain (vs. snow), and changes in the operation of California’s water delivery system (Barnett et al. 2008; Vanrheenen et al. 2004). To analyze the effects of climate change on fish populations, however, we require projections of water temperature under global warming scenarios.

In tidal systems, the water temperature at a particular location is determined by the interplay between atmospheric forcing, tidal dispersion, and riverine flows (Monismith et al. 2009). Formal models of tidal dispersion are not currently feasible for projections of temperature over centuries given the magnitude of the computational requirements. In view of this limitation, we have developed a statistical model of temperature in the Sacramento–San Joaquin Delta. Our emphasis in this paper is on understanding the dynamics of water temperatures and their possible effects on aquatic species.

Study Location

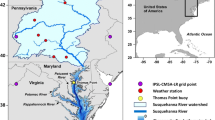
This study focuses on California’s Sacramento–San Joaquin Delta (the Delta) and nearby environs, which are located at the upstream end of the San Francisco Estuary. Detailed descriptions of the Delta can be found in Kimmerer (2004) and Lund et al. (2007). It consists of a network of channels (Fig. 1) that are fed by freshwater flow from a number of rivers that drain California’s Central Valley, most significantly the Sacramento and San Joaquin Rivers (Kimmerer 2004). The Delta serves as the hub of California’s water system, draining roughly 45% of the state’s area (Lund et al. 2007) and providing water supply to approximately two thirds of its population. In its unaltered state, the Delta was a system of sloughs and marshlands (both of which were open to influence from river flows and tidal effects), but currently it is a system of leveed, subsided farmlands separated by channelized tidal sloughs and rivers (Kimmerer 2004).

Fig. 1
figure 1

California’s Sacramento–San Joaquin Delta and environs. The Delta is forced by Sacramento River flow from the north, San Joaquin River flow from the south, and tides from San Francisco Bay in the west. The locations of the temperature stations are numbered; stations with circles had greater than 1 year’s worth of data. CIMIS weather stations are denoted with stars

Full size image

California’s water distribution system relies heavily on the Delta because reservoir releases must move through the Delta on their way to pumping stations for delivery to water users throughout the state (Lund et al. 2007). The most important of these stations are located in the southern Delta and provide water for the Delta Mendota Canal and the California Aqueduct, both of which carry water to municipal and agricultural users south of the Delta (Kimmerer 2004). The levees, dams, and diversions have drastically altered the hydrologic system from its native state. The ecology of the delta has been similarly altered, as it has responded to the changing hydrology as well as introductions of non-native fish, clams, and aquatic plants (Kimmerer 2004). Climate change will impact the Delta in a number of ways; examples include hydrologic change as the proportion of precipitation falling as snow declines in the Sierra Nevada mountain range (Vanrheenen et al. 2004), local heat budget adjustment to a warmer atmosphere, and estuarine response to sea level rise.

Data

Measured Water Temperature Data

We downloaded time series of measured water temperatures from the Interagency Ecological Program (http://www.iep.ca.gov), which receives the data from the California Department of Water Resources, the United States Geologic Survey, the California Data Exchange Center, and the United States Bureau of Reclamation, for locations throughout the Delta (Fig. 1). For many stations, water temperature data collection started in the mid-1980s and extends to the current time. The data have been collected at either 15-min intervals or hourly. For consistency among the data sets, we averaged the 15-min data to give hourly datasets. To handle outliers, we deleted all points outside 4 standard deviations from the mean of 20-h windows of the data. At locations where two or more agencies collected data, we averaged the data to create one dataset for each location. We calculated the daily maximum, average, and minimum water temperatures from these data for model calibration and verification.

Measured Forcing Data

We downloaded hourly air temperatures and insolation from the California Irrigation Management Information System (CIMIS; http://www.cimis.water.ca.gov) at seven locations within the Delta (Fig. 1; stations were Lodi, Brentwood, Manteca, Twitchell Island, Lodi West, Tracy, and Concord). We downloaded an additional six air temperature locations from the Interagency Ecological Program (locations 2, 9, 10, 13, 14, and 15 on Fig. 1). As an initial processing step, we removed physically impossible values (air temperatures less than −5°C or greater than 45°C; insolation less than 0 W/m2 or greater than the solar constant (1,368 W/m2; Rubin and Davidson 2001)) from both datasets.

To handle outliers in the air temperature data, we deleted all points outside 4 standard deviations from the mean of 20-h windows of the data. Model verification requires continuous forcing because the model output depends on the output from the previous time step. For this reason and for verification use only, we created a second air temperature dataset wherein gaps in the data shorter than 72 h were filled. We filled small gaps (<6 h) in this second dataset through linear interpolation. We filled longer gaps (<72 h) by first linearly interpolating and then adding a diurnal pattern defined by the diurnal cycles during adjacent (within 1 week) time periods spanning the same time of day as the gap. The daily cycle was defined by an average based on the time of day and was then added to the linear interpolation of the gap itself to produce synthetic data that match the daily patterns of the surrounding measured data. We did not fill gaps larger than 72 h.

We found that in the data of interest for these projections, the variation in air temperature and insolation across the locations was quite small. Therefore, we took the arithmetic mean of the data over the stations to provide representative values of air temperature and insolation for the Delta. Since the climate projections to be used to force the projections provided only daily maximum and minimum air temperature, we used the hourly data to produce these quantities for our historical domain.

Forcing for Water Temperature Projections

Projected scenarios of daily air temperatures were used to evaluate potential impacts of climate change on water temperatures in the Delta. The scenarios were derived from simulations of twenty-first century climate variations and trends by two global climate (or general circulation) models (GCMs) under each of two future global greenhouse gas emissions scenarios. The GCMs used here were the Geophysical Fluid Dynamics Laboratory’s (GFDL) CM2.1 coupled ocean–atmosphere GCM (Delworth et al. 2006) and the National Center for Atmospheric Research’s Parallel Climate Model (PCM) coupled ocean–atmosphere GCM (Washington et al. 2000). Daily temperatures from simulations by these two models, under A2 (rapidly accelerating) and B1 (eventually leveling) greenhouse gas emissions scenarios, were obtained from the Program for Climate Diagnosis and Intercomparison at the Lawrence Livermore National Laboratory (Meehl et al. 2007). The GCM simulations were made on global grids with about 2° to 3° latitude and longitude resolution (about 250 km at the latitude of the Delta), and thus, the original GCM scenarios were too spatially coarse for the purposes of this study. The GCM outputs were “downscaled” onto a 12-km grid over the conterminous USA by a method called constructed analogs (Hidalgo et al. 2008). This statistical downscaling method is applied to each day’s simulated climate condition in turn and is based on fitting a linear combination of historical weather patterns (aggregated onto the GCM grid) that best reproduces the GCM pattern for the day. The coefficients necessary to make this linear fit are then applied to high-resolution versions of the weather on the same historical days. This approach ensures that, day by day, the weather simulated by the GCM is faithfully carried down to the 12-km scale and tends to yield particularly realistic temperature relations across areas with sharp geographic gradients (Cayan et al. 2009). When applied to the historical record, as a validation exercise, the method reproduces daily temperature variations quite accurately on the 12-km grid given only historical temperatures as observed on the GCM grids as inputs (Hidalgo et al. 2008), indicating that the downscaled future-climate patterns are likely to also be realistic. The method was applied to climate simulations spanning the period from 1950 to 2100, to obtain daily, gridded temperature patterns of twenty-first century warming over California and the Delta.

The air temperature data were sub-sampled for the Delta region and then averaged to produce an equivalent forcing time series for 2000 though 2100 to those used during the calibration/verification stage. The data from the scenarios included maximum and minimum daily air temperatures. The climate projections did not provide insolation, so we derived the average insolation based on Julian day of the year. We extended this dataset to create a 100-year record under the assumption that insolation will be relatively constant over these climatic time scales.

Data Analysis

Temporal Variability

The daily water temperature data show strong yearly cycles as well as shorter time scale variation (Fig. 2). Although short-term variation exists, the yearly cycle dominates at all Delta locations. The amplitude of the yearly cycle, however, varies from year to year and between locations. This is most apparent starting in 1998 at Ripon (station 3), where, following a particularly wet winter season, the summer peak temperatures are reduced for 2 years (discussed further below). Although shorter time scale variations are evident, yearly variations (on the order of 15°C at the locations in Fig. 2) dominate the signal. These shorter time scale features are likely forced by a combination of short-term atmospheric conditions, local mixing, tidal advection of longitudinal temperature gradients, and possibly local precipitation.

Fig. 2
figure 2

Daily averaged water temperature at three locations from 1996 to 2003: a San Joaquin River at Antioch (station 2), b Ripon (station 3), and c Rio Vista (station 15)

Full size image

Spatial Variability

Once the water temperature data were processed, we performed a principal component analysis (PCA) on a subset of the data; the subset chosen was the eight stations (2, 3, 9, 10, 13, 14, 15, and 16) that had data from 1998 to 2002 because this was the longest uninterrupted dataset available. An overview of PCA can be found in Stacey et al. (2001); a more complete discussion is in Preisendorfer and Mobley (1988). This analysis is designed to decompose spatiotemporal data in such a way as to explain the maximum amount of total variance in the dataset in the first principal component (PC) and its associated temporal structure. Each principal component of a spatiotemporal dataset is a spatial structure which explains the maximum amount of variance possible within the dataset when combined with its associated temporal structure. The temporal structure, the amplitude of the principle component, defines the variability that is shared by the stations. Each successive principal component then explains the maximum amount of variability that remains in the dataset after removing the contributions of the previous principal components. All the PCs are mutually orthogonal to each other.

PCA at the eight locations that had data from 1998 through 2002 demonstrates the dominance of the yearly cycle in the temperature signal. Over 90% of the combined variance is described by the first principal component, whose amplitude represents the yearly cycle (Fig. 3). Overland and Preisendorfer’s (1982) test of significance (“rule N”) suggests that the higher modes of variation (PC2, 3, etc.) are not significant. In this test, the results of the PCA of the dataset of interest are compared to PCA of multiple random, normalized datasets to determine whether each principal component is significantly different from random noise. For this analysis, only PC1 passed rule N likely because autocorrelation in water temperatures caused so much variance to be captured in PC1, leaving so little left for higher modes of variation.

Fig. 3
figure 3

The amplitude of PC1 divided by its largest absolute value

Full size image

The PCA approach also displays spatial variability of the yearly cycle within the Delta (Fig. 4). Annual variability was strong at all locations, but, notably, PC1 is the strongest near the central Delta and the weakest toward the edges (north, south, and west); these are areas dominated by single water sources (Sacramento River, San Joaquin River, San Francisco Bay tides, respectively.) This indicates that these peripheral locations have annual cycles somewhat independent of the rest of the Delta. The time variability in the central Delta is complicated by the interaction of the three main water sources; the mixing of waters from these three water sources causes water temperatures in the central Delta to be near-uniform spatially.

Fig. 4
figure 4

Principal component 1 of the water temperature data for the years 1998–2002. The x-axis represents longitude and the y-axis represents latitude

Full size image

Methods

Water temperature has been modeled extensively over the years for a number of different locations. Modeling techniques have been split between deterministic models (Marce and Armengol 2008; Sinokrot and Stefan 1993; Uncles and Stephens 2001, for example) and statistical models (Caissie et al. 2001; Bradley et al 1998; Marce and Armengol 2008; Mohseni et al. 1999; Benyahya et al. 2007; Lemos et al. 2007, for example). Our approach here is to create a statistical model that is based on variables known to be important for deterministic models.

Development of Statistical Temperature Model

Assuming complete lateral and vertical mixing, the water temperature dynamics at a point in an estuarine channel can be defined

$$ \frac{{\partial {T_{\rm{w}}}}}{{\partial t}} + \frac{{\partial U{T_{\rm{w}}}}}{{\partial x}} = \frac{{\sum H }}{{{\rho_{\rm{w}}}z{C_{\rm{p}}}}} + \frac{\partial }{{\partial x}}{K_x}\left( {\frac{{\partial {T_{\rm{w}}}}}{{\partial x}}} \right) $$
(1)

where T w is water temperature, t is time, x is the direction of flow (along-axis), U is the velocity in the x-direction, H refers to atmospheric heat fluxes (defined below), ρ w is the density of water, z is the depth of the water column, C p is the specific heat of water, and K x is the dispersion coefficient in the x-direction. The atmospheric heat fluxes are broken down

$$ \sum {H = {H_{\rm{s}}} + } {H_{\rm{e}}} + {H_{{{\rm{l}} \downarrow }}} + {H_{{{\rm{l}} \uparrow }}} + {H_{\rm{sw}}}. $$
(2)

Following Fischer et al. (1979), Miyakoda and Rosati (1984), and Uncles and Stephens (2001), atmospheric heat fluxes (watts per square meter) into the surface of a body of water can be defined using bulk formulae:

$$ {\hbox{Sensible}}\;{\hbox{heat}}\;{\hbox{flux:}}\;{H_{\rm{s}}} = {\rho_{\rm{a}}}{C_{\rm{s}}}{C_{\rm{pa}}}W\left( {{T_{\rm{a}}} - {{\hbox{T}}_{\rm{w}}}} \right) $$
(3)
$$ {\hbox{Evaporative}}\;{\hbox{heat}}\;{\hbox{loss:}}\;{H_{\rm{e}}} = {\rho_{\rm{a}}}{C_{\rm{e}}}{L_{\rm{w}}}W\left( {{Q_{\rm{a}}} - {Q_{\rm{w}}}} \right) $$
(4)
$$ {\hbox{Long - wave}}\;{\hbox{heat}}\;{\hbox{radiation}}\;{\hbox{from}}\;{\hbox{water}}\;{\hbox{vapor:}}\;{H_{{{\rm{l}} \downarrow }}} = 5.18\; \times \;{10^{{ - 13}}}\left( {1 + 0.17{C^2}} \right){\left( {273 + {T_{\rm{a}}}} \right)^6} $$
(5)
$$ {\hbox{Long - wave}}\;{\hbox{heat}}\;{\hbox{loss}}\;{\hbox{from}}\;{\hbox{the}}\;{\hbox{water}}\;{\hbox{surface:}}\;{H_{{{\rm{l}} \uparrow }}} = - 5.23\; \times \;{10^{{ - 8}}}{\left( {273 + {T_{\rm{w}}}} \right)^4} $$
(6)
$$ {\hbox{Short - wave radiation from insolation}}:\;{H_{\rm{sw}}} = R\left( {1 - \alpha } \right) $$
(7)

For all heat fluxes, heating of the water column is represented by positive signs and cooling by negative. The symbols are defined as follows:

α :

Albedo (dimensionless)

C :

Fractional cloud cover (dimensionless)

C e :

Empirical exchange coefficient (∼1.5 × 10−3; dimensionless)

C s :

Empirical exchange coefficient (∼1.5 × 10−3; dimensionless)

C pa :

The specific heat of air (1.012 × 103 J/kg °C)

L w :

Latent heat of evaporation (2.4 × 106 J/kg)

ρ a :

The density of air (∼1.2 kg/m3)

R :

Insolation (W/m2)

Q a :

Atmospheric mixing ratio (see Fischer et al. 1979; dimensionless)

Q w :

Saturation mixing ratio at the ocean surface for T w (dimensionless)

T a :

Air temperature (°C)

T w :

Water temperature (°C)

W :

Wind speed at 10 m (m/s)

Typical values of calculated atmospheric heat fluxes within the Delta (Table 1) show the dominance of the long-wave and short-wave radiation terms. Bartholow (1989) observed that river water temperatures are typically not influenced by reservoirs more than 25–30 km upstream. This suggests that longitudinal gradients in water temperature are likely to be small and contributions from terms dependent on this gradient (advection and diffusion) are small by the time a water parcel reaches the Delta. Thus, combining Eqs. 1 and 2 and eliminating terms, we can write:

$$ \frac{{{\rm d} {T_{\rm{w}}}}}{{{\rm d} T}} \cong \frac{{{H_{{{\rm{l}} \downarrow }}} + {H_{{{\rm{l}} \uparrow }}} + {H_{\rm{sw}}}}}{{{\rho_{\rm{w}}}zCp}} $$
(8)

Or simplified even further:

$$ \frac{{{\rm d} {T_{\rm{w}}}}}{{{\rm d} T}} \cong f\left( {{T_{\rm{a}}},{T_{\rm{w}}},R} \right) $$
(9)

Equation 9 could be discretized as

$$ T(t) \cong T\left( {t - \Delta t} \right) + \Delta t\left( {f\left( {{T_{\rm{a}}},T,R} \right)} \right), $$
(10)

where T represents modeled water temperature; we drop the subscript w in order to emphasize that the model’s predicted water temperature will depend on the model’s output from the previous time step and not on measured values. Equation 10, although deterministic, is the basis for our statistical model. Based on the historical water temperature data, we applied a simple regression to relate the day’s water temperature to the air temperature and insolation from the same day and water temperature from the day preceding it:

$$ T(n) = a{T_{\rm{a}}}(n) + bT\left( {n - 1} \right) + cR(n) + d $$
(11)

where n is the day on which the temperature is being calculated, a is the coefficient on the current day’s air temperature, b is the coefficient on the previous days water temperature, c is the coefficient on the current day’s insolation, and d is a constant offset. This model can be used to model maximum, minimum, or average water temperatures. The insolation, R, used was the average insolation for each Julian day of the year.

Table 1 Typical values for the surface heat fluxes into (+) and out of (−) the water column for Stockton Ship Canal at Burns Cutoff (station 10)
Full size table

We used our regression model to accurately reconstruct historical water temperatures with a minimal amount of data needs or computational cost. To verify the model, we calculated regression coefficients for Eq. 11 using the first half of the dataset (the calibration period), then used these coefficients to force the model during the entire dataset (both calibration and verification periods). To project water temperatures for the coming century, we calibrated with the entire historical dataset and forced with the downscaled climate data and the annual insolation cycle.

Performance Metrics

We measured model performance through the root mean squared error (RMSE), the coefficient of determination (R 2), and the Nash–Sutcliffe coefficient (NSC). The first gives an idea of the magnitude of the errors. The latter two quantify how well the model performed on the whole.

The final metric, the Nash–Sutcliffe coefficient, has been used widely to evaluate the performance of hydrologic models and is defined (Nash and Sutcliffe 1970) as

$$ {\hbox{NSC}} = 1 - \frac{{\sum {_{{i = 1}}^N{{\left( {{O_i} - {P_i}} \right)}^2}} }}{{\sum {_{{i = 1}}^N{{\left( {{O_i} - O} \right)}^2}} }}, $$
(12)

where O represents observed data with N realizations and P represents predicted data. Values of NSC range from −∞ to 1.0. Higher values indicate better agreement. A value of zero indicates that the predicted values are no better than the mean of the observations as a predictor; negative values indicate that the observed mean is a better predictor. The NSC has been criticized as a metric because it (like R 2) gives too much weight to outliers. Additionally, Garrick et al. (1978) have argued that it is possible to get high values for the NSC with poor models while good models do not score much higher.

Results

Calibration and Verification of Statistical Temperature Model

Figure 5 presents time series of the calibration and verification periods from a long-term record on the San Joaquin River at Antioch (station 2). The annual cycle is clearly well-predicted, as are shorter time scale variations, particularly weekly to monthly fluctuations. A more difficult test is shown in Fig. 6, for which temperature data were only collected during the spring at San Joaquin River at Prisoner’s Point (station 5); the model was still able to capture the annual cycle sampled at the end of the verification period. This is most likely because the range of the data was close to the annual range in temperature.

Fig. 5
figure 5

Calibration (a) and verification (b) at the San Joaquin River at Antioch (station 2). The measured values are indicated with the solid line; the modeled values are indicated with the gray line. The calibration R 2 was 0.981; verification R 2 was 0.978

Full size image
Fig. 6
figure 6

Calibration (a) and verification (b) at San Joaquin River at Prisoner’s Point (station 5). The measured values are indicated with the solid line; the modeled values are indicated with the gray line. R 2 values are 0.976 for calibration and 0.974 for verification

Full size image

The model performed very well at locations where more than 1 year of data were available for calibration. After locations with less than 1 year of data were removed, the model fit the data well (Table 2) with R 2 values greater than 0.930 (and generally over 0.965) and NSC values greater than 0.890 (and generally over 0.950) for verification periods for all locations except Ripon (station 3), which is on the Stanislaus River and farther from tidal influence than the other stations.

Table 2 This table lists calculated performance metrics for each variable with at least 1 year of calibration data for both calibration and verification periods. Cal calibration, Ver verification, RMSE root mean squared error, R 2 coefficient of determination, NSC Nash–Sutcliffe coefficient
Full size table

Projections of Water Temperatures for Climate Scenarios

Model projections predict long-term changes in water temperatures throughout the Delta (model coefficients are reported in Table 3). Figure 7 shows an example of these projections, showing projected water temperatures on the San Joaquin River at Antioch (station 2) under PCM A2 forcing. In this particular case, both the yearly high and low water temperatures increase over the 100-year time horizon.

Table 3 Model coefficients and their 95% confidence intervals at locations with at least 1 year of calibration data
Full size table
Fig. 7
figure 7

One hundred-year projection of daily max water temperatures on the San Joaquin River at Antioch (station 2) under PCM A2 forcing

Full size image

Discussion

Model Limitations

One major concern is the ability of a statistical model to project water temperatures in a changing system. The model predicts the seasonal cycle as well as capturing much of the short-term variability compared to measured data. These seasonal fluctuations (the dominant mode of variability) are much larger than the long-term trends expected with climate change. On the other hand, increases in water temperatures could lead to increases in evaporative cooling and ultimately cause a leveling off of water temperatures near some maximum (Mohseni et al. 1999). While this dynamic is not included in the model, the model is effective at predicting the maximum temperatures contained in the historical record of the current regime.

While this approach has been successful at reproducing water temperatures at locations of long-term records, the local spatial variability of the system is not captured. The statistical approach essentially projects the water temperature that would be measured at the instrumentation site. It is unclear if those temperature measurements are representative of the local or regional water temperature. Depending on the station and the method of deployment of the instrument, there are likely to be both lateral and vertical gradients in water temperature that would reduce the applicability of the results for locations other than the instrument sites. Further, variation between stations may not be linear but may change abruptly at channel junctions or other Delta features. Finally, all of the long-term stations are located along either the Sacramento or San Joaquin River channels, so the applicability of the results to other sloughs and channels in the Delta is unclear.

Flow Effects

The model skill evident in our verification periods indicates that riverine flows are not required to effectively predict water temperatures in the Delta on long time scales. However, on shorter time scales, large flows create features that the model is unable to accurately forecast.

Although flow effects on water temperatures are, to great extent, overwhelmed by atmospheric influences, flow does appear to have significant effects over shorter time scales, and some events have longer-term implications. We performed a PCA on each year from 1998 to 2002 individually to evaluate the inter-year stability of the annual cycle. The comparison of the first PC (the yearly cycle) for these years (Fig. 8) shows a temporary increase in the strength of this PC over the western Delta and a weakening of this PC at Ripon (station 3), the most eastern station and the one farthest from tidal influence. This shift comes in conjunction with a large El Niño with accompanying large flows during the winter of 1997–1998. The western stations have higher PC1 for 1998 than for other years, perhaps because high flows of that year forced a downstream shift of the interaction of Bay and river waters, making the western stations more like the up-estuary reaches of the Delta during a typical year. The western stations recovered their normal yearly cycle within 1 year; Ripon does not re-align with the Delta until 2002. This is presumably the result of elevated reservoir releases that persisted for more than a year following the large flows of 1997–1998.

Fig. 8
figure 8

PC1 for each year from 1998 to 2002 taken individually for the stations that had data for that time period (2, 3, 9, 10, 13, 14, 15, and 16). The x-axis represents longitude and the y-axis represents PC1

Full size image

Another notable example of this effect is at Rio Vista (station 15) on the Sacramento River. Water temperatures were lower than predicted during the exceptionally high flows of the 1997–1998 winter, but once the water temperatures began to warm in the spring, the model prediction again matched the observations (Fig. 9). Bartholow’s (1989) observations indicate that it is unlikely that this divergence in model performance is caused by influence from upstream dam releases; more likely, this divergence is due to either local precipitation and run off or changes in mixing in the north Delta region. Through model calibration using data that span multiple years, the model is optimally designed to capture as much variability as possible during a typical year for a location, including accounting for the relative contributions of San Francisco Bay and riverine waters at a site. During high flow events, riverine influences on Delta water temperatures increase while Bay influence decreases. This affects the thermal dynamics at a site across years, just as it affects it within years. Further, the inundation of the Yolo Bypass (a flood plain conveyance that is active during high flows) may have altered the thermal dynamics in the vicinity of Rio Vista, which is near the outflow of the Bypass. In the Rio Vista example (Fig. 9), high flows are associated with lower temperatures during model divergences for a period of a couple of months. However, once spring warming began in March, the model converges on the observed temperatures, including two warming–cooling events in March and April. Notably, the model also diverges during the following summer prior to cooling during the fall.

Fig. 9
figure 9

Short-term model deviations due to large flows on the Sacramento River at Rio Vista (station 15). The measured values are indicated with the solid line; the modeled values are indicated with the gray line. The circle highlights model deviations from measurements during the winter of 1997–1998

Full size image

Another process that might cause short-term anomalies in model performance is the effect of flows on thermal dispersion within the Delta. Monismith et al. (2009) found a strong positive correlation between the thermal dispersion coefficient and river flow along the San Joaquin River. A visual analysis of the residuals of our model (Fig. 10) indicates that flows may have an effect on the performance of the model in this area of the Delta; however, the correlation between residuals and flows (R 2 = 0.14) is low enough that integrating flow into the model is unlikely to improve performance. Similar analyses at locations on the Sacramento River show no correlation between residuals and flow (max R 2 = 0.07).

Fig. 10
figure 10

Potential flow effects on model performance at Stockton Ship Channel at Burns Cutoff (station 10). The gray line represents the model residuals (measured temperature minus modeled temperature) at station 10; the thick black line represents San Joaquin River flows nearby at the Garwood Bridge

Full size image

Temperature Trends

Under the selected climate-change scenarios, both daily maximum and daily minimum water temperatures are expected to increase. This increase varies from one scenario to another and from one location to another within each scenario. For example, a comparison of the predicted yearly cycle of the daily average temperature at Rio Vista (station 15) in 2097-2099 yields very different results for each of the four scenarios (Fig. 11). Under all of our climate scenarios, the yearly cycle peaks later in the year than in 1997–1999, with the GFDL A2 scenario giving a sharper, higher peak than the others. All four projections are considerably warmer (∼3–6°C) in late summer than 1997–1999.

Fig. 11
figure 11

Projected yearly cycle of water temperatures at Sacramento River at Rio Vista (station 15) averaged from 2097 to 2099. The mean of the measured water temperatures at the same location from 1997 to 1999 is included for comparison

Full size image

Ecological Implications

One informative way to evaluate the increase in water temperatures is to look at ecological thresholds. The Delta smelt, a federally listed threatened species endemic to the Delta, has high mortality above a temperature of about 25°C (Bennett 2005). If we look at the number of days at a location that the daily maximum temperature exceeds the 25°C threshold, then temperature trends (from an ecological standpoint) become easier to see. Although all areas are projected to warm in response to increased air temperatures, the ecological effects would not be uniform across the Delta (Fig. 12). Notably, the Sacramento corridor shows the greatest change with respect to this threshold mostly because other areas of the Delta are already frequently exceeding the threshold.

Fig. 12
figure 12

Spatial variability in heating. Dot area is proportional to the average number of days per year exceeding 25°C (the Delta smelt’s thermal limit) at each location under GFDL A2 forcing. The black dots represent the measured data; the dark gray dots are for 2010–2030; the light gray dots are for 2070–2090

Full size image

Delta smelt require water temperatures between about 15°C and 20°C during spring months for spawning, and juvenile delta smelt are stressed between 20°C and 25°C during the summer (William Bennett, personal communication). Since the spawning temperatures occur during the spring warming cycle and the rate of warming is relatively insensitive to climate-change scenarios, the number of days within these ranges does not change much in response to climate change (Fig. 13), but the timing can be affected. If the timing of the temperature variations in these ranges were to drift out of phase with other ecological variables (i.e., flows, sunlight, etc.), it could have an important impact on the populations of these species. Over the 100 years projected here, the model predicted shifts on the order of 10–15 days of the median day of the spawning period under three of our four scenarios (Fig. 14). The fourth scenario, GFDL A2, would cause the greatest shifts, on the order of 25 days.

Fig. 13
figure 13

Long-term shift in water temperatures on the Sacramento River at Rio Vista (station 15) under GFDL A2 forcing. Using projected temperatures, each day is grouped as it impacts the Delta smelt: spring spawning (daily average temperatures from 15°C to 20°C in light gray), stress (daily average temperatures from 20°C to 25°C in dark gray), and lethal (daily maximum temperatures >25°C in black)

Full size image
Fig. 14
figure 14

Projected shift in the median day of the spawning period due to temperature on the Sacramento River at Rio Vista (station 15). The median day of the spawning period was calculated for each year under each scenario. The medians were smoothed with a 10-year running average

Full size image

Summary

We present a simple, computationally efficient model for water temperatures within the Sacramento–San Joaquin Delta. The statistical model is based on physical principles; calibration and verification demonstrate the ability of our statistical approach. The model’s skill allows consideration of the long-term effects of climate change on water temperatures. Driven by climate-change scenarios, the model forecasts considerable changes throughout the Delta. These changes will affect ecosystem function in a variety of ways. For example, timing of spring spawning temperatures for Delta smelt will shift earlier in the year. Lethal temperatures for Delta smelt will be more frequent in all four climate scenarios.

Our approach has potential weaknesses. While model forecasts appear to predict that Delta smelt are doomed under some climate-change scenarios, the forecasts are spatially limited and do not account for thermal refugia which may exist within the Delta. Additionally, model calibration utilized data collected from 1983 through 2007 and did not sample the same range of temperatures that are likely to be seen in the future. We expect the long-term trend, however, to be small relative to the yearly cycle, and we expect the calculated coefficients to be robust. Flow regimes and water depths in the Delta might be expected to change in the future, as snowmelt arrives earlier and sea level rises. We expect the flow regime to have little effect on the effectiveness of the model; however, it will play a role in setting temperature dynamics over shorter time scales, as it controls the balance between riverine and Bay influences within the Delta.