1 Introduction

Gas flooding in reservoirs is a well-known secondary recovery mechanism and also a gas storage method in the world (Bybee 2001; Azin et al. 2008; Mohammadi et al. 2011; Yuncong et al. 2014; Agrawal et al. 2016; Kumar et al. 2017). Comprehensive analysis of miscible/immiscible gas injection has been undertaken by many researchers using laboratory tests and numerical modeling (Kulkarni and Rao 2005; Alkhazmi et al. 2017; Rezaei et al. 2018). Many aspects of gas injection such as production mechanisms and practical field implementation have also been reviewed (Miri et al. 2014; Agrawal et al. 2016; Kostelnik et al. 2017). Field management and optimization in the gas injection process are important tasks in a reservoir life cycle. Commercial numerical simulators are commonly used for these purposes. Detailed input data including gridding, petrophysics, pressure–temperature–volume (PVT), special core analysis (SCAL), initialization and well data are required for simulation. Comprehensive analysis of reservoir performance, such as well placement optimization and enhanced oil recovery (EOR) scenario prediction, should be performed by numerical methods. However, numerical solution methods based on finite difference or finite element schemes are computationally expensive and time-consuming. Thus, analytical and semi-analytical approaches are necessary for primary analysis for a field development plan. The main advantages of analytical tools are low computational time, simplicity and limited number of input data compared to numerical simulation methods.

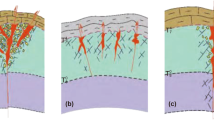
Analytical methods stand between simple tools (the graphical methods and the decline curve analysis) and commercial numerical simulators. CRM is an analytical tool that considers a reservoir as a tank and its formulation is based on the material balance equation between the input (injection rate) and output (production rate) data in a specific control volume (Fig. 1). CRM only requires available and reliable data including production rate, injection rate and producers’ BHP. This method is inspired from electrical engineering in which fluid flow, porous media storativity, pressure depletion and permeability can be conceptually substituted for electric current, capacitance, electric potential and resistance, respectively. The main unknowns in the CRM are interwell connectivity (f) and the time constant (τ). The well production rate in CRM is a function of injection rate, interwell connectivity, time constant and BHP.

Fig. 1
figure 1

CRM as a signal-based method—effect of input signal on output signal in a control volume (Sayarpour 2008)

Full size image

Interwell connectivity is an essential parameter in reservoir management which can affect well rate allocation, infill drilling and sweep efficiency optimization. Interwell connectivity shows the injector contribution in the production of surrounding producers and is a function of reservoir geometry, degree of heterogeneity and well distances. It is also useful for identification of flow barriers as well as high-permeability channels between the injector and the producer (Rafiei 2014). This parameter can be determined using CRM or other direct and indirect methods. Direct methods such as 4D seismic (Huang and Ling 2006; Huseby et al. 2008; Yin et al. 2015, 2016), pulse testing (Dinges and Ogbe 1988; Fokker et al. 2012), interference (Al-Khamis et al. 2005; Ogbe and Brigham 1989; Stewart and Gupta 1984) well tests and tracer tests (Du and Guan 2005; Dugstad et al. 1999; Huseby et al. 2008; Lichtenberger 1991; Refunjol and Lake 1999) are operationally implemented in the field. Although indirect methods are data-driven models and are based on input–output signals which are developed mathematically or statistically, they include artificial neural networks (ANN) (Demiryurek et al. 2008; Panda and Chopra 1998; Artun 2017), wavelet analysis (Jansen and Kelkar 1997), Spearman rank correlation (Heffer et al. 1997; Fedenczuk and Hoffmann 1998; Refunjol and Lake 1999), extended Kalman filter (Liu et al. 2009), pressure-based method (Dinh and Tiab 2008), multiwell productivity method (Valko et al. 2000; Kaviani and Valkó 2010), network model (Gherabati et al. 2017a, b), and streamline simulation (SS) (Batycky et al. 1997, 2005; Thiele et al. 2010; Thiele and Batycky 2006; Baker 2001).

The time constant shows the time needed for transferring the response signal from the injector to the producer (Cao et al. 2014). This parameter is a representative of the fluid storage between injector and producer (Soroush et al. 2014). A low time constant shows a high impact of the injection rate on the production response (Sayarpour et al. 2007). This parameter is a function of total compressibility, productivity index (PI) and pore volume. Generally, a well pair with low interwell connectivity has a large time constant (Cao et al. 2014).

Using historical data, CRM predicts total (oil, gas and water) well production rate. Then, by coupling CRM with oil-cut models such as the Gentil model (Gentil 2005) or the Koval model (Koval 1963), oil, gas and water rates of the well can be estimated.

The main assumptions of the CRM formulation are:

  • Constant PI

  • Constant temperature

  • Low-compressible and immiscible fluids

  • Darcy law flow

  • Constant operational conditions

CRM covers a wide range of applications including reservoir management and optimization, interwell connectivity characterization, heterogeneity identification and rate allocation optimization. Below we present a brief introduction to CRM development, model improvements and its applications.

Mathematical formulation of the CRM was developed by Yousef et al. (Yousef et al. 2006, 2005). To derive this formulation, they coupled the linear productivity model and the material balance equation and defined a connectivity parameter and time constant. Also, they developed a diagnostic tool for identification of flow barriers and transmissibility trends (Yousef et al. 2009). Then, mathematical equations for a system of three control volumes based on tank, producer and injector-producer, using superposition in time, were obtained by Sayarpour et al. (Sayarpour et al. 2007, 2009). Weber et al. (2009) coupled their CRM model with an optimizer and successfully tested the model in a field-scale scenario. Delshad et al. (2009) presented a new application of the CRM in characterization of fractures in the reservoir and quantitatively calculated the fracture permeability. Izgec and Kabir (2010) investigated the capability of the CRM in pre-breakthrough conditions in water flooding and validated the results by streamline simulation. Salazar-Bustamante et al. (2012) combined decline curve analysis and CRM in a carbonate reservoir under gas injection and developed an integrated model, which is applicable in reservoirs under primary depletion and gas injection. Kaviani et al. (2012) introduced the segmented CRM where unknown BHPs change during the interval and compensated CRM in the case of adding a new producer or shutting in an existing producer. Kaviani et al. (2014) performed a comprehensive sensitivity analysis on the impact of different parameters on the CRM performance. They also defined a dimensionless number and with a specific range where CRM is applicable. Mamghaderi and Pourafshary (2013) improved the CRM for layered reservoirs by considering the crossflow between the layers and using available production logging tools (PLT) data. Moreno (2013) developed a multilayer CRM combined with a simple dynamic model and considered variable interwell connectivity, as a function of time, using production and completion data. Moreno and Lake (2014a, b) investigated the impact of noise in the injection rate and designed input signals that improved the information from CRM to estimate interwell connectivity. Also, they studied the uncertainty of interwell connectivity estimations from the CRM. Laochamroonvorapongse et al. (2014) applied CRM for immiscible and miscible water alternating gas (WAG) floods and integrated CRM with other analytical tools such as a Hall plot and the reciprocal of the productivity index for better understanding of reservoir performance. Soroush et al. (2014) studied the effect of change in the producer’s skin factor, drilling new producers and shutting in active existing producers and developed a multiwell compensated capacitance model based on superposition. Cao et al. (2014) presented a two-phase CRM based on the total fluid and oil material balance equations. In addition to pressure changes, they included the saturation variations in the equations and showed that the modified CRM is able to estimate interwell connectivity in all time frames of water flooding. Tao and Bryant (Tao and Bryant 2015) used CRM for gas storage projects to identify connectivity between the extractor and the injector. They showed that CRM is very useful in poorly characterized storage aquifers. Eshraghi et al. (2016) employed CRM for CO2 miscible flooding combined with the Gentil fractional flow model. They further optimized CO2 flooding using heuristic methods such as GA and particle swarm optimization. Mirzayev and Jensen (2016) extended the CRM to a tight reservoir with high well densities and stimulation treatments by dividing the field to some small regions (windows) and considering pseudo wells. Zhang et al. (2017) developed multilayer CRM combined with the ensemble Kalman filter for matching the parameters and performed production optimization by ensemble-based optimization. de Holanda et al. (2018) derived matrix representation of CRM using state space equations and used linear control algorithms for improvement of run-time in large fields. They successfully applied the model in a synthetic reservoir.

Most of the published literature on CRM is concentrated on water flooding projects. There are many gas flooding projects in the world, but comprehensive analysis of CRM performance on gas flooding projects has not been investigated and few published studies exist for gas flooding using the CRM. A list of these studies is provided in Table 1. The objective of this study is to extend the CRM equation in gas flooding systems. It should be noted that the original CRM was used in the studies shown in Table 1 for gas–oil systems. Low-compressible fluids (constant gas density) and linear productivity equation assumptions are not valid in gas flooding systems. In this study, a modified CRM based on compressible fluid consideration (variable density) and the Fetkovich productivity index is developed. To apply these modifications, inputs such as gas density and average reservoir pressure are required. Using this modified CRM, gas flooding projects can be analyzed with an acceptable range of accuracy for total well production rates, interwell parameters and time constants. Then, the model is combined with one empirical fractional flow model to determine well oil and gas rate. Therefore, reservoir management and reservoir performance prediction in gas–oil systems can be performed using the modified CRM and the fractional flow model. Interwell connectivities and well rates are validated using a precise streamline simulator. Statistical error analysis shows that M-CRM results are in good agreement with SS.

Table 1 Researches on the CRM applications in gas flooding
Full size table

2 Modified CRM

The modified CRM (M-CRM) is proposed as an analytical solution in gas–oil systems. The M-CRM is a combination of a modified mass balance equation and a modified productivity equation. There are two approaches for considering gas–oil flow in the reservoir. The first one is based on Cao et al.’s studies (Cao et al. 2014). In this method, saturation changes are imported in the equations, and thus, it is necessary to solve pressure and saturation equations simultaneously. This method is sophisticated and time-consuming when compared to the common CRM. The second one is the Izgec and Kabir approach (Izgec and Kabir 2010), in which they only modified the material balance equation by including density variation in the model. Since the CRM is required to remain simple and fast, we chose the second approach.

Table 2 shows the initial equations of the common CRM and the M-CRM. Mass balance in the common CRM is written for a control volume [Eq. (1)]. Also, the productivity equation can be shown by Eq. (2). The main assumptions for Eqs. (1) and (2) are low-compressible fluid flow and a linear productivity model, respectively. Both assumptions are valid in liquid flow. To use the CRM for gas flooding projects, modifications to previous equations are needed.

Table 2 Common CRM and M-CRM: original and modified mass balance and productivity equations
Full size table

Although the control volume solution is applicable in low-compressible flow, control mass should be used in a compressible condition (gas flooding). Based on density variation versus pressure in the compressible flow, a modified mass balance equation is presented in Eq. (3), where oil and gas densities are imported to the new formulation.

It is safe to assume the linear productivity equation and constant PI in low-compressible flow and pseudo-steady-state conditions. However, in gas–oil systems, the productivity equation is not a linear function and the Fetkovich equation (Fetkovich 1973) is a better option for implementation in gas flooding projects. This formula is shown in Eq. (4) (Yousefi et al. 2019).

In Eqs. (3) and (4), oil can be assumed as a low-compressible fluid, and therefore, \(\frac{{\rho_{\text{o,prod}} }}{{\overline{{\rho_{\text{o}} }} }}\) could be assumed to be equal to 1. The total rate of oil and gas production is given by:

$$q(t) = q_{\text{o}} (t) + \frac{{\rho_{\text{g,prod}} }}{{\overline{{\rho_{\text{g}} }} }}q_{\text{g}} (t)$$
(5)

Therefore, the derivative of rate with respect to time in Eq. (4) is:

$$\frac{{{\text{d}}q(t)}}{{{\text{d}}t}} = J\left( {2\overline{P} \frac{{{\text{d}}\overline{P} }}{{{\text{d}}t}} - 2P_{\text{wf}} \frac{{{\text{d}}P_{\text{wf}} }}{{{\text{d}}t}}} \right)$$
(6)

Combining Eqs. (3) and (6) and replacing the average reservoir pressure with rate yields a first-order ordinary differential equation (ODE):

$$\frac{{{\text{d}}q(t)}}{{{\text{d}}t}} + \frac{1}{\tau }q(t) = \frac{1}{\tau }\frac{{\rho_{\text{g,inj}} }}{{\overline{{\rho_{\text{g}} }} }}i(t) - 2JP_{\text{wf}} \frac{{{\text{d}}P_{\text{wf}} }}{{{\text{d}}t}}$$
(7)

where

$$\tau = \frac{{V_{\text{p}} C_{\text{t}} }}{{2J\overline{P} }}$$
(8)

According to the new equation, there are two fundamental differences between the proposed and previous models, (a) τ is not constant and is a function of average reservoir pressure in each time step (with the unit of day/psi) and (b) density change affects injection rates and consequently, interwell parameters. Thus, the time constant and coefficient of interwell connectivity are affected by the proposed modifications.

The analytical solution of Eq. (7) is as follows:

$$q(t) = q(t_{0} ){\text{e}}^{{\frac{{ - (t - t_{0} )}}{\tau }}} + {\text{e}}^{{\frac{ - t}{\tau }}} \int\limits_{{\xi = t_{0} }}^{\xi = t} {\frac{1}{\tau }\frac{{\rho_{\text{g,inj}} }}{{\overline{{\rho_{\text{g}} }} }}{\text{e}}^{{\frac{\xi }{\tau }}} } i(\xi ){\text{d}}\xi - {\text{e}}^{{\frac{ - t}{\tau }}} \int\limits_{{\xi = t_{0} }}^{\xi = t} {2{\text{e}}^{{\frac{\xi }{\tau }}} J} P_{\text{wf}} \frac{{{\text{d}}P_{\text{wf}} }}{{{\text{d}}\xi }}{\text{d}}\xi$$
(9)

where \(q(t_{0} )\) and \(\xi\) are the initial production rate (bbl/day) and the variable of integration, respectively.

Equation (9) presents a simple solution of M-CRM in the integral form. The right-hand side of this equation shows that the production rate which consists of three terms, namely primary depletion, gas injection effect and BHP changes. According to the equations developed by Sayarpour et al. (Sayarpour et al. 2007, 2009), three different control volumes were developed (Fig. 2). A constant injection rate during each time interval, constant PI and linear BHP drop for producers for the control volumes in the reservoir (the entire reservoir, the producer drainage and the injector–producer pair drainage) and the new formulations by superposition in time are reported in Table 3. Moreover, the objective function for each method is determined.

Fig. 2
figure 2

a CRMT (capacitance–resistance model—tank based) with a single injector and producer in a control volume of a field. b CRMP (capacitance–resistance model—producer based) with one producer and surrounding injectors in a control volume of producer j. c CRMIP (capacitance–resistance model—injector/producer based) in a control volume between each injector/producer pair (Sayarpour 2008)

Full size image
Table 3 Formulations of CRMs based on different control volumes and their objective functions
Full size table

In CRM, fij is the interwell connectivity, which is mathematically defined as:

$$f_{ij} = \frac{{q_{ij} (t)}}{{i_{i} (t)}} \, f_{ij} \ge 0, \, \sum\limits_{i = 1}^{{N_{\text{inj}} }} {f_{ij} \le 1}$$
(13)

where ninj, nprod and nt are the number of producers, injectors and time steps. Subscripts i, j, ij and k refer to injectors, producers, well pair (injector-producer) and time indices, respectively. Subscripts obs and cal represent observed and calculated data, respectively. Also, \(\Delta P_{{{\text{wf}},j}}^{k} = P_{{{\text{wf}},j}}^{k} - P_{{{\text{wf}},j}}^{k - 1}\) and \(\Delta t_{k} = t_{k} - t_{k - 1}\).

3 Workflow

In the current study, a synthetic model is used. Rate and pressure data are generated from numerical simulation and then the M-CRM is used. Reliability of the proposed model in immiscible gas flooding conditions is investigated through the detailed procedure illustrated in Fig. 3. The following procedure is carried out to evaluate the M-CRM’s applicability in gas–oil systems.

Fig. 3
figure 3

A typical flowchart of M-CRM performance in this study

Full size image

Input data including gridding, SCAL, petrophysics, PVT, initialization and well data are required for dynamic modeling. They are imported to the simulator, and the streamline technique is employed for simulation. Subsequently, the results including well allocation factor, well rate and pressure data are acquired. Using historical rate and pressure data of a certain time interval, variation of gas density and average reservoir pressure, the M-CRM is analyzed. Interwell parameters and other unknowns can determined by the optimization algorithm in the history part. To predict the future reservoir performance, M-CRM is used with its own data and its performance is verified by the results of SS. In the following, we briefly describe the procedure steps.

3.1 Streamline simulation

In this section, input data for streamline simulation is imported and a synthetic model is prepared. SS is a numerical simulation technique which uses IMPES formulation (Batycky et al. 1997, 2005; Baker 2001). Phase pressure is solved implicitly in the 3D field and saturations are solved explicitly along 1D streamlines. Thus, this technique is faster than traditional finite difference simulation (Thiele and Batycky 2006; Thiele et al. 2010; Siavashi et al. 2014). The main purpose of using streamline simulation in this study is the capability of SS to calculate well allocation factors for well pairs, which is a validation tool for this work. Consequently, at the end of this step, in addition to the production/injection rate and BHP, allocation factors are determined. The results of M-CRM should be comparable with the results of SS as a reference tool.

3.2 M-CRM

To construct the proposed model, input data including production/injection rate, BHP, average reservoir pressure and also some gas PVT properties for density calculation are required. It should be noted that in a real field, these input data are available and there is no need to run a dynamic model. In this study, inputs are generated from SS and then divided into two sections, history and prediction. A history match is performed by determination of interwell connectivity and total rate and then the prediction scenario is carried out for oil rate estimation.

3.3 Optimization

A genetic algorithm (GA) optimization is used to calculate unknown parameters in M-CRM. GA is a common heuristic optimization method for engineering problems inspired by natural evolution (McCall 2005; Azamipour et al. 2018; Bayat et al. 2011; Chen et al. 2014). There are five steps in GA including initial population, fitness function, selection, crossover and mutation (Emera and Sarma 2005; Ali Ahmadi et al. 2013; Shafiee et al. 2017; Dehghani et al. 2008; Saemi et al. 2007; Chen et al. 2014).

The initial population step is characterized by a set of variables (genes) and a solution (chromosomes). The fitness function evaluates the fitness of each chromosome in the population. The objective of the selection phase is to select the fittest populations to breed a new generation. Crossover is the most significant phase and is the combination of two parents to generate new solutions. Mutation is defined as a small random change in the chromosome, to get a new solution and is used to maintain diversity in the genetic population (McCall 2005).

In this method, first an appropriate range of input data, acceptable initial guesses based on the engineering point of view, and the constraints are selected to avoid local minima and unrealistic results. GA starts from initial guesses and using an iterative procedure, investigates fitness of candidate solutions. In this study, fitness is the objective function. The best answers are stochastically chosen and are modified using crossover and mutation operators. Consequently, highly fit solutions are given more opportunities to reproduce. Finally, once the population has converged to a best answer, the algorithm will be finished (Pencheva et al. 2009). By increasing the number of unknowns in the problem, the complexity of the optimization is increased.

Time constant, interwell parameter, PI and initial rate are determined by a nonlinear optimization technique. In this study, CRMP formulation is employed, and therefore, the number of unknowns in the model is nprod × (ninj + 3). The objective function is to minimize the difference between total production rate obtained by M-CRM and SS as reported in Table 3. The main constraint is Eq. (13) with other parameters equal or greater than zero.

3.4 Validations

Validation of M-CRM performance is performed by SS as a numerical precise simulator. In this study, according to Fig. 3 shows that a validation of the results is carried out in two steps of history and prediction. In the history section, constant interwell parameters, which are determined by GA optimization, should be comparable with the average of well allocation factors obtained from SS for a certain time of analysis. Also, PI(J), which is calculated from M-CRM, should be in the range of PI exported from the commercial simulator. Based on time constant definition, the order of magnitude of τ should be reasonable.

In the prediction section, a validation is performed to compare the oil rate obtained from M-CRM and SS.

Statistical error analysis is performed to compare M-CRM results with that of SS and quantitatively evaluate the model performance. The mean absolute percentage error (MAPE) and the correlation coefficient (CC) are used to verify the results:

$${\text{MAPE}}\,(\% ) = \frac{1}{N}\left( {\sum\limits_{n = 1}^{n = N} {\frac{{\left| {X_{\text{actual}} - X_{\text{estimated}} } \right|}}{{X_{\text{actual}} }}} } \right)$$
(14)
$${\text{CC}} = \, \frac{{\sum {\left( {X_{\text{actual}} - \overline{\text{X}}_{\text{actual}} } \right)} \left( {X_{\text{estimated}} - \overline{X}_{\text{estimated}} } \right)}}{{\sqrt {\sum {\left( {X_{\text{actual}} - \overline{X}_{\text{actual}} } \right)}^{2} \sum {\left( {X_{\text{estimated}} - \overline{X}_{\text{estimated}} } \right)}^{2} } }}$$
(15)

where Xactual is real data, Xestimated is estimated data and N is the number of data points. Low MAPE (%) and CC close to 1 represent reliability of the model.

3.5 Oil-cut models for prediction

The M-CRM is able to calculate the total well production rate in each time step. To predict the oil/gas flow rate, it is necessary to use fractional flow models based on Darcy’s law:

$$\frac{{q_{\text{g}} }}{{q_{\text{o}} }} = \frac{{k_{\text{rg}} }}{{k_{\text{ro}} }}\frac{{\mu_{\text{o}} }}{{\mu_{\text{g}} }} = a{\text{e}}^{{ - {bs}_{\text{g}} }} \frac{{\mu_{\text{o}} }}{{\mu_{\text{g}} }}$$
(16)

where µ is the viscosity (cP); Kr is the relative permeability; and Sg is the gas saturation. The Gentil model as an empirical oil-cut fractional flow model is valid for oil–water systems. In this model, the following equation was developed:

$$\frac{{q_{\text{g}} }}{{q_{\text{o}} }} = \alpha CGI^{\beta }$$
(17)

and therefore:

$$f_{{{\text{o}},jk}} = \frac{{q_{{{\text{o}},jk}} }}{{q_{jk} }} = \frac{1}{{1 + \alpha_{j} {{CGI}}_{jk}^{{\beta_{j} }} }}$$
(18)

where α and β are regression parameters, which can be optimized from production history. CGI is cumulative gas injection (Gentil 2005):

$${CGI}_{jk} = \sum\limits_{k = 1}^{{n_{\text{t}} }} {\sum\limits_{i = 1}^{{n_{\text{inj}} }} {\frac{{\rho_{\text{g,inj}} }}{{\overline{{\rho_{\text{g}} }} }}f_{ij} i_{ij} } }$$
(19)

where α and β are calculated for each producer by optimization. Therefore, with the M-CRM and oil-cut model, the prediction phase can be evaluated.

The reliability of the Gentil model should be verified in a gas flooding scenario. The term \(a\text{e}^{{ - {bs}_{\text{g}} }}\) in Eq. (16) is equivalent to \(\alpha {{CGI}}^{\beta }\). In this study, we investigate the effect of \(\frac{{\mu_{\text{o}} }}{{\mu_{\text{g}} }}\). Both oil and gas viscosities are functions of pressure and increase with an increase in pressure above the bubble point in an identical order of magnitude. Therefore, this term has an insignificant effect on the results and the Gentil model can be used in gas–oil systems.

The aforementioned procedure shows that reservoir management and reservoir performance prediction can be conducted by a combination of the M-CRM and Gentil model. The M-CRM cannot be substituted for commercial reservoir simulators but can be used as a reliable and robust method for simple and quick reservoir performance analysis.

4 Results and discussion

In this section, the proposed model is verified by a synthetic model. Interwell connectivity and oil rates are estimated based on the M-CRM, and the results are compared with SS. In order to evaluate the effect of reservoir parameters on accuracy of the model, sensitivity analysis for drawdown pressure and gas PVT properties is performed.

4.1 Description of the base case

PUNQ-S3 is a benchmark synthetic reservoir model which was extracted from a real field and is owned by the Elf Exploration and Production Company (Juanes et al. 2006; Gu and Oliver 2005). This reservoir is a popular test case for reservoir engineering problems. In this study, the reservoir structure (gridding and geometry) and geological properties are taken from PUNQ-S3. Figure 4 shows a 3D schematic of the model. Also, Fig. 5 demonstrates permeability and porosity maps of the reservoir. The initial reservoir condition is undersaturated with connate water. The model consists of 19 × 28 × 5 grid blocks at a depth of more than 7680 ft. We use this model to analyze the proposed M-CRM performance for an immiscible gas flooding project. Tables 4 and 5 show other reservoir and fluid parameters of the base case, where B is the formation volume factor and µ is the viscosity. Relative permeability curves for oil–water and gas–oil are depicted in Fig. 6.

Fig. 4
figure 4

A 3D schematic and structural map (feet) of the PUNQ-S3 synthetic reservoir model

Full size image
Fig. 5
figure 5

a Porosity (fraction) and b permeability (mD) maps of the base case

Full size image
Table 4 Reservoir parameters of the base case
Full size table
Table 5 Fluid properties of the base case
Full size table
Fig. 6
figure 6

Relative permeability curves for a oil–water and b gas–oil of the base case

Full size image

There are 4 vertical oil producers and 2 vertical gas injectors in the model, and all wells are completed in 5 layers. Production wells are controlled by random oil rates and are limited by minimum BHP, which is 3450 psi. Also, for gas injectors, the gas rate is a target and maximum BHP is the constraint. Production and injection BHPs are maintained above the bubble point pressure (3400.5 psi). Therefore, the source of produced gas is only from gas injectors. Also, the pressure is kept below minimum miscibility pressure to maintain an immiscible displacement.

The simulation is performed for 2520 days to verify the model by the M-CRM. Figure 7 displays the GOR of producers in the model. The new model can be applied in pre-breakthrough and post-breakthrough conditions with acceptable results (Yousefi et al. 2019). In this study, the post-breakthrough condition is chosen for interwell connectivity determination and also to predict oil production rates. Production life is divided into two sections (history and prediction). The history part is used to obtain unknown parameters, and the prediction part is designed to evaluate the performance of the model in the next time steps. 1200 days are selected for the history match and the remaining time (510 days) is used for scenario prediction (Fig. 7). A comparison between the M-CRM and common CRM performance was previously published in a paper by (Yousefi et al. 2019). They showed improvement of using the M-CRM in immiscible gas flooding over the common CRM. In this study, a thorough analysis of the M-CRM is performed in history and prediction parts using sensitivity analysis.

Fig. 7
figure 7

GOR of production wells in history and prediction parts

Full size image

4.2 Analysis of the base case

There are 20 unknowns consisting of fij, τ, Jj and q0 in the model based on the M-CRM. The GA optimization is used for determination of the unknowns. Since there could be numerous solutions in optimization problems, the initial guesses of unknowns are very important. Therefore, the logical input data based on the constraints and nature of this engineering problem guarantees correct answers for unknowns. Table 6 presents optimization results for determination of the unknowns in the PUNQ-S3 model. All parameters are acceptable values regarding the nature of the problem. Interwell parameters (fINJ1−j and fINJ12−j) should be comparable with the average of allocation factors obtained from the SS results.

Table 6 Determination of unknown parameters in M-CRM by GA optimization
Full size table

Table 7 presents interwell connectivity parameters of M-CRM and SS in the history part. Also, the MAPE and CC of the total well production rate are reported in this table. Figure 8 shows the oil production from each well in the prediction part, which is calculated by the Gentil model. The MAPE and CC of the oil rate for all wells are 6.56% and 0.92, respectively. Results indicate the accuracy of the proposed model for interwell parameters calculated as well as the oil rate prediction (Fig. 8).

Table 7 Interwell parameters from SS and M-CRM
Full size table
Fig. 8
figure 8

Well oil production rate in prediction part (510 days)

Full size image

4.3 Sensitivity analysis

According to Eqs. (7) and (8), the proposed model was obtained by applying modifications regarding interwell connectivity and time constant in the common CRM. These modifications were related to the average reservoir pressure and gas properties. Therefore, to show the M-CRM’s capability in all ranges of reservoir conditions, the drawdown pressure (DP) and gas PVT properties are investigated. Other parameters such as permeability, measurement noise, number of measurements, total compressibility and number of producers were investigated by (Kaviani et al. 2014).

4.3.1 Drawdown pressure

Drawdown pressure is an important dynamic parameter in fluid flow through the reservoir especially for gas–oil systems. To investigate its effect on the M-CRM performance, four cases are selected and the PUNQ-S3 model is simulated. All the parameters except the injection rate (the injection pressure) are identical in the four cases. Oil and gas rate controls are chosen for producers and injectors, respectively, and the well BHP is the constraint with 16 unknown parameters. The model performance is investigated for 2700 days. The length of history and prediction sections are 1800 and 900 days, respectively.

Four cases with different injection rates (injection pressure) are selected, and the average drawdown pressures for each case are calculated. Table 8 shows the effect of DP on M-CRM performance in the history and prediction parts. The MAPE and CC for total oil production in the history section and for oil production in the prediction section are also reported. Results show that estimated values are in good agreement with the real data.

Table 8 Effect of drawdown pressure on M-CRM performance
Full size table

The term \(\frac{{\rho_{\text{g,inj}} }}{{\overline{{\rho_{\text{g}} }} }}\) which was added to the new model was developed based on consideration of variations of gas properties with pressure. Thus, this term compensates for the errors which are caused by the common CRM and is applicable in all pressure ranges (Yousefi et al. 2019). Figure 9 presents cross-plots of interwell parameters for the M-CRM and SS in the history section. Figure 10 shows error distribution curves of the predicted oil rate using the Gentil model in the prediction section and relative error percent for predicted rates of 4 producers (120 points). Results show that at all ranges of DP, the reliability of the model for interwell connectivity determination and oil rate prediction is acceptable.

Fig. 9
figure 9

Cross-plots of interwell parameters (M-CRM vs. SS) in the history section—effect of drawdown pressure

Full size image
Fig. 10
figure 10

Error distribution curves of oil rate prediction from M-CRM in the prediction part—effect of drawdown pressure

Full size image

4.3.2 Gas properties

In this section, the effect of PVT properties of injected gas such as viscosity and formation volume factor (density) on the M-CRM performance is investigated. Since oil is a low-compressible fluid, the variation of its properties has negligible impact on the proposed model. In addition to the base case, a lower and a higher viscosity case and a lower and higher gas formation volume factor (FVF) are assumed (Fig. 11). All properties except gas viscosity and FVF are identical for the five cases. Time intervals between 2220 and 5460 days (3270 days) are considered for model performance analysis, 2160 days for the history part and 1110 days for the prediction part.

Fig. 11
figure 11

Base case, higher and lower cases for a viscosity and b gas FVF

Full size image

Table 9 reports the effect of gas viscosity and FVF on the M-CRM performance in the history and prediction periods in the PUNQ-S3 model. The MAPE in history and prediction sections are both below 5% and 10%, respectively, which show the strength of the M-CRM in a wide range of gas PVT properties. Also, CCs have quite an acceptable range (close to 1).

Table 9 Effect of gas PVT properties on the M-CRM performance
Full size table

Figure 12 displays cross-plots of interwell parameters in the history section for different gas properties. Results show that the proposed model correctly predicts interwell parameters in various operational conditions. Additionally, gas viscosity and FVF do not have negative effects on the results. The error distribution curves of estimated oil rate in the prediction section are demonstrated in Fig. 13. Although the Gentil model tends to underpredict the oil rate in many data points, generally the results are acceptable and reflect suitable performance of the M-CRM.

Fig. 12
figure 12

Cross-plots of interwell parameters (M-CRM vs. SS) in the history section—effect of gas properties

Full size image
Fig. 13
figure 13

Error distribution curves of oil rate prediction form the M-CRM in the prediction part—effect of gas properties

Full size image

It is noted that more reliable results for the total rate in the history period and the oil rate in the prediction period are obtained when high gas viscosity and low gas FVF are incorporated for the injected gas. This behavior is a result of gas deviation from the ideal behavior in low viscosity and high FVF conditions. Thus, in these conditions, the M-CRM performance leads to high errors.

5 Conclusions

This study presented a new formulation for CRM (M-CRM) as a simple tool for reservoir performance analysis and prediction in immiscible gas flooding projects. New modifications using gas density variation and average reservoir pressure affected interwell connectivity parameters and time constants in the proposed model. A combination of the M-CRM and the Gentil model was employed for a comprehensive analysis of the PUNQ-S3 synthetic model in history and prediction sections. From the results of this study, we concluded that:

  • A detailed flowchart for M-CRM performance evaluation in history-matching and future reservoir performance prediction in immiscible gas flooding was introduced. Furthermore, we used streamline simulation for validation of the results and a genetic algorithm for optimizing unknown parameters.

  • The M-CRM was performed on a synthetic reservoir model under immiscible gas flooding. The total production rates of wells and interwell parameters in the history part and oil production rates in the prediction part were estimated with an acceptable relative error (below 10%) and a correlation coefficient (close to 1).

  • By considering a variable gas density with pressure, the high drawdown pressure did not have a negative impact on the validity of the M-CRM and Gentil model.

  • Gas PVT properties such as viscosity and FVF did not affect the M-CRM robustness in the immiscible gas flooding process. Although employing low gas viscosity and high gas FVF resulted in relatively high errors, the M-CRM performance is acceptable.