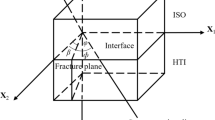
Abstract
Fracture systems in nature are complicated. Normally vertical fractures develop in an isotropic background. However, the presence of horizontal fine layering or horizontal fractures in reservoirs makes the vertical fractures develop in a VTI (a transversely isotropic media with a vertical symmetry axis) background. In this case, reservoirs can be described better by using an orthorhombic medium instead of a traditional HTI (a transversely isotropic media with a horizontal symmetry axis) medium. In this paper, we focus on the fracture prediction study within an orthorhombic medium for oil-bearing reservoirs. Firstly, we simplify the reflection coefficient approximation in an orthorhombic medium. Secondly, the impact of horizontal fracturing on the reflection coefficient approximation is analyzed theoretically. Then based on that approximation, we compare and analyze the relative impact of vertical fracturing, horizontal fracturing and fluid indicative factor on traditional ellipse fitting results and the scaled B attributes. We find that scaled B attributes are more sensitive to vertical fractures, so scaled B attributes are proposed to predict vertical fractures. Finally, a test is developed to predict the fracture development intensity of an oil-bearing reservoir. The fracture development observed in cores is used to validate the study method. The findings of both theoretical analyses and practical application reveal that compared with traditional methods, this new approach has improved the prediction of fracture development intensity in oil-bearing reservoirs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fractures are regarded as facilitating both migration and emplacement of oil and gas within reservoir rocks, and fracture assessment is one of the most critical issues in reservoir evaluation. Prediction and identification of fractures mainly involve post-stack geometric attributes analysis and related techniques dependent on the development of seismic anisotropies. Analysis of geometric attributes derived from post-stack seismic information is a mature discipline, and attributes such as amplitude, coherence and curvature are mainly used to describe faults and indirectly delineate belts of fracture system development. When considering micro-fractures smaller than the longitudinal resolution of the seismic wavelet, although individual fractures cannot be identified, their gross effect on reflection amplitude information can be applied to predict fracture properties, based on the theory of equivalent anisotropic media. Currently, common equivalent media theories include the Hudson (1980, 1981) model and linear-slip theory (Schoenberg 1980, 1983), and T-matrix theory that explicitly takes into account fracture interactions (Jakobsen et al. 2003; Zhao et al. 2016). These theories can describe a cluster of vertically and high-angle aligned fractures as an HTI medium. According to a P-wave reflection coefficient approximation in the HTI medium, the inversion of azimuth and azimuthal anisotropy is performed, seeking to solve for fracture direction and intensity (Ruger 1998; Schoenberg and Sayers 1995; Yin and Yang 1998; Bakulin et al. 2000; Zhu et al. 2001; Hall and Kendall 2003). In addition, fracture direction and fracture density can be estimated through the observed ellipse phenomenon of amplitude varying with azimuth (Liu and Dong 1999; Luo and Evans 2004; Yang et al. 1998). However, reservoirs may not only have high-angle fractures but also have low-angle fractures or horizontal fine layering background. Since the presence of horizontal fractures leads to a physically significant change of P-wave AVAZ (amplitude versus incident angle and azimuth) attributes including reflectivity intercept, gradient and anisotropic terms, application of the inversion method for conventional HTI medium AVAZ attributes is not appropriate for fracture prediction in orthorhombic media. The amplitude ellipse fitting method is affected by horizontal fractures and fluid properties so as to lower the accuracy of vertical fracture prediction. This means that predictive approaches to AVAZ based on an orthorhombic medium need to be modified to increase the accuracy of fracture prediction.
Forward modeling of the seismic elastic wave field through an orthorhombic medium has been investigated (Shao et al. 1998; Fu 2001; Fu and He 2001; Daley and Krebes 2006). Lu et al. (2005) and Faranak et al. (2014) conducted research on Thomsen anisotropic parameters inversion using P-wave travel time in an orthorhombic medium. However, investigation of AVAZ fracture prediction methods for an orthorhombic medium is still conceptual. Bachrach et al. (2009) expands the approximation for reflection coefficient from an HTI medium to an orthorhombic medium based on the study of Pšenčík and Vavryčuk (1998, 2001) and uses wide-azimuthal pre-stack seismic data from the American Bakken Shale to develop AVAZ attributes inversion based on an orthorhombic medium. Far et al. (2013, 2014) derived a complicated reflection coefficient expression of anisotropic media and inverse elastic parameters by imposing singular value decomposition on numerical simulation results based on prior information such as isotropic background. Systematic theoretical analysis is lacking regarding the relationship between orthorhombic media AVAZ attributes and fracture nature, and AVAZ attributes in orthorhombic media appear to have little practical application. Therefore, investigation of fracture prediction based on an orthorhombic medium is fundamental and forward-looking work and indicates the trend of future fracture prediction studies.
The approximate formula for reflection coefficient in an orthorhombic medium is simplified in this paper. This is the first time that the effect of vertical fractures and fluid indicative factors on the prediction result of fracture intensity by AVAZ attributes within an orthorhombic medium is discussed. A new approach to predicting fracture intensity in an orthorhombic medium for oil-bearing fractured reservoirs is established. The superiority of this new method is discussed in theory and testified by a case study in a fractured oil reservoir.
2 Theory
Linear-slip theory considers that a fracture is a uniquely thin layer surrounded by two-dimensional infinite faces. In other words, a fracture is regarded as a plane without thickness under ideal conditions, and the shape and microstructure of a fracture are ignored. Suppose that the stress across a fracture is quite high, ten times larger across it compared to undisturbed rocks around a fracture; suppose that there is a linear relationship between displacement across a fracture plane and stresses on a fracture plane; and suppose that displacement across a fracture plane is discontinuous, without a change to rotation.
The equivalent compliance matrix of a fractured medium may be expressed as a background compliance matrix sb and a fracture compliance matrix sf, in accordance with linear-slip theory focusing on horizontally isotropic media (Schoenberg 1980, 1983).
If background is a VTI medium, then the elastic matrix is:
c12b = c11b − 2c66b. Matrix sf is a group of fracture compliances with the x1-axis defined as the normal direction, which can be expressed as:
KN is the normal fracture compliance, and KV and KH are two transverse compliances in the vertical and horizontal directions, respectively. KV ≠ KH, the above equation is orthorhombic.
Schoenberg and Helbig (1997) introduce dimensionless weakness parameters to replace KN, KV and KH, enabling a more convenient calculation:
Then, the fracture compliance matrix is changed to:
∆N, ∆V, ∆H are, respectively, the normal weakness, vertical weakness and horizontal weakness caused by fractures. Weakness ranges from 0 to 1, and 0 denotes a medium without anisotropy. cb and sf are added into c, which implies the insertion of a group of vertical fractures into the VTI background, and then, the elastic parameter matrix within the orthorhombic medium is expressed as:
Specifically:
And 0 is a 3 × 3 order 0 matrix.
3 Reflection coefficient approximation in an orthorhombic medium
Bachrach et al. (2009) expands the approximation of a reflection coefficient in an HTI medium to arrive at the approximation in an orthorhombic anisotropic medium based on the study by Pšenčík and Martins (2001):
Specifically, α and β are P-wave velocity and S-wave velocity in an isotropic background medium. θ is incident angle, φ is the azimuth in the natural system of coordinates, while φ = φs − φsym. φs is the azimuth of an observed line deviating from the coordinate system and φsym is the azimuth of the symmetry axis away from the coordinate system. IP is the P-wave impedance. G is the shear modulus. The symbol on top
 is an average value of the medium physical properties of two layers surrounding the reflecting interface. The prefix symbol “Δ” is the difference between physical properties of two layers surrounding the reflecting interface. ɛx, ɛy, γx, γy, δx, δy and δz are anisotropic parameters, which are defined by \({\ A}_{ij}\), which is the density normalized stiffness of the OA (orthorhombic anisotropy) medium, P-wave velocity and S-wave velocity of the background medium.
is an average value of the medium physical properties of two layers surrounding the reflecting interface. The prefix symbol “Δ” is the difference between physical properties of two layers surrounding the reflecting interface. ɛx, ɛy, γx, γy, δx, δy and δz are anisotropic parameters, which are defined by \({\ A}_{ij}\), which is the density normalized stiffness of the OA (orthorhombic anisotropy) medium, P-wave velocity and S-wave velocity of the background medium.
Normally, to simplify the reflection coefficient expression in an AVO study, the effect of higher-order terms of incidence angle is neglected, and thus, P-wave reflection coefficient in an orthorhombic medium can be simplified:
Nevertheless, the assumptions used to derive Eq. (23) reduce some calculation accuracy, regardless of its accessibility to inversion approaches. To obtain an approximation that is easy to invert while ensuring its calculation accuracy, Eq. (11) may be modified to Eq. (24) in terms of azimuth effect in this paper,
where
Two-term approximations of P-wave reflection coefficient neglect higher-order both azimuth and incident angle terms:
The model comprising of two layers of isotropic background is established (as indicated in Table 1); then, the upper layer is converted to an orthorhombic medium. Horizontal fractures with tangential compliance ZT of 5 × 10−12 m/Pa and vertical fractures with vertical compliance KV of 2 × 10−11 m/Pa are emplaced into the upper isotropic background, while the tangential weakness of horizontal fractures is 0.0441 and the vertical weakness of vertical fractures is 0.1434. The ratio between fracture normal compliance and tangential (vertical) compliance indicates the fracture fluid property. If this value is between 0 and 0.2, fractures are considered to be mainly filled with liquid. When fluid indicative factor is 0, fractures are considered to be full of liquid, and as the fluid property indicative factor increases, the liquid content in fluid drops. Fixing the fracture fluid property indicative parameter is 0.1, the fracture filling with oil in an orthorhombic medium is simulated. Figure 1a shows the azimuthal reflection response character of the model based on the three-term expression (Eq. 11) and the two-term approximation approach (Eq. 23) with the higher-order term related to incidence angle removed, and Fig. 1b shows the relative error between them. Figure 2a displays the azimuthal reflection response character of the model based on the three-term expression (Eq. 11) and the two-term approximation approach (Eq. 28) with higher-order term relating to azimuth removed, and Fig. 2b displays their relative errors. As indicated in Figs. 1 and 2, as the incident angle goes up, the effect of azimuth on reflection increases; the error obtained from Eq. (23) decreases with the increase in azimuth, while azimuth ranges from 0° to 90°, and the error obtained from Eq. (28) increases with the increasing azimuth under the same conditions. Reflection coefficient accuracy obtained from Eq. (28) is higher than that obtained from Eq. (23). For instance, when the angle of incidence is 30°, the error from Eq. (23) is about 10%, but the error from Eq. (28) is under 2%. Therefore, Eq. (28) possesses the advantages of easy inversion and higher computational accuracy.
A simplified approximation of reflection coefficient calculated by Eq. (23) (a) and its error (b)
A simplified approximation of reflection coefficient calculated by Eq. (28) (a) and its error (b)
4 Reflection attributes in an orthorhombic medium
The properties of vertical fractures in the model discussed above remain unchanged, and Figs. 3 and 4 show the reflection coefficient of an OA medium in which fracture filling with liquid fluid varies with incident angle calculated by Eq. (28), while the horizontal fracture compliances are changing. With the increase in incident angle, the effect of horizontal fractures on the reflection coefficient goes up. As horizontal fracture intensity rises, the azimuthal reflective difference gets increasingly smaller. As a result, the method of using azimuthal reflection variation to predict vertical fracture density may have a lower accuracy due to the presence of horizontal fractures.
When the equivalent HTI medium of vertical fractures is considered, the reflection coefficient shows elliptical properties under azimuthal polar coordinates, and the ratio of long axis to short axis in that ellipse is related to the fracture intensity. The stiffness \({c}_{{44{\text{b}}}}\) of the VTI media in Eq. (2) can be obtained by \({c}_{{44{\text{ - iso}}}} - \mu \Delta T\). Here, \({c}_{{44{\text{ - iso}}}}\) is the host isotropic rock stiffness and μ is the Lamé constant. ΔT has the physical meaning of the tangential weakness added by the horizontal fractures to the host isotropic rock. ΔV defined by Eq. (4) has the physical meaning of the vertical weakness added by the vertical fractures to VTI background. ΔT and ΔV indicate horizontal and vertical fracture intensities, respectively. As indicated in Figs. 5a and 6a, the ellipse ratio is not only affected by vertical fractures, but also impacted by the weakness of horizontal fractures and the fluid property indicative factor of both horizontal and vertical fractures. The effect of fluid property is higher than the weakness of horizontal fractures. As a result, although the method of ellipse fitting reflects the development of vertical fractures, the increase in horizontal fractures and fluid property indicative factor may decrease prediction accuracy. \(B_{\text{ani}}\) is divided by the reflection coefficient at 0° incident angle in Eq. (22), and the result is defined as scaled B. We analyze with the assumption that the fracture fluid indicator range is 0–0.2 which means fractures are mainly filled with fluid. From Figs. 5b and 6b, scaled B attributes are mainly affected by the degree of development of vertical fracturing, and the scaled B attributes become larger with increasing development of vertical fracturing. The effect of the fluid indicative factor on scaled B attributes is higher than that of horizontal fracturing. From examination of the contrast between Figs. 5 and 6, the decreasing of the fracture prediction accuracy by using scaled B attributes affected by horizontal fractures and fluid property indicative factor is lower than the one by using the ellipse ratio. The ability of scaled B attributes on weakening the influence of horizontal fractures is higher than weakening the influence of fluid property on vertical fracture prediction. Therefore, compared to conventional approaches, the scaled B attributes approach better reflects the development of vertical fractures in an oil reservoir with developed horizontal fractures.
5 Case study
The Binchang block, located in the overlapping area of the Yishan slope of the Ordos Basin and Weibei uplift, was selected as the target area for this case study. The eighth interval of the Yanchang Formation was chosen as the target layer. Erosion surfaces, tabular bedding, trough bedding and sand streak bedding were observed in cored sections of the reservoir. The overall profile showed an upward-coarsening sequence, which was the result of delta front deposition of underwater distributary channels. The development of faulting and fracturing played an important role in the migration and accumulation of oil and gas and was critical to achieving high oil and gas production rates. The types of reservoir porosity include intergranular pores and intragranular dissolved pores. According to results of fracturing inclination measurements, low-angle fractures account for almost 20% of the total volume, while inclined fractures make up 30% or so. High-angle vertical fractures account for approximately 50% of the observed fracturing. Part of fracture common interface is oil accumulation, or oil migration from fracture interface to reservoir bedding. In Fig. 7, bedding and fracturing can be seen in a core from the Chang 8 Formation. Therefore, reflection coefficient approximations based on an orthorhombic medium could better reflect the actual situation in this case than the approximations based on a conventional HTI medium. Figure 8 shows the gather data after seismic processing, and the red line represents the position of the target layer. The gathered data for inversion have six different azimuths, and the maximum incident angle is about 35°. The data meet the requirements of AVAZ analysis.
Figure 9 shows fracture prediction results from a conventional method which assumed stratum approximated to an HTI medium, and Fig. 10 shows fracture prediction results using the new method introduced in this paper which assumes that the reservoir resembles an orthorhombic medium. In the two pictures, the more the fractures developed the warmer the color tones used to represent them. Several faults distributed northeast were observed. Figures 9 and 10 both show evidence of fracture zones developing alongside the faults. In the pictures, the positions of the wells developed with fractures are marked with circles or triangles, and photographs of the reservoir rock core are shown. In Figs. 9 and 10, wells represented by purple triangles are all positioned in areas of cool color tone, namely where few fractures were predicted. Core observation, however, showed extensive horizontal fracture development within the wells. Therefore, the development of horizontal fractures can be seen to decrease fracture prediction accuracy. Well positions marked with black circles matched fracture development prediction results shown in Figs. 9 and 10 well. Wells marked with blue circles in Fig. 9 were situated in an area represented by a cold color tone indicating a low fracture intensity; this conflicted with the actual observations. However, in Fig. 10, these points are located in the fracture high development area represented by warm color tones. The locations of wells with development of horizontal fractures represented by blue circles were confirmed by core observations, proving that the presence of horizontal fractures decreases fracture prediction results when modeling the reservoir as an HTI medium. Compared with Fig. 9, Fig. 10 shows a better fracture prediction result, which is in better agreement with the observation in wells. Since the effect of horizontal fractures on fracture prediction result based on the equivalent orthorhombic medium was lower than the effect based on an equivalent HTI medium, this method of modeling reflection coefficient within an orthorhombic medium using AVAZ attributes for fracture prediction gave improved results.
6 Conclusions
In this paper, a reflection coefficient approximation within an orthorhombic medium is simplified to extract AVAZ attributes sensitive to fracturing. It was seen that two-term approximate reflection coefficient expressions within an orthorhombic medium with the higher-order azimuthal term removed have a higher accuracy than that with the higher-order incident angle term removed. The presence of horizontal fractures may decrease azimuthal difference in reflection coefficient within an orthorhombic medium, therefore decreasing the prediction accuracy of vertical fracture intensity. Theoretical analysis suggests that, when the fracture fluid is mainly filled with liquid, even though the presence of horizontal fractures and fluid indicative factor decreases the accuracy of the scaled B attributes in fracture prediction, its impact on the scaled B attributes is nevertheless lower than that seen using an ellipse fitting result. The application to an oil reservoir proves that the method of using the scaled B attributes to predict fracture intensity can better reflect realistic geological situations than conventional fracture prediction approaches. Both theoretical analysis and the case study result indicate that for oil-bearing reservoirs with simultaneous development of horizontal and vertical fractures, the new approach introduced by this paper has a better accuracy of fracture prediction than conventional methods. Whereas this study focuses on fracture prediction based on AVAZ attributes for an oil-bearing reservoir, fracture prediction in an orthorhombic medium filled with gas needs further analysis. Still, for more complicated fractured models, the assumption that the reservoir is equivalent to an orthorhombic medium may break down, and most of our developments will need to be revised.
References
Bachrach R, Sengupta M, Salama A, et al. Reconstruction of the layer anisotropic elastic parameter and high-resolution fracture characterization from P-wave data: a case study using seismic inversion and Bayesian rock physics parameter estimation. Geophys Prospect. 2009;57:253–62. https://doi.org/10.1111/j.1365-2478.2008.00768.x.
Bakulin A, Grechka V, Tsvankin I. Estimating of fracture parameters from reflection seismic data-Part II: fractured models with orthorhombic symmetry. Geophysics. 2000;65:1803–17. https://doi.org/10.1190/1.1444864.
Daley PF, Krebes ES. Quasi-compressional group velocity approximation in a weakly anisotropic orthorhombic medium. Journal of Seismic Exploration. 2006;14:319–34.
Far ME, Sayers CM, Thomsen L, et al. Seismic characterization of naturally fractured reservoirs using amplitude versus offset and azimuth analysis. Geophys Prospect. 2013;61:427–47. https://doi.org/10.1111/1365-2478.12011.
Far ME, Hardage B, Wagner D. Fracture parameter inversion for Marcellus Shale. Geophysics. 2014;79:C55–66. https://doi.org/10.1190/geo2013-0236.1.
Faranak M, Margrave GF, Daley PF. Estimation of elastic stiffness coefficients of an orthorhombic physical model using group velocity analysis on transmission data. Geophysics. 2014;79:27–39. https://doi.org/10.1190/geo2013-0203.1.
Fu D. Elastic wavefield forward modeling with pseudo-spectral method in orthorhombic anisotropy media. Geophysical Prospecting for Pet. 2001;40(3):8–14 (in Chinese).
Fu DD, He QD. Elastic wavefield forward modeling with pseudo-spectral method in orthorhombic anisotropy media. Geophysical Prospecting for Petroleum. 2001;40(3):8–14 (in Chinese).
Hall S, Kendall JM. Fracture characterization at Valhall: application of P-wave amplitude variation with offset and azimuth (AVOA) analysis to a 3D ocean-bottom data set. Geophysics. 2003;68:1150–60. https://doi.org/10.1190/1.1598107.
Hudson JA. Overall properties of a cracked solid. Proc Camb Phil Soc. 1980;88(2):371–84. https://doi.org/10.1017/S0305004100057674.
Hudson JA. Wave speeds and attenuation of elastic waves in material containing cracks. Geophys J Int. 1981;64(1):133–55. https://doi.org/10.1111/j.1365-246X.1981.tb02662.x.
Jakobsen M, Hudson JA, Johansen TA. T-Matrix approach to shale acoustics. Geophys J Int. 2003;154:533–58. https://doi.org/10.1046/j.1365-246X.2003.01977.x.
Liu Y, Dong MY. Azimuthal AVO in anisotropic medium. Oil Geophysical Prospecting. 1999;34(3):260–7 (in Chinese).
Lu MH, Tang JH, Yang HZ, et al. P-wave traveltime analysis and Thomsen parameters inversion in orthorhombic media. Chinese Journal of Geophysics. 2005;48(5):1167–71 (in Chinese).
Luo M, Evans BJ. An amplitude-based multiazimuth approach to mapping fractures using P-wave 3D seismic data. Geophysics. 2004;69:690–8. https://doi.org/10.1190/1.1759455.
Pšenčík I, Vavryčuk V. Weak contrast PP wave displacement R/T coefficients in weakly anisotropic elastic media. Pure appl Geophys. 1998;151:699–718. https://doi.org/10.1007/s000240050137.
Pšenčík I, Martins JL. Properties of weak contrast PP reflection/transmission coefficients for weakly anisotropic elastic media. Stud Geophys Geod. 2001;45:176–99. https://doi.org/10.1023/A:1021868328668.
Ruger A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media. Geophysics. 1998;63:935–47. https://doi.org/10.1190/1.1444405.
Shao ZL, He ZH, Huang DJ. Finite difference numerical modeling of seismic records in the orthotropic medium. Computing techniques for geophysical and Geochemical Exploration. 1998;20(4):300–5 (in Chinese).
Schoenberg M. Elastic wave behavior across linear slip interfaces. J Acoust Soc Am. 1980;68:1516–21. https://doi.org/10.1121/1.385077.
Schoenberg M. Reflection of elastic waves from periodically stratified media with interfacial slip. Geophys Prospect. 1983;31:265–92. https://doi.org/10.1111/j.1365-2478.1983.tb01054.x.
Schoenberg M, Helbig K. Orthorhombic media: modeling elastic wave behavior in a vertically fractured earth. Geophysics. 1997;62(6):1954-74. https://doi.org/10.1190/1.1444297.
Schoenberg M, Sayers C. Seismic anisotropy of fractured rock. Geophysics. 1995;60:204–11. https://doi.org/10.1190/1.1443748).
Yang X, Wang ZL, Yu YY. The overview of seismic techniques in prediction of fracture reservoir. Progress in Geophysics. 1998;20(4):300–5 (in Chinese).
Yin K, Yang HZ. AVO in anisotropic media. Chinese Journal of Geophysics. 1998;41(3):382–91 (in Chinese).
Zhao L, Yao Q, Han D, Yan F, Nasser M. Characterizing the effect of elastic interactions on the effective elastic properties of porous, cracked rocks. Geophys Prospect. 2016;64:157–69. https://doi.org/10.1111/1365-2478.12243.
Zhu PM, Wang JY, Yu WH, et al. Inverting reservoir fracture density using P-wave AVO data. Geophysical Prospecting for Petroleum. 2001;40(2):1–12 (in Chinese).
Acknowledgements
This study was financially supported by 973 Program (No. 2014CB239104), NSFC and Sinopec Joint Key Project (U1663207) and National Key Science and Technology Project (2017ZX05049002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Edited by Jie Hao
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, YW., Liu, XW., Lu, YX. et al. Fracture prediction approach for oil-bearing reservoirs based on AVAZ attributes in an orthorhombic medium. Pet. Sci. 15, 510–520 (2018). https://doi.org/10.1007/s12182-018-0250-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12182-018-0250-1