1 Introduction

In situ stresses are generated or controlled by a series of geological events such as sedimentation and tectonic movements. Far-field stresses imposed on the basin boundary are transferred across the basin (Luo and Dusseault 1998). Three orthogonal in situ stresses are normally assumed for the convenience of description and study: vertical stress (\(\sigma_{\text{V}}\)), maximum horizontal stress (\(\sigma_{\text{H}}\)), and minimum horizontal stress (\(\sigma_{\text{h}}\)). Generally, three stress regimes are defined according to the relative magnitude of the three principal stresses: normal faulting stress regime (\(\sigma_{\text{V}} > \sigma_{\text{H}} > \sigma_{\text{h}}\)), strike-slip faulting stress regime (\(\sigma_{\text{H}} > \sigma_{\text{V}} > \sigma_{\text{h}}\)), and thrust faulting stress regime (\(\sigma_{\text{H}} > \sigma_{\text{h}} > \sigma_{\text{V}}\)) (Anderson 1905). In situ stresses vary due to some changes in the environment. For example, during drilling of a circular hole, stresses will redistribute around the hole, which are described by the Kirsch equation (Kirsch 1898). In an oilfield subjected to injection or production activities, stresses vary due to volumetric strain changes. This has been found in conventional resource reservoir deformation and casing stability analysis (Geertsma 1973; Safai and Pinder 1980; Segall and Fitzgerald 1998; Du and Olson 2001; Soltanzadeh and Hawkes 2008; Han and Dusseault 2008), caprock integrity analysis (Han et al. 2012; Rahmati et al. 2014), and completion of unconventional resources (Nagel et al. 2013; Han et al. 2014). In petroleum engineering, especially in development of unconventional resources, effective determination of in situ stress is critical to ensure successful drilling, quality completion, and reservoir containment analysis.

Vertical in situ stress is usually assumed to be equal to the weight of the overlying layers per unit area and can be computed by integrating the bulk density log data. The direction of maximum or minimum horizontal in situ stress can either be observed from image logs or caliper logs, or be estimated from basin-scale observation of geological events. The magnitude of minimum in situ stress can be measured by leak-off tests (LOT) or hydraulic fracturing tests (Haimson and Fairhurst 1967; Haimson 1974). Small-scale hydraulic fracturing tests are called mini-frac tests. There are many types of mini-frac tests, such as Halliburton’s Diagnostic Fracture Injection Test (DFIT) and Schlumberger’s Modular Formation Dynamics Tester (MDT). However, there is no tool for direct measurement of maximum horizontal in situ stress. The determination of maximum horizontal in situ stress magnitude is often achieved by calculation from borehole breakouts, minimum horizontal stress, and rock mechanical properties such as cohesion, friction angle, and unconfined compressive strength (UCS) (Zoback et al. 1985; Peška and Zoback 1995). There are many other studies of in situ stress determination. Ervin and Bell used breakdown pressure or leak-off pressure from formation leak-off tests to calculate the maximum horizontal stress estimation (Ervin and Bell 1987). Cornet and Valette (1984) developed a method based on normal stress measurements and fast flow rate reopening tests to calculate in situ stresses. Aadnoy (1990) developed a method to determine direction and magnitudes of horizontal in situ stresses based on the formation breakdown pressure of a circular borehole of arbitrary trajectory. The method has been successfully applied to a set of North Sea data. All the available methods for maximum horizontal stress calculation are based on a circular borehole shape. There are currently no reports found on the calculation of in situ stresses from elliptical boreholes.

In most basins, the scenario of perfect circular boreholes is not common. The drilled boreholes have some degree of elliptical geometry rather than circular geometry due to factors of borehole elastic deformation and/or breakouts. It is therefore necessary to investigate in situ stress inversion from a borehole of elliptical geometry and to compare the difference between the results of elliptical borehole-based inversion and circular borehole-based inversion. To this end, we developed an inversion technique to calculate in situ stress based on the information of borehole mud pressure that created drilling-induced fracture for any elliptical borehole of arbitrary well trajectory.

In the following sections, the theory of the proposed approach is introduced, and case studies are demonstrated from the Appalachian Basin. The results indicate that even a small amount of borehole ellipticity has considerable influence on the magnitude of estimated horizontal in situ stresses.

2 Mathematical model

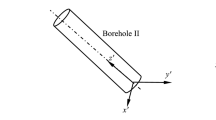
To develop stress equations around elliptical boreholes, we started with a circular borehole assumption. For an arbitrary well trajectory with a given inclination and azimuth as shown in Fig. 1, the two stresses normal to the circular well bore can be written as:

$$\sigma_{x} = \{ \sigma_{\text{H}} \cos^{2} (\phi - \beta ) + \sigma_{\text{h}} \sin^{2} (\phi - \beta )\} \cos^{2} \gamma + \sigma_{\text{v}} \sin^{2} \gamma$$
(1)
$$\sigma_{y} = \sigma_{\text{H}} \sin^{2} (\phi - \beta ) + \sigma_{\text{h}} \cos^{2} (\phi - \beta )$$
(2)

where \(\sigma_{x}\) and \(\sigma_{y}\) are two orthogonal stresses along the cross section of the arbitrary well trajectory (\(\sigma_{x}\) is the normal in situ stress in the x direction; \(\sigma_{y}\) is the normal in situ stress in the y direction); \(\sigma_{\text{v}}\) is the vertical stress; \(\sigma_{\text{H}}\) is the maximum horizontal stress; \(\sigma_{\text{h}}\) is the minimum horizontal stress; γ is the borehole inclination; \(\phi\) is the borehole azimuth; β is the angle between \(\sigma_{\text{H}}\) and the north.

Fig. 1
figure 1

Sketch map showing well geometry, coordination system, and in situ stress directions

Full size image

Suppose \(\sigma_{x}\) > \(\sigma_{y}\), the fracture pressure of a circular borehole can be derived from the Kirsch equations.

$$P_{\text{f}} = P_{\text{w}} = 3\sigma_{y} - \sigma_{x} - P_{\text{p}} + T_{0}$$
(3)

where Pp is the pore pressure; T0 is the rock tensile strength; Pf is the borehole pressure at fracture; Pw is the borehole pressure.

For an arbitrary borehole, \(\sigma_{x}\) is not necessarily always greater than \(\sigma_{y}\), if \(\sigma_{x}\) < \(\sigma_{y}\), the fracture pressure of a circular borehole becomes:

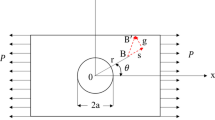
$$P_{\text{f}} = P_{\text{w}} = 3\sigma_{x} - \sigma_{y} - P_{\text{p}} + T_{0}$$
(4)

However, in real drilling practice, even when a borehole is drilled as a circular hole, elliptical boreholes are often observed because of the heterogeneous stress concentration around the borehole. This will happen as either a deformation of the borehole or as wellbore breakouts. Lekhnitskii (1968) investigated the tangential stresses on the short or long axis of the elliptical hole in plates under tension. Similarly, the elliptical borehole geometry under compression is illustrated in Fig. 2. The two orthogonal compression stresses \(\sigma_{x}\) and \(\sigma_{y}\) apply along the cross section of an inclined wellbore. By adapting the work of Lekhnitskii, the tangential stresses at the short or long axis of the elliptical hole under compression can be written as Eqs. (5) or (6) in the case of \(\sigma_{x}\) > \(\sigma_{y}\).

$$\sigma_{B} = (2c + 1)\sigma_{y} - \sigma_{x} - (2c - 1)P_{\text{w}}$$
(5)
$$\sigma_{A} = (2/c + 1)\sigma_{x} - \sigma_{y} - (2/c - 1)P_{\text{w}}$$
(6)
Fig. 2
figure 2

Cross sections of elliptical borehole under the two orthogonal compression stresses \(\sigma_{x} \,\, {\text{and}}\,\,\sigma_{y}\). a \(\sigma_{x} > \sigma_{y}\), b \(\sigma_{x} < \sigma_{y}\)

Full size image

In the case of \(\sigma_{x}\) < \(\sigma_{y}\), the two equations become:

$$\sigma_{B} = (2c + 1)\sigma_{x} - \sigma_{y} - (2c - 1)P_{\text{w}}$$
(7)
$$\sigma_{A} = (2/c + 1)\sigma_{y} - \sigma_{x} - (2/c - 1)P_{\text{w}}$$
(8)

where \(\sigma_{A}\) is the tangential stress at the long axis point A of the elliptical borehole; \(\sigma_{B}\) is the tangential at the short axis point B of the elliptical borehole; c is the ratio of short axis b over long axis a.

When a fracture was induced at point B, if \(\sigma_{x}\) > \(\sigma_{y}\),

$$P_{\text{f}} = \{ (2c + 1)\sigma_{y} - \sigma_{x} - P_{\text{p}} + T_{0} \} /(2c - 1)$$
(9)

Combining Eq. (9) with Eqs. (1) and (2), we obtain

$$\begin{aligned} & \{ (2c - 1)P_{\text{f}} + P_{\text{p}} - T_{0} \} /\sigma_{\text{v}} + \sin^{2} (\gamma ) \\ & \quad = \{ (2c + 1)\sin^{2} (\phi - \beta ) - \cos^{2} (\phi - \beta )\cos^{2} (\gamma )\} (\sigma_{\text{H}} /\sigma_{\text{v}} ) \\ & \quad \quad + \,\{ (2c + 1)\cos^{2} (\phi - \beta ) - \sin^{2} (\phi - \beta )\cos^{2} (\gamma )\} (\sigma_{\text{h}} /\sigma_{\text{v}} ) \\ \end{aligned}$$
(10)

if \(\sigma_{x}\) < \(\sigma_{y}\),

$$P_{\text{f}} = \{ (2c + 1)\sigma_{x} - \sigma_{y} - P_{\text{p}} + T_{0} \} /(2c - 1)$$
(11)

Combining Eq. (11) with Eqs. (1) and (2), we obtain

$$\begin{aligned} & \{ (2c - 1)P_{\text{f}} + P_{\text{p}} - T_{0} \} /\sigma_{\text{v}} - (2c + 1)\sin^{2} (\gamma ) \\ & \quad = \{ (2c + 1)\cos^{2} (\phi - \beta )\cos^{2} (\gamma ) - \sin^{2} (\phi - \beta )\} (\sigma_{\text{H}} /\sigma_{\text{v}} ) \\ & \quad \quad + \,\{ (2c + 1)\sin^{2} (\phi - \beta )\cos^{2} (\gamma ) - \cos^{2} (\phi - \beta )\} (\sigma_{\text{h}} /\sigma_{\text{v}} ) \\ \end{aligned}$$
(12)

It is observed from Eqs. (10) and (12) that the equations are linear. Well deviation \(\gamma\) and azimuth \(\phi\) are constants that depend on the well geometry. For an elliptical borehole, the axis ratio c and the direction of maximum horizontal stress \(\beta\) will be known. The two unknown factors \(\sigma_{\text{H}} /\sigma_{\text{v}}\) and \(\sigma_{\text{h}} /\sigma_{\text{v}}\) are separated on the right side of the equations. If there are multiple wells or multiple points in a single well that have fractured wellbores and share the same stresses state, a system of equations can be constructed in the following matrix form:

$$[{\mathbf{P}}] = [{\mathbf{A}}][{\varvec{\upsigma}}]$$
(13)

where all parameters on the left-hand side of Eq. (10) or (12) can be lumped into the matrix [P]; the constant on the right-hand side can be included into matrix [A]; the stresses matrix can be solved by inverse operation of Eq. (13):

$$[{\varvec{\upsigma}}] = [{\mathbf{A}}]\backslash[{\mathbf{P}}]$$
(14)

The error is defined as the following:

$$[{\mathbf{e}}] = [{\mathbf{A}}][{\varvec{\upsigma}}] - [{\mathbf{P}}]$$
(15)

In actual calculation, this error will be minimized by a least-squares method. It is necessary to ensure that the determinant of matrix [A] is non-singular. It should also be noted that at least two fracture measurements are needed; the more observations than unknowns the better, to have an over-constrained system of equations. For each inversion, the magnitude of the two calculated stresses \(\sigma_{x}\) and \(\sigma_{y}\) needs to be checked and verified. If \(\sigma_{x} > \sigma_{y}\), Eq. (10) needs to be used, otherwise Eq. (12) needs to be used.

If the lengths of the two axes are very close, the c value will be close to 1. This will be a circular borehole case. In such a case, the calculation will be repeated for all \(0^{ \circ } \le \beta \le 180^{ \circ }\), the square error is calculated and plotted as a function of \(\beta\), and the minimum value of the squared error gives the direction of maximum horizontal stress and the ratios of the two horizontal stresses over vertical stress for this angle \(\beta\). Normally, there will be two \(\beta\) values that are 90° different and both have minimum squared error. Choose the one that corresponds to \(\sigma_{\text{H}} > \sigma_{\text{h}}\), but discard the other one. In matrix [P], the tensile strength \(T_{0}\) is often set to zero for circular borehole-based inversion.

In the case of elliptical boreholes, well deviation \(\gamma\), well azimuth \(\phi\), maximum horizontal stress direction \(\beta\), and axis ratio c are all known. In the inversion of two horizontal in situ stress magnitudes, a set of \(T_{0}\) values can be used for calculation. The \(T_{0}\) value corresponding to the minimum squared error will be considered as the best estimation of rock tensile strength. This is additional information to the estimated stresses in the elliptical borehole-based inversions. The ratios of the two horizontal stresses at the minimum squared error will be the estimated stress ratios.

3 Application of the method

The method has been demonstrated by a field study in West Virginia, in the southern part of the Appalachian Basin, USA. Drilling data and borehole geometry information of the MIP 3H pilot hole were used for both circular borehole-based and elliptical borehole-based in situ stress inversions.

The input data for the inversion calculation of horizontal stresses include mud weight pressure at fracture, pore pressure, vertical stress, borehole deviation, and borehole azimuth. For the cases of elliptical borehole-based in situ stress inversion, axis ratio and induced fracture azimuth are included in the input parameters. Drilling-induced fractures were reported in several sections in Middlesex and Huntersville Formations in the image log of the MIP 3H pilot hole. In this study we chose fractured sections in the Middlesex Formation, which have shown obvious ovality from caliper logs. Figure 3 shows the image log that has drilling-induced fractures in a section of the Middlesex Formation. Figure 4 shows the caliper logs at the corresponding depth section of the Middlesex Formation.

Fig. 3
figure 3

Section of image log of MIP 3H pilot hole showing induced fractures in the Middlesex Formation

Full size image
Fig. 4
figure 4

Four-arm caliper log showing the longer and shorter diameters at corresponding depth in the Middlesex Formation

Full size image

Four-arm caliper logs give the ovality of the sections that have drilling-induced fractures. In the Middlesex Formation the ratio of the two axes is around 0.978–0.984. The vertical normal stress is assumed to be equal to the weight of the overlying rock and can be computed by integrating the bulk density log data. There is no direct measurement for pore pressure in this well. Eaton’s method was applied for pore pressure estimation using acoustic slowness logging. Pore pressure was calculated from vertical stress (calculated from the density log) and the difference between actual logged data and the normal trend line of the acoustic slowness.

In the drilling process, the mud is circulated in and out of the well bore by pumping devices. Therefore, the mud pressure will be higher than the static mud weight. This is called equivalent circulating density (ECD) of mud weight. The value will be normally 3% higher than the static mud weight. The value of 1.03 times of mud weight was used in our calculation.

Table 1 lists the data prepared for the stress inversion. There are eight datasets in the Middlesex Formation. Both circular and elliptical equations were applied to the calculation.

Table 1 Data input for stress inversion in the Middlesex Formation
Full size table

Figure 5 shows the inversion results for the Middlesex Formation using the circular borehole equation. In the calculation, \(\beta\) was scanned from 0° to 180°. Two minimum squared error values of 0.0005 were found at 49° and 139°. Because at 139° the maximum horizontal stress \(\sigma_{\text{H}}\) is wrongly smaller than the minimum horizontal stress \(\sigma_{\text{h}}\), 49° (or 229°) was chosen as the direction of the maximum horizontal stress. The stress ratios \(\sigma_{\text{H}} /\sigma_{\text{v}}\) and \(\sigma_{\text{h}} /\sigma_{\text{v}}\) at this direction are 0.728 and 0.553, respectively, which are 0.75 and 0.57 psi/ft in magnitude at corresponding depth in the Middlesex Formation. The calculated maximum horizontal stress direction of 229° (or 49°) is in reasonable agreement with the field observations of the well, which were reported as 228° and 239° in the maximum horizontal stress direction at the corresponding depth in the Middlesex Formation.

Fig. 5
figure 5

Circular borehole stress inversion results for the Middlesex Formation

Full size image

In order to compare with the circular borehole-based inversion, elliptical borehole-based inversion was run. Figure 6 shows the inversion results using the elliptical equation for the Middlesex Formation. The tensile strength \(T_{0}\) was assumed a series of small values. In this case, the squared errors of all runs of the assumed strength \(T_{0}\) values are 0.002. It was not able to differentiate the satisfied T0 value having smallest error. In comparison with the circular borehole inversion, in the elliptical borehole for \(T_{0} = 0\), the stresses ratios \(\sigma_{\text{H}} /\sigma_{\text{v}}\) and \(\sigma_{\text{h}} > \sigma_{\text{v}}\) are 0.925 and 0.602, respectively, which are 0.95 and 0.62 psi/ft in magnitude of corresponding depth in the Middlesex Formation.

Fig. 6
figure 6

Elliptical borehole stress inversion results for the Middlesex Formation

Full size image

4 Discussion

Table 2 shows the comparison of the inversion results between circular borehole-based calculation and elliptical borehole-based calculation. Large differences exist between these two calculations. Tensile strengths are assumed to be zero in these two calculations for the convenience of comparison. All the input parameters are same except the axis ratio, which is unit value for a circular borehole-based calculation and 0.978–0.984 for the elliptical borehole-based calculation.

Table 2 Comparison of inversion results between circular borehole and elliptical borehole in the Middlesex Formation
Full size table

The results indicate that a 2% axis difference in an elliptical borehole will cause a 5% difference in the minimum horizontal stress calculation and a 10% difference in the maximum horizontal stress calculation. Although there is no measurement information about horizontal in situ stress magnitudes for this formation, the basin wide stress study indicated \(\sigma_{\text{h}} /\sigma_{\text{v}}\) value of up to 0.7 in the corresponding depth at this well location (Evans 1989). Evans also stated in the Appalachian Stress Study report that the magnitude of \(\sigma_{\text{H}}\) varies from high in the northern part of the basin to low values in the south; the stress state in the Devonian shale, of which Middlesex Formation is a part, is either strike-slip or normal fault regime due to the pinch-out of the underlying salt (Evans 1989). The location of the study well is around the pinch-out area (Pierce and Rich 1962). Therefore, a unit value of \(\sigma_{\text{H}} /\sigma_{\text{v}}\) stress ratio should be an upper limit. However, the estimated \(\sigma_{\text{H}} /\sigma_{\text{v}}\) stress ratio of 0.728 from circular borehole-based calculation deviates substantially from that value. With elliptical borehole inversion, the inversion results of stresses ratios \(\sigma_{\text{H}} /\sigma_{\text{v}}\) and \(\sigma_{\text{h}} /\sigma_{\text{v}}\) are 0.925 and 0.602, respectively, which are closer to the ratios reported in the Appalachian Stress Study report. It can be seen that inversion using elliptical borehole equations gives better in situ stress estimation than that by circular boreholes stress equations.

Since the inverted stress magnitudes are sensitive to the borehole diameter ratio, the accuracy of the four-arm calipers is important. If the differences are too small to be picked up by the four-arm calipers, the results will be same as the circular borehole calculations.

5 Conclusion

We can use inverse analysis to estimates of in situ horizontal stresses in an elliptical borehole from leak-off test data; case studies show that even a small amount of around 2% axis difference in an elliptical borehole will cause differences of 5%–10% in the estimation of horizontal stresses. Inversion using elliptical borehole equations gives better in situ stress estimation than those from circular borehole equations.