Container management in a single-vendor-multiple-buyer supply chain

Abstract

This paper studies a supply chain consisting of a single vendor and multiple retailers that uses returnable transport items, such as containers or crates, to facilitate shipping products from the vendor to the retailers. The paper considers two different strategies for transporting finished products from the supplier to the retailers: In case of early shipments, deliveries to a retailer can be made while the production process at the supplier is still in progress, while in the case of late shipments, the supplier has to wait until the entire production lot has been finished before shipments can be made from the lot. The paper develops mathematical models for both strategies and derives optimal solutions for the cycle time, the container size, the individual order quantities of the retailers and the shipment sequence with the intention to minimize the average total costs of the system. The behavior of the models is analyzed with the help of numerical examples.

1 Introduction

Governmental regulations and changes in customer preferences have induced companies to reduce the environmental impact of their operations. Among the various areas which have been identified as drivers of sustainable supply chain management, the distribution of products has often been characterized as a key driver of sustainability [2, 39, 51].

In transforming traditional distribution systems into more environmentally friendly ones, the transportation equipment and the packaging materials used are of major importance. More than a decade ago, Hekkert et al. [23] hypothesized that using reusable instead of one-way packaging material has the potential to reduce global CO₂ emissions from production and transportation by up to 16 %. Other studies suggested that employing reusable packaging material may reduce the gross energy requirement and waste generation of transportation significantly [39]. So-called returnable transport items (RTIs), which represent a specific type of reusable packaging material, such as pallets, crates, railcars or (maritime) containers, are used in a variety of industries today, e.g., in the automotive or consumer goods industries or the grocery sector [19, 29, 44, 46, 47].

It is clear that the use of reusable packaging material has to be adequately coordinated to fully realize the benefits this type of packaging material offers. This is especially important in case high-value or high-volume packaging material is used, whose mismanagement could lead to a significant increase in transportation cost. Management actions associated with the use of reusable packaging material include the initial purchase and the replacement of damaged or lost units, the collection and return of used items as well as the organization of cleaning and repair processes [29].

In recent years, researchers have developed models that assist decision makers in planning the purchase, distribution and return of reusable packaging material. However, as will be shown in the next section, publications in this area had a focus on conceptual models of RTI management, on the use of radio-frequency identification (RFID) in the management of RTIs and on container routing and repositioning models. Models that consider the different logistical costs associated with the use of RTIs as well as the interdependencies that arise between the management of RTIs and the distribution of finished products, in contrast, have not been proposed thus far. To close this gap, this paper studies a supplier who uses returnable packaging material for supplying a product to multiple customers. The objective is to develop a mathematical model that helps decision makers in coordinating the flow of finished products and RTIs along the supply chain and to minimize the total logistics cost of the chain.

The remainder of the paper is structured as follows. The next two sections give an overview of related works and outline the assumptions and definitions that will be used in the remaining parts of this paper. Sections 4 and 5 develop models of a supply chain with a single vendor and multiple buyers that use returnable transport items, and Sect. 6 contains numerical examples. Section 7 concludes the paper and provides suggestions for future research.

2 Literature review

Two streams of research are of special importance to this paper, namely works that focus on the management of RTIs in supply chains and works that study the coordination of replenishment decisions in single-vendor-multi-buyer supply chains. Both research streams will be discussed briefly in the following.

2.1 RTI management

Works that study returnable transport items can roughly be differentiated into three different streams of research. Papers that fall along the first stream develop mathematical models that assist decision makers in determining deployment quantities and dates for RTIs as well as the timing and quantity of replacement orders of RTIs. One example is the work of Kelle and Silver [35], who proposed different methods to forecast the expected demand and the expected returns of containers. A related paper is the one of Goh and Varaprasad [22], which developed a method for estimating the container return distribution by assuming that containers are subject to damage and loss. Buchanan and Abad [9] studied the inventory control problem for containers and considered the returns in a given period as a stochastic function of the number of containers in the field. The authors used dynamic programming to derive the optimal inventory control policy for the system.

The second stream of research studies the repositioning of containers in a logistics network. This problem is common in several scenarios, such as in international maritime shipping, the distribution of empty freight cars in a railway network or the allocation of vehicles to depots of a transport service provider. The intention of works in this area usually is to match customer demand and supply of RTIs and to minimize the number and distance of empty RTI shipments. Crainic et al. [15], for example, studied the empty container allocation problem and considered uncertain supply and demand data and several specific operational characteristics, such as the substitution of container types or product imports and exports. Del Castillo and Cochran [17] studied a manufacturer who operates several plants, which, in turn, serve multiple depots of a customer. In this scenario, the question arises which depot should return which container to which plant. The authors formulated this problem as a linear program and derived results with the help of simulation. Dang et al. [16] studied the positioning of empty containers in a port area with multiple depots. Customer demand and returning containers in depots were assumed to be serially correlated and dependent random variables. Three alternatives were considered for repositioning containers: positioning from other oversea ports, inland positioning between depots, and leasing. Related papers are those of Jordan and Turnquist [33], Choong et al. [14] and Di Francesco et al. [18], among others. A review of works that studied the empty container repositioning problem at a regional level can finally be found in [8].

The third research stream studies the use of RFID to simplify tracking and handling of RTIs. Equipping RTIs with RFID tags increases asset visibility and helps to identify which member of the supply chain holds which RTI in inventory. Hellström [24], for example, conducted a series of case studies to identify best practices in the implementation of RFID for managing and controlling RTIs. Hellström and Johansson [25] examined the impact of different control strategies on the management of returnable transport items. The results of a simulation study indicated that RTI shrinkage can be reduced by either using tracking systems or by implementing an appropriate control strategy. Related works are the ones of Johansson and Hellström [32] and Ilic et al. [29], who analyzed the impact of RFID on asset visibility and the efficiency of an RTI supply network.

2.2 Single-vendor-multi-buyer models

In recent years, research on inventory management experienced a gradual shift in perspective: while classical inventory models had a focus on individual companies, research nowadays more and more considers entire supply chains and tries to minimize inventory-related costs on the supply chain level. Early works along this stream of thought had a focus on two-stage supply chains with a single actor on each echelon, while newer works studied more complex supply networks (see [21] for a recent review).

One important issue in coordinating a single-vendor-multi-buyer supply chain is the scheduling of the buyers’ replenishment cycles and the vendor’s production cycle. If the buyers order their individually optimal order quantities, which may result from applying the economic order quantity model, for example, discrete and unequally spaced depletions of the vendor’s inventory may occur. This makes it very difficult to calculate the average inventory at the vendor and to determine how much inventory should be kept to avoid shortages. To avoid this problem, Banerjee and Burton [3] suggested to implement a common replenishment cycle for each buyer and assumed that the buyers are only allowed to order at the beginning of each cycle. The production cycle of the vendor, in turn, was assumed to be an integer multiple of the replenishment cycle to allow the vendor to economize on setup costs. This paper was extended by Viswanathan and Piplani [48], who assumed that the vendor offers a price discount to the buyers to induce them to deviate from their individually optimal order quantities and to participate in the cooperation. Another extension was proposed by Siajadi et al. [45], who assumed that the production cycle of the vendor and the replenishment cycles of the buyers are of equal sizes. In addition, they assumed that the product is delivered in equal-sized batches to the buyers and that the number of shipments may differ from buyer to buyer. Hoque [26] extended the work of Siajadi et al. [45] by studying three alternative shipment policies: two with equal-sized batches and one with unequal-sized ones. Kim et al. [37] developed a model that considered the procurement of raw material as well as the production and delivery of multiple items to multiple retailers. The authors considered the production sequence as a key decision factor for effectively coordinating procurement, production and delivery activities.

Implementing a single replenishment cycle for all buyers may be very restrictive in certain scenarios, for example, when there is a significant difference between the cost parameters of the buyers. To provide a more flexible solution for such situations, Abdul-Jalbar et al. [1] relaxed the assumption of a common replenishment cycle and assumed that the order interval of each buyer is an integer multiple of the order interval of the buyer who is scheduled before this buyer in the sequence of deliveries. Thus, by sorting the buyers and by calculating different replenishment intervals, the total costs of the system can be reduced. Chan and Kingsman [10] suggested a different coordination mechanism and implemented a basic cycle approach, where the replenishment interval of each buyer is restricted to integer multiples of the basic cycle. This coordination mechanism was adopted by Chan et al. [11] and Chan and Lee [12], among others.

Other authors extended these models by including further stages of the supply chain in their study, for example, distributors or raw material suppliers. Banerjee et al. [4], for instance, considered a supply chain consisting of a single manufacturer, multiple suppliers and multiple buyers. The production cycle of the manufacturer was assumed to be an integer multiple of the replenishment cycle of the buyers. Ben-Daya and Al-Nasser [6] developed a model of a three-stage supply chain with multiple actors on each stage and assumed that the cycle time of each stage is an integer multiple of the cycle time of the adjacent downstream stage. Related works are the ones of Khouja [36], Wee and Yang [49], Jaber and Goyal [30] and Sarker and Diponegoro [43], among others. Other extensions included consignment stock policies [5, 7], deteriorating items [28, 52], learning effects in production [40], order cost reduction [50] and lead time reduction [27, 31].

2.3 Synthesis of both research streams

The literature review illustrates that research on returnable transport items and on supply chain inventory models has thus far been conducted widely independently of each other. Considering the management of reusable packaging material in an integrated inventory model, however, may lead to many benefits. If the production and distribution of finished products and the distribution and return of RTIs are adequately coordinated, this may lead to lower levels of RTI inventory in the supply chain and fewer stockout situations. Both aspects contribute to lower total system costs. The only work we are aware of that studied RTIs in an integrated inventory model is the one of Kim et al. [38], which, however, considered only a single vendor and a single retailer in modelling their supply chain. It is obvious that the planning problem changes if multiple retailers are considered, which requires that the sequence of deliveries to the retailers (and the sequence of returns from the retailers) is determined in addition. This paper extends the existing literature by developing a model that considers the coordination of finished products and RTIs in a supply chain consisting of a single vendor and multiple retailers.

3 Problem description

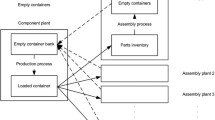
This paper considers a single vendor (supplier) who produces a product and delivers it to multiple buyers (retailers). Before shipping the finished products to the retailers, the items are stored away in containers (for example, to facilitate handling or to protect the products from damages in transit). After products have been removed from the containers at the retailers, used containers are returned to the vendor for potential reuse. This scenario is illustrated in Fig. 1.

Fig. 1

Operational structure of a single-vendor-multiple-buyer environment

Apart from the assumptions already stated, we assume the following hereafter:

• 1. End-customer demand at the retailers is deterministic and constant over time.

• 2. The supplier uses one type of RTI for shipping products to the retailers.

• 3. After a shipment arrives at one of the retailers, the retailer empties the RTIs and subjects them to a cleaning and repair process. After a lead time of l _i units of time, which is required for preparing the RTIs for their next usage, the empty RTIs arrive at the supplier.

• 4. The paper considers two types of production processes. If the first one is implemented, the supplier has to wait until the entire lot has been finished before shipments can be made from the lot. If the second one is used, the supplier can make shipments to the buyers while the production process is still in progress. Both production processes are representative for different scenarios and have often been studied in the literature. We refer to the first production process as the case of “late shipments” and to the second one as the case of “early shipments.”

• 5. To coordinate production and consumption, the supplier implements a common replenishment cycle for all retailers and replenishes each retailer exactly once per cycle.

The scenario studied in this paper is representative for a variety of different application areas, as can be shown by evaluating case studies that are available in the literature. Hellström and Johansson [25], for example, presented a case study of a Swedish dairy company that uses RTIs for transporting dairy products to different retail outlets. After RTIs have been emptied, they are returned to the dairy company and reused. Hellström and Johansson described the demand for RTIs during their observation period as stable without seasonal peaks. Similar results were obtained by Chew et al. [13], who reported a small standard deviation in the demand rate of RTIs. Kärkkäinen et al. [34] presented and evaluated nine case studies on the use of RTIs and showed that in many cases, RTIs were tracked by one of the parties involved, which renders RTI demand and RTI returns predictable. Similar cases were described by Rosenau et al. [42]. These case studies illustrate that scenarios with (almost) static and deterministic demand for RTIs may occur frequently in practice.

In developing the proposed model, the following notation will be used:

n :

Number of retailers

p :

Production rate of the supplier in units per year

S :

Setup cost in dollars per setup

h _R :

Inventory holding cost for RTIs in dollars per unit per year

h _F :

Inventory holding cost for finished goods in dollars per unit per year

c _α :

Annual cost of managing a container, including depreciation and repair, per unit container capacity

s :

Scale factor for container capacity affecting the annual cost of managing a container

d :

Demand rate at the supplier in units per year, where $d={\sum }_{i=1}^n{d}_i$

d _i :

Demand rate at retailer i in units per year

h _i :

Inventory holding cost for finished goods at retailer i in dollars per unit per year

A _i :

Ordering cost of retailer i in dollars per order

l _i :

RTI return lead time of retailer i in years

T :

Cycle length in years

r _i :

Amount of RTIs required for a single delivery to retailer i, where $r_i=⌈\frac{d_{i}T}{\mathit{\alpha }}⌉$

Z :

Shipment sequence

Α :

Container capacity in units, where α ∈ [α_min, α_max]

d _max :

Maximum demand rate at the retailers in units per year, i.e., $d_{\max }={\max }_{1\le i\le n}\left\{d_i\right\}$

q _i :

Shipment quantity per delivery for retailer i in units, where q _i  = d _i T

Q :

Production lot size in units, where $Q={\sum }_{i=1}^n{q}_i$

l :

Sum of RTI return lead times in years, i.e., $l={\sum }_{i=1}^n{l}_i$

r _max :

Maximum amount of available RTIs at the manufacturer, where r_max = max_1≤i≤n{r _i }

T _max :

Maximum possible cycle time in years

T _min :

Minimum possible cycle time in years

Note that squared brackets in the indices are used to indicate where the sequence of the buyers influences the respective cost component. Thus, the index ₁ denotes the first supplier (as per parameter definition), whereas _[1] denotes the buyer first in sequence.

4 Model 1: Late shipments

4.1 The objective function

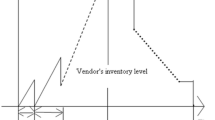
The first model studies the case where shipments from a lot can only be made after the entire lot has been finished. Figure 2 illustrates the related inventory patterns for empty containers and finished goods for a vendor and three retailers. As can be seen, the supplier minimizes the number of RTIs needed in the system using only as many RTIs as are required to ship the largest batch to one of the retailers, i.e., r_max. Such a policy is beneficial in case RTIs are expensive or storage space for RTIs is limited. The consequence of this policy, however, is that the supplier has to ship batches consecutively to the retailers, which leads to an increase in finished products inventory (cf. Fig. 2).

Fig. 2

Inventory patterns for empty containers and finished goods (n = 3) for the case of late shipments

The sequence of events is as follows: At the beginning of a cycle, the supplier starts producing the final product and finishes production after ${\sum }_{i=1}^n{q}_i/p$ units of time. Subsequently, a shipment to retailer i is made, who receives the batch and subjects the RTIs to a screening and repair process. After l _i units of time, the empty RTIs arrive at the supplier, who despatches a shipment to one of the retailers who has not yet been served in this cycle (if any). Note that the sequence in which the retailers are served influences the total costs of the system, first by determining how many finished products are removed from the inventory of the supplier (this favors that large shipments are made early in the sequence) and second by determining how long the supplier has to wait before the next shipment can be made (this favors that shipments to retailers with short return lead times are made early in the sequence).

The total costs for the system described above are formulated as follows (cf. Appendix 1 for a derivation of this cost function):

$$\begin{aligned} TRC\left( {\alpha ,T,Z} \right)_{{M_{1} }} & = \frac{{\left( {s + \mathop \sum \nolimits_{i = 1}^{n} A_{i} - h_{R} \mathop \sum \nolimits_{i = 1}^{n} r_{i} l_{i} } \right)}}{T} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d^{2} }}{2p}} \right)T \\ & \quad + h_{R} r_{{\rm max} } + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} + c_{\alpha } \alpha^{s} r_{{\rm max} } , \\ \end{aligned}$$

(1)

where $d={\sum }_{i=1}^n{d}_i$ and $r_i=\frac{d_{i}T}{\mathit{\alpha }},\forall i.$

s denotes a scale parameter that determines how the container capacity impacts the cost of managing a container. If s > 1, then managing one capacity unit of a large container leads to higher costs than managing one capacity unit of a small container, which could be the case if large containers are more difficult to repair than small ones, for example. If s < 1, in contrast, then scale effects occur, and the cost of managing one capacity unit is reduced as the size of the container increases.

4.2 Solution of the model

As was explained above, the shipment schedule is a critical decision variable in reducing inventory holding costs. Since one shipment has to be made to each retailer per cycle, the other components of the total cost function are not affected by the sequence of shipments. In other words, the shipment schedule itself is a decision that is independent of the other decision variables. As is shown in Appendix 2, the shipment schedule should be established to keep the following condition:

$$\frac{{d_{\left[ i \right]} }}{{l_{\left[ i \right]} }} \ge \frac{{d_{{\left[ {i + 1} \right]}} }}{{l_{{\left[ {i + 1} \right]}} }},\quad {\text{ where}}\,\,\,i = 1, 2, \ldots ,n{-} 1.$$

(2)

If the shipment schedule is established according to Eq. (2), then we can assume that the shipment sequence has been established prior to assigning values to the other decision variables. By definition, the number of required RTIs should be an integer value. Due to this restriction, it is difficult to find a solution for the objective function analytically. Therefore, we relax the integral condition defined above, i.e., $r_i=⌈\frac{d_{i}T}{\mathit{\alpha }}⌉,\forall i$, in the following and treat the number of required RTIs as a continuous variable, i.e., $r_i=\frac{d_{i}T}{\mathit{\alpha }},\forall i$. Similarly, the value of r_max is relaxed as $\frac{d_{\max }T}{\mathit{\alpha }}$, where d_max = max_1≤i≤n{d _i }.

The total cost function given in Eq. (1) can now be simplified as follows:

$$\begin{aligned} TRC\left( {\alpha ,T,Z} \right)_{{M_{1} }} & = \frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} } \right)}}{T} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d^{2} }}{2p} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } } \right)T \\ & \quad - \frac{{h_{R} \mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{\alpha } + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} . \\ \end{aligned}$$

(3)

To generate a feasible schedule, the cycle length should satisfy the condition $(\frac{Q}{p}+{\sum }_{i=1}^n{l}_i)\le T$. The lower bound of the cycle length could thus be set to $T_{min}=\frac{{\sum }_{i=1}^n{l}_i}{(1-\frac{d}{p})}$.

To find an optimal solution to the problem, it would be necessary to establish the Karush–Kuhn–Tucker conditions of Eq. (3) and the constraints on T and α. Due to the complexity of the objective function, this is not possible. We are, however, able to show that the objective function (3) is either convex or concave in T and α for given values of the respective other decision variable, depending on the parameter values. This enables us to find a solution for T and α that is at least locally optimal.

If the optimal shipment schedule Z is given, the first and second derivatives of $TRC{\left(\mathit{\alpha },T|Z\right)}_{M_1}$ with respect to α can be derived as follows:

$$\frac{{\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{\partial \alpha } = \left( { - \frac{{h_{R} }}{{\alpha^{2} }}\left( {1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } T}}} \right) + (s - 1)c_{\alpha } \alpha^{s - 2} } \right)d_{{\rm max} } T,$$

(4a)

$$\frac{{\partial^{2} TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{{\partial \alpha^{2} }} = \left( {\frac{{2h_{R} }}{{\alpha^{3} }}\left( {1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } T}}} \right) + (s - 1)(s - 2)c_{\alpha } \alpha^{s - 3} } \right)d_{{\rm max} } T.$$

(4b)

From Eqs. (4a) and (4b), we can derive the following closed-form expressions satisfying $\frac{\mathit{\partial }TRC{(\mathit{\alpha },T|Z)}_{M_1}}{\mathit{\partial }\mathit{\alpha }}=0$ and $\frac{{\mathit{\partial }}^{2}TRC{(\mathit{\alpha },T|Z)}_{M_1}}{\mathit{\partial }{\mathit{\alpha }}^2}=0$, respectively:

$$\alpha^{0} = \left( {\frac{{h_{R} }}{{\left( {s - 1} \right)c_{\alpha } }}\left( {1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } T}}} \right)} \right)^{\frac{1}{s}} {\text{satisfying}}\,\,\,\,\frac{{\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{\partial \alpha } = 0 ,$$

(5a)

$$\alpha^{b} = \left( {\frac{{2h_{R} }}{{\left( {1 - s} \right)\left( {s - 2} \right)c_{\alpha } }}\left( {1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } T}}} \right)} \right)^{\frac{1}{s}} {\text{satisfying}}\,\,\,\,\frac{{\partial^{2} TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{{\partial \alpha^{2} }} = 0.$$

(5b)

From Eq. (4b), it follows that $TRC{\left(\mathit{\alpha },T|Z\right)}_{M_1}$ can be either a concave or a convex function in α. If the function is convex, then the stationary point given in Eq. (5a) should be realized, while in the case of a concave function, one of the boundary values of α (i.e., either α_min or α_max) constitutes the locally optimal solution. Note that α⁰ is the only stationary point of the objective function; therefore, we can conclude that the function value increases for values >α⁰, although the objective function may be concave in this region. Depending on the specific values of T and s, the container capacity of the system should be selected as given in Table 1.

Table 1 Optimal container capacity for different values of T and s

For both Cases 1.2 and 2.1, we note that the inequality α⁰ < α^b is always satisfied, as is shown in Appendix 3. In addition, a more detailed analysis of the patterns of $TRC{\left(\mathit{\alpha },T|Z\right)}_{M_1}$ for Cases 1.2 and 2.1 is provided in Appendix 4.

The first and second partial derivatives of $TRC{\left(\mathit{\alpha },T|Z\right)}_{M_1}$ with respect to T are given as

$$\frac{{\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{\partial T} = - \frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} } \right)}}{{T^{2} }} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d^{2} }}{2p} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } } \right),$$

(6a)

$$\frac{{\partial^{2} TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{{\partial T^{2} }} = \frac{{2\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} } \right)}}{{T^{3} }}.$$

(6b)

As can be seen, for given values of α, $TRC{\left(\mathit{\alpha },T|Z\right)}_{M_1}$ is convex in T. From Eq. (6a), we obtain the following expression:

$$\begin{aligned} T^{*} \left( {\alpha |Z} \right) & = {\rm max} \left( {T^{0} \left( {\alpha |Z} \right),T_{{\rm min} } } \right),{\text{ where}} \\ T^{0} \left( {\alpha |Z} \right) & = \sqrt {\frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} } \right)}}{{\left( {\mathop \sum \nolimits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d^{2} }}{2p} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } } \right)}}} . \\ \end{aligned}$$

(7)

We establish the following solution procedure to solve the proposed model:

Solution procedure

• Step 1. (Shipment schedule)

  First, the optimal delivery sequence within a single cycle, Z^*, is established by sorting the retailers according to the sequencing rule $\frac{d_{\left[i\right]}}{l_{\left[i\right]}}\ge \frac{d_{\left[i+1\right]}}{l_{\left[i+1\right]}},i=1,2,\dots ,n-1.$

• Step 2. (Container capacity and cycle length)

  Secondly, iteratively determine both container capacity, α, and cycle length, T. In the initialization step, select α_min as a starting value for α.

  • Step 2.1. (Initialization step) k = 1, ${\mathit{\alpha }}_{(1)}^{\ast }={\mathit{\alpha }}_{\min }$

  • Step 2.2. (Iteration step) k = k + 1

    • First, calculate the optimal cycle length using the current value of ${\mathit{\alpha }}_{(k-1)}^{\ast }$ with the help of Eq. (7). Secondly, obtain the optimal value for ${\mathit{\alpha }}_{(k)}^{\ast }$ from $T_{(k)}^{\ast }$ according to Table 1.

  If $\left|T_{(k)}^{\ast }-T_{(k-1)}^{\ast }\right|\le \mathit{\epsilon }$, then go to Step 3. Otherwise, go to Step 2.2.

• Step 3. (Shipment lot size)

  Using both cycle length and container capacity, calculate the shipment lot size for finished goods and RTIs: $q_{\text{i}}^{\ast }=d_{\text{i}}{T}^{\ast },r_{\text{i}}^{\ast }=⌈\frac{q_i^{\ast }}{{\mathit{\alpha }}^{\ast }}⌉,\forall i.$

5 Model 2: Early shipments

5.1 The objective function

The second model studies the case where shipments from a lot can be made while the production process of the lot is still in progress. In such a situation, the first batch is delivered to one of the buyers directly after its completion. Figure 3 illustrates the related inventory patterns for empty containers and finished goods for a vendor and three retailers. As can be seen, the only difference between this shipment policy and the one discussed in Sect. 4 is that shipments are dispatched earlier, which leads to lower finished products inventory at the supplier.

Fig. 3

Inventory patterns for empty containers and finished goods (n = 3) for the case of early shipments

The total costs for the system described above are formulated as follows (Note that the derivation of this cost function is presented in Appendix 5):

$$\begin{aligned} TRC\left( {\alpha ,T,Z} \right)_{{M_{2} }} & = \frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} } \right)}}{T} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d\left( {2d_{[1]} - d} \right)}}{2P} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } } \right)T \\ & \quad - \frac{{h_{R} \mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{\alpha } + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{\left[ j \right]} , \\ \end{aligned}$$

(8)

where $d={\sum }_{i=1}^n{d}_i$ and $r_i=⌈\frac{d_{i}T}{\mathit{\alpha }}⌉,\forall i$

To assure that the average inventory level does not become negative, the following feasibility condition needs to be satisfied (see Appendix 5):

$$T_{{\rm min} } \le T^{*} \le T_{{\rm max} } ,\,{\text{where}}\,\,\,\,T_{{\rm min} } = \frac{{Pl_{[n]} }}{{d_{[1]} }}\,\,{\text{and}}\,\,T_{{\rm max} } = \frac{{P\left( {l - l_{[n]} } \right)}}{{\left( {d - d_{[1]} } \right)}}.$$

(9)

From Eq. (9), we derive the feasibility condition for any shipment sequence from the inequality of both bounds, i.e., T_min ≤ T_max, as seen below:

$$\frac{{d_{[1]} }}{{l_{[n]} }} \ge \frac{d}{l}.$$

(10)

5.2 Solution of the model

By comparing Eqs. (1) and (8), it can be seen that both cost functions differ only in a single cost term. This difference is caused by the different inventory carrying costs of the supplier in both models. As a result, the solution of both models is similar.

For a given sequence of shipments, we calculate the first partial derivative of the relaxed total cost function with respect to α. It can be seen that the optimality condition for RTI capacity is the same as the one given in Sect. 4.2. After calculating the first partial derivative of $TRC{\left(\mathit{\alpha },T|Z\right)}_{M_2}$ with respect to T, the following expression for the optimal cycle time can be derived, which is different from the one given in Eq. (8):

$$T^{*} \left( {\alpha |Z} \right) = {\rm min} \left( {{\rm max} \left( {T^{0} \left( {\alpha |Z} \right),T_{{\rm min} } } \right),T_{{\rm max} } } \right),$$

(11)

where $T^0(\mathit{\alpha }|Z)=\sqrt{\frac{(S+{\sum }_{i=1}^n{A}_i)}{{\sum }_{i=1}^n\frac{h_i{d}_i}{2}+\frac{h_{F}d(2d_{[1]}-d)}{2P}+(\frac{h_R}{\mathit{\alpha }}+c_{\mathit{\alpha }}{\mathit{\alpha }}^{s-1})d_{\max }}}.$

The solution procedure developed in Sect. 4.2 can now easily be adopted to find an optimal solution to Model 2.

Solution procedure

• Step 1. (Shipment schedule)

  Generate all possible shipment sequences using full enumeration. Run Step 2 and Step 3 consecutively and then select the best shipment schedule among the feasible sequences.

• Step 2. (Container capacity and cycle length)

  • Step 2.1. Select a shipment sequence and check its feasibility with the help of condition (10). If the shipment sequence violates this condition, repeat Step 2.1 for evaluating the next sequence.

  • Step 2.2. (Initialization step) k = 1, ${\mathit{\alpha }}_{(1)}^{\ast }={\mathit{\alpha }}_{\min }$.

  • Step 2.3. (Iteration step) k = k + 1.

    First, calculate the optimal cycle length using the current value of ${\mathit{\alpha }}_{(k-1)}^{\ast }$ with the help of Eq. (11). Secondly, obtain the optimal value for ${\mathit{\alpha }}_{(k)}^{\ast }$ from $T_{(k)}^{\ast }$ according to Table 1. If $\left|T_{(k)}^{\ast }-T_{(k-1)}^{\ast }\right|\le \mathit{\epsilon }$, then go to Step 3. Otherwise, go to Step 2.2.

• Step 3. (Shipment lot size)

  Using both cycle length and container capacity, calculate the shipment lot size for finished goods and RTIs: $q_{\text{i}}^{\ast }=d_{\text{i}}{T}^{\ast },r_{\text{i}}^{\ast }=⌈\frac{q_i^{\ast }}{{\mathit{\alpha }}^{\ast }}⌉,\forall i.$

6 Numerical studies

6.1 Illustrative example

This section provides an illustrative example where a single vendor supplies a finished product to four retailers. Table 2 contains the data set used in this example.

Table 2 Sample data set

To analyze the benefit that results for the supply chain from coordination, we compare the costs of the integrated models with the case of non-coordination. In the non-coordinated models, we assume that the supplier determines the production–delivery policy without considering the retailers’ cost information (cf. Appendix 6 for the non-coordinated models).

• Case 1. Late shipments

  First, the case where the production lot has to be finished before a shipment can be made from the lot is considered. Using the proposed solution procedure for Model 1, the other decision variables of the optimal shipment policy were obtained as follows:

• Case 1.1. Integrated model with late shipments (M1)

  Z^* = {1, 3, 2, 4}, α^* = 4.5132, T^* = 0.1219, q^* = (146, 88, 100, 73), r^* = (33, 20, 23, 17) and $TR{C}_{M_1}=4,670.9.$

  The results indicate that it is optimal to design containers with a capacity of approximately 4.5 units and to operate a total of 33 containers in the system to accommodate the retailers’ demand. Shipment quantities for each delivery to the retailers are set as above.

• Case 1.2. Non-coordinated model with late shipments (N1)

  Z^* = {1, 3, 2, 4}, α^* = 4.4368, T^* = 0.1062, q^* = (127, 76, 87, 63), r^* = (29, 18, 20, 15) and $TR{C}_{N_1}=4,713.9.$

  As can be seen, in the case on non-coordination, smaller batch sizes are transported from the supplier to the buyers, which results in fewer containers that are operated in the system. The total cost of the system is higher as compared to the coordinated case.

• Case 2. Early shipments

  In a second step, we consider the case where shipments from a lot can be made while the production process is still in progress. Using the proposed solution procedure for Model 2, the other decision variables of the optimal shipment policy are obtained as follows:

• Case 2.1. Integrated model with early shipments (M2)

  Z^* = {1, 2, 4, 3}, α^* = 4.4683, T^* = 0.1168, q^* = (140, 84, 96, 70), r^* = (32, 19, 22, 16) and $TR{C}_{M_2}=4,261.0.$

  The results indicate that it is optimal to design containers with a capacity of approximately 4.5 units and to operate a total of 32 containers in the system to accommodate the retailers’ demand. Thus, it becomes clear that in this example, the size of the containers is not changed; permitting early batch shipments, however, reduces total cost, which can be attributed to lower inventory carrying costs that result from earlier inventory depletions.

• Case 2.2. Non-coordinated model with early shipments (N2)

  Z^* = {1, 3, 2, 4}, α^* = 4.4683, T^* = 0.1121, q^* = (135, 81, 92, 67), r^* = (31, 19, 21, 16) and $TR{C}_{N_2}=4,269.8$.

  Again, batch sizes are smaller in the non-coordinated case as compared to the coordinated case, and fewer containers are operated in the system. Again, non-cooperation leads to an increase in total relevant cost.

6.2 Analysis of $TR{C}_{M_2}/TR{C}_{M_1}$

To gain further insights into the behavior of the model, we conducted a simulation study with a set of 10,000 randomly generated data sets. To generate the parameter values, the ranges presented in Table 3 were employed, and parameters were selected from the ranges with equal probability.

Table 3 Parameter ranges used in the generation of the random data sets

Table 4 contains the results of a regression analysis which studied the impact of the model parameters on the ratio of the total relevant costs of both models M1 and M2 (coordinated cases). As can be seen, an increase in the demand rate d _i or the RTI return lead time l _i leads to a reduction in the ratio $TR{C}_{M_2}/TR{C}_{M_1}$ [i.e., the ratio of Eqs. (3)–(8)]. Obviously, the higher the individual demand rates of the retailers or the higher the RTI return lead times, the higher are the total relevant cost of Model 1 as compared to Model 2. This can be explained as follows: The inventory level of Model 1 is, in general, higher than the inventory level of Model 2, as shipments are made earlier in Model 2. This leads to an earlier initiation of the consumption process in this model. For higher individual demand rates of retailer i, ceteris paribus, more inventory has to be kept in stock. The higher the total inventory that has to be kept in the system, the more beneficial it becomes to ship batches early to the buyers, which leads to a cost advantage of Model 2. Similarly, as the individual RTI return lead times increase, batches have to be kept in stock longer, which increases inventory. In this case, it is again beneficial to ship batches early to the buyers. Another model parameter that has a significant impact on the ratio $TR{C}_{M_2}/TR{C}_{M_1}$ is the production rate of the supplier, p. The higher the production rate, the lower is the relative cost advantage of Model 2. Obviously, the faster the supplier produces, the earlier the first batch is finished and the earlier it can be shipped to one of the buyers. This reduces the inventory level in both models, but the reduction is larger for Model 1 than for Model 2. The production rate further enhances the impact of the demand rate d _i . If the production rate is large, as compared to the individual demand rates, then a shipment to one of the retailers only leads to a small reduction in total inventory, which results in a high average inventory, and vice versa. This, again, reduces the cost advantage of Model 2. The cost of carrying finished products in inventory at the supplier, h _F , and the cost of keeping finished products at the buyers, h _i , also impact the ratio $TR{C}_{M_2}/TR{C}_{M_1}$. Since the inventory level of Model 1 is typically higher than the inventory level of Model 2, higher costs of carrying inventory at the supplier increase the cost advantage of Model 2. An increase in h _i has an opposite effect on the cost ratio. Finally, also the rate parameter s influences the ratio $TR{C}_{M_2}/TR{C}_{M_1}$. As can be seen in Table 4, an increase in s leads to an increase in the cost advantage of Model 2. Obviously, if no scale effects occur in managing containers and if large containers are needed, then it is beneficial for the supplier to reduce its inventory of finished products, as this makes the use of small containers more economical. Since the early shipment policy M₂ leads to a lower overall inventory level at the supplier, this policy has a relative cost advantage over the late shipment policy if the parameter s is high. A similar result was obtained for the annual cost of managing a container, c _α .

Table 4 Results of a regression analysis between the model parameters and the ratio $TR{C}_{M_2}/TR{C}_{M_1}$

For a practical application, this result implies the following: Typically, the question whether Model 1 or 2 can be implemented in practice is dictated by the technical requirements of the production process. However, these requirements can often be changed if an investment is made. Thus, based on our results, we recommend that companies check whether a shift to a production process that permits early batch shipments is profitable in case the demand rates of the retailers are high or the RTI return lead times are long. Such a scenario could arise, for example, if products are distributed internationally.

6.3 Analysis of the relative advantage of coordination

This section analyzes the relative advantage of coordination as compared to the non-cooperative cases. Table 5 contains the results of a regression analysis which studied the impact of the model parameters on the ratio of the total relevant costs of both models M1 and N1. As can be seen, an increase in the inventory holding cost for finished goods at the supplier, h _F , reduces the relative advantage of coordination. This is the result of larger batch sizes in the coordinated case, which leads to higher inventory at the supplier. Note that the term “relative advantage” refers to the cost difference between the coordinated and uncoordinated model. Coordination is always superior to non-coordination from a systems perspective, so the relative advantage is always positive. The inventory carrying costs at the buyers, h _i , have an opposite effect on the relative advantage of coordination. As h _i increases, the relative advantage of coordination increases as well.

Table 5 Results of a regression analysis between the model parameters and the ratio $TR{C}_{N_1}/TR{C}_{M_1}$

Table 6 contains the results of a regression analysis on the relative advantage of the coordinated Model 2 over the non-coordinated case. As can be seen, the relationship between the model parameters and the cost ratio is similar than the relationships displayed in Table 5.

Table 6 Results of a regression analysis between the model parameters and the ratio $TR{C}_{N_2}/TR{C}_{M_2}$

Figure 4 compares the relative efficiency of the coordinated policies for both shipment structures studied in this paper. The relative efficiency of the models was calculated as follows:

$$RE_{1} = TRC_{{N_{1} }} /TRC_{{M_{1} }} ,$$

$$RE_{2} = TRC_{{N_{2} }} /TRC_{{M_{2} }} .$$

Fig. 4

Comparison of the relative efficiency of both shipment policies

As can be seen in Fig. 4, the relative efficiency of the early shipment policy is, on average, much higher than the relative efficiency of the late shipment policy.

7 Conclusions and suggestions for future research

This paper studied a supply chain consisting of a single vendor and multiple retailers that uses returnable transport items to facilitate shipping products from the vendor to the retailers. The paper developed models for two different shipment strategies and derived optimal solutions for the cycle time, the container size, the individual order quantities of the retailers and the shipment sequence with the intention to minimize the average total costs of the system. The behavior of the models was analyzed with the help of numerical examples.

The results of the paper indicate that the individual demand rates of the retailers and their respective RTI return lead times are critical for the performance of the models. It was shown that shipping batches to the retailers while the production process of the supplier is still in progress is especially beneficial in case the individual demand rates of the retailers are low (as compared to the supplier’s production rate) and the return lead times for RTIs are high. Further, the analysis indicated that the supplier should use few containers with a relatively large capacity if the individual demand rates are low and the RTI return lead times are high, and many containers with a relatively low capacity in the opposite case.

The model developed in this paper has limitations. First, it was assumed that the cost of keeping RTIs in inventory are independent of the capacity (and therewith size) of the containers. In practice, however, we may assume that different container sizes require different amounts of storage spaces (e.g., a 20′ container vs. a 40′ container), which would result in inventory carrying costs that depend on the capacity of the RTI. Secondly, this paper assumed that the capacity of an RTI can be chosen freely within given limits. In a practical application, however, the supplier may face a discrete number of different types of RTIs out of which he or she has to choose (e.g., in the case of maritime containers), or he or she may face restrictions imposed by a transport service provider. In such a case, it would be necessary to include these constraints in the optimization problem developed in this paper, or to test a given set of container sizes for optimality. We note, however, that our model could act as a heuristic in such a case, as it would give the decision maker an idea as to which container types could in principle be suitable candidates for the supply chain. Thirdly, we assumed in developing the proposed models that the supplier tries to minimize the overall amount of RTIs in the system and that only as many RTIs are kept in stock as are needed to ship the largest batch quantity to the retailers. A different strategy would be to increase the maximum RTI level in the system, which would enable the supplier to ship a second batch before the RTI return shipment of the first batch has been received. Furthermore, our analysis showed that the return lead time of empty RTIs is critical for the performance of both models. In a next step, it would be interesting to study different practices that help the buyers to return empty RTIs quicker to the supplier. In addition, it would be interesting to introduce a stochastic component into the model to analyze how long RTI return lead times influence the performance of the system if demand is uncertain or how production and distribution should be coordinated if the return lead times are stochastic themselves. Finally, the centralized models developed in this paper presuppose that a central planner exists that has access to cost parameters both at the supplier and the buyers. It is obvious that in a practical scenario, getting access to the required data may be very difficult. We note, however, that the cost reductions that can be obtained with the help of cooperative planning may act as an incentive for the parties involved to disclose the required information, as all parties that participate in the cooperation can improve their individual positions if the cooperation gain is adequately distributed. If the parties are not willing to cooperate, then incentive mechanisms, such as trade credits or quantity discounts, might have to be implemented. These, and other related issues, should be addressed in an extension of this paper.

Appendices

Appendix 1

The time-weighted average inventory for empty RTIs at the vendor can be derived with the help of Fig. 2:

$${\text{Avg}} . {\text{Inv}}_{R} = \frac{{r_{{\rm max} } \left( {T - \mathop \sum \nolimits_{i = 1}^{n} l_{i} } \right) + \mathop \sum \nolimits_{i = 1}^{n} \left( {r_{{\rm max} } - r_{i} } \right)l_{i} }}{T} = \left( {r_{{\rm max} } - \frac{{\mathop \sum \nolimits_{i = 1}^{n} r_{i} l_{i} }}{T}} \right).$$

(12)

The time-weighted average inventory for finished products at the vendor can be calculated as follows (see Fig. 2):

$$\begin{aligned} {\text{Avg}} . {\text{Inv}}_{F} & = \frac{{\frac{{Q^{2} }}{2p} + l_{\left[ 1 \right]} \left( {Q - d_{\left[ 1 \right]} T} \right) + l_{\left[ 2 \right]} \left( {Q - d_{\left[ 1 \right]} T - d_{\left[ 2 \right]} T} \right) + \cdots + l_{{\left[ {n - 1} \right]}} \left( {Q - d_{\left[ 1 \right]} T - d_{\left[ 2 \right]} T - \cdots - d_{{\left[ {n - 1} \right]}} T} \right)}}{T} \\ \, & \, = \frac{{d^{2} T}}{2p} + \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} , \\ \end{aligned}$$

(13)

where Q denotes the production lot size of the supplier with Q = dT.

The total cost function can now be formulated as follows:

$$\begin{aligned} TRC\left( {\alpha ,T,Z} \right)_{{M_{1} }} & = \frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} } \right)}}{T} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2}T} \right) + h_{R} \left( {r_{{\rm max} } - \frac{{\mathop \sum \nolimits_{i = 1}^{n} r_{i} l_{i} }}{T}} \right) \\ & \quad + h_{F} \left( {\frac{{d^{2} }}{2p}T + \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} } \right) + c_{\alpha } \alpha^{s} r_{{\rm max} } \\ & = \frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} - h_{R} \mathop \sum \nolimits_{i = 1}^{n} r_{i} l_{i} } \right)}}{T} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d^{2} }}{2p}} \right)T + h_{R} r_{{\rm max} } \\ & \quad + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} + c_{\alpha } \alpha^{s} r_{{\rm max} } . \\ \end{aligned}$$

(14)

Appendix 2

Equation (3) shows that the average inventory level for finished goods is solely affected by the shipment schedule for a given T. Thus, the part of the cost function which is affected by the shipment schedule is given as follows:

$$\begin{aligned} G\left( Z \right) & = h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} \\ & = h_{F} \left( { \mathop \sum \limits_{i = 1}^{k - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} + l_{[k]} \mathop \sum \limits_{j = k + 1}^{n} d_{[j]} + l_{[k + 1]} \mathop \sum \limits_{j = k + 2}^{n} d_{[j]} + \mathop \sum \limits_{i = k + 2}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} } \right). \\ \end{aligned}$$

(15)

Consider an arbitrary shipment schedule Z _a . Subsequently, compose another shipment schedule Z _b by exchanging two consecutive retailers, for example, k and k + 1. The difference in total costs for these two shipment schedules can then be calculated as:

$$\begin{aligned} & TRC\left( {\alpha ,T\left( \alpha \right),Z_{a} } \right)_{{M_{1} }} - TRC\left( {\alpha ,T\left( \alpha \right),Z_{b} } \right)_{{M_{1} }} = G\left( {Z_{a} } \right) - G\left( {Z_{b} } \right) \\ & \quad = h_{F} \left( {l_{[k]} \left( {\mathop \sum \limits_{j = k}^{n} d_{[j]} - d_{[k]} } \right) + l_{[k + 1]} \left( {\mathop \sum \limits_{j = k}^{n} d_{[j]} - d_{[k]} - d_{[k + 1]} } \right)} \right) \\ & \quad \quad - h_{F} \left( {l_{[k + 1]} \left( {\mathop \sum \limits_{j = k}^{n} d_{[j]} - d_{[k + 1]} } \right) + l_{[k]} \left( {\mathop \sum \limits_{j = k}^{n} d_{[j]} - d_{[k + 1]} - d_{[k]} } \right)} \right) \\ & \quad = h_{F} \left( {l_{[k]} d_{[k + 1]} - l_{[k + 1]} d_{[k]} } \right) = h_{F} l_{[k]} l_{[k + 1]} \left( {\frac{{d_{[k + 1]} }}{{l_{[k + 1]} }} - \frac{{d_{[k]} }}{{l_{[k]} }}} \right). \\ \end{aligned}$$

(16)

From Eq. (16), we can infer that $TRC\left( {\alpha ,T\left( \alpha \right),Z_{a} } \right)_{{M_{1} }} \ge TRC\left( {\alpha ,T\left( \alpha \right),Z_{b} } \right)_{{M_{1} }}$ if $\frac{{d_{[k]} }}{{l_{[k]} }} \ge \frac{{d_{[k + 1]} }}{{l_{[k + 1]} }}$. As a result, without loss of generality, the delivery sequence Z should be established in such a way that the following condition is satisfied:

$$\frac{{d_{\left[ i \right]} }}{{l_{\left[ i \right]} }} \ge \frac{{d_{{\left[ {i + 1} \right]}} }}{{l_{{\left[ {i + 1} \right]}} }}, \quad {\text{where}}\,\,i = 1, 2, \ldots , n - 1.$$

(17)

Appendix 3

From Eqs. (5a) and (5b), we calculate that ratio of α⁰ and α^b as follows:

$$\frac{{\alpha^{0} }}{{\alpha^{b} }} = \frac{{\left( {\frac{{h_{R} }}{{\left( {s - 1} \right)c_{\alpha } }}\left( {1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } T}}} \right)} \right)^{\frac{1}{s}} }}{{\left( {\frac{{2h_{R} }}{{\left( {1 - s} \right)\left( {s - 2} \right)c_{\alpha } }}\left( {1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } T}}} \right)} \right)^{\frac{1}{s}} }} = \left( {\frac{{\left( {1 - s} \right)\left( {s - 2} \right)}}{{2\left( {s - 1} \right)}}} \right)^{\frac{1}{s}} = \left( {1 - \frac{s}{2}} \right)^{\frac{1}{s}} .$$

(18)

Equation (18) shows that $\frac{{\alpha^{0} }}{{\alpha^{b} }} < 1$ or, equivalently, $\alpha^{0} < \alpha^{b}$ since $\left( {1 - \frac{s}{2}} \right) < 1$ if $0 < s < 2$. Thus, if a⁰ is a valid stationary point, then it is always smaller than α^b, which is the point where the convex region of the objective function ends and the concave region starts.

Appendix 4

This appendix illustrates the typical patterns of both the first and second partial derivative of $TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }}$ with respect to α for Cases 1.2 and 2.1 (cf. Figs. 5, 6). In both figures, the solid line represents the value of $\frac{{\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{\partial \alpha }$, while the dotted line is used for $\frac{{\partial^{2} TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{{\partial \alpha^{2} }}$.

Fig. 5

Typical patterns of $\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} /\partial \alpha$ and $\partial^{2} TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} /\partial \alpha^{2}$ in Case 1.2. (h _R  = 4, $c_{\alpha } = 0.5$, d_max = 500, T = 0.3, $\sum\nolimits_{i = 1}^{n} d_{i} l_{i}$ = 120, s = 1.5)

Fig. 6

Typical patterns of $\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} /\partial \alpha$ and $\partial^{2} TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} /\partial \alpha^{2}$ in Case 2.1. (h _R  = 4, $c_{\alpha } = 0.5$, d_max = 500, T = 0.3, $\sum\nolimits_{i = 1}^{n} d_{i} l_{i}$ = 250, s = 0.5)

We first consider Case 1.2 where $T > \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } }}$ and $1 < s < 2.$ As can be seen in Fig. 5, $TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }}$ is a convex function if α ≤ α^b, while it is a concave function in case α > α^b. Thus, the container capacity should be set to α⁰, as it is a unique value satisfying the first-order optimality condition, i.e., $\frac{{\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{\partial \alpha } = 0$, and since the value of the objective function increases for values of α that are larger than α⁰.

The pattern of $TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }}$ is reversed in Case 2.1 where $T < \frac{{\mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{{d_{{\rm max} } }}$ and $s < 1$. In other words, it is a concave function when $\alpha \le \alpha^{b}$, while it is a convex function when $\alpha > \alpha^{b}$. Thus, the container capacity should be set to one of the two boundary values, i.e., α_min and α_max, since α⁰ is a unique value satisfying the first-order optimality condition, i.e., $\frac{{\partial TRC\left( {\alpha ,T|Z} \right)_{{M_{1} }} }}{\partial \alpha } = 0$, in a concave region.

Appendix 5

To calculate the average inventory at the supplier, we first calculate the cumulative production quantity of a cycle and reduce it by the cumulative quantity shipped to the buyers (see Fig. 7; cf. [20] for a similar approach).

Fig. 7

Cumulative production and shipment quantity of a supplier for five shipments

From Fig. 7, the average inventory level of the vendor can be calculated as follows:

$${\text{Avg}} . {\text{ Area}}_{F} = \frac{{\left( \frac{1}{2} \right)\left( \frac{Q}{P} \right)Q + \left( {\frac{{q_{\left[ 1 \right]} }}{P} + \mathop \sum \nolimits_{i = 1}^{n - 1} l_{\left[ i \right]} - \frac{Q}{P}} \right)Q - \mathop \sum \nolimits_{i = 1}^{n - 1} l_{\left[ i \right]} \mathop \sum \nolimits_{j = 1}^{i} q_{\left[ j \right]} }}{T}.$$

(19)

Simplification leads to

$${\text{Avg}} . {\text{ Area}}_{F} = \frac{{d\left( {2d_{[1]} - d} \right)}}{2P}T + \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{\left[ j \right]} .$$

(20)

The total relevant cost of the system can now be calculated as

$$\begin{aligned} TRC\left( {\alpha ,T,Z} \right)_{{M_{2} }} & = \frac{{\left( {S + \mathop \sum \nolimits_{i = 1}^{n} A_{i} - h_{R} \mathop \sum \nolimits_{i = 1}^{n} r_{i} l_{i} } \right)}}{T} + \left( {\mathop \sum \limits_{i = 1}^{n} \frac{{h_{i} d_{i} }}{2} + \frac{{h_{F} d\left( {2d_{[1]} - d} \right)}}{2P}} \right)T \\ & \quad + h_{R} r_{{\rm max} } + c_{\alpha } \alpha^{s} r_{{\rm max} } + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{\left[ j \right]} . \\ \end{aligned}$$

(21)

Simplification leads to the expression given in Eq. (9). To make sure that the inventory level of the supplier does not become negative at any point in time, the following two feasibility conditions have to be satisfied:

$$\left( {\frac{{q_{[1]} }}{P} + \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} } \right) - \frac{Q}{P} \ge 0.$$

(22)

$$l_{[n]} \le \frac{{q_{[1]} }}{P}.$$

(23)

Simplifying and combining both conditions leads to the one presented in Eq. (10).

Appendix 6

In the non-coordinated case, we assume that the supplier determines the production–delivery policy solely based on its own costs without considering the retailers’ cost information. From Eqs. (3) and (8), the supplier’s cost functions for two distinctive shipment patterns, i.e., $SRC\left( {\alpha ,T,Z} \right)_{{N_{1} }}$ and $SRC\left( {\alpha ,T,Z} \right)_{{N_{2} }}$, are derived as seen in Eqs. (24) and (26), respectively. The corresponding optimal policy can be derived using the proposed solution procedure.

6.1 (Non-coordinated model for late shipments)

$$SRC\left( {\alpha ,T,Z} \right)_{{N_{1} }} = \frac{S}{T} + \left( {\frac{{h_{F} d^{2} }}{2p} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } } \right)T - \frac{{h_{R} \mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{\alpha } + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{[j]} .$$

(24)

$$T^{*} \left( {\alpha |Z} \right) = {\rm min} \left( {T^{0} \left( {\alpha |Z} \right),T_{{\rm min} } } \right) ,\quad {\text{where}}\quad T^{0} \left( {\alpha |Z} \right) = \sqrt {\frac{S}{{\frac{{h_{F} d^{2} }}{2p} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } }}} .$$

(25)

6.2 (Non-coordinated model for early shipments)

$$SRC\left( {\alpha ,T,Z} \right)_{{N_{2} }} = \frac{S}{T} + \left( {\frac{{h_{F} d\left( {2d_{[1]} - d} \right)}}{2P} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } } \right)T - \frac{{h_{R} \mathop \sum \nolimits_{i = 1}^{n} d_{i} l_{i} }}{\alpha } + h_{F} \mathop \sum \limits_{i = 1}^{n - 1} l_{[i]} \mathop \sum \limits_{j = i + 1}^{n} d_{\left[ j \right]} .$$

(26)

$$T^{*} \left( {\alpha |Z} \right) = {\rm min} \left( {{\rm max} \left( {T^{0} \left( {\alpha |Z} \right),T_{{\rm min} } } \right),T_{{\rm max} } } \right),\quad {\text{where}} \,T^{0} \left( {\alpha |Z} \right) = \sqrt {\frac{S}{{\frac{{h_{F} d\left( {2d_{\left[ 1 \right]} - d} \right)}}{2P} + \left( {\frac{{h_{R} }}{\alpha } + c_{\alpha } \alpha^{s - 1} } \right)d_{{\rm max} } }}} .$$

(27)