Sharp bounds on distribution functions and expectations of mixtures of ordered families of distributions

Abstract

We compare two mixtures of arbitrary collection of stochastically ordered distribution functions with respect to fixed mixing distributions. Under the assumption that the first mixture distribution is known, we establish optimal lower and upper bounds on the latter mixture distribution function and present single families of ordered distributions which attain the bounds uniformly at all real arguments. Furthermore, we determine sharp upper and lower bounds on the differences between the expectations of the mixtures expressed in various scale units. General results are illustrated by several examples.

1 Introduction

Let $\{F_\theta \}_{\theta \in {\mathbb {R}}}$ be an arbitrary family of stochastically ordered distribution functions, i.e., ones that satisfy

$$\begin{aligned} \theta _1 < \theta _2 \Rightarrow F_{\theta _1}(x) \ge F_{\theta _2}(x), \quad x \in {\mathbb {R}}. \end{aligned}$$

(1.1)

We assume that the family is not known. We further introduce two distribution functions S and T which are assumed to be known. We do not impose any restrictions on them. They may have discrete and/or continuous components, and supports concentrated on possibly partially or even fully different subsets of the real line. The purpose of the paper is to compare the mixture distribution functions

$$\begin{aligned} G(x)= & {} \int _{{\mathbb {R}}} F_\theta (x) S(\mathrm{d}\theta ), \end{aligned}$$

(1.2)

$$\begin{aligned} H(x)= & {} \int _{{\mathbb {R}}} F_\theta (x) T(\mathrm{d}\theta ), \end{aligned}$$

(1.3)

and their expectations.

Our model is motivated by nonparametric Bayes and regression ideas. The relation between the predictor $\theta$ and random response with distribution function $F_\theta$ is completely unknown except for a frequently natural and practically justified premise that the greater value of predictor results in a (stochastically) greater response. We investigate consequences of various choices of prior S and T for the wide nonparametric response model restricted merely by the above order constraints. Classic Bayes procedures are focused on identifying the predictor value managing a single random experiment. Our approach is global: we analyze the final consequences of random choice of predictor, and random response to the selected predictor. This corresponds to the situation of multiple repetitions of the experiment where various values of predictors are chosen according to the prior selection rule.

Precisely, in Sect. 2 we determine sharp lower and upper bounds on distribution functions (1.3) under the constraint that condition (1.2) is satisfied for an arbitrarily fixed G. The lower and upper bounds constitute proper distribution functions iff the mixing distribution function T does not have a positive mass right and left, respectively, to the support of S. We also show that the bounds are attained uniformly for any G, i.e., there exist single families $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ and $\{{\overline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ such that (1.2) holds, and the lower and upper bounds on (1.3) are attained by $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ and $\{{\overline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$, respectively, for every real argument x. In Sect. 3, we determine the greatest possible lower and upper deviations of ${\mathbb {E}}Y = \int _{{\mathbb {R}}}x H(\mathrm{d}x)$ from ${\mathbb {E}}X = \int _{{\mathbb {R}}}x G(\mathrm{d}x)$ (cf (1.2) and (1.3)), measured in various scale units $({\mathbb {E}}|X- {\mathbb {E}}X|^p)^{1/p}= \left( \int _{{\mathbb {R}}}|x-{\mathbb {E}}X|^p G(\mathrm{d}x)\right) ^{1/p}$, $p \ge 1$, based on central absolute moments of (1.2). We illustrate theoretical results by a number of examples in Sect. 4. Section 5 is devoted to the proof of Theorem 1 of Sect. 2 that is the basic result of the paper providing the tools for establishing the expectation bounds of Sect. 3.

Mixture models have multiple applications in probability and statistics. It was shown in a review paper of Karlis and Xekalaki (2003) that they are exploited in data modeling, discriminant and cluster analysis, outlier and robustness studies, analysis of variance, random effects and related models, factor analysis, and latent structure models, random variable generation, and approximation of distributions. Here we merely mention several nonparametric Bayesian inference and regression analysis applications. One of the pioneering works on nonparametric Bayesian estimation methods was that of Ferguson (1973) who provided Bayes estimates of the response distribution function and several its functionals under the Dirichlet process prior. Ghosh and Mukherjee (2005) presented a sequential version of the distribution function estimate. Susarla and Ryzin (1978), Tiwari and Zalkikar (1990), Gasparini (1996), and Zhou (2004) determined nonparametric Bayes estimators of distribution function under various censoring schemes. Sethuraman and Hollander (2009) estimated the nominal lifetime distribution of an unit exposed to various repair treatments. Hansen and Lauritzen (2002) proposed a method of Bayesian estimation of arbitrary concave distribution function when the prior is a proper mixture of Dirichlet processes. For the Bayesian density estimation, we refer to Escobar and West (1995) and Vieira et al. (2015), whereas the hazard rate function was treated by McKeague and Tighiouart (2002).

From the vast nonparametric Bayesian regression literature, we mention only the following. Choi (2008) studied convergence of posterior distributions when the response–predictor relation was modeled by mixtures of parametric densities, and a sieve prior was assumed. Chung and Dunson (2009) estimated the conditional response distribution and identified significant predictors under the assumption of probit stick-breaking process as a prior. Zhu and Dunson (2013) used nested Gaussian processes as locally adaptive priors for the regression model. Jo et al. (2016) considered quantile regression problems with the Dirichlet process mixture modeling the error distribution.

A small proportion of nonparametric Bayes research is devoted to order restricted inference. Assuming restricted dependent Dirichlet prior for a collection of partially ordered distributions, Dunson and Peddada (2008) tested equalities in the homogenous groups and estimated group-specific distributions. Yang et al. (2011) developed posterior computations for stochastically ordered latent class model based on the nested Dirichlet process prior. Nashimoto and Wright (2007, 2008) performed Bayesian multiple comparisons for ordered medians and means, respectively. The model of stochastically ordered mixtures presented here was earlier examined by Miziuła (2017) who established tight lower and upper bounds on the ratios of various dispersion measures of mixtures. Some similarities to our approach can be also found in Robertson and Wright (1982) where lower and upper bounds on mixtures of stochastically ordered Chi-squared distributions useful in testing homogeneity of normal means against their ordering were established.

2 Distribution functions of mixtures

The main result of this section is following.

Theorem 1

Let S, T, and G be fixed distribution functions on ${\mathbb {R}}$. Then for every family $\{F_\theta \}_{\theta \in {\mathbb {R}}}$ of stochastically ordered distribution functions (cf (1.1)) satisfying (1.2), the following inequalities hold

$$\begin{aligned} {\underline{H}}(G(x)) \le \int _{{\mathbb {R}}} F_\theta (x) T(\mathrm{d}\theta ) \le {\overline{H}}(G(x)), \quad x \in {\mathbb {R}}, \end{aligned}$$

(2.1)

where ${\underline{H}}, {\overline{H}}:[0,1] \mapsto [0,1]$ are the greatest convex minorant and the smallest concave majorant, respectively, of the set

$$\begin{aligned} {\mathcal {U}}= {\mathcal {U}}(S,T) = \{ (u,v)=(S(\theta ), T(\theta )): \; \theta \in {\mathbb {R}} \}. \end{aligned}$$

(2.2)

Moreover, the bounds in (2.1) are optimal and uniformly attainable which means that there exist stochastically ordered families $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ and $\{{\overline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ satisfying (1.2) such that for every real x yields

$$\begin{aligned} {\underline{H}}(G(x))&= \displaystyle \int _{{\mathbb {R}}} {\underline{F}}_\theta (x) T(\mathrm{d}\theta ), \\ {\overline{H}}(G(x))&= \displaystyle \int _{{\mathbb {R}}} {\overline{F}}_\theta (x) T(\mathrm{d}\theta ).\nonumber \end{aligned}$$

(2.3)

Remark 1

The set of stochastically ordered families satisfying (1.2) is non-empty. A trivial example is one-element family $\{ G \}_{\theta \in {\mathbb {R}}}$.

Remark 2

Set (2.2) is certainly a subset of the standard unit square $[0,1]^2$. It only contains ordered planar points which means that for every $(u_1,v_1),(u_2,v_2) \in {\mathcal {U}}$, inequality $u_1\le (\ge ,\;\mathrm {resp.})\;u_2$ implies the same relation between $v_1$ and $v_2$. Points (0, 0) and (1, 1) belong to ${\mathcal {U}}(S,T)$ iff both S and T have left and right bounded supports, respectively.

Besides, (2.2) may have very different forms for various S and T. Note first that since S and T are arbitrary, and we can interchange their roles. Except for given ${\mathcal {U}}(S,T)$ we also consider ${\mathcal {U}}(T,S)$ which is a symmetric transformation of ${\mathcal {U}}(S,T)$ about the diagonal $u=v$.

In the simplest case, when both S and T are continuous, (2.2) is represented by a single curve joining (0, 0) and (1, 1). It does not necessarily contain the end-points. The curve may contain horizontal line segments if S is increasing on some interval, and T is constant there. By the symmetry property mentioned above, vertical line segments are possible as well.

Another simple image set (2.2) arises when S and T are discrete. It consists of separate points. Notice that some of them may lie on some horizontal (or vertical) lines. If S is continuous and T is discrete, then ${\mathcal {U}}(S,T)$ consists of horizontal line segments. Sometimes the set is identical with the graph of non-decreasing right-continuous stepwise function which means that the steps have left end-points, and to not have the right ones. However, if S is constant on some left neighborhood of a jump of T, then the right end-point belongs to the line segment as well. Clearly, under the assumptions ${\mathcal {U}}(T,S)$ is built of vertical intervals.

After analyzing these simple cases, we are prepared for examining general S and T, possibly possessing some continuity intervals, and some discontinuities. Set (2.2) consists of at most countably many pieces. For each pair of pieces, one is located right and above the other. Only one coordinate of the left lower end-point of the former piece may be equal to the respective coordinate of the right upper end-point of the latter one. The pieces of (2.2) are either curves or separate points. The curves may contain horizontally and vertically oriented line segments as well as some their pieces can represent the graphs of strictly increasing functions. Each curve contains the point with minimal values of both coordinates, but it does not necessarily contain the right upper end-point.

Remark 3

The points of the graphs of the greatest convex minorant and the smallest concave majorant of (2.2) either coincide with the points of the set, or belong to straight line segments joining the elements of the set (more precisely, the limiting values of the right upper ends of the set pieces may also serve as the left and right ends of the line segments). By definition of ${\mathcal {U}}(S,T)$, the greatest convex minorant and the smallest concave majorant are non-decreasing functions. They are obviously continuous as well. Accordingly, compositions ${\underline{H}}\circ G$ and ${\overline{H}}\circ G$ are well-defined functions on the whole real axis, non-decreasing, right-continuous, and have all values in [0, 1].

Their actual image sets can be smaller, though. We explain when it occurs with use of a natural notion of ordering intervals which we further often use in the proof of Theorem 1. We say that interval $\Theta _1$ precedes interval $\Theta _2$, and write $\Theta _1 \prec \Theta _2$ iff for every $\theta _1 \in \Theta _1$ and $\theta _2 \in \Theta _2$ we have $\theta _1 < \theta _2$. We admit that the intervals have or do not have their left and right end-points. Accordingly, ${\underline{H}}\circ G$ is a distribution function iff

$$\begin{aligned} \forall \, \Theta _1 \prec \Theta _2 \quad S(\Theta _1)=1 \;\Rightarrow \;T(\Theta _2)=0. \end{aligned}$$

(2.4)

(for simplicity of notation, we use the same symbol for the distribution function and respective probability distribution). Clearly, ${\underline{H}}\circ G$ is not a proper distribution function iff

$$\begin{aligned} \exists \, \Theta _1 \prec \Theta _2 \quad S(\Theta _1)=1, \; T(\Theta _2)>0. \end{aligned}$$

(2.5)

Then

$$\begin{aligned} 1> {\overline{u}}= {\overline{u}}(S,T)= 1- \max \{ T(\Theta _2): \;\Theta _2 \succ \Theta _1,\; S(\Theta _1)=1 \}. \end{aligned}$$

(2.6)

is the supremum point of ${\underline{H}}\circ G({\mathbb {R}})$. It means that ${\underline{H}}\circ G$ is not a distribution function when T has a positive probability mass right to the support of S. This may even happen when the support of T is contained in that of S, but they have a joint right support end-point, at which T has an atom, and S has not. Formally we admit the situation that ${\underline{u}}(S,T)= 0$ if the whole mass of T is located right to the mass of S, and then ${\underline{H}}\circ G$ simply vanishes. Analogously, ${\overline{H}}\circ G$ is a proper distribution function iff

$$\begin{aligned} \forall \, \Theta _1 \prec \Theta _2 \quad S(\Theta _2)=1 \;\Rightarrow \;T(\Theta _1)=0. \end{aligned}$$

(2.7)

In the general case, $\inf {\overline{H}}\circ G({\mathbb {R}})= {\underline{u}}\ge 0$ where

$$\begin{aligned} {\underline{u}}= \max \{ T(\Theta _1): \;\Theta _1 \prec \Theta _2,\; S(\Theta _2)=1 \}. \end{aligned}$$

It is clear that ${\underline{u}} \ge {\overline{u}}$.

Remark 4

Observe that the inverses

$$\begin{aligned} \underline{{\underline{H}}}(u)= \left\{ \begin{array}{ll} 0, &{}\quad 0 \le u \le {\overline{u}}, \\ {\overline{H}}^{-1} (u), &{}\quad {\overline{u}} \le u \le 1, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \overline{{\overline{H}}}(u)= \left\{ \begin{array}{ll} {\underline{H}}^{-1} (u), &{}\quad 0 \le u \le {\underline{u}}, \\ 1, &{}\quad {\underline{u}} \le u \le 1, \end{array} \right. \end{aligned}$$

are the greatest convex minorant and the smallest concave majorant, respectively, of the set ${\mathcal {U}}(T,S)$ which are exploited in minimizing and maximizing mixture distribution function $\int _{{\mathbb {R}}} F_{\theta }(x) S(\mathrm{d}\theta )$ under restriction on fixed form of $\int _{{\mathbb {R}}} F_{\theta }(x) T(\mathrm{d}\theta )$.

The proofs of the lower and upper bounds, and their attainability are rather long, but similar. Therefore in the proof presented in Sect. 5, we restrict ourselves to the lower bound case. Families $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ and $\{{\overline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ which attain the bounds in (2.1) strongly depend on the particular shape of set (2.2), and resulting forms of the greatest convex minorant and the smallest concave majorant. It is impossible to describe them in a concise form for general S and T (dependence on G is much simpler here) in the statement of Theorem 1. Precise construction of $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ is presented in the proof of Theorem 1. Construction of $\{{\overline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ is analogous to that of $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$, and it not presented there.

3 Expectations of mixtures

In this section we examine variations of the expectations of mixtures under stochastic ordering of mixed distributions. Suppose that we consider a mixture of arbitrary unknown family of ordered distribution functions, and the actual mixing distribution is S. The resulting random variable X has an unknown distribution function (1.2). However, we assume that the mixing distribution is T, different from S. This generates a random variable Y with different distribution function (1.3) and expectation ${\mathbb {E}}Y$. Our purpose is to evaluate the maximal possible differences between the assumed and actual expectations of mixtures ${\mathbb {E}}Y-{\mathbb {E}}X$. This is measured in various scale units $\sigma _p= ({\mathbb {E}}|X-{\mathbb {E}}X|^p)^{1/p}$, $p \ge 1$, generated by the central absolute moments of the actual mixture variable X. The bounds depend merely on the mixing distributions S and T, and on the parameter p of the measurement units $\sigma _p$. They are valid for all possible $\{F_\theta \}_{\theta \in {\mathbb {R}}}$, and resulting mixture distributions G and H. The only restriction is that X has a finite pth raw moment ${\mathbb {E}}|X|^p$ of chosen order $p \ge 1$, and Y has a finite expectation. Similarly, under condition that actual mixture variable X has a bounded support, we determine upper and lower bounds on ${\mathbb {E}}Y-{\mathbb {E}}X$ gauged in the scale units $\sigma _{\infty } = \mathrm {ess} \sup |X-{\mathbb {E}}X| = \sup _{\{0<x <1 \}} |G^{-1}(x)- {\mathbb {E}}X|$.

First we exclude the possibilities for which we obtain trivial infinite bounds on ${\mathbb {E}}Y-{\mathbb {E}}X$, independently of the choice of the scale units. Assume first that S and T are such that respective ${\underline{H}}([0,1]) = [0,{\overline{u}}] \subsetneqq [0,1]$, i.e., condition (2.5) holds. Then clearly one can find the partition $\Theta _1$, $\Theta _2$ of ${\mathbb {R}}$ such that (2.5) is satisfied with $T(\Theta _2)= 1-{\overline{u}}$. Take the family of distributions

$$\begin{aligned} F_\theta = \left\{ \begin{array}{ll} F_U, &{}\quad \theta \in \Theta _1, \\ F_P, &{}\quad \theta \in \Theta _2, \end{array} \right. \end{aligned}$$

where $F_U(x)=x$, $0 \le x \le 1$, and $F_P(x) = 1 - \frac{1}{x}$, $x \ge 1$, are the standard uniform and Pareto distributions with shape parameter 1, respectively. Then obviously $G=F_U$, $H=(1-{\overline{u}})F_U+{\overline{u}} F_P$, and so ${\mathbb {E}}X= \frac{1}{2}$, $\frac{1}{4} \le \sigma _p \le \frac{1}{2}$ for all $1 \le p \le +\infty$ whereas ${\mathbb {E}}Y= + \infty$. Similarly, contradicting (2.7), we are able to choose an ordered family such that its mixtures with respect to S and T have bounded support, and expectation $-\infty$, respectively. Therefore assumptions (2.4) and (2.7) are necessary for getting nontrivial finite upper and lower bounds on ${\mathbb {E}}Y-{\mathbb {E}}X$.

Other extremities may occur when S and T are stochastically ordered. If $S(\theta ) \ge T(\theta )$, $\theta \in {\mathbb {R}}$, then all the points of (2.2) lie either above or on the diagonal $\{ (u,u):\; 0 \le u \le 1 \}$ of the unit square. If we additionally assume (2.4), we obtain ${\underline{H}}(u)=u$, $0 \le u \le 1$. By Theorem 1, we get $H(x) \ge G(x)$, $x \in {\mathbb {R}}$, and ${\mathbb {E}}Y \le {\mathbb {E}}X$ for an arbitrary choice of ordered $\{ F_\theta \}_{\theta \in {\mathbb {R}}}$ for which the expectations exist. Similarly, assumptions $S \le T$ and (2.7) imply ${\mathbb {E}}Y \ge {\mathbb {E}}X$ for any $\{ F_\theta \}_{\theta \in {\mathbb {R}}}$. Determination of the nonpositive upper bounds and nonnegative lower ones for $({\mathbb {E}}Y - {\mathbb {E}}X)/\sigma _p$, $1 \le p \le + \infty$, when $S \ge T$ and $S \le T$, respectively, needs more subtle tools than these used below, and will be treated elsewhere.

Now we present strictly positive upper bounds and strictly negative lower bounds on $({\mathbb {E}}Y - {\mathbb {E}}X)/\sigma _p$ for $1<p <\infty$, $p=1$ and $p=+\infty$ in Propositions 1, 2, and 3, respectively. Due to its importance and relative simplicity, case $p=2$ is especially distinguished in Corollary 1. The bounds depend on the mixing distributions S and T, and the scale unit parameter p, and all of them are optimal. We describe conditions of their attainability by specifying mixture distribution $G=G(S,T,p)$ (see (1.2)). Construction of the families of mixing distributions $\{{\underline{F}}_{\theta }\}_{\theta \in {\mathbb {R}}}$ and $\{{\overline{F}}_{\theta }\}_{\theta \in {\mathbb {R}}}$ providing stochastically minimal and maximal mixture distribution H (and, in consequence, maximal and minimal expectations ${\mathbb {E}}Y$, respectively) for given S, T, and $G=G(S,T,p)$ are described in the proof of Theorem 1.

Proposition 1

Let X and Y be random variables with distribution functions which are the mixtures of some stochastically ordered families of distributions $\{F_{\theta }\}_{\theta \in {\mathbb {R}}}$ with respect to fixed distribution functions S and T, respectively. Assume that X has a finite pth moment for some fixed $1< p < \infty$.

• (i) Suppose that $S \ngeq T$ satisfy (2.4), and denote by ${\underline{h}}$ the right-continuous version of the derivative of the greatest convex minorant of set ${\mathcal {U}}(S,T)$ defined in (2.2). If $\int _0^1 {\underline{h}}^{p/(p-1)}(u) \,du$ is finite, then for all mixture distribution functions (1.2) for which ${\mathbb {E}}|X|^p< \infty$ we have

  $$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{({\mathbb {E}}|X-{\mathbb {E}}X|^p)^{1/p}} \le B_p(S,T) = \left( \int _0^1 |{\underline{h}}(u)-C_p|^{p/(p-1)}\mathrm{d}u \right) ^{(p-1)/p}, \nonumber \\ \end{aligned}$$

  (3.1)

  where ${\underline{h}}(0)< C_p < {\underline{h}}(1)$ uniquely solves the equation

  $$\begin{aligned} \int _{\{{\underline{h}}(u)<c\}} [c-{\underline{h}}(u)]^{1/(p-1)} \mathrm{d}u = \int _{\{{\underline{h}}(u)>c\}} [{\underline{h}}(u)-c]^{1/(p-1)} \mathrm{d}u. \end{aligned}$$

  (3.2)

  The equality in (3.1) is attained if (1.2) has the right-continuous quantile function satisfying

  $$\begin{aligned} \frac{G^{-1}(u)-\mu }{\sigma _p} = \left| \frac{{\underline{h}}(u)-C_p}{B_p(S,T)} \right| ^{1/(p-1)} \times \mathrm {sgn}\; \{ {\underline{h}}(u)-C_p\}, \quad 0< u < 1, \nonumber \\ \end{aligned}$$

  (3.3)

  where $\mu \in {\mathbb {R}}$ and $\sigma _p^p\in {\mathbb {R}}_+$ denote arbitrarily chosen values of expectation and pth absolute central moment of G, respectively.

• (ii) Let $S \nleq T$ satisfy (2.7), and ${\overline{h}}$ denote the right derivative of the smallest concave majorant of (2.2). If $\int _0^1 {\overline{h}}^{p/(p-1)}(u) \,\mathrm{d}u< \infty$, then for all mixture distributions (1.2) with finite pth moment yields

  $$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{({\mathbb {E}}|X-{\mathbb {E}}X|^p)^{1/p}} \ge -b_p(S,T) = - \left( \int _0^1 |{\overline{h}}(u)-c_p|^{p/(p-1)}\mathrm{d}u \right) ^{(p-1)/p}, \end{aligned}$$

  (3.4)

  where ${\overline{h}}(0)> c_p > {\overline{h}}(1)$ is determined by Eq. (3.2) with ${\underline{h}}$ replaced by ${\overline{h}}$. The equality in (3.4) is attained by (1.2) with the quantile function

  $$\begin{aligned} \frac{G^{-1}(u)-\mu }{\sigma _p} = \left| \frac{{\overline{h}}(u)-c_p}{b_p(S,T)} \right| ^{1/(p-1)} \times \mathrm {sgn}\; \{ c_p-{\overline{h}}(u)\}, \quad 0< u < 1, \end{aligned}$$

  and $\mu$ and $\sigma _p^p$ denoting arbitrarily chosen expectation and pth absolute central moments of G.

Proof

We prove statement (i). Note first that by definition ${\underline{h}}$ is well-defined nonnegative, non-decreasing and right continuous function. Assumption $\int _0^1 {\underline{h}}^{p/(p-1)}(u) \,\mathrm{d}u< \infty$ implies that the left hand-side of (3.2) is a continuous strictly decreasing function of c ranging from $\int _0^1 {\underline{h}}^{1/(p-1)}(u) \,\mathrm{d}u$ at 0 to 0 as $c \nearrow {\underline{h}}(1)$ even if it is infinite. Similarly, the right-hand side of (3.2) continuously increases from 0 to $\int _0^1 {\underline{h}}^{1/(p-1)}(u) \,\mathrm{d}u$ as c varies over the same range.

We can write

$$\begin{aligned} \mu= & {} {\mathbb {E}}X = \int _{{\mathbb {R}}}x\, G(\mathrm{d}x) = \int _0^1 G^{-1}(u)\mathrm{d}u, \nonumber \\ \sigma _p^p= & {} {\mathbb {E}}|X-\mu |^p = \int _0^1 |G^{-1}(u)-\mu |^p \mathrm{d}u \end{aligned}$$

(3.5)

whereas owing to Theorem 1

$$\begin{aligned} {\mathbb {E}}Y= & {} \int _{\mathbb {R}}x H(\mathrm{d}x) \le \int _{{\mathbb {R}}} x {\underline{H}}(G(\mathrm{d}x)) \\= & {} \int _0^1 G^{-1}(u) {\underline{H}}(\mathrm{d}u) = \int _0^1 G^{-1}(u) {\underline{h}}(u)\mathrm{d}u. \end{aligned}$$

Since we also have $\mu = \mu {\underline{H}}(1) = \int _0^1 \mu {\underline{h}}(u) \mathrm{d}u$, the following yields

$$\begin{aligned} {\mathbb {E}}Y- {\mathbb {E}}X\le & {} \int _0^1 [G^{-1}(u)-\mu ] {\underline{h}}(u)\mathrm{d}u = \int _0^1 [G^{-1}(u)-\mu ][ {\underline{h}}(u)-C_p] \mathrm{d}u\\\le & {} \left( \int _0^1 |G^{-1}(u)-\mu |^p \mathrm{d}u\right) ^{1/p} \left( \int _0^1 | {\underline{h}}(u)-C_p|^{p/(p-1)} du\right) ^{(p-1)/p} \end{aligned}$$

which, due to (3.5), gives (3.1).

We obtain equality in the above Hölder inequality iff $\left| {\underline{h}}(u)-C_p \right| ^{1/(p-1)}\mathrm {sgn} \{ {\underline{h}}(u)-C_p\}$ and $G^{-1}(u)-\mu$ are proportional with a nonnegative proportionality factor which is fulfilled in (3.3). By (3.2), the right-hand side of (3.3) has zero Lebesgue integral over [0, 1] which guarantees that the expectation of G is equal to $\mu$. Moreover,

$$\begin{aligned} 1= \int _0^1 \left| \frac{{\underline{h}}(u)-C_p}{B_p(S,T)} \right| ^{p/(p-1)} \mathrm{d}u = \int _0^1 \frac{|G^{-1}(u)-\mu |^p}{\sigma _p^p} \mathrm{d}u, \end{aligned}$$

which means that the pth absolute central moment of G amounts to $\sigma _p^p$, as desired.

Similar proof of claim (ii) is left to the reader. $\square$

Remark 5

Assumption $\int _0^1 {\underline{h}}^{p/(p-1)}(u) \,\mathrm{d}u< \infty$ is necessary for finiteness of the upper bound in Proposition 1 even if (2.4) holds. Indeed, infiniteness of the integral implies that ${\underline{H}}$ is not linear an some left neighborhood $(1-\varepsilon ,1)$ of 1, and its graph coincides with a piece of set (2.2) there. This means that

$$\begin{aligned} \forall \,1-\varepsilon<u<1 \quad \{(u,{\underline{H}}(u))\} = \{ (S(\theta ), T(\theta )) : \theta \in \Theta ^u\} \end{aligned}$$

where $\{\Theta ^u\}_{1-\varepsilon<u<1}$ is a family of ordered intervals so that $1-\varepsilon<u_1<u_2<1$ implies $\Theta ^{u_1} \prec \Theta ^{u_2}$, and $\bigcup _{1-\varepsilon<u<1} \Theta ^u$ constitutes a single right-unbounded interval. From the proof of Theorem 1 we conclude that the family $\{ {\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ attaining uniformly the lower bound in (2.1) consists of degenerate distributions for all $\theta \in \bigcup _{1-\varepsilon<u<1} \Theta ^u$.

If we take $1-\varepsilon< u_1 <1$, and replace all the degenerate distribution functions ${\underline{F}}_\theta$, $\theta \in \bigcup _{u_1<u<1} \Theta ^u$, by a single distribution function

$$\begin{aligned} {\underline{F}}_{u_1}(x) = \left\{ \begin{array}{ll} 0, &{}\quad G(x) \le S(\theta _{u_1}), \\ \frac{G(x) - S(\theta _{u_1})}{1-S(\theta _{u_1})} &{}\quad S(\theta _{u_1}) \le G(x) \le 1, \end{array} \right. \end{aligned}$$

where $\theta _{u_1}$ is any element of $\Theta ^{u_1}$, we do not disturb ordering of the family, and the shape of ${\underline{H}}$ on $[0,u_1]$, and modify the latter into the linear function $\frac{1-{\underline{H}}(u_1)}{1-u_1} (u-u_1) + {\underline{H}}(u_1)$ on $(u_1,1]$. The resulting distribution function ${\underline{H}}_1$ preserves convexity, and its right derivative ${\underline{h}}_1$ is bounded. There exists a unique $C_{p,1}$ being the solution to (3.2) with ${\underline{h}}$ replaced by ${\underline{h}}_1$. For finite

$$\begin{aligned} B_{p,1}(S,T) = \left( \int _0^1 |{\underline{h}}_1(u)-C_{p,1}|^{p/(p-1)}\mathrm{d}u \right) ^{(p-1)/p} \end{aligned}$$

and $G_1$ satisfying

$$\begin{aligned} \frac{G^{-1}_1(u)-\mu }{\sigma _p} = \left| \frac{{\underline{h}}_1(u)-C_{p,1}}{B_{p,1}(S,T)} \right| ^{1/(p-1)} \times \mathrm {sgn}\; \{ {\underline{h}}_1(u)-C_{p,1}\}, \quad 0< u < 1, \end{aligned}$$

we get

$$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{({\mathbb {E}}|X-{\mathbb {E}}X|^p)^{1/p}} = B_{p,1}(S,T) \end{aligned}$$

where X and Y have distribution functions $G_1$ and ${\underline{H}}_1 \circ G_1$, respectively, arising by mixing ordered families of distribution functions with respect to S and T. We repeat the procedure for consecutive elements of increasing sequence $(u_k)_{k=1}^\infty$ tending to 1. Then bounded ${\underline{h}}_k$ tend increasingly to ${\underline{h}}$, and

$$\begin{aligned} \int _0^1 |{\underline{h}}_k(u)-c|^{p/(p-1)}\mathrm{d}u \rightarrow +\infty , \quad \mathrm {as}\;k \rightarrow +\infty , \end{aligned}$$

for arbitrary c, and for all $C_{p,k}$ in particular. This implies that the difference ${\mathbb {E}}Y - {\mathbb {E}}X$ measured in $\left( {\mathbb {E}}|X-{\mathbb {E}}X|^p\right) ^{1/p}$ units does not have a finite bound.

Analogously, we verify that under conditions (2.5) and $\int _0^1 {\overline{h}}^{p/(p-1)}(u) \,\mathrm{d}u= \infty$, the respective lower bound amounts to $-\,\infty$.

Corollary 1

Assume notation of Proposition 1, and specify $p=2$.

• (i) If (2.4), $S \ngeq T$, and $\int _0^1 {\underline{h}}^2(u)\mathrm{d}u < \infty$ hold, then

  $$\begin{aligned} \frac{{\mathbb {E}}Y - {\mathbb {E}}X}{\sqrt{{\mathbb {V}}ar\,X}} \le B_2(S,T) = \sqrt{\int _0^1 {\underline{h}}^2(u)\mathrm{d}u -1 }, \end{aligned}$$

  and equality is attained iff

  $$\begin{aligned} \frac{G^{-1}(u) -\mu }{\sigma _2} = \frac{{\underline{h}}(u)-1}{B_2(S,T)}, \quad 0< u < 1. \end{aligned}$$

• (ii) Under assumptions (2.7), $S\nleq T$, and $\int _0^1 {\overline{h}}^2(u)\mathrm{d}u < \infty$

  $$\begin{aligned} \frac{{\mathbb {E}}Y - {\mathbb {E}}X}{\sqrt{{\mathbb {V}}ar\,X}} \ge - b_2(S,T) =- \sqrt{\int _0^1 {\overline{h}}^2(u)\mathrm{d}u -1 }, \end{aligned}$$

  and equality is attained iff

  $$\begin{aligned} \frac{G^{-1}(u) -\mu }{\sigma _2} = \frac{1-{\overline{h}}(u)}{b_2(S,T)}, \quad 0< u < 1. \end{aligned}$$

An essential simplification in case $p=2$ follows from the fact that under the above assumptions we get $\int _0^1 {\underline{h}}(u)\mathrm{d}u = {\underline{H}}(1)-{\underline{H}}(0)= 1 = \int _0^1 {\overline{h}}(u)\mathrm{d}u = {\overline{H}}(1)-{\overline{H}}(0)$. This implies that $C_2=c_2=1$ then. Moreover, $\int _0^1 [{\underline{h}}(u)-1]^2\mathrm{d}u =\int _0^1 {\underline{h}}^2(u)\mathrm{d}u -1$, and the same equality holds for ${\overline{h}}$.

Proposition 2

Let X, Y, and ${\underline{h}}$, ${\overline{h}}$ be defined as in Proposition 1, and suppose that X has a finite mean.

• (i) If (2.4) holds, $S \ngeq T$, and ${\underline{h}}$ is bounded, then

  $$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \le \frac{{\underline{h}}(1)-{\underline{h}}(0)}{2}, \end{aligned}$$

  (3.6)

  where ${\underline{h}}(1)$ is the left derivative of ${\underline{H}}$ at 1. The equality is attained in the limit by the three-point distributions $G_\varepsilon$, where

  $$\begin{aligned} G_\varepsilon \left( \left\{ \mu \pm \frac{\sigma _1}{2\varepsilon } \right\} \right) = \varepsilon , \quad G_\varepsilon (\{ \mu \}) = 1-2\varepsilon , \end{aligned}$$

  as $\varepsilon \rightarrow 0$, and $\mu$ and $\sigma _1$ are arbitrarily chosen common values of the expectation and mean absolute deviation from the mean of all mixture distributions $G_\varepsilon$.

• (ii) Under (2.7), $S \nleq T$, and boundedness of ${\overline{h}}$, we have

  $$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \ge -\frac{{\overline{h}}(0)-{\overline{h}}(1)}{2}, \end{aligned}$$

  (3.7)

  with ${\overline{h}}(1)$ denoting the left derivative of ${\overline{H}}$ at 1. The bound is attained in the limit by the family of mixture distributions $\{G_\varepsilon \}_{0<\varepsilon <1/2}$ described in Proposition 2(i) as $\varepsilon \rightarrow 0$.

The difference between the attainability conditions in Proposition 2(i) and (ii) consists in different choice of mixed distribution functions $\{{\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ and $\{{\overline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ leading to different distributions ${\underline{H}}\circ G_\varepsilon$ and ${\overline{H}}\circ G_\varepsilon$ of Y.

Proof of Proposition 2

We focus on the proof of statement (i), because that of (ii) is similar, and we omit it here. We start with the relations

$$\begin{aligned} {\mathbb {E}}Y-{\mathbb {E}}X\le & {} \int _0^1 [G^{-1}(u) - \mu ] \left[ {\underline{h}}(u) - \frac{{\underline{h}}(0) + {\underline{h}}(1)}{2} \right] \mathrm{d}u \\\le & {} \sup _{0<u<1} \left| {\underline{h}}(u) - \frac{{\underline{h}}(0) + {\underline{h}}(1)}{2} \right| \int _0^1 |G^{-1}(u) - \mu |\mathrm{d}u \\= & {} \frac{{\underline{h}}(1) - {\underline{h}}(0)}{2} \sigma _1. \end{aligned}$$

If the distribution function of Y is $G_\varepsilon$, then

$$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\sigma _1}= & {} \frac{1}{2\varepsilon } \left[ \int _0^\varepsilon \left( \frac{{\underline{h}}(1) - {\underline{h}}(0)}{2}- {\underline{h}}(u) \right) \mathrm{d}u \right. \nonumber \\&\left. + \int _{1-\varepsilon }^1 \left( {\underline{h}}(u)-\frac{{\underline{h}}(1) - {\underline{h}}(0)}{2} \right) \mathrm{d}u \right] . \end{aligned}$$

(3.8)

Function ${\underline{h}}$ and its left continuous versions are monotone and continuous at 0 and 1, respectively. Accordingly, they tend to ${\underline{h}}(0)$ and ${\underline{h}}(1)$ uniformly over intervals $[0,\varepsilon ]$ and $[1-\varepsilon ,1]$ as $\varepsilon \rightarrow 0$. Therefore the right-hand side of (3.8) tends to $\frac{{\underline{h}}(1)-{\underline{h}}(0)}{2}$. $\square$

Obviously, the families of distributions described in Proposition 2 are not the only ones which attain the bounds in the limit. One can modify them in many ways without disturbing desired asymptotic properties. If ${\underline{h}}(u) = {\underline{h}}(0)$ and ${\underline{h}}(u) = {\underline{h}}(1)$ on some non-degenerate intervals $[0,u_0]$ and $[u_1,1]$, say, then bound (3.6) is attained non-asymptotically by a single family of ordered distributions. The necessary and sufficient conditions of attainability are then $G(\{\mu \})=1-u_0-u_1$ with

$$\begin{aligned} - \int _0^{u_0}[G^{-1}(u)-\mu ]\mathrm{d}u = \int _{u_1}^1[G^{-1}(u)-\mu ]\mathrm{d}u = \frac{\sigma _1}{2}. \end{aligned}$$

This happens when ${\underline{H}}$ is linear on some vicinities of 0 and 1. Accordingly, the condition for non-limit attainability of lower bound (3.7) is linearity of ${\overline{H}}$ about 0 and 1. It is worth pointing out that such behavior of ${\underline{H}}$ and ${\overline{H}}$ is not especially extraordinary, and occurs for a significant proportion of pairs S and T.

Observe that

$$\begin{aligned} {\underline{h}}(0) = \inf _{\theta \in {\mathbb {R}}} \frac{T(\theta )}{S(\theta )} \le 1 \le {\underline{h}}(1) = \sup _{\theta \in {\mathbb {R}}} \frac{1-T(\theta )}{1-S(\theta )} \end{aligned}$$

(3.9)

under condition (2.4), and

$$\begin{aligned} {\overline{h}}(0) = \sup _{\theta \in {\mathbb {R}}} \frac{T(\theta )}{S(\theta )} \ge 1 \ge {\overline{h}}(1) = \inf _{\theta \in {\mathbb {R}}} \frac{1-T(\theta )}{1-S(\theta )} \end{aligned}$$

(3.10)

when (2.7) holds. Miziuła and Solnický (2018, Theorem 1) (see Miziuła 2015, Section 2.3, for the proof completely different from the above) used these notions for presenting the inequalities

$$\begin{aligned} \min \left\{ 0, \frac{{\overline{h}}(1)-{\overline{h}}(0)}{2}\right\} \le \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \le \max \left\{ 0, \frac{{\underline{h}}(1)-{\underline{h}}(0)}{2} \right\} , \end{aligned}$$

when both (2.4) and (2.7) are assumed. In fact, the min, max, and zeros can be dropped, because ${\overline{h}}(1)-{\overline{h}}(0) \le 0 \le {\underline{h}}(1)-{\underline{h}}(0)$ due to (3.9) and (3.10).

Proposition 3

Take X, Y, and ${\underline{h}}$, ${\overline{h}}$ defined above and suppose that X has a bounded support.

• (i) If (2.4) holds, $S \ngeq T$, and $\int _0^1 {\underline{h}}(u)du < \infty$, we have

  $$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\mathrm {ess\,sup}|X-{\mathbb {E}}X|} \le 1- 2{\underline{H}}\left( \frac{1}{2} \right) . \end{aligned}$$

  (3.11)

  Furthermore, define

  $$\begin{aligned} 0 \le {\underline{\lambda }}_-= & {} \lambda \left( \left\{ {\underline{h}}(u)<{\underline{h}}\left( \frac{1}{2} \right) \right\} \right\} \le \frac{1}{2}, \end{aligned}$$

  (3.12)
  $$\begin{aligned} 0 \le {\underline{\lambda }}_+= & {} \lambda \left( \left\{ {\underline{h}}(u)>{\underline{h}}\left( \frac{1}{2} \right) \right\} \right\} \le \frac{1}{2}, \end{aligned}$$

  (3.13)

  for $\lambda (A)$ denoting the Lebesgue measure of measurable set $A\subset {\mathbb {R}}$. The equality in (3.11) is attained for (1.2) satisfying $G(\{ \mu - \sigma _\infty \}) = {\underline{\lambda }}_-$, $G(\{ \mu + \sigma _\infty \}) = {\underline{\lambda }}_+$, and

  $$\begin{aligned} \int _{\left\{ {\underline{h}}(u)={\underline{h}}\left( \frac{1}{2} \right) \right\} }[G^{-1}(u)-\mu ]\mathrm{d}u = \sigma _\infty ({\underline{\lambda }}_--{\underline{\lambda }}_+) \end{aligned}$$

  (3.14)

  with arbitrary $\mu \in {\mathbb {R}}$ and $\sigma _\infty \in {\mathbb {R}}_+$ serving as the mean and maximal absolute deviation from the mean, respectively, of distribution function G.

• (ii) Assume (2.7), $S \nleq T$, and $\int _0^1 {\overline{h}}(u)\mathrm{d}u < \infty$. It follows that

  $$\begin{aligned} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\mathrm {ess\,sup}|X-{\mathbb {E}}X|} \ge 1- 2{\overline{H}}\left( \frac{1}{2} \right) . \end{aligned}$$

  (3.15)

  Let ${\overline{\lambda }}_-$ and ${\overline{\lambda }}_+$ be defined as in (3.12) and (3.13), respectively, except for ${\underline{h}}$ replaced by ${\overline{h}}$. Bound (3.15) is attained if $G(\{ \mu - \sigma _\infty \}) = {\overline{\lambda }}_+$, $G(\{ \mu + \sigma _\infty \}) = {\overline{\lambda }}_-$, and

  $$\begin{aligned} \int _{\left\{ {\overline{h}}(u)={\overline{h}}\left( \frac{1}{2} \right) \right\} }[G^{-1}(u)-\mu ]\mathrm{d}u = \sigma _\infty ({\overline{\lambda }}_+-{\overline{\lambda }}_-) \end{aligned}$$

  with the above meaning of $\mu$ and $\sigma _\infty$.

Proof

• (i) We easily obtain (3.11), because

  $$\begin{aligned} {\mathbb {E}}Y-{\mathbb {E}}X\le & {} \int _0^1[G^{-1}(u)-\mu ]\left[ {\underline{h}}(u) - {\underline{h}} \left( \frac{1}{2} \right) \right] \mathrm{d}u \\\le & {} \sup _{0<u<1} |G^{-1}(u)-\mu | \int _0^1 \left| {\underline{h}}(u)-{\underline{h}}\left( \frac{1}{2} \right) \right| \mathrm{d}u \\= & {} \sigma _\infty \left[ 1- 2{\underline{H}}\left( \frac{1}{2} \right) \right] . \end{aligned}$$

  The former inequality follows from Theorem 1, and is valid and attainable for any G under appropriate choice of mixed distributions. The latter becomes the equality iff $G^{-1}(u)-\mu =-\, \sigma _\infty$ on $\left\{ {\underline{h}}(u)<{\underline{h}}\left( \frac{1}{2} \right) \right\}$ and $G^{-1}(u)-\mu =+\, \sigma _\infty$ on $\left\{ {\underline{h}}(u)>{\underline{h}}\left( \frac{1}{2} \right) \right\}$. If ${\underline{\lambda }}_-={\underline{\lambda }}_+=\frac{1}{2}$, and, in consequence, $\left\{ {\underline{h}}(u)={\underline{h}}\left( \frac{1}{2} \right) \right\}$ is either empty or a degenerate interval, the optimal G is the unique two-point symmetric distribution function supported on $\mu \pm \sigma _\infty$. Otherwise (3.14) is the only assumption necessary for fulfilling the first moment condition

  $$\begin{aligned} 0= \int _0^1 [G^{-1}(u) - \mu ]\mathrm{d}u = \sigma _\infty \lambda _{-} + \int _{\left\{ {\underline{h}}(u)={\underline{h}}\left( \frac{1}{2} \right) \right\} }[G^{-1}(u)-\mu ]\mathrm{d}x + \sigma _\infty {\underline{\lambda }}_+. \end{aligned}$$

• (ii) The proof is omitted due to its similarity to the above.

$\square$

If ${\underline{\lambda }}_-+{\underline{\lambda }}_+ <1$, the necessary condition (3.14) is in particular satisfied by two- or three-point distribution $G(\{ \mu - \sigma _\infty \}) = {\underline{\lambda }}_-$, $G(\{ \mu + \sigma _\infty \}) = {\underline{\lambda }}_+$, and $G\left( \left\{ \mu + \frac{{\underline{\lambda }}_--{\underline{\lambda }}_+}{1-{\underline{\lambda }}_- -{\underline{\lambda }}_+}\,\sigma _\infty \right\} \right) = 1- {\underline{\lambda }}_- -{\underline{\lambda }}_+$. We easily check that $-1 \le \frac{{\underline{\lambda }}_--{\underline{\lambda }}_+}{1-{\underline{\lambda }}_- -{\underline{\lambda }}_+} \le 1$ which assures that actually $\mathrm {ess\,sup}\,|X-{\mathbb {E}}X| = \sigma _\infty$. An analogous construction is possible in Proposition 3(ii).

Also, one can verify that dropping the assumptions on boundedness and integrability of ${\underline{h}}$ (and ${\overline{h}}$) in Propositions 2 and 3 implies that the respective upper (and lower) bounds are infinite. We finally point out that strengthening the assumptions on moments of X with mixture distribution G in Propositions 1–3 allows to relax respective conditions on integrability of powers of functions ${\underline{h}}$ and ${\overline{h}}$, and, in consequence, on moments of Y with distribution functions ${\underline{H}}\circ G$ and ${\overline{H}}\circ G$, respectively.

4 Examples

We first mention applications of our mixtures in the reliability theory. If a system is composed of n identical elements with arbitrary exchangeable joint lifetime distribution, then the single component lifetime is the discrete uniform mixture of n stochastically ordered component lifetime order statistics distributions, whereas the system lifetime is another convex combination of theses distributions whose probability vector, called the Samaniego signature, depends on the structure of the system (see Samaniego 1985; Navarro et al. 2008). These representations were used by Navarro and Rychlik (2007) for evaluating the distribution functions and expectations of system lifetimes by means of distribution functions and moments of component lifetimes. A similar idea can be used for calculating bounds on expectations of linear combinations of order statistics based on identically distributed samples (cf Rychlik 1993).

In the examples below, we restrict ourselves to calculating the sharp upper and lower bounds expressed with scale units with parameters $p=1$, 2 and $\infty$, because for the other values of p we merely obtain numerical approximations.

Example 1

We start with a simple pair of discrete mixing distributions

$$\begin{aligned} S(\{1\})=0.2, \quad S(\{2\})=0.3, \quad S(\{3\})=0.3, \quad S(\{4\})=0.2, \\ T(\{1\})=0.2, \quad T(\{2\})=0.4, \quad T(\{3\})=0.1, \quad T(\{4\})=0.3. \end{aligned}$$

The image of the parametric transformation $\{(S(\theta ),T(\theta )):\theta \in {\mathbb {R}}\}$ consists of 5 separate points

$$\begin{aligned} {\mathcal {U}}(S,T)= \{ (0,0),\; (0.2,0.2),\; (0.5,0.6),\; (0.8,0.7),\; (1,1)\}. \end{aligned}$$

We immediately notice that the greatest convex minorant and the smallest concave majorant of the points are piecewise linear functions

$$\begin{aligned} {\underline{H}}(u)= & {} \left\{ \begin{array}{ll} \frac{7}{8} u, &{}\quad 0< u \le 0.8, \\ \frac{3}{2} (u-1)+1, &{}\quad 0.8 \le u<1, \end{array} \right. \\ {\overline{H}}(u)= & {} \left\{ \begin{array}{ll} \frac{6}{5} u, &{}\quad 0< u \le 0.5, \\ \frac{4}{5} (u-1)+1, &{}\quad 0.5 \le u <1, \end{array} \right. \end{aligned}$$

with respective stepwise right-continuous derivatives

$$\begin{aligned} {\underline{h}}(u)= & {} \left\{ \begin{array}{ll} \frac{7}{8}, &{}\quad 0< u< 0.8, \\ \frac{3}{2} , &{}\quad 0.8 \le u<1, \end{array} \right. \\ {\overline{h}}(u)= & {} \left\{ \begin{array}{ll} \frac{6}{5}, &{}\quad 0< u< 0.5, \\ \frac{4}{5} , &{} \quad 0.5 \le u <1. \end{array} \right. \end{aligned}$$

Applying Corollary 1, we calculate

$$\begin{aligned} B_2(S,T)= & {} \sqrt{ \int _0^1 {\underline{h}}^2(u)\mathrm{d}u -1 } = \frac{1}{4}, \\ b_2(S,T)= & {} -\sqrt{ \int _0^1 {\overline{h}}^2(u)\mathrm{d}u -1 } = -\frac{1}{5}. \end{aligned}$$

Conclusions of Propositions 2 and 3 are following here

$$\begin{aligned} -\frac{1}{5}\le & {} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \le \frac{5}{16}, \\ -\frac{1}{5}\le & {} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\mathrm {ess\,sup\,}|X-{\mathbb {E}}X|} \le \frac{1}{8}. \end{aligned}$$

After changing the roles of S and T, we get

$$\begin{aligned} {\underline{h}}(u)= & {} \left\{ \begin{array}{ll} \frac{5}{6}, &{}\quad 0< u< 0.6, \\ \frac{5}{4} , &{}\quad 0.6 \le u<1, \end{array} \right. \\ {\overline{h}}(u)= & {} \left\{ \begin{array}{ll} \frac{8}{7}, &{}\quad 0< u< 0.7, \\ \frac{2}{3} , &{}\quad 0.7 \le u <1, \end{array} \right. \end{aligned}$$

and so

$$\begin{aligned} -\frac{5}{21}\le & {} \frac{{\mathbb {E}}X-{\mathbb {E}}Y}{{\mathbb {E}}|Y-{\mathbb {E}}Y|} \le \frac{5}{24}, \\ -\frac{1}{\sqrt{21}}\le & {} \frac{{\mathbb {E}}X-{\mathbb {E}}Y}{\sqrt{{\mathbb {V}}ar\,Y}} \le \frac{1}{2\sqrt{6}}, \\ -\frac{1}{7}\le & {} \frac{{\mathbb {E}}X-{\mathbb {E}}Y}{\mathrm {ess\,sup\,}|Y-{\mathbb {E}}Y|} \le \frac{1}{6}. \end{aligned}$$

The bounds shrink down towards 0 as p increases. This is evident due to the fact that by the Hölder inequality the scale units $\left( {\mathbb {E}}|X-{\mathbb {E}}X|^p\right) ^{1/p}$ increase in p. Besides, the classes of distributions G with finite pth moments decrease with increase of p. The only exception make here the lower bounds on ${\mathbb {E}}Y-{\mathbb {E}}X$ which are still equal to $- \frac{1}{5}$. This is caused by the fact that then the bounds are attained for two-point symmetric distributions G for which $\left( {\mathbb {E}}|X-{\mathbb {E}}X|^p\right) ^{1/p}$ are equal for all $1 \le p \le +\, \infty$.

Example 2

Suppose that the actual mixing distribution function is the power one $S(\theta )= 1-(1-\theta )^\alpha$, $0< \theta <1$, for some $\alpha >0$, whereas it is assumed that the mixing distribution function is another member of the power family $T(\theta )=1-(1-\theta )^\beta$ for $0< \beta \ne \alpha$. Set ${\mathcal {U}}(S,T)$ (see (2.2)) is the graph of increasing function

$$\begin{aligned} v(u)= T(S^{-1}(u)) = 1-(1-u)^{\beta /\alpha }, \quad 0\le u \le 1, \end{aligned}$$

transforming [0, 1] onto [0, 1]. It has the derivatives

$$\begin{aligned} v'(u)= & {} \frac{\beta }{\alpha }(1-u)^{\beta /\alpha -1}, \\ v''(u)= & {} - \frac{\beta }{\alpha }\left( \frac{\beta }{\alpha }-1\right) (1-u)^{\beta /\alpha -2}, \end{aligned}$$

which implies that v itself is convex if $\alpha >\beta$, and concave when $\alpha < \beta$. Accordingly, the greatest convex minorant and the smallest concave majorant of (2.2) have the forms ${\underline{H}}(u) = 1-(1-u)^{\beta /\alpha }$ and ${\overline{H}}(u)=u$, and their derivatives are ${\underline{h}}(u) = \frac{\beta }{\alpha }(1-u)^{\beta /\alpha -1}$ and ${\overline{h}}(u)=1$, when $\alpha > \beta$, and the functions change their roles if $\alpha < \beta$. By Theorem 1, every mixture distribution H of stochastically ordered family $\{F_\theta \}_{\theta \in {\mathbb {R}}}$ with respect to T satisfies the inequalities

$$\begin{aligned} G(x) \le H(x) \le 1-[1-G(x)]^{\beta /\alpha }, \end{aligned}$$

when $\alpha >\beta$ and the mixture of $\{F_\theta \}_{\theta \in {\mathbb {R}}}$ with respect to S is G, and the inequalities are reversed for $\alpha < \beta$.

Below we discuss the expectation bounds for the case $\alpha >\beta$ in greater detail, and merely mention the final results for $\alpha <\beta$ which are derived analogously. By Proposition 1, the upper bound on $\frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\left( {\mathbb {E}}|X-{\mathbb {E}}X|^p\right) ^{1/p}}$ is finite for given $1<p< \infty$ when $\int _0^1 (1-u)^{\left( \frac{\beta }{\alpha }-1 \right) \frac{p}{p-1}} \mathrm{d}u < \infty$, i.e., when the exponent is greater than $-\,1$, which is equivalent to $p > \frac{\alpha }{\beta }$. However, the bound does not have an analytic form except for the case $p=2$. The lower one is 0 for all $1<p < \infty$ (and for $p=1,\infty$ as well). When $\alpha <\beta$, the upper bound vanishes, and the lower one is negative finite for all $1 \le p \le \infty$.

If we have $\beta< \alpha <2\beta$, and fix $p=2$, we get

$$\begin{aligned} \int _0^1 {\underline{h}}^2(u) \mathrm{d}u = \left( \frac{\beta }{\alpha }\right) ^2 \int _0^1 (1-u)^{2\beta /\alpha -2}\mathrm{d}u = \frac{\beta ^2}{\alpha (2\beta -\alpha )}, \end{aligned}$$

and consequently

$$\begin{aligned} 0 \le \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\sqrt{{\mathbb {V}}ar\,X}} \le \frac{\alpha -\beta }{\sqrt{\alpha (2\beta -\alpha )}}. \end{aligned}$$

For $\alpha \ge 2\beta$, the right-hand side expression is replaced by $+\,\infty$. Similarly, we obtain

$$\begin{aligned} \frac{\alpha -\beta }{\sqrt{\alpha (2\beta -\alpha )}}\le \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\sqrt{{\mathbb {V}}ar\,X}} \le 0 \end{aligned}$$

for $\alpha <\beta$.

Proposition 2 asserts that

$$\begin{aligned} 0 \le \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \le + \,\infty \end{aligned}$$

for $\alpha >\beta$, but in the case $\alpha <\beta$ the respective lower bound is nontrivial, and we have

$$\begin{aligned} - \frac{\beta }{2\alpha } \le \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \le 0. \end{aligned}$$

For $p=\infty$, we have ${\underline{H}}\left( \frac{1}{2} \right) = 1 - 2^{-\beta /\alpha }$, and so

$$\begin{aligned} 0 \le \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\mathrm {ess\,sup\,}|X-{\mathbb {E}}X|} \le 2^{1-\beta /\alpha } -1 \end{aligned}$$

for $\alpha >\beta$. We easily check that the inequalities are reversed for $\alpha <\beta$. However, we do not claim that the zero bounds are optimal here. We finally observe that all the nonzero bounds tend to 0 as $\beta \rightarrow \alpha$.

Example 3

Suppose that one mixing distribution function is exponential with expectation 2, i.e., $S(\theta ) = 1-\exp (-\theta /2)$, $\theta >0$, and the alternative one is that of the sum of two independent standard exponentials, that is $T(\theta )=1-(1+\theta )\exp (-\theta )$, $\theta >0$. The composition

$$\begin{aligned} v(u)= T(S^{-1}(u))= 1-(1-u)^2 [1-2\ln (1-u)], \quad 0<u<1, \end{aligned}$$

represents set (2.2) for the above choice S and T. It is easily verified that v ranges over the whole standard unit interval, is strictly increasing, and convex on $(0, 1-e^{-1})$, and concave on $(1-e^{-1},1)$. The greatest convex minorant ${\underline{H}}$ of v is first coinciding with some convex part of v, and then linear. The breaking point is determined by the equation

$$\begin{aligned} 1-v(u)= (1-u)^2 [1-2\ln (1-u)] = (1-u)v'(u) = -4(1-u)^2 \ln (1-u), \end{aligned}$$

and amounts to $1-e^{-1/2} \approx 0.39347$ which satisfies $v'(1-e^{-1/2})= 2e^{-1/2}\approx 1.21306$. Therefore the greatest convex minorant and its derivative are following

$$\begin{aligned} {\underline{H}}(u) = \left\{ \begin{array}{ll} 1-(1-u)^2 [1-2\ln (1-u)], &{}\quad 0< u \le 1-e^{-1/2}, \\ 2e^{-1/2}(u-1)+1, &{}\quad 1-e^{-1/2} \le u <1, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} {\underline{h}}(u) = \left\{ \begin{array}{ll} -4(1-u)\ln (1-u), &{}\quad 0< u \le 1-e^{-1/2}, \\ 2e^{-1/2}, &{}\quad 1-e^{-1/2} \le u <1, \end{array} \right. \end{aligned}$$

respectively. The smallest concave majorant ${\overline{H}}$ of v is first linear, and then identical with v. The change point satisfies

$$\begin{aligned} v(u)= 1-(1-u)^2 [1-2\ln (1-u)] = uv'(u) = -4u(1-u) \ln (1-u). \end{aligned}$$

This does not have an analytic representation, and equals to $u_0\approx 0.87242$ so that $v'(u_0) \approx 1.05075$. The smallest concave majorant

$$\begin{aligned} {\overline{H}}(u) = \left\{ \begin{array}{ll} v'(u_0)u, &{}\quad 0< u \le u_0, \\ 1-(1-u)^2 [1-2\ln (1-u)], &{}\quad u_0 \le u <1, \end{array} \right. \end{aligned}$$

has the derivative

$$\begin{aligned} {\overline{h}}(u) = \left\{ \begin{array}{ll} v'(u_0), &{}\quad 0< u \le u_0, \\ -4(1-u)\ln (1-u), &{}\quad u_0 \le u <1. \end{array} \right. \end{aligned}$$

Note that both functions ${\underline{h}}$ and ${\overline{h}}$ are bounded here, and hence all the bounds of Propositions 1–3 are finite.

For establishing the standard deviation bounds with $p=2$, we use the following indefinite integral

$$\begin{aligned} v_2(u)= & {} \int _1^u [v'(t)]^2 \mathrm{d}t = 16 \int _1^u (1-t)^2 \ln ^2(1-t) \mathrm{d}t \\= & {} -16 (1-u)^3 \left[ \frac{1}{3} \ln ^2(1-u) - \frac{2}{9} \ln (1-u) + \frac{2}{27} \right] . \end{aligned}$$

The upper and lower bounds are

$$\begin{aligned} B_2(S,T)= & {} \sqrt{\int _0^1 {\underline{h}}^2(u)\mathrm{d}u-1} = \sqrt{v_2(1-e^{-1/2}) -v_2(0) + 4e^{-3/2}-1} \\= & {} \sqrt{\frac{5-8e^{-3/2}}{27}} \end{aligned}$$

and

$$\begin{aligned} b_2(S,T)=-\sqrt{\int _0^1 {\overline{h}}^2(u)\mathrm{d}u-1} = - \sqrt{u_0[v'(u_0)]^2 +v_2(1)-v_2(u_0)-1}, \end{aligned}$$

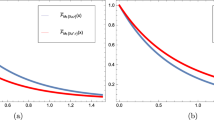
respectively. In the case $p=1$, we immediately check that $e^{-1/2}$ and $-\frac{1}{2} v'(u_0)$ are the upper and lower optimal evaluations. Since ${\underline{H}}\left( \frac{1}{2}\right) = 1-e^{-1/2}$ and ${\overline{H}}\left( \frac{1}{2}\right) = \frac{1}{2} v'(u_0)$, bounds (3.11) and (3.15) of Proposition 3 take on the forms $2 e^{-1/2}$ and $1-v'(u_0)$, respectively. Below we present numerical approximations of the above bounds

$$\begin{aligned} -\,0.52538\le & {} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{{\mathbb {E}}|X-{\mathbb {E}}X|} \le 0.60653,\\ -\,0.16684\le & {} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\sqrt{{\mathbb {V}}ar\,X}} \le 0.34507, \\ -\,0.05075\le & {} \frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\mathrm {ess\,sup\,}|X-{\mathbb {E}}X|} \le 0.21306. \end{aligned}$$

Example 4

We finally consider a pair of seemingly similar symmetric unimodal mixing distributions supported on [0, 1]. One is

$$\begin{aligned} S(\theta )= \left\{ \begin{array}{ll} \frac{3}{2} \theta ^2, &{}\quad 0< \theta< \frac{1}{2}, \\ 1-\frac{3}{2}(1-\theta )^2, &{}\quad \frac{1}{2} \le \theta <1, \end{array} \right. \end{aligned}$$

which has a symmetric triangular density, and an atom $\frac{1}{4}$ at the mode $\frac{1}{2}$. The other one

$$\begin{aligned} T(\theta )= \left\{ \begin{array}{ll} 4\theta ^3, &{}\quad 0< \theta< \frac{1}{2}, \\ 1-4(1-\theta )^3, &{}\quad \frac{1}{2} \le \theta <1, \end{array} \right. \end{aligned}$$

has quadratic density of different forms on $\left( 0, \frac{1}{2} \right)$ and $\left( \frac{1}{2} ,1 \right)$, and a sharp peak at $\frac{1}{2}$. Then

$$\begin{aligned} {\mathcal {U}}(S,T)= & {} \left\{ \left( u, \frac{8}{3} \sqrt{\frac{2}{3}} u^{3/2} \right) : \; 0 \le u< \frac{3}{8} \right\} \\&\cup \left\{ \left( u, 1- \frac{8}{3} \sqrt{\frac{2}{3}} (1-u)^{3/2} \right) : \; \frac{5}{8} \le u < 1 \right\} . \end{aligned}$$

The first pairs represent the graph of convex increasing function, and that of the latter is concave increasing. The greatest convex minorant of ${\mathcal {U}}(S,T)$ has three different parts: function $v(u) = \frac{8}{3} \sqrt{\frac{2}{3}} u^{3/2}$ on some right neighborhood of 0, then a straight line joining the graph of v with point $\left( \frac{5}{8}, \frac{1}{2}\right)$, and ultimately another piece of line passing between $\left( \frac{5}{8}, \frac{1}{2}\right)$ and $\left( 1,1\right)$. The point of change from strictly convex v into the first linear one is determined by the slope equality condition

$$\begin{aligned} v'(u)= \frac{\frac{1}{2}-v(u)}{\frac{5}{8} -u} \end{aligned}$$

for some $0< u < \frac{3}{8}$ which can be rewritten as

$$\begin{aligned} 8 \sqrt{2} \left( \sqrt{u}\right) ^{3}- 15\sqrt{2} \sqrt{u}+3 \sqrt{3}=0. \end{aligned}$$

The cubic function of real argument replacing $\sqrt{u}$ has three real roots $- \frac{\sqrt{3}}{2}- \frac{\sqrt{6}}{4}< \frac{\sqrt{3}}{2}- \frac{\sqrt{6}}{4} < \frac{\sqrt{6}}{2}$, and only the middle one is located in (0, 1). Therefore our change point is $\left( \frac{\sqrt{3}}{2}- \frac{\sqrt{6}}{4} \right) ^2= \frac{9}{8} - \frac{3}{4} \sqrt{2} \approx 0.064340$ so that $v'\left( \frac{9}{8} - \frac{3}{4} \sqrt{2}\right) = 2 \sqrt{2} -2 \approx 0.82843$. Accordingly,

$$\begin{aligned} {\underline{H}}(u) = \left\{ \begin{array}{ll} \frac{8}{3} \sqrt{\frac{2}{3}} u^{3/2}, &{}\quad 0 \le u \le \frac{9}{8} - \frac{3}{4} \sqrt{2}, \\ (2 \sqrt{2} -2) \left( u- \frac{5}{8} \right) + \frac{1}{2}, &{}\quad \frac{9}{8} - \frac{3}{4} \sqrt{2} \le u \le \frac{5}{8}, \\ \frac{4}{3} (u-1) +1, &{}\quad \frac{5}{8} \le u \le 1, \end{array} \right. \end{aligned}$$

and its derivative is

$$\begin{aligned} {\underline{h}}(u) = \left\{ \begin{array}{ll} 4\sqrt{\frac{2u}{3}} , &{}\quad 0 \le u \le \frac{9}{8} - \frac{3}{4} \sqrt{2}, \\ 2 \sqrt{2} -2 , &{}\quad \frac{9}{8} - \frac{3}{4} \sqrt{2} \le u< \frac{5}{8}, \\ \frac{4}{3} , &{}\quad \frac{5}{8} \le x < 1. \end{array} \right. \end{aligned}$$

Therefore

$$\begin{aligned} B_2^2 (S,T)= & {} \int _0^{\frac{9}{8} - \frac{3}{4} \sqrt{2}}\, \frac{32u}{3} \,\mathrm{d}u+ (2 \sqrt{2} -2)^2 \left( \frac{3}{4} \sqrt{2} - \frac{1}{2} \right) \\&+ \left( \frac{4}{3} \right) ^2 \frac{3}{8} -1 = 4 \sqrt{2} - 5 \frac{7}{12}, \end{aligned}$$

and $B_2 (S,T) = \sqrt{4 \sqrt{2}- 5 \frac{7}{12} }\approx 0.27115$ is the sharp upper bound on $\frac{{\mathbb {E}}Y-{\mathbb {E}}X}{\sqrt{{\mathbb {V}}ar\,X}}$. Furthermore, $B_1(S,T)= \frac{1}{2} [ {\underline{h}}(1)-{\underline{h}}(0)] = \frac{2}{3}$ and $B_\infty (S,T)= 1- 2{\underline{H}}\left( \frac{1}{2} \right) =\frac{\sqrt{2}-1}{2} \approx 0.20711$ provide analogous bounds expressed in ${\mathbb {E}} |X-{\mathbb {E}}X|$ and $\mathrm {ess\,sup\,}|X-{\mathbb {E}}X|$ units, respectively.

Since ${\overline{H}}(u) = 1-{\underline{H}}(1-u)$, and ${\overline{h}}(u)= {\underline{h}}(1-u)$, we easily deduce that $b_p(S,T)=-B_p(S,T)$, $1 \le p \le +\,\infty$, which means that the sharp lower bounds are the negatives of their upper counterparts.

5 Proof of Theorem 1

We prove the first inequality in (2.1) for every fixed value $u=G(x) \in [0,1]$. It is evident that for $u= G(x) = \int _{\mathbb {R}} F_\theta (x) S(\mathrm{d}\theta )=0$, we can take $F_\theta (x)=0$, $\theta \in {\mathbb {R}}$, which guarantees the smallest possible value of $\int _{\mathbb {R}} F_\theta (x) T(\mathrm{d}\theta )=0$.

For fixed $0< u \le 1$, we solve an auxiliary minimization problem for discrete approximations of $F_\theta (x)$, $\theta \in {\mathbb {R}}$. Consider a finite partition of real axis ${\mathbb {R}}= \bigcup _{i=1}^n \Theta _i$, where $\Theta _1 \prec \cdots \prec \Theta _n$ are disjoint ordered intervals. Each interval either has or does not have the left and right end-point. Define $s_i=S(\Theta _i)$, $t_i=T(\Theta _i)$, and denote by $u_i$ unknown constant values of $F_\theta (x)$ on $\Theta _i$, $i=1,\ldots ,n$. The only restrictions on them are $1 \ge u_1 \ge \cdots \ge u_n \ge 0$, and $\int _{\mathbb {R}} F_\theta (x) S(d\theta )= \sum _{i=1}^n s_iu_i =u$. Our auxiliary problem is to minimize $\int _{\mathbb {R}} F_\theta (x) T(\mathrm{d}\theta )= \sum _{i=1}^n t_iu_i$ under the constraints on $u_1, \ldots , u_n$. By the change of variables

$$\begin{aligned} v_n= & {} u_n \ge 0, \\ v_i= & {} u_i-u_{i+1} \ge 0, \quad i=1, \ldots ,n-1, \end{aligned}$$

satisfying also $\sum _{i=1}^nv_i=u_1\le 1$, we have

$$\begin{aligned} \sum _{i=1}^n u_is_i= & {} \sum _{i=1}^n \left( \sum _{j=i}^n v_j\right) s_i = \sum _{i=1}^n \left( \sum _{j=1}^i s_j\right) v_i = \sum _{i=1}^n S_i v_i, \\ \sum _{i=1}^n u_it_i= & {} \sum _{i=1}^n T_i v_i, \end{aligned}$$

where $S_i= \sum _{j=1}^i s_j$, $T_i= \sum _{j=1}^i t_j$, $i=1,\ldots ,n$, are known and satisfy $0 \le S_1 \le \cdots \le S_n=1$ and $0 \le T_1 \le \cdots \le T_n=1$.

Our problem can be rewritten as to minimize $\sum _{i=1}^nT_iv_i$ over the intersection of the simplex

$$\begin{aligned} {\mathcal {S}}_n= \left\{ (v_1,\ldots ,v_n): \; v_i\ge 0, \; i=1,\ldots ,n, \; \sum _{i=1}^n v_i\le 1 \right\} \end{aligned}$$

and hyperplane

$$\begin{aligned} {\mathcal {H}}_S= \left\{ (v_1,\ldots ,v_n): \; \sum _{i=1}^n S_i v_i =u \right\} . \end{aligned}$$

The simplex is a convex polyhedron with vertices ${\mathbf {0}}$, being the zero vector, and ${\mathbf {e}}_i$, $i=1,\ldots ,n$, which are the standard unit vectors in ${\mathbb {R}}^n$. Clearly, the line segments joining the extreme points constitute the edges of ${\mathcal {S}}_n$. The intersection ${\mathcal {S}}_n \cap {\mathcal {H}}_S$ is a convex set as well, and all its extreme points belong to some edges of ${\mathcal {S}}^n$. All the edges can be represented as

$$\begin{aligned}&\alpha \,{\mathbf {e}}_i + (1-\alpha )\, {\mathbf {0}},\quad 1 \le i \le n, \\&\alpha \,{\mathbf {e}}_i + (1-\alpha )\, {\mathbf {e}}_j, \quad 1 \le i < j \le n, \end{aligned}$$

for all $0 \le \alpha \le 1$. In the first case, $\alpha \,{\mathbf {e}}_i \in {\mathcal {H}}_S$ iff $S_i \ge u$ and

$$\begin{aligned} v_k= \left\{ \begin{array}{ll} \frac{u}{S_i}, &{}\quad k=i, \\ 0, &{}\quad \mathrm {otherwise}. \end{array} \right. \end{aligned}$$

(5.1)

In the latter one, $\alpha \,{\mathbf {e}}_i + (1-\alpha )\, {\mathbf {e}}_j \in {\mathcal {H}}_S$ iff $S_i \le u \le S_j$ and $\alpha S_i + (1-\alpha )S_j =u$. If either $u=S_i$ or $u=S_j$, then either ${\mathbf {e}}_i \in {\mathcal {H}}_S$ or ${\mathbf {e}}_j \in {\mathcal {H}}_S$, respectively. These come under the provisions of the previous case. When $S_i< u < S_j$, the respective vector has the coordinates

$$\begin{aligned} v_k= \left\{ \begin{array}{ll} \frac{S_j-u}{S_j-S_i} , &{}\quad k=i, \\ \frac{u-S_i}{S_j-S_i} , &{}\quad k=j, \\ 0, &{}\quad \mathrm {otherwise.} \end{array} \right. \end{aligned}$$

(5.2)

The linear functional $\sum _{i=1}^n T_i v_i$ attains its minimal value on the convex compact set ${\mathcal {S}}_n \cap {\mathcal {H}}_S$ at some its extreme points. This means that it suffices to confine analysis to the finite set of points (5.1) if $u \le S_i$, and (5.2) if $S_i< u < S_j$. Coming back to the original variables we conclude that the possible candidates for the minimum points are $(u_1, \ldots , u_n)$ with

$$\begin{aligned} u_k = \left\{ \begin{array}{ll} \frac{u}{S_i}, &{}\quad k=1, \ldots ,i, \\ 0, &{}\quad k=i+1, \ldots , n, \end{array} \right. \quad \mathrm {if}\; u \le S_i, \end{aligned}$$

(5.3)

and

$$\begin{aligned} u_k = \left\{ \begin{array}{ll} 1, &{}\quad k=1,\ldots ,i, \\ \frac{ u-S_i}{S_j-S_i}, &{}\quad k=i+1, \ldots ,j, \\ 0, &{}\quad k=j+1, \ldots , n, \end{array} \right. \quad \mathrm {if}\; S_i< u < S_j. \end{aligned}$$

(5.4)

Adding $i=0$ with $S_0=0$, we can jointly represent (5.3) and (5.4) by the formula

$$\begin{aligned} u_k = \left\{ \begin{array}{ll} 1, &{}\quad k=1,\ldots ,i, \\ \frac{ u-S_i}{S_j-S_i}, &{}\quad k=i+1, \ldots ,j, \\ 0, &{}\quad k=j+1, \ldots , n, \end{array} \right. \quad \mathrm {if}\;S_i< u \le S_j, \;0 \le i < j \le n. \end{aligned}$$

(5.5)

Note that for $i=0$ and $j=n$, the first and last options in (5.5) are empty, respectively.

Accordingly, for given $u=G(x)$ and $F_\theta (x)$, $\theta \in {\mathbb {R}}$, constant on the intervals of finite partition $\Theta _1 \prec \cdots \prec \Theta _n$ there exist $0 \le i < j \le n$ such that $S_i=S\left( \bigcup _{k=1}^i \Theta _k \right) < u \le S_j=S\left( \bigcup _{k=1}^j \Theta _k \right)$ which provide the minimal value of

$$\begin{aligned} \sum _{k=1}^n t_k u_k= & {} \sum _{k=1}^i t_k + \frac{ u-S_i}{S_j-S_i} \sum _{k=i+1}^j t_k \\= & {} T\left( \bigcup _{k=1}^i \Theta _k \right) + \frac{T\left( \bigcup _{k=i+1}^j \Theta _k \right) }{ S\left( \bigcup _{k=i+1}^j \Theta _k \right) } \left[ u- S\left( \bigcup _{k=1}^i \Theta _k \right) \right] . \end{aligned}$$

This means that in this case it suffices to partition the parameter set ${\mathbb {R}}$ onto at most three intervals $\Theta _1 \prec \Theta _2 \prec \Theta _3$ such that $S(\Theta _1) < u \le S(\Theta _1 \cup \Theta _2)$. Observe that $\Theta _1$ and/or $\Theta _3$ may be empty so that $S(\Theta _1)=0$ and/or $S( \Theta _1 \cup \Theta _2)=1$. For given S, T, and $0< u \le 1$, we define

$$\begin{aligned} {\underline{H}}(u) = \inf \left\{ T\left( \Theta _1 \right) + \frac{T\left( \Theta _2 \right) }{ S\left( \Theta _2 \right) } \left[ u- S\left( \Theta _1 \right) \right] \right\} , \end{aligned}$$

(5.6)

where the infimum is taken over all partitions $\Theta _1 \prec \Theta _2 \prec \Theta _3$ of the real line satisfying $S(\Theta _1) < u \le S(\Theta _1 \cup \Theta _2)$. Observe that

$$\begin{aligned} S(\Theta _1) = \left\{ \begin{array}{lll} 0, &{}\quad \mathrm {if} &{} \Theta _1 = \emptyset , \\ S(\theta _1-), &{}\quad \mathrm {if} &{} \Theta _1 =(-\,\infty , \theta _1), \\ S(\theta _1), &{}\quad \mathrm {if} &{} \Theta _1 =(-\,\infty , \theta _1], \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} S(\Theta _2) = \left\{ \begin{array}{lll} S(\theta _2-)- S(\Theta _1), &{}\quad \mathrm {if} &{} \Theta _1 \cup \Theta _2=(-\,\infty , \theta _2), \\ S(\theta _2)- S(\Theta _1), &{}\quad \mathrm {if} &{} \Theta _1 \cup \Theta _2=(-\,\infty , \theta _2], \end{array} \right. \end{aligned}$$

for some $\theta _1 < \theta _2$, and similar relations hold for $T(\Theta _1)$ and $T(\Theta _2)$. This means that for given $0<u\le 1$, ${\underline{H}}(u)$ is the infimum over the values of all linear functions joining points $(S(\theta _1\mp ),T(\theta _1\mp ))$ and $(S(\theta _2\mp ),T(\theta _2\mp ))$ for which $S(\theta _1\mp )< u \le S(\theta _2\mp )$ at argument u. This defines the greatest convex minorant of the set of points $\{ (S(\theta -),T(\theta -)),\; (S(\theta ),T(\theta )): \; \theta \in {\mathbb {R}} \}$ on interval [0, 1] when we let vary u over the interval. Obviously, the greatest convex minorant does not change if we drop the left-limit values.

A trivial but important observation is that the same partition $\Theta _1 \prec \Theta _2 \prec \Theta _3$ may provide the infimum in (5.6) for various u. In particular, if the infimum is attained when $S( \Theta _2)=1$, then ${\underline{H}}(u)= {\underline{u}}\,u$ with ${\underline{u}}$ defined in (2.6) for every $u \in [0,1]$. Another extremity is that ${\underline{H}}(u)$ is approached as $S(\Theta _2) \searrow 0$, and the linear functions in (5.6) tend to the tangent of ${\mathcal {U}}(S,T)$ at u. In this case, one needs to perform separate approximations for single values of u.

We prove that (5.6) satisfies the left hand-side inequality in (2.1). Let $F_\theta (x)$ for fixed x be a non-increasing function of $\theta \in {\mathbb {R}}$ taking values in [0, 1] and satisfying $\int _{\mathbb {R}}F_\theta (x) S(\mathrm{d}\theta ) = u$. If $F_\theta (x)$, $\theta \in {\mathbb {R}}$, take on finitely many values $(u_1, \ldots , u_n)$, we proved above that there exists ${\underline{F}}_\theta (x)$, $\theta \in {\mathbb {R}}$, with no more than three values 0, $0< c < 1$ and 1, satisfying the assumptions and such that

$$\begin{aligned} \int _{\mathbb {R}}{\underline{F}}_\theta (x) T(\mathrm{d}\theta ) \le \int _{\mathbb {R}}F_\theta (x) T(\mathrm{d}\theta ), \end{aligned}$$

and the infimum over these at most three-valued functions is just ${\underline{H}}(u)$.

If $F_\theta (x)$, $\theta \in {\mathbb {R}}$, has an infinite image set, we need more subtle arguments. Since it is monotone, nonnegative and bounded above, we can write

$$\begin{aligned} u= \int _{\mathbb {R}}F_\theta (x) S(\mathrm{d}\theta )= & {} \inf _{A_1,\ldots , A_{m}} \sum _{i=1}^{m} \sup _{\theta \in A_i} F_\theta (x) S(A_i), \\ \int _{\mathbb {R}}F_\theta (x) T(\mathrm{d}\theta )= & {} \inf _{B_1,\ldots , B_{m}} \sum _{i=1}^{m} \sup _{\theta \in B_i} F_\theta (x) T(B_i), \end{aligned}$$

where $\{A_1,\ldots , A_{m}\}$ and $\{B_1,\ldots , B_{m}\}$ are arbitrary finite partitions of ${\mathbb {R}}$ onto disjoint intervals. This means that there exist increasing sequences of partitions $\{A^m_1,\ldots , A^m_{i_m}\}$, $\{B^m_1,\ldots , B^m_{j_m}\}$, $m=1,2,\ldots$, such that

$$\begin{aligned} u_m= & {} \sum _{i=1}^{i_m} \sup _{\theta \in A^m_i} F_\theta (x) S(A^m_i)\quad \searrow \quad u= \int _{\mathbb {R}}F_\theta (x) S(\mathrm{d}\theta ) , \\&\sum _{j=1}^{j_m} \sup _{\theta \in B^m_j} F_\theta (x) T(B^m_j) \quad \searrow \quad \int _{\mathbb {R}}F_\theta (x) T(\mathrm{d}\theta ) , \end{aligned}$$

as $m \rightarrow \infty$. Let $\{ C^m_1,\ldots , C^m_{k_m}\}$ be the partition of ${\mathbb {R}}$ composed of intersections $A^m_i \cap B^m_j$, $i=1, \ldots , i_m$, $j=1, \ldots , j_m$. Then

$$\begin{aligned} \sum _{i=1}^{i_m} \sup _{\theta \in A^m_i} F_\theta (x) S(A^m_i)\ge & {} \sum _{k=1}^{k_m} \sup _{\theta \in C^m_k} F_\theta (x) S(C^m_k) = v_m \\&\searrow \quad u=\int _{\mathbb {R}}F_\theta (x) S(\mathrm{d}\theta ) >0 , \\ \sum _{j=1}^{j_m} \sup _{\theta \in B^m_j} F_\theta (x) T(B^m_j)\ge & {} \sum _{k=1}^{k_m} \sup _{\theta \in C^m_k} F_\theta (x) T(C^m_k) \searrow \int _{\mathbb {R}}F_\theta (x) T(\mathrm{d}\theta ). \end{aligned}$$

Functions

$$\begin{aligned} F^m_\theta (x) = \frac{u}{v_m} \sum _{k=1}^{k_m} \sup _{\theta \in C^m_k} F_\theta (x) {\mathbf {1}}_{C^m_k}(\theta ), \quad \theta \in {\mathbb {R}}, \end{aligned}$$

are non-increasing, have finite numbers of values in [0, 1], and integrate to u with respect to measure S. Therefore

$$\begin{aligned} {\underline{H}}(u)\le & {} \int _{\mathbb {R}}F^m_\theta (x) T(\mathrm{d}\theta ) = \frac{u}{v_m} \sum _{k=1}^{k_m} \sup _{\theta \in C^m_k} F_\theta (x) T(C^m_k) \\\rightarrow & {} \int _{\mathbb {R}}F^m_\theta (x) T(\mathrm{d}\theta ) \ge {\underline{H}}(u), \end{aligned}$$

which is our claim.

We proved that for every fixed $x \in {\mathbb {R}}$, there exists function ${\underline{F}}_\theta (x)$, $\theta \in {\mathbb {R}}$, with at most three values in [0, 1] which satisfies (1.2) and provides the minimal value of (1.3) which amounts to (2.3). Letting x vary over ${\mathbb {R}}$, we obtain two-variable function ${\underline{F}}: {\mathbb {R}}^2 \mapsto [0,1]$ which can be treated as a family of functions $\{ {\underline{F}}_\theta \}_{\theta \in {\mathbb {R}}}$ in variable x. Our aim is to prove that the construction defines a family of stochastically ordered distribution functions.

To this end, we first perform some auxiliary considerations. Define

$$\begin{aligned} {\overline{A}}= \{ 0 \le u \le 1: \exists \,\,\theta \in {\mathbb {R}}\; (u, {\underline{H}}(u)) = (S(\theta \pm ), T(\theta \pm ))\}. \end{aligned}$$

This notation means that either $(u, {\underline{H}}(u))= (S(\theta ), T(\theta ))$ or $(u, {\underline{H}}(u))= (S(\theta -),$$T(\theta -))$. This is a closed subset of [0, 1] which can be represented as an at most countable sum of disjoint closed, possibly degenerate intervals ${\overline{A}}= \bigcup _j {\overline{A}}_j$. Then its interior is a sum of disjoint open intervals $A= \mathrm {int}\,{\overline{A}} = \bigcup _j A_j$. Note that the number of open intervals can be less than the number of the closed ones. The border of A consists of at most countably many separate points

$$\begin{aligned} C = \partial {\overline{A}} = {\overline{A}} {\setminus } A = \bigcup _j \{ c_j\}. \end{aligned}$$

We finally introduce

$$\begin{aligned} B = [0,1] {\setminus } {\overline{A}}= \{ 0 \le u \le 1: \; \forall \,\,\theta \in {\mathbb {R}}\; (u, {\underline{H}}(u)) \ne (S(\theta \pm ), T(\theta \pm ))\} \end{aligned}$$

which means that neither $(u, {\underline{H}}(u))= (S(\theta ), T(\theta ))$ nor $(u, {\underline{H}}(u))= (S(\theta -),$$T(\theta -))$. Obviously, this is a sum of no more than countably many disjoint intervals $B = \bigcup _j B_j$. The closures of B and $B_j$ are denoted by ${\overline{B}}$, and ${\overline{B}}_j$, respectively. Summing up, each pair (S, T) generates a partition of the unit interval

$$\begin{aligned}{}[0,1]= \bigcup _j A_j \cup \bigcup _j B_j \cup \bigcup _j \{ c_j \} . \end{aligned}$$

(5.7)

It is obvious that for every $A_j,A_k \subset A$, $A_j \prec A_k$, there exists $B_l \subset B$ such that $A_j \prec B_l \prec A_k$. This is not necessarily true if we replace the roles of subintervals of A and B. However, for every pair of subintervals from A and B there exists point $c_l$ separating them.

For every $G(x) = u \in A$ there exists $\theta = \theta _u \in {\mathbb {R}}$ such that $(u, {\underline{H}}(u))= (S(\theta ), T(\theta ))$. This is not uniquely determined, though. We denote the set of all $\theta$ satisfying the condition by $\Theta ^u$. We also define $\Theta ^{A_j} = \bigcup _{u \in A_j} \Theta ^u$. Similarly, for every $c_j \in C$ there exists real $\theta _{c_j}$ satisfying either $(c_j, {\underline{H}}(c_j))= (S(\theta _{c_j}), T(\theta _{c_j}))$ or $(c_j, {\underline{H}}(c_j))= (S(\theta _{c_j} -),$$T(\theta _{c_j} -))$. This is unique in the latter case, but otherwise may be many $\theta$’s satisfying the condition. We denote the set of all $\theta$ sharing the property by $\Theta ^{c_j}$. Finally, for $B_j = {\overline{B}}_j {\setminus } \{ c_k, c_l \}$ with $c_k < c_l$, define

$$\begin{aligned} \Theta ^{B_j} = \{ \theta \in {\mathbb {R}}: \; \forall \,\, \theta _1 \in \Theta ^{c_k}, \; \theta _2 \in \Theta ^{c_l}\;\; \theta _1< \theta < \theta _2 \}. \end{aligned}$$

Then we have a partition of the parameter set

$$\begin{aligned} {\mathbb {R}}= \bigcup _j \Theta ^{A_j} \cup \bigcup _j \Theta ^{B_j} \cup \bigcup _j \Theta ^{c_j} . \end{aligned}$$

For any two elements $D_k \prec D_l$ of the partition (5.7) we have $\Theta ^{D_k} \prec \Theta ^{D_l}$. Moreover, inequality $u<v$ for some $u,v \in A_j$ implies $\Theta ^u \prec \Theta ^v$ as well.

From the solution of the local minimization problems for various $u= G(x)$, we conclude the following minimization conditions. If $u \in A_j = (c_k,c_l)$, say, then

$$\begin{aligned} {\underline{F}}_\theta (x) = \left\{ \begin{array}{lll} 1, &{}\quad \mathrm {if} &{} \theta \preceq \Theta ^u, \\ 0, &{}\quad \mathrm {if} &{} \theta \succ \Theta ^u. \end{array} \right. \end{aligned}$$

(5.8)

The above notation, introduced for brevity, means that $\theta \prec (\succ )\, \Theta ^u$ when $\{\theta \} \prec (\succ )\, \Theta ^u$, and $\theta \preceq (\succeq )\, \Theta ^u$ when either $\{\theta \} \prec (\succ )\, \Theta ^u$ or $\theta \in \Theta ^u$. For $u \in {\overline{B}}_j=[c_k,c_l]$, say, we have four possible cases. We take

$$\begin{aligned} {\underline{F}}_\theta (x) = \left\{ \begin{array}{lll} 1, &{}\quad \mathrm {if} &{} \theta \preceq \Theta ^{c_k}, \\ \frac{G(x)-S(\theta _{c_k})}{S(\theta _{c_l})-S(\theta _{c_k})}, &{}\quad \mathrm {if} &{} \Theta ^{c_k}\prec \theta \preceq \Theta ^{c_l}, \\ 0, &{}\quad \mathrm {if} &{} \theta \succ \Theta ^{c_l}, \end{array} \right. \end{aligned}$$

(5.9)

if $(c_k, {\underline{H}}(c_k))= (S(\theta _{c_k}), T(\theta _{c_k}))$ and $(c_l, {\underline{H}}(c_l))= (S(\theta _{c_l}), T(\theta _{c_l}))$ for $\theta _{c_k}$ and $\theta _{c_l}$, being some representatives of $\Theta ^{c_k}$ and $\Theta ^{c_l}$, respectively. Moreover,

$$\begin{aligned} {\underline{F}}_\theta (x) = \left\{ \begin{array}{lll} 1, &{}\quad \mathrm {if} &{} \theta \prec \Theta ^{c_k}, \\ \frac{G(x)-S(\theta _{c_k}-)}{S(\theta _{c_l-})-S(\theta _{c_k}-)}, &{}\quad \mathrm {if} &{} \Theta ^{c_k}\preceq \theta \prec \Theta ^{c_l}, \\ 0, &{}\quad \mathrm {if} &{} \theta \succeq \Theta ^{c_l}, \end{array} \right. \end{aligned}$$

(5.10)

when $(c_k, {\underline{H}}(c_k))= (S(\theta _{c_k}-), T(\theta _{c_k}-))$ and $(c_l, {\underline{H}}(c_l))= (S(\theta _{c_l}-), T(\theta _{c_l}-))$, and

$$\begin{aligned} {\underline{F}}_\theta (x) = \left\{ \begin{array}{lll} 1, &{}\quad \mathrm {if} &{} \theta \preceq \Theta ^{c_k}, \\ \frac{G(x)-S(\theta _{c_k})}{S(\theta _{c_l-})-S(\theta _{c_k})}, &{}\quad \mathrm {if} &{} \Theta ^{c_k}\prec \theta \prec \Theta ^{c_l}, \\ 0, &{}\quad \mathrm {if} &{} \theta \succeq \Theta ^{c_l}, \end{array} \right. \end{aligned}$$

(5.11)

if $(c_k, {\underline{H}}(c_k))= (S(\theta _{c_k}), T(\theta _{c_k}))$ and $(c_l, {\underline{H}}(c_l))= (S(\theta _{c_l}-), T(\theta _{c_l}-))$, and finally

$$\begin{aligned} {\underline{F}}_\theta (x) = \left\{ \begin{array}{lll} 1, &{}\quad \mathrm {if} &{} \theta \prec \Theta ^{c_k}, \\ \frac{G(x)-S(\theta _{c_k}-)}{S(\theta _{c_l})-S(\theta _{c_k}-)}, &{}\quad \mathrm {if} &{} \Theta ^{c_k}\preceq \theta \preceq \Theta ^{c_l}, \\ 0, &{}\quad \mathrm {if} &{} \theta \succ \Theta ^{c_l}, \end{array} \right. \end{aligned}$$

(5.12)

if $(c_k, {\underline{H}}(c_k))= (S(\theta _{c_k}-), T(\theta _{c_k}-))$ and $(c_l, {\underline{H}}(c_l))= (S(\theta _{c_l}), T(\theta _{c_l}))$. We easily check that in all the cases (5.8)–(5.12) imply

$$\begin{aligned} \int _{\mathbb {R}}{\underline{F}}_\theta (x) S(\mathrm{d}\theta )= & {} G(x), \\ \int _{\mathbb {R}}{\underline{F}}_\theta (x) T(\mathrm{d}\theta )= & {} {\underline{H}}(G(x)). \end{aligned}$$

where ${\underline{H}}(G(x))= T(\theta _u)$ for (5.8), and ${\underline{H}}(G(x))= T(\theta _{c_k}\pm ) + \frac{T(\theta _{c_l}\pm )-T(\theta _{c_k}\pm )}{S(\theta _{c_l}\pm )-(\theta _{c_k}\pm )} [u- S(\theta _{c_k}\pm )]$ with properly chosen limits at $c_k$ and $c_l$ in the other cases.

Now we rewrite the above formulae fixing $\theta \in {\mathbb {R}}$, and letting x vary. Assume first

(A1) :

$\theta \in \Theta ^u \subset \Theta ^{A_j}$ for some $u=G(x) \in A_j \subset A$.

Then ${\underline{F}}_\theta (x)=1$ by (5.8). Take $u>v =G(y) \in A$ (we admit $v \in A_j$ as well as $v \in A_k \prec A_j$). Since

$$\begin{aligned} {\underline{F}}_\theta (y) = \left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\; \theta \succ \Theta ^v, \\ 1, &{}\quad \mathrm {otherwise}, \end{array} \right. \end{aligned}$$

and $\Theta ^u \succ \Theta ^v$, we obtain ${\underline{F}}_\theta (y)=0$. Assume now that $v=G(y) \in {\overline{B}}_j=[c_k,c_l]$ for some ${\overline{B}}_j \prec A_j$. Then $\Theta ^u \succ \Theta ^{c_l}$ and any of (5.9)–(5.12) implies that ${\underline{F}}_\theta (y) =0$ for all $\theta \in \Theta ^u$. Similar arguments show that ${\underline{F}}_\theta (y) =1$ if $G(y)>G(x)$ and either $G(y) \in A$ or $G(y) \in {\overline{B}}$. This shows that for every $\theta \in \Theta ^{G(x)}$ such that $G(x) \in A$, we have

$$\begin{aligned} {\underline{F}}_\theta (y) = \left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\; G(y) < G(x), \\ 1, &{}\quad \mathrm {if}\; G(y) \ge G(x), \end{array} \right. \end{aligned}$$

(5.13)

Consider now the set of parameters $\theta$ such that

(A2) :

$\Theta ^{c_k} \prec \theta \preceq \Theta ^{c_l}$ for some $(c_k,c_l) = B_j$, with $(c_k,{\underline{H}}(c_k)) = (S(\theta _{c_k}),T(\theta _{c_k}))$, and $(c_l,{\underline{H}}(c_l))$$= (S(\theta _{c_l}),T(\theta _{c_l}))$.

Then for every x such that $G(x) = u \in [c_k,c_l]$ we have

$$\begin{aligned} {\underline{F}}_\theta (x) = \frac{G(x)-S(\theta _{c_k})}{S(\theta _{c_l})-S(\theta _{c_k})}. \end{aligned}$$

(cf (5.9)). If $G(x) =v \in A_k \prec {\overline{B}}_j$, then $\Theta ^v \prec \Theta ^{c_k} \prec \theta$, and ${\underline{F}}_\theta (x)=0$ by (5.8). Certainly, ${\underline{F}}_\theta (x)=1$ if $G(x) =v \in A_k \succ {\overline{B}}_j$, because $\Theta ^v \succ \Theta ^{c_l}$.

If $G(x) \in {\overline{B}}_i =[c_p,c_q] \prec {\overline{B}}_j$, we obtain $\Theta ^{c_q} \prec \Theta ^{c_k} \prec \theta$, and each of (5.9)–(5.12) implies ${\underline{F}}_\theta (x) =0$. If $G(x) \in {\overline{B}}_i\setminus \{c_k\} = [c_p, c_k)$, relation $\Theta ^{c_k} \prec \theta$ provides the same conclusion by (5.9) and (5.12). When $G(x) \in {\overline{B}}_i = [c_p, c_q]$ with $c_p \ge c_l$, we have two possibilities. When $c_p > c_l$, we apply the relation $\Theta ^{c_l} \prec \Theta ^{c_p}$, possibly together with $\theta \prec \Theta ^{c_l}$, to obtain ${\underline{F}}_\theta (x) =1$. Suppose now that $G(x) \in (c_l,c_q]$. Applying formulae (5.9) and (5.11), we conclude again ${\underline{F}}_\theta (x) =1$ from condition $\theta \preceq \Theta ^{c_l}$. Accordingly, for $\theta$’s satisfying assumption (A2) we have

$$\begin{aligned} {\underline{F}}_\theta (x) = \left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\; G(x) \le S(\theta _{c_k}), \\ \frac{G(x)-S(\theta _{c_k})}{S(\theta _{c_l})-S(\theta _{c_k})}, &{}\quad \mathrm {if}\; S(\theta _{c_k})\le G(x) \le S(\theta _{c_l}), \\ 1, &{}\quad \mathrm {if}\; G(x) \ge S(\theta _{c_l}), \end{array} \right. \end{aligned}$$

(5.14)

which is a proper distribution function on ${\mathbb {R}}$.

Using much the same arguments, we deduce that for parameters $\theta$ satisfying the conditions

(A3) :

$\Theta ^{c_k} \preceq \theta \prec \Theta ^{c_l}$ for some $(c_k,c_l) = B_j$, with $(c_k,{\underline{H}}(c_k)) = (S(\theta _{c_k}-),T(\theta _{c_k}-))$, and $(c_l,{\underline{H}}(c_l)) = (S(\theta _{c_l}-),T(\theta _{c_l}-))$,

(A4) :

$\Theta ^{c_k} \prec \theta \prec \Theta ^{c_l}$ for some $(c_k,c_l) = B_j$, with $(c_k,{\underline{H}}(c_k)) = (S(\theta _{c_k}),T(\theta _{c_k}))$, and $(c_l,{\underline{H}}(c_l))$$= (S(\theta _{c_l}-),T(\theta _{c_l}-))$,

(A5) :

$\Theta ^{c_k} \preceq \theta \preceq \Theta ^{c_l}$ for some $(c_k,c_l) = B_j$, with $(c_k,{\underline{H}}(c_k)) = (S(\theta _{c_k}-),T(\theta _{c_k}-))$, and $(c_l,{\underline{H}}(c_l)) = (S(\theta _{c_l}),T(\theta _{c_l}))$,

the minimal distribution functions ${\underline{F}}_\theta$ have the following forms

$$\begin{aligned} {\underline{F}}_\theta (x)= & {} \left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\; G(x) \le S(\theta _{c_k}-), \\ \frac{G(x)-S(\theta _{c_k}-)}{S(\theta _{c_l}-)-S(\theta _{c_k}-)}, &{}\quad \mathrm {if}\; S(\theta _{c_k}-)\le G(x) \le S(\theta _{c_l}-), \\ 1, &{}\quad \mathrm {if}\; G(x) \ge S(\theta _{c_l}-), \end{array} \right. \end{aligned}$$

(5.15)

$$\begin{aligned} {\underline{F}}_\theta (x)= & {} \left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\; G(x) \le S(\theta _{c_k}), \\ \frac{G(x)-S(\theta _{c_k})}{S(\theta _{c_l}-)-S(\theta _{c_k})},\;\; &{}\quad \mathrm {if}\; S(\theta _{c_k})\le G(x) \le S(\theta _{c_l}-), \\ 1, &{}\quad \mathrm {if}\; G(x) \ge S(\theta _{c_l}-), \end{array} \right. \end{aligned}$$

(5.16)

$$\begin{aligned} {\underline{F}}_\theta (x)= & {} \left\{ \begin{array}{ll} 0, &{}\quad \mathrm {if}\; G(x) \le S(\theta _{c_k}-), \\ \frac{G(x)-S(\theta _{c_k}-)}{S(\theta _{c_l})-S(\theta _{c_k}-)},\;\; &{}\quad \mathrm {if}\; S(\theta _{c_k}-)\le G(x) \le S(\theta _{c_l}), \\ 1, &{}\quad \mathrm {if}\; G(x) \ge S(\theta _{c_l}), \end{array} \right. \end{aligned}$$

(5.17)

respectively. Assumptions (A1)–(A5) guarantee that the family of distribution functions described in (5.13)–(5.17) is defined for all $\theta \in {\mathbb {R}}$. For verifying that this is stochastically ordered it suffices to refer to formulae (5.8)–(5.12). They show that for ${\underline{F}}_\theta (x)$ is decreasing in $\theta$ every fixed $x \in {\mathbb {R}}$.

The proof of the right-hand side inequality in (2.1) as well as its optimality is analogous to the above, and therefore it is omitted. $\square$