Analytic Solutions to Determine Critical Magnetic Fields for Thermoelectric Magnetohydrodynamics in Alloy Solidification

Abstract

During alloy solidification, it has been observed that the morphology of microstructures can be altered by applying an external DC magnetic field. This structural change can be attributed to solutal convective transport introduced by thermoelectric magnetohydrodynamics (TEMHD) which drives fluid motion within the inter-dendritic region. Complex numerical models with grid resolutions on the microscopic scale have been constructed to solve the equations governing TEMHD. To complement these computationally intensive numerical models, analytic solutions were sought. Specifically, the analytic solutions presented herein are asymptotic solutions derived for TEMHD under low and high magnetic field intensities. Combination of these asymptotic solutions leads to simple formulae for estimating critical magnetic fields which can be readily evaluated in terms of characteristic lengths of materials that have been identified in experiments as key parameters of critical fields. Indeed, the critical magnetic fields predicted with the asymptotic solutions exhibit magnitudes consistent with those applied in current ongoing experiments where significant changes in microstructure have been observed. The capability to predict accurate results indicates that the analytic solutions described herein are valuable precursors not only for detailed numerical simulations but also for experimental design to study critical magnetic fields in alloy solidification.

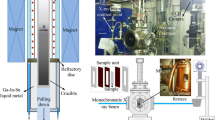
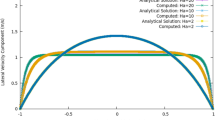
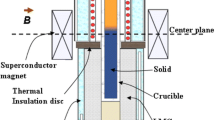
Appendix

1.1 Derivation of Transverse Magnetic Field Solutions

Under a transverse field, the thermoelectric force is

$$\begin{aligned} {\mathbf{J}} \times {\mathbf{B}} = \left| \begin{array}{ccc} \hat{x} &{} \hat{y} &{} \hat{z}\\ 0 &{} 0 &{} J_z \\ 0 &{} B_y &{} 0 \end{array}\right| = -J_z B_y \hat{x} . \end{aligned}$$

(87)

1.1.1 Transverse low field solution

For a low magnetic field ${\mathbf{B}}_{\mathbf{0}}$, the Navier–Stokes equation reduces to

$$\begin{aligned} -J_z B_0 + \mu \frac{\partial ^2 u}{\partial y^2} - \frac{\partial p}{\partial x} = 0 . \end{aligned}$$

(88)

The boundary conditions for the secondary duct are

$$\begin{aligned} \left. u_1 \right| _{y=W_{\text{s}}}&= 0 ,\end{aligned}$$

(89)

$$\begin{aligned} \left. \frac{\partial u_1}{\partial y} \right| _{y=0}&= 0 ,\end{aligned}$$

(90)

$$\begin{aligned} \left. \frac{\partial }{\partial y}\frac{\partial p_1}{\partial x} \right| _{y=0}&= 0 \end{aligned}$$

(91)

and in the primary duct

$$\begin{aligned} \left. u_2 \right| _{y=W_{\text{p}}}&= u_{\text{w}} ,\end{aligned}$$

(92)

$$\begin{aligned} \left. \frac{\partial u_2}{\partial y} \right| _{y=0}&= 0 ,\end{aligned}$$

(93)

$$\begin{aligned} \left. \frac{\partial u_2}{\partial y} \right| _{y=W_{\text{p}}}&= 0 ,\end{aligned}$$

(94)

$$\begin{aligned} \left. \frac{\partial }{\partial y}\frac{\partial p_2}{\partial x} \right| _{y=0}&= 0 ,\end{aligned}$$

(95)

$$\begin{aligned} \left. \frac{\partial }{\partial y}\frac{\partial p_2}{\partial x} \right| _{y=W_{\text{p}}}&= 0 \end{aligned}$$

(96)

where $u_{\text{w}}$ is the velocity at the symmetry boundary. Conservation of mass is given by

$$\begin{aligned} \int _{y=0}^{y=W_{\text{s}}} u_1 {\text{d}}y = \int _{y=0}^{y=W_{\text{p}}} u_2 {\text{d}}y . \end{aligned}$$

(97)

Pressure is continuous along the center of each duct but is constrained by the periodic boundary conditions which requires negative and positive gradients for the secondary and primary ducts respectively. Assuming constant gradients within each duct, the continuity and periodic conditions for pressure can be expressed as

$$\begin{aligned} \left. \frac{\partial p_1}{\partial x}\right| _{y=0} W_r + \left. \frac{\partial p_2}{\partial x}\right| _{y=0} \left( W_{\text{p}} - W_r \right) = 0 . \end{aligned}$$

(98)

The general solutions for pressure and velocity at these two points are

$$\begin{aligned} u_1&= \sum _{n=0}^\infty A_n y^n ,\end{aligned}$$

(99)

$$\begin{aligned} \frac{\partial p_1}{\partial x}&= \sum _{n=0}^\infty C_n y^n ,\end{aligned}$$

(100)

$$\begin{aligned} u_2&= \sum _{n=0}^\infty D_n y^n ,\end{aligned}$$

(101)

$$\begin{aligned} \frac{\partial p_2}{\partial x}&= \sum _{n=0}^\infty E_n y^n . \end{aligned}$$

(102)

In view of the symmetry about the plane at $y=0$, only even integers of n are relevant. The minimum n required to represent the flow profile is determined by the number of critical points imposed by the boundary conditions. For the secondary duct, $n = 2$ which represents parabolic flow. Dimensional analysis of Eq. [88] shows that Eqs. [99] and [100] simplify to Poiseuille flow.

$$\begin{aligned} u_1&= A_0 + A_2 y^2 ,\end{aligned}$$

(103)

$$\begin{aligned} \frac{\partial p_1}{\partial x}&= C_0. \end{aligned}$$

(104)

In the primary duct, the symmetry conditions in Eqs. [94] and [96] at $y = W_{\text{p}}$ imply that there are least three critical points for both the pressure gradient and velocity. Using the pressure gradient as the constraint for minimum n, Eqs. [101] and [102] reduce to

$$\begin{aligned} u_2&= D_0 + D_2 y^2 + D_4 y^4 + D_6 y^6 ,\end{aligned}$$

(105)

$$\begin{aligned} \frac{\partial p_2}{\partial x}&= E_0 + E_2 y^2 + E_4 y^4 . \end{aligned}$$

(106)

Substituting these solutions into Eq. [88] gives

$$\begin{aligned} 2 \mu A_2 - C_0&= J_z B_0 ,\end{aligned}$$

(107)

$$\begin{aligned} 2 \mu D_2 - E_0&= J_z B_0, \end{aligned}$$

(108)

$$\begin{aligned} y^2 \left( 12 \mu D_4 - E_2 \right)&= 0 ,\end{aligned}$$

(109)

$$\begin{aligned} y^4 \left( 30 \mu D_6 - E_4 \right)&= 0 . \end{aligned}$$

(110)

Continuity becomes

$$\begin{aligned} A_0 W_{\text{s}}&+ \frac{1}{3} A_2 W_{\text{s}}^3 - D_0 W_{\text{p}} - \frac{1}{3} D_2 W_{\text{p}}^3 \\&- \frac{1}{5} D_4 W_{\text{p}}^5 - \frac{1}{7} D_6 W_{\text{p}}^7 = 0 . \end{aligned}$$

(111)

The boundary conditions from Eqs. [89], [92], [94] and [96] give

$$\begin{aligned} A_0 + A_2 W_{\text{s}}^2&= 0 ,\end{aligned}$$

(112)

$$\begin{aligned} D_0 + D_2 W_{\text{p}}^2 + D_4 W_{\text{p}}^4 + D_6 W_{\text{p}}^6&= 0 ,\end{aligned}$$

(113)

$$\begin{aligned} 2 D_2 W_{\text{p}} + 4 D_4 W_{\text{p}}^3 + 6 D_6 W_{\text{p}}^5&= 0 ,\end{aligned}$$

(114)

$$\begin{aligned} 2 E_2 W_{\text{p}} + 4 E_4 W_{\text{p}}^3&= 0 . \end{aligned}$$

(115)

The periodic pressure condition Eq. [98] gives

$$\begin{aligned} C_0 W_r + E_0 \left( W_{\text{p}} - W_r\right) = 0 . \end{aligned}$$

(116)

Solving the above system of equations gives

$$\begin{aligned} A_0&= \frac{1}{2 \mu W_0}\left( -16 J_z B_0 W_{\text{p}}^3 \right. \\& \quad + \left. 147 \mu u_{w} \left( W_{\text{p}}-W_r\right) \right) W_{\text{p}} W_{\text{s}}^2 ,\end{aligned}$$

(117)

$$\begin{aligned} A_2&= \frac{1}{2 \mu W_0}\left( 16 J_z B_0 W_{\text{p}}^3 \right. \\& \quad- \left. 147 \mu u_{\text{w}} \left( W_{\text{p}}-W_r\right) \right) W_{\text{p}} ,\end{aligned}$$

(118)

$$\begin{aligned} C_0&= \frac{1}{W_0} \left( J_z B_0 \left( 16 W_{\text{p}}^3 - 49 W_{\text{s}}^3 \right) \right. \\& \quad- \left. 147\mu u_{\text{w}} W_{\text{p}} \right) \left( W_{\text{p}} - W_r \right) ,\end{aligned}$$

(119)

$$\begin{aligned} D_0&= -\frac{1}{2 \mu W_0} \left( 21 J_z B_0 W_{\text{s}}^3 W_{\text{p}}^3\;+ \right. \\&\left. \mu u_{\text{w}} \left( 31 W_{\text{p}}^3 W_r - 98 W_{\text{p}} W_{\text{s}}^3 + 98 W_r W_{\text{s}}^3 \right) \right) ,\end{aligned}$$

(120)

$$\begin{aligned} D_2&= \frac{49 J_z B_0 W_{\text{s}}^3 W_{\text{p}} + 147\mu u_{\text{w}} W_{\text{p}} W_r}{2 \mu W_0} ,\end{aligned}$$

(121)

$$\begin{aligned} D_4&= -\frac{35 J_z B_0 W_{\text{s}}^3 + 105 \mu u_{\text{w}} W_r}{2 \mu W_{\text{p}} W_0} ,\end{aligned}$$

(122)

$$\begin{aligned} D_6&= \frac{7 J_z B_0 W_{\text{s}}^3 + 21 \mu u_{\text{w}} W_r}{ 2 \mu W_{\text{p}}^3 W_0} ,\end{aligned}$$

(123)

$$\begin{aligned} E_0&= \frac{1}{W_0} \left( J_z B_0 \left( - 16 W_{\text{p}}^3 + 49 W_{\text{s}}^3 \right) \right. \\&\quad+ \left. 147 \mu u_{\text{w}} W_{\text{p}} \right) W_r ,\end{aligned}$$

(124)

$$\begin{aligned} E_2&= -\frac{210 J_z B_0 W_{\text{s}}^3 + 630 \mu u_{\text{w}} W_r}{W_{\text{p}} W_0} ,\end{aligned}$$

(125)

$$\begin{aligned} E_4&= \frac{105 J_z B_0 W_{\text{s}}^3 + 315 \mu u_{\text{w}} W_r}{W_{\text{p}}^3 W_0} \end{aligned}$$

(126)

where

$$\begin{aligned} W_0 = 49 W_{\text{s}}^3 \left( W_{\text{p}} - W_r \right) + 16 W_{\text{p}}^3 W_r . \end{aligned}$$

(127)

1.1.2 Transverse high field solution

For a high magnetic field ${\mathbf{B}}_{\infty}$, the damping term reduces to

$$\begin{aligned} \sigma {\mathbf{u}} \times {\mathbf{B}}&= \sigma \left| \begin{array}{ccc} \hat{x} &{} \hat{y} &{} \hat{z}\\ u_x &{} 0 &{} 0 \\ 0 &{} B_y &{} 0 \end{array}\right| = \sigma u_x B_y \hat{z}, \end{aligned}$$

(128)

$$\begin{aligned} \sigma {\mathbf{u}} \times {\mathbf{B}} \times {\mathbf{B}}&= \sigma \left| \begin{array}{ccc} \hat{x} &{} \hat{y} &{} \hat{z}\\ 0 &{} 0 &{} u_x B_y \\ 0 &{} B_y &{} 0 \end{array}\right| \\&= -\sigma u_x B_y^2 \hat{x} . \end{aligned}$$

(129)

The Navier–Stokes equation at $x_1$ and $x_2$ becomes respectively

$$\begin{aligned} -J_z B_{\infty } - \sigma u_1 B_{\infty }^2 - \frac{\partial p_1}{\partial x}&= 0 ,\end{aligned}$$

(130)

$$\begin{aligned} -J_z B_{\infty } - \sigma u_2 B_{\infty }^2 - \frac{\partial p_2}{\partial x}&= 0 . \end{aligned}$$

(131)

Periodic pressure condition gives

$$\begin{aligned} \frac{\partial p_1}{\partial x} W_r + \frac{\partial p_2}{\partial x} \left( W_{\text{p}} - W_r \right) = 0 \end{aligned}$$

(132)

and continuity

$$\begin{aligned} \int _{y=0}^{y=W_{\text{s}}} u_1 {\text{d}}y = \int _{y=0}^{y=W_{\text{p}}} u_2 {\text{d}}y \end{aligned}$$

(133)

reduces to

$$\begin{aligned} u_1 = u_2 \frac{W_{\text{p}}}{W_{\text{s}}} . \end{aligned}$$

(134)

Solving gives

$$\begin{aligned} u_1&= -\frac{J_z W_{\text{p}}^2}{\sigma B_{\infty } W_{\infty }} ,\end{aligned}$$

(135)

$$\begin{aligned} u_2&= -\frac{J_z W_{\text{p}} W_{\text{s}}}{\sigma B_{\infty } W_{\infty }} ,\end{aligned}$$

(136)

$$\begin{aligned} \frac{\partial p_1}{\partial x}&= \frac{J_z B_{\infty }\left( W_r - W_{\text{p}} \right) \left( W_{\text{p}} - W_{\text{s}} \right) }{W_{\infty }} ,\end{aligned}$$

(137)

$$\begin{aligned} \frac{\partial p_2}{\partial x}&= -\frac{J_z B_{\infty } W_r \left( W_{\text{p}} - W_{\text{s}} \right) }{W_{\infty }} ,\end{aligned}$$

(138)

$$\begin{aligned} W_{\infty }&= W_r \left( W_{\text{p}} - W_{\text{s}} \right) + W_{\text{p}} W_{\text{s}} . \end{aligned}$$

(139)

1.2 Derivation of Parallel Magnetic Field Solutions

The Lorentz force for a parellel magnetic field in is given by

$$\begin{aligned} {\mathbf{J}} \times {\mathbf{B}}_{\mathbf{z}} = \left| \begin{array}{ccc} \hat{r} &{} \hat{\theta } &{} \hat{z}\\ J_r &{} J_{\theta } &{} J_z \\ 0 &{} 0 &{} B_z \end{array}\right| = J_{\theta } B_z \hat{r}, -J_r B_z \hat{\theta } \end{aligned}$$

(140)

where $J_r$ is assumed to take a power law in the form of

$$\begin{aligned} J_r = J_0 \left( r^{n-2} - W_{\text{p}}^{n-2} \right) . \end{aligned}$$

(141)

The problem is assumed to be axisymmetric, hence

$$\begin{aligned} \frac{\partial \Psi }{\partial \theta } = \frac{\partial u_{\theta }}{\partial \theta } = \frac{\partial p}{\partial \theta } = 0 . \end{aligned}$$

(142)

It is also assumed that

$$\begin{aligned} \left| \frac{\partial u_{\theta }}{\partial r}\right| >> \left| \frac{\partial u_{\theta }}{\partial z}\right| \approx 0 , \end{aligned}$$

(143)

$$\begin{aligned} \left| \frac{\partial p}{\partial r}\right| >> \left| \frac{\partial p}{\partial z}\right| \approx 0 , \end{aligned}$$

(144)

hence there are no dependencies on $\hat{z}$. From Eq. [142], $J_{\theta } = 0$. The Lorentz force therefore only has component in $\hat{\theta }$. For axisymmetry with no dependency on $\hat{z}$, the continuity equation

$$\begin{aligned} \nabla \cdot {\mathbf{u}} = \frac{1}{r}\frac{\partial r u_r}{\partial r} + \frac{1}{r}\frac{\partial u_{\theta }}{\partial \theta } + \frac{\partial u_z}{\partial z} = 0 . \end{aligned}$$

(145)

becomes

$$\begin{aligned} \nabla \cdot {\mathbf{u}} = \frac{1}{r}\frac{\partial r u_r}{\partial r} = 0 \end{aligned}$$

(146)

which can be solved as

$$\begin{aligned} u_r = \frac{C}{r} \end{aligned}$$

(147)

where C is the constant of integration. Applying the boundary condition

$$\begin{aligned} \left. u_r \right| _{r=r_0} = 0, \end{aligned}$$

(148)

$C = 0$ hence $u_r = 0$ for all r.

1.2.1 Parallel low field solution

For a low magnetic field ${\mathbf{B}}_{\mathbf{0}}$, the Navier–Stokes equation becomes

$$\begin{aligned} -\nabla p + \mu \nabla ^2 {\mathbf{u}} + {\mathbf{J}} \times {\mathbf{B}}_{\mathbf{0}} = 0 . \end{aligned}$$

(149)

For a low Re,

$$\begin{aligned} \frac{{\mathbf{u}}}{r^2} \propto \nabla ^2 {\mathbf{u}} \end{aligned}$$

(150)

implying

$$\begin{aligned} {\mathbf{u}} \propto \nabla p + {\mathbf{J}} \times {\mathbf{B}}_{\mathbf{0}} . \end{aligned}$$

(151)

Therefore with no radial velocity or radial Lorentz force

$$\begin{aligned} \left( \nabla ^2 {\mathbf{u}}\right) \cdot \hat{r} = \frac{\partial p}{\partial r} = 0 \end{aligned}$$

(152)

the problem reduces to a 1-dimensional force balance in $\hat{\theta }$

$$\begin{aligned} &\mu \left( \frac{\partial ^2 u_{\theta }}{\partial r^2} + \frac{1}{r} \frac{\partial u_{\theta }}{\partial r} - \frac{u_{\theta }}{r^2} \right) \\&- J_0 B_0 \left( r^{n-2} - W_{\text{p}}^{n-2} \right) = 0 . \end{aligned}$$

(153)

The general solution of

$$\begin{aligned} \mu \left( \frac{\partial ^2 u_{\theta }}{\partial r^2} + \frac{1}{r} \frac{\partial u_{\theta }}{\partial r} - \frac{u_{\theta }}{r^2} \right) = 0 \end{aligned}$$

(154)

is

$$\begin{aligned} u_\theta = A_1 r + A_2 r^{-1} . \end{aligned}$$

(155)

However, to account for the extra force in Eq. [153], two additional terms were appended to give a particular solution taking the form of

$$\begin{aligned} u_{\theta } = A_1 r + A_2 r^{-1} + A_3 r^n + A_4 r^2 \end{aligned}$$

(156)

where, on the right hand side, the third term accounts for the Lorentz force and the last term ensures the boundary condition of $\left. J_r\right| _{r=W_{\text{p}}}=0$ is satisfied. Substituting into Eq. [153] gives

$$\begin{aligned} \left( \mu \left( n^2 - 1\right) A_3 r^{n-2} - J_0 B_0 r^{n-2}\right) \\ + \left( 3 \mu A_4 + J_0 B_0 W_{\text{p}}^{n-2} \right)&= 0 ,\end{aligned}$$

(157)

$$\begin{aligned} \mu \left( n^2 - 1\right) A_3 r^{n-2} - J_0 B_0 r^{n-2}&= 0 ,\end{aligned}$$

(158)

$$\begin{aligned} \left( 3 \mu A_4 + J_0 B_0 W_{\text{p}}^{n-2} \right)&= 0 . \end{aligned}$$

(159)

Applying the boundary conditions

$$\begin{aligned} \left. u_{\theta }\right| _{r = r_0}&= 0 ,\end{aligned}$$

(160)

$$\begin{aligned} \left. u_{\theta }\right| _{r = W_{\text{p}}}&= 0 \end{aligned}$$

(161)

gives

$$\begin{aligned} A_1 r_0 + A_2 r_0^{-1} + A_3 r_0^n + A_4 r_0^2&= 0 ,\end{aligned}$$

(162)

$$\begin{aligned} A_1 W_{\text{p}} + A_2 W_{\text{p}}^{-1} + A_3 W_{\text{p}}^n + A_4 W_{\text{p}}^2&= 0 . \end{aligned}$$

(163)

Solving the above system of equations gives

$$\begin{aligned} A_1&= \frac{J_0 B_0}{3 \mu \left( n^2 -1\right) \left( W_{\text{p}}^2 - r_0^2 \right) } \left( 3 r_0^{n+1} \right. \\ &\quad -\left. \left( n^2-1 \right) r_0^3 W_{\text{p}}^{n-2} + \left( n^2 - 4 \right) W_{\text{p}}^{n+1}\right) \\&= \frac{J_0 B_0}{\mu } C_1 ,\end{aligned}$$

(164)

$$\begin{aligned} A_2&= \frac{J_0 B_0}{3\mu \left( n^2 -1 \right) \left( W_{\text{p}}^2 -r_0^2 \right) } r_0 \left( -3 r_0^n W_{\text{p}}^2 \right. \\ &\quad+ \left. \left( n^2 - 1 \right) r_0^2 W_{\text{p}}^n - r_0 \left( n^2 - 4 \right) W_{\text{p}}^{n+1} \right) \\&= \frac{J_0 B_0}{\mu } C_2 ,\end{aligned}$$

(165)

$$\begin{aligned} A_3&= \frac{J_0 B_0}{\mu } \frac{1}{\left( n^2 - 1\right) } = \frac{J_0 B_0}{\mu } C_3 ,\end{aligned}$$

(166)

$$\begin{aligned} A_4&= -\frac{J_0 B_0}{\mu } \frac{W_{\text{p}}^{n-2}}{3} = \frac{J_0 B_0}{\mu } C_4 . \end{aligned}$$

(167)

Application of L’Hôpital’s rule as $n \rightarrow -1$

$$\begin{aligned} u_{\theta } =&A_1 r + \left( A_2+A_3\right) r^{-1} + A_4 r^2 ,\end{aligned}$$

(168)

$$\begin{aligned} \displaystyle \lim _{n \rightarrow -1} \left( A_2+A_3 \right)&= -B_0 J_0 \left( 3W_{\text{p}}^3 \ln r_0 + r_0^2\right. \\ &\left. \left( 2r_0 - 2W_{\text{p}} -3W_{\text{p}} \ln W_{\text{p}} \right) \right) / \\&6 \mu W_{\text{p}} \left( r_0^2 - W_{\text{p}}^2 \right) ,\end{aligned}$$

(169)

$$\begin{aligned} \displaystyle \lim _{n \rightarrow -1} A_1&= B_0 J_0 \left( 2 r_0^3 - 2W_{\text{p}}^3\;- \right. \\ &\left. 3r_0^2 W_{\text{p}} \ln r_0 + 3 W_{\text{p}}^3 \ln W_{\text{p}} \right) / \\&6 \mu \left( r_0^2 W_{\text{p}} - W_{\text{p}}^3 \right) \end{aligned}$$

(170)

and as $n \rightarrow 1$

$$\begin{aligned} u_{\theta } =&\left( A_1 + A_3 \right) r + A_2 r^{-1} + A_4 r^2 ,\end{aligned}$$

(171)

$$\begin{aligned} \displaystyle \lim _{n \rightarrow 1} \left( A_1+A_3 \right)&= B_0 J_0 \left( 2r_0^3-2W_{\text{p}}^3 \;- \right. \\ &\left. 3r_0^2W_{\text{p}} \ln r + 3 W_{\text{p}}^3 \ln W_{\text{p}} \right) / \\&6 \mu \left( r_0^2 W_{\text{p}} - W_{\text{p}}^3 \right) ,\end{aligned}$$

(172)

$$\begin{aligned} \displaystyle \lim _{n \rightarrow 1} A_2&= -B_0 J_0 r_0^2W_{\text{p}} \left( 2 r_0 - W_{\text{p}} \right. \\ &\left. \left( -2 -3 \ln r_0 +3 \ln W_{\text{p}} \right) \right) /\\&\left( 6 \mu \left( r_0^2 - W_{\text{p}}^2 \right) \right) \end{aligned}$$

(173)

shows that the velocity remains finite as $\left| n \right| \rightarrow 1$.

1.2.2 Parallel high field solution

For a high magnetic field ${\mathbf{B}}_{\infty}$, Navier–Stokes equation becomes

$$\begin{aligned} -\nabla p + {\mathbf{J}} \times {\mathbf{B}}_{\infty} + {\mathbf{u}} \times {\mathbf{B}}_\infty \times {\mathbf{B}}_\infty = 0 . \end{aligned}$$

(174)

With no radial velocity or radial Lorentz force

$$\begin{aligned} {\mathbf{u}} \times {\mathbf{B}}_{\infty} \times {{\mathbf{B}}_\infty}_r = {\mathbf{J}} \times {{\mathbf{B}}_\infty}_r = \frac{\partial p}{\partial r} = 0 \end{aligned}$$

(175)

and Eq. [174] reduces to a force balance in $\hat{\theta }$

$$\begin{aligned} -J_r B_{\infty } - \sigma u_{\theta } B_{\infty }^2 = 0 . \end{aligned}$$

(176)

Substituting $J_r$ from Eq. [141] gives

$$\begin{aligned} u_{\theta } = - \frac{J_0 \left( r^{n-2} - W_{\text{p}}^{n-2} \right) }{\sigma B_{\infty }} . \end{aligned}$$

(177)