Measuring Stress Distributions in Ti-6Al-4V Using Synchrotron X-Ray Diffraction

Abstract

This article presents a quantitative strain analysis (QSA) study aimed at determining the distribution of stress states within a loaded Ti-6Al-4V specimen. Synchrotron X-rays were used to test a sample that was loaded to a uniaxial stress of 540 MPa in situ in the A2 experimental station at the Cornell High Energy Synchrotron Source (CHESS). Lattice-strain pole figures (SPFs) were measured and used to construct a lattice strain distribution function (LSDF) over the fundamental region of orientation space for each phase. A high-fidelity geometric model of the experiment was used to drastically improve the signal-to-noise ratio in the data. The three-dimensional stress states at every possible orientation of each α (hcp) and β (bcc) crystal within the aggregate were calculated using the LSDF and the single-crystal moduli. The stress components varied by 300 to 500 MPa over the orientation space; it was also found that, in general, the crystal stress states were not uniaxial. The maximum shear stress resolved on the basal and prismatic slip systems of all orientations within the α phase, $\hat \tau _{{\text{rss}}} ,$ was calculated to illustrate the utility of this approach for better identifying “hard” and “soft” orientations within the loaded aggregate. Orientations with low values of $\hat \tau _{{\text{rss}}} ,$ which are potential microcrack initiation sites during dwell fatigue conditions, are considered hard and were subsequently illustrated on an electron backscatter diffraction (EBSD) map.

1 Introduction

Newly developed synchrotron X-ray diffraction techniques are changing the manner in which we test the microstructure and, indeed, the micromechanical state within deforming polycrystalline metallic specimens. The combination of rapid collection times and the ability to observe many scattering vectors simultaneously facilitates the performance of thermomechanical processing and performance-like experiments in situ. Experimental techniques have been developed toward this end, to observe both “bulk” populations[1–3] and individual embedded grains.[4–7] The data from such experiments can provide an unparalleled level of detail regarding the evolution of micromechanical states during deformation processes.

Perhaps the most important product from these experiments is the increased understanding of grain-scale deformation partitioning. The measured distributions of crystal (lattice) strains and the related stresses describe the micromechanical state and can be employed to understand important phenomena such as crack initiation and phase transformation. At the scale of statistically representative volumes, these distributions are expected to display a nontrivial orientation dependence. Furthermore, the crystal strains/stresses may in general be quite different from the macroscopic quantities; as such, maximizing the number of independent strain measurements is generally necessary, to best quantify the micromechanical state. Motivated by quantitative texture analysis (QTA), our group has developed a synchrotron X-ray diffraction method for measuring lattice strain pole figures (SPFs). The challenge of such quantitative strain analysis (QSA) experiments is to maximize the number of SPFs measured and the amount of data on each. By employing in-situ mechanical loading, sets of SPFs are acquired at various macroscopic stress values.[3] The SPF data from a polycrystalline aggregate are inverted to form a lattice strain distribution function (LSDF), which is employed within Hooke’s law to calculate the orientation-dependent stress tensor, σ( R ), for every crystal orientation, R , within the aggregate.[8] Previous QSA studies have demonstrated the strong link between σ( R ) and the crystal orientation distribution function (ODF)[9] and have shown a strong correlation between σ( R ) data and crystal-based finite element results.[10] The latter study demonstrated that, even though the stresses computed in the finite element method (FEM) simulation included local effects such as the influence of a crystallographic neighborhood, the orientation-averaged FEM stress distribution compared very well with the experimental σ( R ) results.

In this article, we describe a QSA study aimed at understanding deformation partitioning in Ti-6Al-4V, an important titanium alloy. The large elastic strains and anisotropic single-crystal properties of this alloy make it an ideal and interesting material for these experiments. In the following sections, we describe the study material and experimental method. We focus here on the details of the diffraction data reduction routine that we employ to derive lattice strains from area detector data. We then present the experimental results and demonstrate the utility of the σ( R ) analysis for understanding micromechanically “at-risk” orientations.

2 Material and experiments

The in-situ mechanical tests and synchrotron X-ray experiments performed here for the measurement of SPFs are identical to those described in Reference 3. The experiments were conducted at the A2 experimental station at the Cornell High Energy Synchrotron Source (CHESS). In this section, we describe the study material and present the basics of the experimental method.

2.1 Material

The material selected for this study was commercially available Ti-6Al-4V plate in a nominal mill annealed condition. The microstructure, as depicted in the backscatter electron micrographs shown in Figure 1, consisted of a bimodal size distribution of equiaxed α (hcp) grains delineated by a relatively small volume fraction (6.5 pct) of β (bcc) phase. The peaks in the α grain-size distribution occur at 9.5 μm and 1.1 μm. The composition of each phase and the overall alloy were estimated by standardless energy-dispersive spectroscopy. The composition of the α and β phases (in weight percentages) was Ti-8.1Al-1.3V and Ti-2.6Al-14.5V, respectively, which were obtained by collecting spot scans from each phase individually. The alloy composition, acquired using a full-frame scan from an area of 2400 μm² was Ti-7.3Al-3.2V. The ODF of each phase, as determined by a Rietveld analysis of the synchrotron X-ray diffraction data,[11,12] is shown in Figure 2, over the associated fundamental zones of the orientation space. We employ the Rodrigues parameterization, ${\mathbf{r}}={\mathbf{n}}{\text{ tan}}\frac{\phi } {2},$ where n and ϕ are the axial and angular invariants of the associated rotation.[13] The unit cell axes are attached to the orientation frame using the conventions described by Nye.[14] We define a Cartesian coordinate system on the specimen, so that loading-transverse-normal specimen directions (LD-TD-ND) correspond to x-y-z. The slices shown in Figure 2 are taken perpendicular to a vector along the ND || z direction. The maximum ODF values of 6 to 7 multiples of a uniform distribution (MUD) indicate a moderately strong preferred orientation in both phases.

Fig. 1

Backscattered electron micrographs of the microstructure of the as-received Ti-6Al-4V. Dark regions are the α (hcp) phase and lighter regions are the β (bcc) phase

Fig. 2

(a) ODF for the α-Ti (hcp) shown on slices from the hexagonal Ω _fr taken along the ND; (b) ODF for the β-Ti (bcc) phase. The scale for each ODF is in MUD. A uniform ODF has a MUD value of 1 everywhere

Electron backscatter diffraction (EBSD) scans were performed in a scanning electron microscope (SEM) equipped with a field emission source and an automated EBSD acquisition system. The SEM was operated at an accelerating voltage of 20 kV and a beam current of 2.39 nA. The EBSD scans were acquired with the sample tilted to 70 deg at a working distance of 21 mm. The first scan was acquired at a step size of 1 μm; it provided the grain-size distribution information and verified the X-ray-based ODFs depicted in Figure 2. Orientation and grain-boundary data from a more highly resolved scan (350-nm step size) are shown in Figure 3. The orientation variation is apparent even within grains. An extensive network of low-angle boundaries (2 to 15 deg) accommodates the change in orientation over the larger grains, while high angle boundaries (>15 deg) are present between the finer-scale grains (Figure 3).

Fig. 3

(a) Colored orientation map of the EBSD data plotted relative to the ND (which is parallel to the sample polished ND). The inverse pole figures describe the color map. (b) Misorientation boundaries for the angular ranges shown for the blue, red, and green lines

2.2 In-Situ Synchrotron X-Ray Experiments

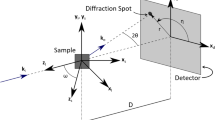
The experimental setup, shown schematically in Figure 5, included a mechanical testing frame with precise specimen alignment, a single-axis goniometer for specimen positioning, and a Mar345¹ online image plate detector.[3] The tensile specimen, shown in Figure 4(a), was taken from the Ti-6Al-4V sheet, so that the LD was parallel to the original rolling direction, and the TD and ND corresponded to the original TD and ND, respectively. Uniaxial deformation was applied along the specimen x axis; hence, the only nonzero macrostress component in the specimen frame is S _xx  = P/A, where P is the applied axial load and A is the cross-sectional area. The macroscopic stress-strain response of the Ti-6Al-4V is shown in Figure 4(b).

Fig. 4

(a) Tensile specimen employed in the mechanical loading/diffraction experiments. The LD and TD are depicted. The ND is through the specimen thickness. All dimensions are in millimeters. (b) Macroscopic stress-strain curve for the Ti-6Al-4V specimen loaded in tension. The two discrete points on the curve at 0 and 540 MPa depict macroscopic stress values at which the diffraction experiments were conducted

The in-situ diffraction experiment involves collecting diffraction data for several specimen orientations at a series of prescribed (constant) macroscopic stress levels. A square 0.5-mm beam of 50 keV X-rays was used to illuminate a volume of grains near the center of the tensile specimen in transmission (Laue) geometry. Additionally, a paste of CeO₂ powder² was applied to the specimen’s downstream face, to provide a fiducial point in each image. The statistical relevance of the diffraction volume was verified by the texture analysis, as discussed in References 8 and 9. The SPFs were collected for applied loads of 0 and 540 MPa, using five images each, measured for ω ∈ [−30, −15, 0, 15, and 30 deg]. The detector was positioned to capture Bragg reflections³ down to ∼1 Å, which encompassed 10 from CeO₂ (fcc), 11 from α-Ti (hcp), and 4 from β-Ti (bcc).

Area detectors facilitate SPF measurements by collecting entire Debye rings for many {hkl} simultaneously.[3,8,9] Figure 6 depicts a typical diffraction image from the Ti-6Al-4V experiments. It is natural to use a polar coordinate system, (ρ′, η′), centered on the transmitted beam, to describe pixel coordinates (Figure 5). Lattice strains are manifested on the detector as radial shifts of the Bragg peaks, in response to the applied stress. In the presence of deviatoric strains, these shifts will have an azimuthal dependence.

Fig. 5

Schematic of the diffraction experiment, denoting the X-ray beam, specimen, and detector, as well as several relevant coordinate systems

The radial detector coordinate is related to the Bragg angle via the instrument geometry, which is discussed further in Section III. For a fixed X-ray wavelength, λ, the Bragg angle is related to the spacing of an associated set of crystallographic planes through Bragg’s law:

$$ \lambda = 2\bar d_{\mathbf{c}} \sin \theta _{\mathbf{c}} $$

(1)

where $\bar d_{\mathbf{c}}$ is the mean spacing for the crystallographic family, c ⊥ {hkl}, in the subset of grains satisfying a Bragg condition. If we write the sample relative-scattering vector associated with a diffracted beam as s, the Bragg condition can be written

$$\hbox{R}^{\ast} \mathbf{c}=\pm\mathbf{s}$$

(2)

where R ^* represents a one-parameter family of orientations known as a fiber.[15] The shorthand notation, c || s is often used to represent Eq. [2] in the literature. The normal (lattice) strain along c associated with the measured s may then be defined as

$$ {\tilde\epsilon}_{\mathbf{c}} ({\mathbf{s}}) \equiv\frac{{\bar d_{\mathbf{c}} - d_{\mathbf{c}}^0 }} {{d_{\mathbf{c}}^0 }} $$

(3)

where $d_{\mathbf{c}}^0$ is the reference plane spacing, typically calculated from annealed-state lattice parameters. Equation [3] defines the SPF. In the present context, c is the label, and s is the domain (i.e., the unit sphere). Note that this definition implies antipodal symmetry in ${\tilde\epsilon}_{\mathbf{c}} ({\mathbf{s}})$.

Individual radial spectra for distinct values of η′ are produced by performing a polar rebinning of the diffraction image, referred to as “caking.”[16] An example radial spectrum using an azimuthal bin size of Δη′ = 15 deg is shown in Figure 6 (right). The radial spectra for each η′ bin are subsequently converted to angular spectra, using the instrument geometry to convert ρ′ → 2θ (Section III). Lattice-strain data may finally be extracted from the measured 2θ positions of the Bragg peaks in these angular spectra, and assigned to the appropriate SPF.

Fig. 6

(Left) A powder-diffraction image obtained from the Ti-6Al-4V sheet. The beam energy was ∼50 keV and the sample-to-detector distance was ∼67 cm (Table III). The boundaries of a typical integration sector are shown. (Right) The radial spectrum resulting from the sector integration (caking) of the image at the left using Fit2d

3 Data reduction

The values of 2θ _c are typically measured by fitting an analytic profile function, e.g., pseudo-Voigt, to the peaks in the 2θ spectra. The ability to match the observed and predicted positions of the Bragg peaks with high fidelity is the central task in QSA. However, uncertainties in the instrument geometry and any distortion intrinsic to the detector produce systematic variations in the radial positions of the Bragg peaks, just as strain does. For this reason, all sources of spatial distortions in the diffraction instrument must be quantified a priori, using a strain-free standard, and subsequently deconvolved from the data. While simplified methods, such as approximating each ring as an ellipse, have been employed to fit strained powder patterns with satisfactory results,[1,2] a more sophisticated, self-consistent method is necessary for generating SPFs for LSDF analysis.[3,8] Our approach is to first correct the raw detector data, using the fiducial CeO₂ pattern, and then fit the η-dependent 2θ spectra from the diffraction pattern to the analytic profile functions. To accomplish this, an accurate geometric model of the diffraction instrument is necessary, as is a method for “unwarping” the raw images, as necessary.

We describe the key points of our data reduction methodology in this section. We begin with the geometric model we employ for the experiment and the way it is employed to correct our raw diffraction data. The scheme we use to calculate lattice strain and to determine SPFs is then described.

3.1 Instrument Geometry

Powder-diffraction images represent the intersection of the Debye–Scherrer cones with the detector plane, as depicted in Figure 7. As such, the geometry of conic sections may be used to understand the effects of a tilted detector on the detector-relative coordinates, ($\hat \rho ^{\prime \prime} ,\hat \eta^{\prime \prime}$), for a strain-free pattern (i.e., the CeO₂).

Fig. 7

Schematic of the synchrotron X-ray instrument geometry. All CSs are defined relative to a laboratory frame in which the X-ray beam is fixed. The scattering center of the sample defines the origin of the reference coordinate system, {X, Y, Z}. The intersection of the beam and the detector plane defines the origins of the ideal detector CS, {X′, Y′, Z′} and the tilted detector CS, {X′′, Y′′, Z′′}. Note that {X′, Y′, Z′} is “ideal” in the sense that the X′ – Y′ plane is orthogonal to the X-ray beam. The inset illustrates the distortion of the Debye ring on the image plane as a result of the detector tilt. Also shown is the radial integration CS, $\left\{ {{\mathbf{\hat X}}^{\prime \prime} {\text{, }}{\mathbf{\hat Y}}^{\prime \prime} ,{\mathbf{\hat {\rm Z}}}^{\prime \prime} } \right\}$, which, in general, may be displaced from {X′′, Y′′, Z′′} in the detector plane by vector t

The instrument geometry for our experimental setup may be effectively modeled by the following four coordinate systems (CSs):

• (1) the reference CS, {X, Y, Z};

• (2) the ideal detector CS, {X′, Y′, Z′};

• (3) the tilted detector CS, {X′′, Y′′, Z′′}; and

• (4) the integration or raw CS, $\left\{ {{\mathbf{\hat X}}^{\prime \prime} {\text{, }}{\mathbf{\hat Y}}^{\prime \prime} ,{\mathbf{\hat {\rm Z}}}^{\prime \prime} } \right\}$.

These systems are depicted schematically in Figures 5 and 7. These four coordinate systems are related by the following transformations:

$$ \left\{ {{\mathbf{X}}^\prime ,{\text{ }}{\mathbf{Y}}^\prime ,{\text{ }}{\mathbf{Z}}^\prime } \right\}{\text{ }} = \left\{ {{\mathbf{X}},{\text{ }}{\mathbf{Y}},{\text{ }}{\mathbf{Z}}} \right\} - \left\lfloor {0,\,0,\,{\text{D}}} \right\rfloor $$

(4)

$$ \{ {\mathbf{X}}^{\prime \prime } {\text{, }}{\mathbf{Y}}^{\prime \prime } {\text{, }}{\mathbf{Z}}^{\prime \prime } \} = {\text{R}}(\gamma_{{\mathbf{X}}^{\prime \prime }} {\mathbf{X}}^{\prime \prime } ) {\cdot} {\text{R}}(\gamma_{{\mathbf{Y}}^\prime} {\mathbf{Y}}^\prime ) {\cdot} \{ {\mathbf{X}}^\prime {\text{, }}{\mathbf{Y}}^\prime {\text{, }}{\mathbf{Z}}^\prime \} $$

(5)

$$ \left\{ {{\mathbf{\hat X}}^{\prime \prime } {\text{, }}{\mathbf{\hat Y}}^{\prime \prime } {\text{, }}{\mathbf{\hat Z}}^{\prime \prime } } \right\} = \left\{ {{\mathbf{X}}^{\prime \prime } {\text{, }}{\mathbf{Y}}^{\prime \prime } {\text{, }}{\mathbf{Z}}^{\prime \prime } } \right\} + \left\lfloor {{\mathbf{t}}_1 ,\,{\mathbf{t}}_2 ,0} \right\rfloor , $$

(6)

where D is the sample to detector distance and the notation R (ϕ n) represents the rotation matrix corresponding to a rotation through angle ϕ about the axis n. The integration CS, $\left\{ {{\mathbf{\hat X}}^{\prime \prime} {\text{, }}{\mathbf{\hat Y}}^{\prime \prime} {\text{, }}{\mathbf{\hat Z}}^{\prime \prime} } \right\}$, represents the caking coordinate system; its origin represents the initial estimate of the theoretical pattern center. The true pattern center is coincident with the origins of both {X′′, Y′′, Z′′} and {X′, Y′, Z′}. Note that rotations about the detector normal are not considered for several reasons: they only affect the baseline definition of $\hat \eta^{\prime \prime}$, they are the easiest to minimize in the instrument setup, and they typically cannot be determined using powder-diffraction images.

3.2 Correcting for Image Distortion

Image distortion can be attributed to two sources: instrument geometry and intrinsic detector distortions. Table I lists the instrument parameters consistent with our experimental setup and geometric model. It is generally difficult to deconvolve the various causes of image distortion independently. As a result, the only feasible approach is generally via optimization, i.e., the relevant instrument and material parameters are iteratively adjusted (refined), to minimize some objective function based on the errors between the observed and calculated spectra. In this manner, a diffraction image from a strain-free calibrant material, such as powdered Si, LaB₆, or CeO₂, can be used to estimate the following:

• (a) the X-ray wavelength, λ (or equivalently, energy, E);

• (b) the coordinates of the pattern center (components of t);

• (c) the sample-to-detector distance, D;

• (d) the detector nonorthogonality parameters (γ _Y′ and γ _X′′); and

• (e) the radial component of the intrinsic detector distortion,⁴ $\delta _{\hat \rho \prime \prime }$.

Table I Instrument Parameters Describing the Monochromatic Diffraction Setup with a Two-Dimensional Area Detector*

Once these parameters are obtained, correction of the diffraction data acquired during the in-situ experiments becomes a matter of transforming the detector coordinates of the raw intensity data, ($\hat \rho ^{\prime \prime} {\text{, }}\hat \eta ^{\prime \prime}$) to (ρ′, η′), and converting ρ′ → 2θ. The procedure is performed algorithmically, as follows.

• (1) Apply $\delta _{\hat \rho ^{\prime \prime} }$ to $\hat \rho ^{\prime \prime}$.

• (2) Transform ($\hat \rho ^{\prime \prime} {\text{, }}\hat \eta ^{\prime \prime}$) to (ρ′′, η′′), using t.

• (3) Transform (ρ′′, η′′) to d′′ = ⌊x′′, y′′, z′′⌋.

• (4) Transform d′′ → d′ = ⌊x′, y′, z′⌋, using R (γ _X′′ X′′) and R(γ _Y′ Y′).

• (5) Transform d ′ → d = ⌊x, y, z⌋, using D.

• (6) Calculate 2θ from d as arccos (−Z·d).

Because the beam, and possibly the detector, can move slightly over the course of the experiment, it is necessary to have a fiducial point in each image. We accomplish this by applying a calibrant powder to the downstream face of the specimen, as described in Section II–B and Eq. [3]. This allows for the subsequent refinement of instrument parameters, as necessary.

The calculation of 2θ _c requires knowledge of the lattice parameters and indices, c ⊥ {hkl}, associated with each peak, along with the wavelength of the incident radiation. When using a layer of calibrant material on the specimen, as described earlier, the offset in scattering centers between the two materials must also be accounted for. This is done with an offset parameter, δ _D , which may be interpreted as the distance along the X-ray beam between the sample and calibrant scattering centers. This can be incorporated into a forward-modeling approach such as Rietveld refinement, which has the benefit of intrinsically accounting for overlapping peaks. This can be particularly important for the study of multiphase samples such as Ti-6Al-4V, in which some degree of overlap between the low-order calibrant and sample reflections is to be expected.

3.3 Fitting Corrected Data

Powder-diffraction spectra may generally be modeled as a superposition of sharp Bragg peaks and a smoothly varying background. Analytic profile functions are used to extract information from these spectra, such as the positions and integrated intensities of the various Bragg peaks. While the procedure of fitting these analytic functions to diffraction spectra may be approached in different ways, its primary objective is to minimize a weighted residual of the form

$$ R_y = \sum\limits_{i = 1}^{N_\rho } {w_i (y_i^{{\text{obs}}} - y_i^{{\text{cal}}} )^2 } $$

(7)

where $y_i^{{\text{obs}}}$ and $y_i^{{\text{cal}}}$ are the observed and calculated intensities for the ith angular bin, and w _i is the weight. The weights in Eq. [7] are set to $w_i = \frac{1} {{y_i^{{\text{obs}}} }}$, as is the case in the standard Rietveld method.[17,18]

For problems in QTA and QSA, sets of spectra, each corresponding to different scattering vectors, are often fit simultaneously. Many analytic functions have been proposed for modeling diffraction spectra. In the present work, a pseudo-Voigt profile function is employed for modeling the Bragg peaks:

$$ y^{pV} (2\theta ) = A(mG(2\theta ) - (1 - m)L(2\theta )) $$

(8)

where A and m are parameters

$$ G(2\theta ) = \exp - \frac{{(2\theta - 2\theta _0 )^2 }} {{2\sigma ^2 }} $$

(9)

and

$$ L(2\theta ) = \frac{{\left( {\frac{\Gamma } {2}} \right)^2 }} {{\left( {\frac{\Gamma } {2}} \right)^2 + (2\theta - 2\theta _0 )^2 }} $$

(10)

While rather simple, this symmetric profile function has been used to successfully model the profiles obtained via synchrotron sources, for a wide variety of cases.[19,20] A simple polynomial is employed to model the background.

The complete calculated intensity profile containing N _c calibrant peaks and N _f “free,” or strained, peaks is then written as

$$ y^{{\text{cal}}} = p^d + \sum\limits_{i = 1}^{N_c } {y_i^{pV} } + \sum\limits_{i = 1}^{N_f } {y_i^{pV^{\ast}} } $$

(11)

where $p^d = \sum\nolimits_{i = 0}^d {a_i (2\theta )^i }$ is the polynomial background function of degree, d. The third term, $y^{pV^{\ast}}$, denotes a pseudo-Voigt function having an additional parameter, $\delta _{2\theta _0 }$, that allows the mean value of the peak, 2θ ₀, to shift by an arbitrary amount associated with the lattice strain for that particular bin. So, 2θ ₀ → 2θ ₀ + $\delta _{2\theta _0 }$, in Eqs. [9] and [10].

In this analysis, the free parameters describing the shape of each peak, A, m, σ, and Γ, as well as the background coefficients, a _i , are fit to data that have been transformed, using the initial guess for the instrument parameters. If the initial guess is sufficiently close to the optimal solution, then the change in profile shapes and background will be negligible. A program such as the freely available Fit2d (European Synchrotron Radiation Facility, Grenoble, France)[16] can be used to obtain a sufficiently accurate initial guess for the center, tilt, and distance values. With the profile shapes tabulated, optimization for the instrument parameters or strain can be undertaken by minimizing R _y (Eq. [7]) for each image. Table II indicates the parameters that remain free, for each type of image. The first set of images is obtained from a special calibrant specimen, i.e., one geometrically identical to the tensile specimen but containing a window filled with CeO₂ powder. Table III gives the final parameter values for each ω setting of the diffractometer. We also acquire images from the unstrained Ti-6Al-4V sample. The lattice parameters can be determined relatively accurately if the residual strains in the sample are below ∼10⁻⁴, which appears to be a valid assumption for the Ti-6Al-4V. Table IV gives the lattice parameters determined from an unstrained Ti-6Al-4V image. Finally, the data from the strained images are adjusted only for beam movement. The lattice strains for each peak are then extracted from the $\delta _{2\theta _0 }$ values from the nonlinear optimization. Figure 8 depicts sections from the Ti-6Al-4V + CeO₂ spectrum, from both unstrained and strained images of scattering vectors aligned with the LD and TD. The shift toward smaller values of 2θ (larger lattice spacing) is consistent for {hkl}s aligned with the LD, with larger values of 2θ consistent with scattering vectors aligned with TD. Note that the calibrant powder peaks remain stationary during deformation, as expected.

Table II Free Parameters during the Fitting of Each Image Type

Table III Optimal Solutions for the Suite of Calibrant and Unstrained Images, Following the Schedule Given in Table II*

Table IV Initial and Refined Lattice Parameters for the Ti-6Al-4V Specimen from the Corrected Reference Image (in Å)*

Fig. 8

Sections of 2θ spectra for the nominal LD and TD sectors. The lattice strains appear as shifts in the α- and β-Ti peaks, which are opposite in direction; the LD and TD spectra are very different in magnitude. (a) η′ = 0 deg (LD) and (b) η′ = 90 deg (TD)

For most synchrotron sources, E should vary by less than 20 to 30 eV over the course of a typical experiment; hence, it is determined by independent means and subsequently fixed. Furthermore, for diffractometers in high energy with large D configurations suitable for strain measurements, there is a high degree of correlation between small changes in the beam energy, D, and lattice parameters. This precludes the ability to refine these parameters simultaneously. The sequence in which these parameters are determined is given in Table II. Similarly, the detector tilt and radial distortion are not physically expected to change. Appropriate values are obtained by averaging the independently refined values from each unstrained image listed in Table III, which are observed to vary little across the images.

The validity of this method, as well as an estimate of achievable strain resolution, can be verified by examining the deviations between the measured and predicted CeO₂ peak positions. Because we used the “piggyback” calibrant scheme, there are several unstrained CeO₂ peaks in each image. The root-mean-square values of the CeO₂ “pseudostrains” in several postprocessed images were observed to be ∼5 × 10⁻⁵, with maximum magnitudes of ∼1 × 10⁻⁴. There was no discernible ρ or η dependence in the pseudostrain data, which implies the absence of any remaining systematic errors. Because the peak widths for the CeO₂ and Ti (both phases) are on the same order, a conservative estimate of this method’s strain resolution for individual peaks is ∼1 × 10⁻⁴. This is consistent with the reports for similar experimental setups.

4 Results

As described in detail in Reference 3, the lattice strains extracted from the diffraction data were plotted on lattice SPFs. Experimental lattice-strain data for a macroscopic stress value of 540 MPa are shown in Figure 9 for the α phase and Figure 10 for the β phase.

Fig. 9

Selected SPFs from the α phase of the Ti-6Al-4V specimen loaded to a macroscopic stress level of 540 MPa. The experimental SPFs are labeled as input and the recalculated SPFs projected from the LSDF are labeled as inverted. Both the glyph color and size represent the associated lattice-strain values. The relative percent errors for strains above the respective mean values between the input and recalculated (inverted) SPFs were ∼10 pct

Fig. 10

Selected SPFs from the β phase of the Ti-6Al-4V specimen loaded to a macroscopic stress level of 540 MPa. The relative percent errors for strains above the respective mean values between the input and recalculated (inverted) SPFs were ∼10 pct

4.1 Distribution of Crystal Stresses, σ( R )

Details regarding the determination of $\epsilon$ and σ can be seen in References 8 and 9. Only the details most germane to the current work are presented here. The first step is the determination of LSDF from the SPF data.[8] Basically, the LSDF, $\epsilon$( R ), represents the average lattice (elastic) strain tensor for the volume fraction of the polycrystal near the orientation, R . The macroscopic elastic strain, $\bar \epsilon$, is obtained by integrating the LSDF weighted by the ODF, f( R ), over the orientation space; i.e.,

$$ \bar \epsilon = \int\limits_{\Omega fr} {\epsilon ({\textsf{R}})f({\textsf{R}})d{\textsf{R}}} $$

(12)

While the LSDF is not a probability distribution function, the relationship between the $\epsilon$( R ) and the SPFs is directly analogous to the fundamental relationship of QTA between the ODF and pole density figures.[15] As described in detail elsewhere,[8,9] we employ a constrained optimization framework to determine the LSDF from N SPFs, using the following objective function:

$$\mathop{\min}\limits_{\epsilon}\left(\sum\limits_{i = 1}^N {\parallel\tilde P_{{\mathbf{c}}_i}{\tilde{\epsilon}}_{{\mathbf{c}}_i}^M - \tilde P_{{\mathbf{c}}_i } {\tilde{\epsilon}}_{{\mathbf{c}}_i }^R \parallel ^2 + \xi {\cdot} \parallel \nabla{\epsilon}\parallel _{\Omega _{fr} }^2 \kappa {\cdot}\parallel \nabla {\hbox{Tr}\tilde{\epsilon}}\parallel _{\Omega_{fr}}^2}\right)$$

(13)

subject to

$$ \sigma ^{\text{a}} - \delta _\sigma \le \frac{1} {{V_\Omega }}\int\limits_{V_\Omega } {{\mathbb{C}}_{1_j \epsilon _j } f\,d{\textsf{R}} \le \sigma ^{\text{a}} + \delta _\sigma } $$

(14)

$$ \frac{1} {{V_\Omega }}\int\limits_{V_\Omega } {{\mathbb{C}}_{ij} \epsilon _j fd{\textsf{R}} = 0} $$

(15)

For ξ, κ ≥ 0, i = 2, 3, 4, 5, 6 and j = 1, 2, 3, 4, 5, 6, where $\tilde P_{{\mathbf{c}}_i }$ are the pole figures determined from the ODF, f, and δ _σ is a suitable tolerance on the applied stress magnitude, here chosen as 5 MPa.

In addition to requiring coincidence between the measured lattice strains, ${{\tilde \epsilon }}_{\mathbf{c}}^M$, and those recalculated from the LSDF, ${{\tilde \epsilon }}_{\mathbf{c}}^R$, we also penalize gradients in the LSDF and dilation over the orientation space with the second and third terms, respectively, in Eq. [13]. Guidelines related to the choice of the weighting parameters ξ and κ are discussed in detail in Reference 8. For the Ti-6Al-4V data, we employed values of ξ = 0.05 and κ = 100, for both phases.

The constraints based on the macroscopically applied stress, Eqs. [14] and [15], were first introduced by Bernier et al.[9] In the case of a multiphase system, their application becomes slightly more ambiguous. Because the α phase accounts for 93.5 pct of the volume and percolates completely through the sample, as seen in Figure 1, however, we felt justified in assuming that its calculated macrostress should be constrained to match the applied value closely. Due to its uniform distribution, the β phase was also constrained to match the applied stress.

Both the measured SPFs and the SPFs recalculated from the LSDFs for the α and β phases are depicted in Figures 9 and 10, respectively.

The main utility of the LSDF is for the calculation of σ( R ); this calculation is done using linear elasticity (i.e., Hooke’s law):

$$ \sigma ({\textsf{R}}) = {\mathbb{C}}({\textsf{R}})\epsilon ({\textsf{R}}) $$

(16)

Here, ${\mathbb{C}}$( R ) is the elastic stiffness tensor evaluated at each crystal orientation, R . Components of the crystal stress distributions for the α and β phases, written in the sample frame, are shown in Figures 11 and 12, respectively. The elastic moduli employed in Eq. [16] are given in Table V.

Fig. 11

Components of σ( R ) for the α phase calculated from the LSDF and Eq. [16] at a macroscopic stress value of 540 MPa, shown on slices normal to ND through the hexagonal Ω _fr . Recall that specimen directions, LD, TD, and ND correspond to x, y, and z, respectively. (a) σ _xx , (b) σ _yy , (c) σ _zz , (d) σ _yz , (e) σ _xz , and (f) σ _xy

Fig. 12

Components of σ( R ) for the β phase, calculated from the LSDF and Eq. [16] at a macroscopic stress value of 540 MPa, shown on slices normal to the ND through the cubic Ω _fr . (a) σ _xx , (b) σ _yy , (c) σ _zz , (d) σ _yz , (e) σ _xz , and (f) σ _xy

Table V Nonzero Components of the Elastic Stiffness Tensor for Each Phase Employed in the Determination of σ( R )*

5 Discussion

The stress distributions depicted in Figures 11 and 12 exhibit some interesting trends. The first indicator that significant variations exist is the 500 MPa range in the σ _xx component (LD) in each phase. The off-axis stresses, σ _yy and σ _zz , also vary by over 500 MPa and are both positive and negative. These results illustrate that the stress state at many orientations is not uniaxial tension. Finally, from the nonzero values of the shear components of stress, we see that the principal directions of the stress-state distributions do not necessarily align with the LD, TD, and ND. Armed with the full lattice-strain and crystal-stress tensors at every point in the orientation space, we can begin to address the crystal-level material response and identify worst-case orientations. Here, we examine these using the α-phase σ(R), to examine potentially hard and soft orientations.

5.1 Resolved Shear Stress

An extreme inelastic anisotropy creates a virtual inelastic inextensibility along the c axis in hcp materials such as α-titanium.[21] The most easily activated slip systems are the basal {0001} $\left\langle {11\bar 20} \right\rangle$ and prismatic $\left\{ {10\bar 10} \right\}$ $\left\langle {11\bar 20} \right\rangle$ families, neither of which accommodate extension of the c axis. There are pyramidal systems available in Ti-6Al-4V that accom.modate c + a slip; however, they are approximately 3 to 5 times harder to activate. Thus, a hard orientation results when relatively small values of shear stress, as compared to the critical value, are resolved on the basal and prism planes. The experiments were conducted on Ti-6Al-4V but hard orientations have been implicated in many fatigue or fracture-related failures in titanium alloys. A particularly deleterious condition known as dwell fatigue occurs in alloys such as Ti-6Al-2Sn-4Zr-2Mo.[22–25] Dwell fatigue results in significantly lower lives for loading situations containing a tensile hold component.[26] We seek to leverage σ( R ), to identify hard orientations in the α phase, which could potentially be used to identify failure-prone grains in an aggregate.

Determination of the resolved shear stresses on the basal {0001} $\left\langle {11\bar 20} \right\rangle$ and prismatic $\left\{ {10\bar 10} \right\}$ $\left\langle {11\bar 20} \right\rangle$ slip systems is extremely straightforward with σ( R ) in hand; the Schmid tensors can be applied to the components in the crystal frame associated with each orientation. To more clearly illustrate hard orientations in the loaded Ti-6Al-4V specimen, consider the orientation-dependent resolved shear stresses, $\tau _{{\text{rss}}}^i ({\textsf{R}})$, over the six most readily activated slip systems (three {0001} $\left\langle {11\bar 20} \right\rangle$ and three $\left\{ {10\bar 10} \right\}$ $\left\langle {11\bar 20} \right\rangle$). A useful scalar plot illustrating the availability of plastic deformation can be formulated as the maximum magnitude among the six at each orientation, normalized by the isotropic maximum resolved shear stress from the macrostress:

$$ \hat \tau _{{\text{rss}}} ({\textsf{R}}) = \frac{2} {{S_{xx} }}\mathop {\max }\limits_{i = 1}^6 \left| {\tau _{{\text{rss}}}^i ({\textsf{R}})} \right| $$

(17)

Note that $\hat \tau _{{\text{rss}}} ({\textsf{R}})$ is a function of both the crystal orientation and the fully three-dimensional stress state at every orientation. It serves to indicate orientations that, with respect to the loading, have at least one slip system supporting resolved shear stress, and that, as a result, are likely to yield. This field is shown over the orientation space in Figure 13. To further illustrate the effects of triaxial stresses on $\hat \tau _{{\text{rss}}} ({\textsf{R}})$, the same quantity was calculated from an isostress (Ruess) field, σ ^*( R ) = S ∀ R , which is shown in Figure 14(a). The differences, which arise from the nonuniform and triaxial nature of σ( R ), are salient. Figure 14(b) is included as a visualization aid, depicting the hcp unit cell orientations at key locations in orientation space. First, the zero values of resolved stress expected at the ±Y positions of the fundamental region (where the c axis is parallel to the loading axis) for a uniaxial stress state are not observed in Figure 13, but are present in Figure 14(a). One reason for this discrepancy can be attributed to the nonzero σ _yy magnitudes in σ( R ) at the same orientations (Figure 11(b)). Second, the reversal of maxima and minima on the midplane at the extreme ±X locations stems from the fact that the magnitudes of σ _xx in σ( R ) at these orientations are less than half the applied stress (S _xx  = 540 MPa); in fact, these are the minimum values of σ _xx ( R ). These differences in $\hat \tau _{{\text{rss}}} ({\textsf{R}})$ underscore the critical importance of capturing intergranular stress variations with σ( R ), for the purpose of identifying hard and soft orientations.

Fig. 13

Normalized maximum resolved shear stress, $\hat \tau _{{\text{rss}}}$, over the basal and prismatic slip systems in the Ti-6Al-4V aggregate (Eq. [17]). The applied macrostress was S _xx  = 540 MPa. A value of unity indicates the maximum shear stress for an isotropic medium subject to the same macrostress

Fig. 14

(a) The $\hat \tau _{{\text{rss}}}$, over the basal and prismatic slip systems from an isostress (Ruess) σ ^*( R ); i.e., σ ^*( R ) = S ∀ R . This contrasts with Figure 13 rather starkly, highlighting the varying triaxial nature of σ( R ) despite the uniaxial macrostress. (b) Schematic depicting the orientation of the hcp unit cell at key locations in the hexagonal fundamental region of Rodrigues space. Recall that X, Y, and Z correspond to specimen directions LD, TD, and ND, respectively

To understand how the resolved shear stress might be distributed within a polycrystalline aggregate, each orientation on the EBSD map shown in Figure 3 may be colored by $\hat \tau _{{\text{rss}}} ({\textsf{R}})$, as shown in Figure 15. Orientations with larger values of $\hat \tau _{{\text{rss}}}$ are more prone to yielding as the macroscopic stress increases. These orientations would be commonly denoted as crystallographically soft orientations, with respect to basal or prismatic slip. Grains that have these orientations will likely yield. Smaller values of $\hat \tau _{{\text{rss}}}$ (blue hues) indicate hard or yield-resistant orientations. While there will be local fluctuations in stress due to grain interactions, the orientation-averaged values of $\hat \tau _{{\text{rss}}}$ shown in Figure 15 could be employed as a preliminary search for potential hard (or soft) orientations in the microstructure. Dwell fatigue is hypothesized to occur in grains with very low values of $\hat \tau _{{\text{rss}}}$. Fracture instead of slip occurs in such grains, and fracture planes have been identified as being parallel or nearly parallel to the basal plane.[22–25] Much of this work, however, implicitly assumes a uniaxial stress state regardless of orientation in the classification of hard or soft (cf. Reference 27).

Fig. 15

Values of $\hat \tau _{{\text{rss}}}$( R ) for the α phase calculated from σ( R ) plotted on the orientations from the EBSD data shown in Figure 3. The source field is shown in Figure 15. Black regions correspond to β grains. The macroscopic stress level was 540 MPa, and unity indicates the maximum shear stress for an isotropic medium subject to the same macrostress

6 Summary and direction

A synchrotron X-ray diffraction method for measuring the orientation-averaged stress tensor in each phase of a loaded two-phase Ti-6Al-4V specimen was presented. The method consists of measuring lattice SPFs from a Ti-6Al-4V specimen deformed in situ within the experimental station. The lattice strains are converted to a lattice strain tensor field over orientation space using a method motivated by QTA, which we refer to as QSA. The stress distribution, σ( R ), was determined using Hooke’s law and the single-crystal elastic moduli for each phase. A precise geometric model of the experiment was constructed, to account for experimental artifacts that conspire to create large errors in the experimental data.

The stress distributions in each phase of the loaded Ti-6Al-4V sample, which were determined using the QSA analysis, exhibited significant variations in both magnitude and direction. Stress states within the aggregate varied significantly from the macroscopically applied stress. In each phase, fluctuations equal to the magnitude of the applied macroscopic stress (540 MPa) were apparent for all normal stress values, and 300 MPa fluctuations were observed in the shear components.

The utility of the σ(R) approach was demonstrated by calculating the resolved shear stress in the α phase on the basal plane, $\hat \tau _{{\text{rss}}}$, for each crystal orientation. Because the stress states were not uniformly uniaxial, the pattern over the orientation space contained some counterintuitive regions that differed starkly with an isostress counterpart. Maps of $\hat \tau _{{\text{rss}}}$ values for a polycrystalline aggregate illustrated the hard and soft regions of α microstructure.

6.1 Direction

The experiments and analysis of the two-phase Ti-6Al-4V data are presented in this article as an example of the variations in the stress state that exist under “simple” uniaxial loading. The resolved shear stress is presented as a simple micromechanical indicator of yielding in soft orientations or fracture in hard orientations. The map in Figure 15 demonstrates the variability in $\hat \tau _{{\text{rss}}}$ that can be present in a particular microstructure and graphically illustrates which orientations might be at risk under uniaxial loading. Certainly one could extend this analysis by proposing critical values of $\hat \tau _{{\text{rss}}}$ and possibly determining the volume fractions of the material that falls outside a particular “factor of safety.” Applying the knowledge gained from our experiments to an engineering component, in general, however, must involve a model. The stress distributions and parameter maps we have shown are specific to uniaxial loading. As soon as the macroscopic stress-state changes, the at-risk orientations will change. Interaction with crystal-scale modeling formulations, therefore, is perhaps the greatest utility of these data. As shown in recent work, stress distributions predicted using the QSA technique had excellent agreement with finite element results using polycrystal plasticity[10] for the loading of sintered copper in uniaxial tension. Using simulations, one can test situations that can never be replicated experimentally. In addition to imposing multiaxial macroscopic loading, the model is able to predict local variability that arises due to crystallographic neighborhood and grain-shape effects. One possibility includes using spatially resolved polycrystal plasticity modeling frameworks, such as those based on finite elements or discrete Fourier transform,[28,29] to equilibrate a microstructure, as shown in Figure 15. Orientations in a two- or three-dimensional microstructure could be seeded with stress values from σ( R ), and allowed to come to equilibrium via an elastoviscoplastic constitutive model. This type of synthesis between experiment and simulation could serve to approximate the effects of intergranular stresses, especially at phase boundaries, which could, in turn, illuminate new failure-prone regions. The stress data from the crystalline scale from the σ( R ) experiment, however, represent an important experimental yardstick for measuring the performance of multiscale modeling formulations; favorable comparisons between simulation and experiment build trust in both.