Introduction

Earthquake catalogs constitute a robust and beneficial tool for a variety of seismic analyses. Since seismicity is directly associated with physical quantities and mechanical properties of the crust such as strain accumulation, pore–fluid interactions and frictional response of the rupture zones, earthquakes provide a major source of information that cannot be usually obtained by direct measurements. Spatial and temporal seismicity rate anomalies are essentially reported as the most frequent intermediate-term precursory phenomenon in timescales varying from a few days to several years. The use of the well-established Gutenberg–Richter (G–R) law has been routinely incorporated into many seismic hazard assessment studies (e.g., Cornell 1968; Convertito et al. 2012). Alternatively, non-parametric approaches can be performed for hazard assessment evaluation under certain conditions (e.g., Kijko et al. 2001; Lasocki and Orlecka-Sikora 2008).

Seismic events may be controlled by either natural or anthropogenic factors. During the last decades, the rising demands for energy and minerals have sharpened the problem of hazards induced by exploration and exploitation of georesources (Davis et al. 2013). Among the diverse technologies capable of inducing earthquakes, one of the most well studied origins of anthropogenic hazard is underground mining. The undesirable rockmass response to mining operations was firstly observed back in the eighteenth century and during the last years it is being constantly reviewed and documented (e.g., Gibowicz and Lasocki 2001; Li et al. 2007; Gibowicz 2009, and references therein). A variety of factors control the rockmass fracturing and nucleation process in mines such as tectonic stresses accumulation, removal of material from the mine, explosions and the interaction among seismic events and rockbursts. The instability of mining activities, especially when they are extended, may result in the residual subsidence and localized or generalized collapsing, potentially with significant societal and economic impacts. There are numerous documented cases where mining-induced seismicity has caused personnel injuries, production losses, extensive damage to infrastructure, collapse of drifts and stopes, and occasionally, fatalities. For all these reasons, seismic hazard assessment in mines is a task of paramount importance.

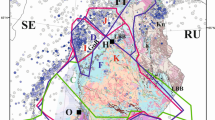
The purpose of this study is to evaluate seismic hazard parameters in connection with the evolution of mining operations and therefore to detect a causative relationship between seismic events and mining operations. The time-dependent hazard parameters to be estimated are the activity rate, the Gutenberg–Richter b-value, the mean return period and the exceedance probability of a prescribed magnitude for selected time windows related with the advance of the mining front. Four magnitude distribution estimation methods are applied and the results obtain from each one are compared with each other. Those approaches are maximum likelihood using the unbounded Gutenberg–Richter relation-based model (GRU), maximum likelihood using the upper-bounded Gutenberg–Richter relation-based model (GRT), unbounded non-parametric kernel estimation (NPU) and upper-bounded non-parametric kernel estimation (NPT). In addition, three different ways to construct subsequent datasets are applied: Time windows of constant duration, time windows with constant event number and time windows corresponding to constant front advance position. The spatial constraints are set in terms of the distance perpendicular and normal to the mining front at each time point (beginning and ending of time windows). The method is applied and results are discussed for the longwall mining of panel 3 in coal seam 503 in Bobrek colliery in Upper Silesia Coal Basin (USCB) in Poland, during 2009–2010. As shown in Fig. 1, this is a large area where coal mining has been carried out since the eighteenth century and continues till nowadays in more that thirty mines in which coal is exploited by applying the longwall method.

Fig. 1
figure 1

The location of the Bobrek mine in Upper Silesia Coal Basin, Poland. Figure comes from TCS-AH platform https://tcs.ah-epos.eu/

Full size image

Data

Bobrek Mine is a hard coal mine located in Bytom city in the area of USCB, Poland (Fig. 1). USCB constitutes one of the most seismically active mining areas worldwide, with almost 56,000 mining tremors of energy E > 105 J recorded between 1974 and 2005 (Stec 2007). The analysis of our study was based on selected set of data connected with exploitation in panel No. 3 in coal seam 503. This dataset is retrieved due to the specially organized virtual Laboratory for Monitoring Mining Induced Seismicity (LMMIS) where seismic data and technological data, such as mining front advance, were gathered. The seismic data had been prepared based on integration of two seismological networks operating at different scales (registration of events in the near and far seismic field). Additionally, information about the geology and the tectonics of the area was available. This set of data is integrated as an episode, which comprehensively describes a geophysical process induced or triggered by human technological activity, posing hazard for populations, infrastructure and the environment. All the data from this episode are available on TCS-AH platform as BOBREK MINE: local seismicity linked to longwall mining (https://tcs.ah-epos.eu/#episodes:BOBREK).

During underground mining works of longwall panel 3/503, a total of 2996 seismic events were recorded and analyzed, with a seismic energy greater than 102 J (local magnitude M L > 0.1), occurred from April 12th, 2009 until July 8th, 2010. The strongest observed events with local magnitudes equal to 2.9, 3.7, 3.0 and 2.8 (seismic energy greater than 107 J) took place on May 20th 2009, December 16th 2009, February 5th 2010 and March 3rd 2010, respectively (Table 1). Figure 2 shows the local magnitude histogram. The information about positions of the longwall excavation front advance in Bobrek mine is given as polygon coordinates in different time moments. The distance between subsequent positions of the mining front is approximately 50 m and time interval is one month. The foci of the seismic events caused by underground mining operations in panel No. 3, the locations of underground seismic stations and the position of the mining front advance during excavation of that longwall are demonstrated in Fig. 3 (figure is a snapshot of 3D visualization available via TCS-AH platform). The average seismic activity of the panel 3/503 was 6.6 events per day (Fig. 4). However, this rate is far from being considered as stable since there are significant seismic activity changes in time. In Fig. 4 it is shown that seismicity rates start growing from the beginning of November 2009. Then, the largest event occurred (M L = 3.7). The highest seismic activity equal to 18.4 events per day was observed from middle of January up to the middle of April 2010 and during that period two other strongest events occurred.

Table 1 Events with M L ≥ 2.8 which occurred in analyzed period of time
Full size table
Fig. 2
figure 2

Histogram of local magnitude of seismic events

Full size image
Fig. 3
figure 3

Distribution of seismic events during excavation of longwall panel no. 3 in Bobrek Mine. Black triangles represent the nearest seismic stations, and black lines show the subsequent positions of the longwall excavation front advance

Full size image
Fig. 4
figure 4

Seismic activity plot. Blue bars show the number of events per 2 weeks. Black line is cumulative number of events. Red lines represent the date of mining front localization

Full size image

Methodology

Four different magnitude distribution estimation methods are applied presented in the following sub-sections. Hazard parameters are calculated and plotted for each one of the time windows for which sufficient data are available in order to perform the necessary calculation. A different minimum number of events in each window is considered for the calculations to be performed, according to the method selected: for unbounded Gutenberg–Richter method it is 7; for upper-bounded Gutenberg–Richter method it is 15; and for non-parametric kernel-based methods it is 50 events.

Note that for the Unbounded models (GRU and NPU) an infinite upper magnitude limit, M max, is considered whereas in the Truncated (upper-bounded) approaches (GRT and NPT) M max is evaluated using the Kijko–Sellevoll generic formula (Kijko and Sellevoll 1989; Kijko 2004; Lasocki and Urban 2011). If convergence is not reached the Robson and Whitlock (1964) simplified formula is used: M max = 2M maxobs–M max2obs, where M maxobs and M max2obs stand for the largest and second largest magnitudes in a given catalog, respectively.

The hazard parameters evaluated in this study are the mean return period for a specified magnitude and the exceedance probability of a specified magnitude to be exceeded within a certain time period. The mean return period of magnitude M is the average elapsed time between the consecutive earthquakes of magnitude M. Given the mean activity rate for events with M ≥ M min, λ, in a specified time period and the corresponding cumulative magnitude distribution function, F(M), the mean return period is estimated as:

$$ T = \frac{1}{\lambda (1 - F(M))} $$
(1)

The exceedance probability of a specified magnitude, M, during a predefined time period, Δt, is given as

$$ P = 1 - e^{ - \lambda \Delta t(1 - F(M))} . $$
(2)

The cumulative magnitude distribution function, F(M), is calculated with respect to the selected method:

Unbounded GR law (GRU)

Assume that the unlimited Gutenberg–Richter relation leads to the exponential model of distribution for events with magnitude above the catalog completeness level M min. Under this assumption, an infinitely large maximum magnitude is possible. The shape parameter of this distribution and consequently the G–R b-value is estimated by maximum likelihood method (Aki 1965; Utsu 1999) with the Probability Density Function (PDF) of magnitudes given as:

$$ f(M) = \beta e^{{ - \beta \left( {M - M_{\hbox{min} } + \frac{\Delta M}{2}} \right)}} $$
(3)

with parameter β = ln10·b, where b stands for the well-known G–R b-value, which is estimated by the well-known Aki (1965) maximum likelihood estimator as:

$$ b = \frac{1}{{\ln (10)\left[ {\left\langle M \right\rangle - (M_{\hbox{min} } - \Delta {\rm M}/2)} \right]}}, $$
(4)

where \( \langle M\rangle \) is the sample mean of the considered events. The introduction of term ΔM/2 accounts for a correction for the finite binning width of the catalog, ΔM (Utsu 1966; Bender 1983), which is equal to the minimum non-zero difference among data. The corresponding Cumulative Distribution Function (CDF) of (3) is:

$$ F(M) = 1 - e^{{ - \beta \left( {M - M_{\hbox{min} } + \frac{\Delta M}{2}} \right)}} \quad {\text{for}}\quad M \ge M_{\hbox{min} } ,\quad 0\quad {\text{otherwise}} $$
(5)

Truncated GR law (GRT)

The assumption on the upper-bounded Gutenberg–Richter relation leads to the upper truncated exponential model of distribution for events with magnitude above the catalog completeness level M min. The PDF of magnitudes is given as (Page 1968; Kijko and Sellevoll 1989, also for b-value evaluation):

$$ F(M) = \frac{{\beta e^{{ - \beta \left( {M - M_{\hbox{min} } + \frac{\Delta M}{2}} \right)}} }}{{1 - e^{{ - \beta \left( {M_{\hbox{max} } - M_{\hbox{min} } + \frac{\Delta M}{2}} \right)}} }}\quad {\text{for}}\quad M_{\hbox{min} } \le M \le M_{\hbox{max} } ,\quad 0\quad {\text{otherwise}} $$
(6)

With β and ΔM/2 as explained in Eqs. (3) and (4). The corresponding CDF of (6) is:

$$ F(M) = 1\left\{ {\begin{array}{*{20}l} 0 \hfill & {\text{for}} \hfill & {M < M_{\hbox{min} } } \hfill \\ {\frac{{1 - e^{{ - \beta \left( {M - M_{\hbox{min} } + \frac{\Delta M}{2}} \right)}} }}{{1 - e^{{ - \beta \left( {M_{\hbox{max} } - M_{\hbox{min} } + \frac{\Delta M}{2}} \right)}} }}} \hfill & {\text{for}} \hfill & {M_{\hbox{min} } \le M \le M_{\hbox{max} } } \hfill \\ 1 \hfill & {\text{for}} \hfill & {M > M_{\hbox{max} } } \hfill \\ \end{array} } \right. $$
(7)

Non-parametric approaches (NPU and NPT)

The kernel estimator approach proposed by Kijko et al. (2001) is a non-parametric (model free or data driven) alternative for estimating the magnitude distribution functions. This non-parametric approach is based on the kernel density estimator that totals the symmetric probability densities (kernels), individually associated with data points as (Parzen 1962; Silverman 1986):

$$ \hat{f}(M|\{ M_{i} \} ,h) = \frac{1}{nh}\sum\limits_{i = 1}^{n} K \left( {\frac{{M - M_{i} }}{h}} \right) $$
(8)

where h is a non negative smoothing parameter (bandwidth), M i are the magnitudes and K(x) is a kernel function. The Kernel estimations chosen here for probability density (9) and cumulative distribution (10) have the forms of those adopted by Lasocki and Orlecka-Sikora (2008):

$$ \hat{f}_{M} (M) = \frac{{\sum\nolimits_{i = 1}^{n} {\frac{1}{{a_{i} h}}} e^{{ - \frac{1}{2}\left( {\frac{{M - M_{i} }}{{a_{i} h}}} \right)^{2} }} }}{{\left( {\sqrt {2\pi } } \right)\sum\nolimits_{i = 1}^{n} {\left[ {\varPhi \left( {\frac{{M_{\hbox{max} } - M_{i} }}{{a_{i} h}}} \right) - \varPhi \left( {\frac{{M_{\hbox{min} } - M_{i} }}{{a_{i} h}}} \right)} \right]} }} $$
(9)
$$ \hat{F}_{M} (M) = \frac{{\sum\nolimits_{i = 1}^{n} {\left[ {\varPhi \left( {\frac{{M - M_{i} }}{{a_{i} h}}} \right) - \varPhi \left( {\frac{{M_{\hbox{min} } - M_{i} }}{{a_{i} h}}} \right)} \right]} }}{{\sum\nolimits_{i = 1}^{n} {\left[ {\varPhi \left( {\frac{{M_{\hbox{max} } - M_{i} }}{{a_{i} h}}} \right) - \varPhi \left( {\frac{{M_{\hbox{min} } - M_{i} }}{{a_{i} h}}} \right)} \right]} }}, $$
(10)

where n is the sample size, Φ(x) is the standard Gaussian cumulative distribution, a i (i = 1,2, … n) are the local bandwidth factors and mi, are the magnitudes with M min ≤ M ≤ M max. Note that M min is equal to the completeness threshold of a given catalog. It is assumed that the magnitude distribution is unlimited from the right hand side (i.e., infinite maximum magnitude). The shape of the kernel estimates depends primarily on the value of h. From the point of view of the use of estimators (9), (10) in the hazard analysis, a global, integrant agreement between the actual density and its estimates is of the utmost importance. Therefore, we select the smoothing factor applying the least squares cross-validation technique that requires minimizing the integral of the squared difference between the actual density, f(ξ), and the estimate (e.g. Bowman et al. 1984):

$$ \hat{f}(\xi ) = \int\limits_{ - \infty }^{\infty } {\left[ {\hat{f}(\xi ) - f(\xi )} \right]^{2} } {\text{d}}\xi $$
(11)

It has been shown (Kijko et al. 2001) that in the case of the Gaussian kernel this criterion is fulfilled if h is the root of the equation:

$$ \sum\nolimits_{i,j} {\left\{ {\left[ {\frac{{(M_{i} - M_{j} )^{2} }}{{2h^{2} }} - 1} \right]\exp \left[ { - \frac{{(M_{i} - M_{j} )^{2} }}{{4h^{2} }}} \right] - 2\left[ {\frac{{(M_{i} - M_{j} )^{2} }}{{h^{2} }} - 1} \right]\exp \left[ { - \frac{{(M_{i} - M_{j} )^{2} }}{{2h^{2} }}} \right]} \right\}} = 2n $$
(12)

The local bandwidth factors, {α i } can modify the width of the kernels at certain data points. Due to the fact, that the most important for the hazard analysis range of magnitudes, is that of the larger values, where the data are very sparse, the present version of the estimators uses the bandwidth factors that widen the kernels associated with data points from this range (Lasocki and Orlecka-Sikora 2008):

$$ a_{1} = \frac{1}{{\left[ {\frac{{\hat{f}(M_{i} |\{ M_{i} \} ,h}}{g}} \right]^{1/2} }}, $$
(13)

where \( \hat{f} \), is the constant kernel estimator in the unbounded magnitude range, and

$$ g = \left[ {\prod\nolimits_{i = 1}^{n} {\hat{f}(M_{i} |\{ M_{i} \} ,h)} } \right]^{1/n} $$
(14)

is the geometric mean of all constant kernel estimates (Silverman 1986).

Parameter values defined

Mining tremors occurrence is strongly associated with the excavation operations and therefore, seismicity properties and hazard parameters are estimated as a function of time and front advance. For this purpose, only the fraction of events which satisfies predefined properties is considered for such calculations. These events are selected after applying the following constrains: The completeness magnitude of the catalog was identified by considering the stations distances from the focal areas and the signal to noise ratio (Mutke et al. 2016). In such way M min was set equal to 0.6. The margin along front strike (equal for both directions of the front strike) and distance along the front advance (equal for both in front of and behind the front) was set equal to 50 and 100 m, respectively, following Kozłowska (2013). Calculations were performed for overlapping time windows generated in three different modes: According the “time mode”, events included in subsequent 30-day time windows were considered, overlapping per 1 day. In this approach time windows of the same span are used for hazard parameter evolution estimation. In the “events mode”, the time windows are selected in such a way that they include equal number of events (also overlapping per one day) and therefore the parameter estimation errors are comparable in all the datasets. Finally, in the “front mode”, a subsequent time window starts at the time point when the front advance is moved from the position it was in the beginning of the previous time window, to a distance indicated by a predefined value. In this case, the time windows correspond to approximately equal material mass removal from the mine (those windows are also overlapping per 1 day). The parameters set for our analysis in those three modes were 30 days in the “time mode”, 80 events in the “event mode” and 50 meters in the “front mode”. Finally, the event magnitude for the mean return period and the exceedance probability evaluation was set to 3.0, equal to the second largest magnitude in the dataset.

Results

We analyzed changes of seismic activity rate, b-value, return period of M L = 3.0 and exceedance probability of M L = 3.0 (within 30 days) as a function of time before the occurrence of strong events with M L ≥ 2.8 (Figs. 5, 6, 7). Four events with such magnitudes occurred in analyzed period of time (Table 1). In further analyses, we considered only events with IDs 2–4, because of the too short time period between the initiation of registrations and occurrence of the event with ID 1.

Fig. 5
figure 5

Changes of seismic activity rate (a) and b-value (b) in time calculated using: time windows of 30 days, event windows of 80 events, front windows of 50 m (see text for details). Strong events are plotted with gray dashed vertical lines. Gray horizontal lines indicate time periods chosen to calculate mean values of parameters (indicated by the numbers in colored fonts)

Full size image
Fig. 6
figure 6

Exceedance probability of M L = 3 calculated using: time windows of 30 days (a), event windows of 80 events (b), front windows of 50 m (c)

Full size image
Fig. 7
figure 7

Return period of M L = 3 calculated using: time windows of 30 days (a), event windows of 80 events (b), front windows of 50 m (c)

Full size image

It can be observed that in the case of events (2) and (3) activity rate increases, although in different manner, before the occurrence of considered events (Fig. 5a). The opposite statement can be done for event (4), where for both time and front windows activity rate decreases before the event. However, slight increase shortly before the event is observable in the case of event window mode which due to the constant amount of events in each window is more sensitive in detecting sudden changes in occurrence rates. Additionally, it is worth mentioning that only the curve resulting from event windows shows a evident peak in activity rate before event (3). In the case of other windows the increase is slight.

Changes in b-values before the occurrence of strong events are also not completely consistent with each other. Before events (2) and (4) decrease of b-value can be observed. However, before the occurrence of event (3), b-value increases in the case of all window types. Again, changes in the case of curve obtained using event window mode are the largest (Fig. 5b).

To describe quantitatively how distribution of hazard parameters changes before high magnitude events, we compared the last value of given parameter calculated before the occurrence of the event with the mean value of the same parameter calculated in time window from the beginning of observations to 14 days before considered event (Fig. 5). The time period of 14 days was chosen on the basis of observations of parameter changes before the big events (Fig. 5). The results reveal that seismic activity rate ratio is >1 for all events and window types, with a maximum value of 13.23 for event window for event (3) (Fig. 8a). b-value ratios of events (2) and (4) have generally values <1, what is a result of b-value decrease before big events mentioned earlier, however, for the event (3) the ratio of b-values are highly above 1 (Fig. 8b).

Fig. 8
figure 8

Ratios of the last values of activity rate (a) and b-value (b) before events (2), (3) and (4) to the mean values of these parameters calculated in time periods marked in Fig. 5. Black solid lines indicate ratio value equal 1

Full size image

The values of exceedance probability of ML = 3.0 (within 30 days) and return period of ML = 3.0 just before the occurrence of events (2), (3) and (4) are plotted in Fig. 9. It can be observed that exceedance probability values obtained using Gutenberg–Richter methods are much higher than those estimated with non-parametric kernel methods (Fig. 9). Only event windows used in kernel methods give significantly high probabilities in case of events (3) and (4). Additionally, the increase of exceedance probability calculated with kernel methods occurs just before high magnitude events (Fig. 6), which makes it difficult to use for prediction purposes. On the contrary, changes of exceedance probability obtained using Gutenberg–Richter approaches are much more gradual, and thereby it is easier to follow the observed trend.

Fig. 9
figure 9

Exceedance probability values before events (2), (3) and (4) calculated with unbounded Gutenberg–Richter (a), upper-bounded Gutenberg–Richter (b), unbounded kernel (c) and upper-bounded kernel (d) methods. Black solid lines indicate exceedance probability equal 0.5

Full size image

Return periods of M L = 3.0 calculated with non-parametric kernel methods are comparable to those calculated with Gutenberg–Richter methods only in case of event (3) (Fig. 10). In all other cases, the values of kernel estimations of return periods are much higher. It is worth mentioning that in the case of event (3), kernel-based return periods for event windows are even lower than Gutenberg–Richter ones. In case of event (4), the lowest kernel return periods are also calculated on the basis of event windows (Fig. 10). These and previous observations can lead us to a conclusion that non-parametric kernel-based methods give compatible hazard results only if event window is used for calculations (i.e., meaning constant number of events in variable size window).

Fig. 10
figure 10

Return period values before events (2), (3) and (4) calculated with unbounded Gutenberg–Richter (a), upper-bounded Gutenberg–Richter (b), unbounded kernel (c) and upper-bounded kernel (d) methods. Black solid lines indicate return period equal 10

Full size image

Previous analysis (Fig. 8, 9, 10) of parameters’ changes before events (2), (3) and (4) leads us to the following conclusions concerning expectance of events on the basis of time-dependent hazard calculations. First, on the basis of temporal changes of activity rate, b-value, exceedance probability and return period, event (4) can be considered as the most expected one (activity rate increase, b-value decrease, high exceedance probability according to all methods, relatively short return period). Second, estimations of exceedance probability and return period with kernel-based methods do not give any possibility to predict the event (2) despite the fact that activity rate and b-value changes can suggest the occurrence of an impending strong event.

Discussion and conclusions

The use of fundamental observational and empirical parameters such as activity rate and G–R b-value may prove to be helpful in evaluation of seismic hazard for specific study areas such as longwall mining. The G–R b-value has a clear physical interpretation, defining the relative proportion of the number of large events to small events. Anomalies in seismicity rates and b-value can be considered as an indicator of the stress state in rock mass (e.g., low b-values may indicate growing of stress, Scholz 1968). These anomalies are capable to lead to strong tremors and thus provide high seismic risk. Information of such kind can, therefore, be a premise for the decision to use specific measures to prevent bumps and adjust mining operations. Probability of the strong events occurring is higher when b-value is decreasing and simultaneously activity rate is increasing. In the present study, this case is clearly observed for events 2 and 4 for all window types (with the exception of b-value for event 2, which slightly increases when time window is considered). However, the activity rate is increased in all cases studied (Fig. 8a).

The need of introducing a non-parametric estimation for magnitude distribution arose from observed deviations of specific catalogs from G–R law in both natural and induced seismicity. Especially, induced seismicity exhibits diverse seismogenic processes in comparison with natural seismicity and it strongly depends on the human technological and production activities (Kijko et al. 1987; Trifu et al. 1993; Fritschen 2010; Maghsoudi et al. 2014). Two causes had been considered responsible for inconsistency of G–R law with the observed events distribution. The coupling between tectonic stresses and mining activities in Bobrek mine has been studied by Marcak and Mutke (2013). Specifically for event 2, Kozłowska et al. (2016) showed that it was a tectonic event triggered by the ongoing exploitation and that the subsequent seismicity was a result of combined tectonic, coseismic and mining-induced stresses.

First, this inconsistency was attributed to the presence of broadly defined types of mining events (e.g., Gibowicz and Kijko 1994): events directly related to the mining operations and events resulting from the release of residual tectonic stresses accumulated in the rock mass. These two types of events are characterized by extensively different properties and features. Second, the non-linearity was attributed to the local geology and tectonics, i.e., heterogeneity and discontinuity of the rock structures with different thickness, strength, different in various parameters. For example, Naoi et al. (2014) showed that the distribution of magnitudes is consistent with the G–R relationship only when events closely linked to blasting are not taken into account.

As a result, magnitude distribution complexity may arise, characterized by number of modes or bumps in magnitude density. Evidences for the existence of multimodal earthquake size distribution were presented in many papers (e.g., Gibowicz and Kijko 1994; Gibowicz and Lasocki 2001; Lasocki and Orlecka-Sikora 2008). Magnitude distribution may statistically significantly differ from the exponential distribution but the differences may be small (Urban et al. 2016). G–R model seems often inadequate to describe the earthquake size distribution.

To evaluate which estimation method would be more appropriate in our dataset, we performed statistical tests to examine the compatibility of earthquake size distribution with exponential distribution. First, we used Kolmogorov–Smirnov (K–S) goodness-of-fit one-sample test to check whether earthquake size distribution statistically differs from the exponential distribution. Details of this procedure and the corresponding findings in several cases of induced seismicity are described in the paper of Urban et al. (2016). Second, we examined the earthquake size distribution for its complexity using smoothed bootstrap test for multimodality. Multimodality test allows us to examine the presence of irregularities in the distribution of given magnitude values by demonstrating the presence of more than one mode or more than one bump in the probability density function (Lasocki and Papadimitriou 2006; Lasocki and Orlecka-Sikora 2008). These features indicate the presence and mixing of different processes generating the events.

To perform the multimodality and K–S tests, first the randomization of any observed magnitude has been done within the rounding error. Randomization of magnitude was carried out by transformation (Lasocki 2001; Lasocki and Papadimitriou 2006)

$$ \hat{M} \, = F^{ - 1} \, \{ u[F(M + 0.5\delta M) - F(M - 0.5\delta M)] + F(M - 0.5\delta M)\} , $$
(15)

where \( \hat{M} \) and M are randomized and observed magnitude values, respectively, Δ is accuracy of magnitude estimation, u is the value from uniform distribution [0, 1], F(·) is magnitude CDF, and F −1(·) is its inverse function.

In the K–S test case, we test the null hypothesis H 0: the distribution of magnitude is exponential. To verify H 0, we estimate p values and compare them with the adopted significance level α = 0.05. A small p value suggests that the null hypothesis may be false. In the test for multimodality case, we test two null hypotheses: H 10 : density function of earthquake size distribution has no more when 1 mode; H 20 : density function of earthquake size distribution has no more than 1 bump. Due to the fact that the magnitude randomization gives slightly different p-values and significances of the considered null hypotheses, we assumed as a final value its mean value (from 1000 magnitude randomized catalogs) considering their standard deviation as well.

The results from K to S test strongly suggest that earthquake size distribution is not exponential with mean p equal to 4.6 × 10−7 and standard deviation equal 3.9 × 10−7. Because we estimate G–R b-value from the sample it requires calculation of additional statistics (D m) (Urban et al. 2016). The value of the (D m) is 2.82 which confirms previous results with the significance at least equal to 0.01.

The mean significance of considered null hypotheses from test for multimodality is 0.11 for H 10 with standard deviation equal 0.02 and 0.04 for H 20 with standard deviation equal 0.02. The results indicated that with 89–96% probability magnitude distribution is more complex than linear model.

Based on the results of K–S test and smoothed bootstrap test for multimodality, the non-parametric method for estimate of hazard parameters would be more appropriate. On the other hand, non-parametric technique starts to be effective for sample sizes starting from 200 events (Kijko et al. 2001). However, the hazard analysis performed in the present study considers time windows which contain diverse and mainly smaller number of events. Taking into account the size of the dataset we may conclude that segmentally, the G–R model is a good approximation for this type of analysis, providing also more comprehensive and stable results.

As a summary, we conclude to the following points:

  • The obtained results strongly depend on the data number contained in the analyzed windows. According to that, event window approach may be preferable because it leads to identical or at least comparable uncertainties of the estimated parameters (equal size data samples are tested—see “Appendix A”).

  • Unbounded and upper-bounded GR approaches lead to similar results (see also “Appendix A”). In the same way, unbounded and upper-bounded non-parametric methods also lead to similar results. On the other hand, there are distinct differences between parametric and non-parametric estimation techniques.

  • Kernel-based methods exhibit sharp fluctuations of estimated parameter values, which are essentially, not practical in terms of prediction implications for datasets of such size. However, they seem to provide consistent results when event windows are considered.

  • On the basis of all methods’ results, the last event (4) can be considered as the most expected one. It should be noted that there are several other windows for which exceedance probability is practically 1, when the G–R approaches are considered.

  • The analysis of the catalog as a whole strongly indicates that earthquake size distribution does not obey G–R relation. However, smaller datasets in the analyzed windows show that G–R relation is an adequate approximation providing more stable results.