A Mathematical Modeling Study: Assessing Impact of Mismatch Between Influenza Vaccine Strains and Circulating Strains in Hajj

Abstract

The influenza virus causes severe respiratory illnesses and deaths worldwide every year. It spreads quickly in an overcrowded area like the annual Hajj pilgrimage in Saudi Arabia. Vaccination is the primary strategy for protection against influenza. Due to the occurrence of antigenic shift and drift of the influenza virus, a mismatch between vaccine strains and circulating strains of influenza may occur. The objective of this study is to assess the impact of mismatch between vaccine strains and circulating strains during Hajj, which brings together individuals from all over the globe. To this end, we develop deterministic mathematical models of influenza with different populations and strains from the northern and southern hemispheres. Our results show that the existence and duration of an influenza outbreak during Hajj depend on vaccine efficacy. In this concern, we discuss four scenarios: vaccine strains for both groups match/mismatch circulating strains, and vaccine strains match their target strains and mismatch the other strains. Further, there is a scenario where a novel pandemic strain arises. Our results show that as long as the influenza vaccines match their target strains, there will be no outbreak of strain H1N1 and only a small outbreak of strain H3N2. Mismatching for non-target strains causes about 10,000 new H3N2 cases, and mismatching for both strains causes about 2,000 more new H1N1 cases and 6,000 additional H3N2 cases during Hajj. Complete mismatch in a pandemic scenario may infect over 342,000 additional pilgrims (13.75%) and cause more cases in their home countries.

1 Introduction

Influenza viruses circulating worldwide cause respiratory tract infection known as seasonal influenza. In general, there are four types of influenza viruses: types A, B, C, and D. Usually, influenza infections are caused by influenza A and B viruses. Seasonal influenza presently infects one of each six people every year, with 3 to 5 million severe illness, and 290,000 to 650,000 respiratory deaths worldwide. Influenza viruses can be spread by airborne respiratory droplets (cough or sneeze), skin-to-skin contact (handshakes or hug), saliva (kissing or shared drinks), or by touching a tainted surface (blanket or doorknob). Seasonal influenza spreads readily in overcrowded areas like mass gatherings (World Health Organization 2018).

For more than a half century, vaccination has been the primary strategy for protecting and controlling influenza (Davenport 1962; Fiore et al. 2010), and influenza vaccines continue to decrease the impact of infection (Osterholm et al. 2012). However, individuals are repeatedly infected by seasonal influenza due to two types of antigenic variation: antigenic drift and antigenic shift. These variations make people susceptible to new subtypes that are genetically different enough from the old ones, regardless of prior infection by other influenza subtypes. In other words, if the new strains of influenza are genetically different enough from the old strains, people will be susceptible to them. If the genetic distance between the new strain and old strain is not very big, then people will have partial immunity (Couch and Kasel 1983; Sonoguchi et al. 1985; Ferguson et al. 2003). Hence, the influenza vaccine is updated yearly based on the most common strains circulating from the previous season, in order to match with new circulating strains that are predicted to cause infections (Cox and Subbarao 1999). WHO monitors influenza worldwide and recommends vaccine compositions twice each year for the northern and southern hemisphere influenza seasons.

Mismatching or poor matching is defined to be the case if the strains that are included in the vaccine are antigenically different from the circulating strains. The mismatch between the vaccine strains and circulating strains may take place when a drifted virus emerges after vaccine strains have been selected or a novel pandemic strain has spread (World Health Organization 2018). Vaccine effectiveness (VE) primarily varies depending on matching or mismatching between influenza vaccine strains and the circulating strains (Osterholm et al. 2012). A systematic review shows that the VE was 77% (95% confidence interval (CI) 67% to 86%) for the live attenuated influenza vaccine (LAIV) and 65% (95% CI 57% to 72%) for the trivalent inactivated vaccine (TIV) when the vaccine strains and circulating strains are matched. Furthermore, when the vaccine strains and circulating strains are mismatched, VE was 60% (95% CI 44% to 71%) for LAIV and 56% (95% CI 43% to 66%) for (TIV) (Tricco et al. 2013). These findings prove that there is cross-protection even when vaccine strains do not match circulating strains. Kelly et al. demonstrated that the seasonal vaccine has no protection against a pandemic influenza strain in any age group (Kelly and Grant 2009). Vaccine failure or low efficacy refers to poor matching between vaccine strains and circulating strains (Demicheli et al. 2018; Jefferson et al. 2010). Matching and mismatching, in actuality, is not binary, i.e., vaccination is not a perfect match or a perfect mismatch with the circulating strains.

Co-infection, i.e., infection by more than one strain of influenza, also known as concurrent infection, has been detected in seasonal influenza in different parts of the world (e.g., Sonoguchi et al. 1985, 1986; Shimada et al. 2006; Toda et al. 2006; Falchi et al. 2008; Ghedin et al. 2009; Lee et al. 2010; Liwen et al. 2010; Peacey et al. 2010; Calistri et al. 2011; Liu et al. 2011; Myers et al. 2011; Almajhdi and Ali 2013; Zhu et al. 2013; Tramuto et al. 2014; Jun Li et al. 2014; Zhang et al. 2015; Perez-Garcia et al. 2016; Pando et al. 2017; Gregianini et al. 2019). Individuals can be either infected by both strains at the same time (Liu et al. 2010) or infected by one strain and then infected by the other before recovery from the first strain. The phenomenon of co-infection is different from re-infection, where an individual who has been infected by one strain and then recovered is then infected by another strain, usually called a secondary infection.

Every year about three million Muslims perform Hajj to Makkah, Saudi Arabia. The Hajj is an annual Muslim pilgrimage and a mandatory religious obligation for all Muslims who are physically and financially capable of the commitment, the travel, and support of their family during their absence. This obligation is only mandatory once in a lifetime. The Hajj occurs during the last month (12th) of the Islamic calendar, and the Hajj ritual is held within six specific days during the month. Some pilgrims come only for the Hajj ritual, while others prefer to stay sometime before or after performing Hajj. At these times, pilgrims are in such close contact that transmission of respiratory tract infection is extremely high because of immense overcrowding.

The Hajj is epidemiologically significant because it brings together large numbers of people from all over the world who may be carrying different strains of influenza that other people may not be vaccinated against. Vaccination against influenza is recommended for all pilgrims by the Saudi Ministry of Health (Saudi Ministry of Health. Hajj and Umrah Health Regulations 2020). A proportion of those people may come to the Hajj, while they are vaccinated against their home influenza circulating strains, which are often different than strains circulating during Hajj. A detailed analysis at the Hajj covering the period between 2003 and 2015 demonstrated that mismatching between strains that included in the vaccine and the circulating strains is frequent (Alfelali et al. 2016). Different vaccines are made available for the northern and southern hemispheres due to significant differences between strains circulating in the northern and southern hemispheres. In this regard, Hajj is similar to events like the Olympics and World Cup, but it is unique in its extremely high population density, which generates homogeneous mixing in an extraordinarily large population.

Many mathematical studies have been done to better understand the dynamics of influenza transmission in one host population (since influenza is an air-borne disease) and multi-strains of influenza with varying levels of cross-immunity (Castillo-Chavez et al. 1989; Gupta et al. 1996; Andreasen et al. 1997; Gupta et al. 1998; Lin et al. 1999; Gog and Swinton 2002; Gog and Grenfell 2002; Kamo and Sasaki 2002; Lin et al. 2003; Boni et al. 2004; Restif and Grenfell 2005; Nuno et al. 2005; Adams and Sasaki 2007; Minayev and Ferguson 2008; Chamchod and Britton 2012; Chung and Lui 2016). Some influenza mathematical models have studied the dynamics of infection with two different populations and one strain of influenza (Iwami et al. 2007; Derouich and Boutayeb 2008). Evaluating the role of cross-immunity and determining the condition(s) for co-existence have been concentrated, overall, on these studies. Nune et al. demonstrated that host isolation and cross-immunity may stimulate sustained periodic oscillations (Nuno et al. 2005). Bremermann and Thieme manifest the occurrence of competitive exclusion, where one strain with the largest reproduction number persists and excludes the other strains (Bremermann and Thieme 1989). The reproduction number of the 1918–1919 influenza pandemic and other seasonal strains of influenza have been estimated to be in the range between 1.5 and 5.4 (Chamchod and Britton 2012). To the best of our knowledge, there is no mathematical model that incorporates both: two different populations, with the possibility that a proportion of each population is vaccinated, and two different strains of influenza. Any vector-borne disease (VBD) models, however, naturally involve two different populations (host and vector) that interact among each other. Some VBD models have considered two populations and two strains (Kribs-Zaleta and Mubayi 2012; Pelosse and Kribs-Zaleta 2012; Kribs-Zaleta 2014), or two diseases (Isea and Lonngren 2016; Okuneye et al. 2017).

The focus of our study is to assess the impact of matching and mismatching between vaccine strains and circulating strains during the Hajj, in a scenario where pilgrims from the northern and southern hemispheres carry genetically different strains of infection. A new deterministic model will be built to attain this goal.

2 Model Development

Because of the complexity of the model, we build up to it by adapting a basic SEIR model with vaccination to first two strains and then two populations.

2.1 Simple SEIR Model with Vaccination (One Population, One or Two Strains)

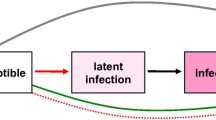
We begin with a simple SEIR model with vaccination, see Fig. 1, to explain the underlying assumptions and why we have different versions of it in the full model. In brief, the population is classified into susceptible, vaccinated, exposed, infected, and recovered classes (S, V, E, I, R). Susceptible and vaccinated individuals can be infected through their contact with infected individuals in class I, with a reduced rate for vaccinated individuals due to the vaccine’s protection. Infected individuals are moving to exposed class, E, and remaining noninfectious for an incubation period. Individuals in class E are moving to the infected class, I, and becoming infectious after the incubation period. Lastly, individuals in class I are moving to recovered class, R, after recovery. For the simple model (Fig. 1), there is only one class for each stage of the course of the infection. The simple model can be applied to an influenza disease model that considers one population and one strain.

Fig. 1

Simple SEIR with vaccination

In order to include two different strains of influenza, multiple copies of the simple model are required. Since the model describes a single mixing population with only one type of vaccine, there remain only one $S_i$ class and one $V_i$ class. However, those vaccinated individuals infected by one strain retain partial protection against the other strain, requiring a separate chain of exposed ($F_{ij}$), infective ($K_{ij}$), and recovered ($W_{ij}$) compartments for each strain. Thus vaccination history remains important until not the first exposure (as in the one-strain model), but the second. Initial infection of the $S_i$ or $V_i$ population with strain 1 or 2 therefore leads to four SEIR chains, as in Fig. 2. Although we are only considering one mixing population at this stage, we introduce the notation that will be used in the final model: each compartment’s first subscript i designates the population (1 or 2) to which it belongs, while a second subscript j indicates the strain (1 or 2) with which it has been infected.

To add the co-exposed classes and complete the model, each of the six pairs ($E_{1j}$, $F_{1j}$), ($I_{1j}$, $K_{1j}$), ($R_{1j}$, $W_{1j}$), $j=1,2$, in Fig. 2, will serve in the full model as the starting points (corresponding to (S, V)) of an SEIR cycle. Since co-infection is incorporated, there are classes exposed, $E_{13}$, infected, $I_{13}$, and recovered, $R_{13}$, from both strains. Plus, there are classes exposed by one strain and infected, $L_{1j}$, or recovered, $G_{1j}$ by the other strain and classes for infected by a strain and recovered from the other strain, $J_{1j}$ and $j=1,2$, see Fig. 3 when i=1 only.

Fig. 2

Single-infection SEIR chains for one population (i) and two strains (1, 2), starting from susceptible or vaccinated

Fig. 3

Compartmental diagram of the model for group i, $i=1,2$. The diagram without dotted arrows represents case one model, and the dotted arrows indicate incoming infected pilgrims in cases two and three. Group 1 imports infections of strain one only (green arrows), while group 2 imports strain two only (red arrows)

2.2 Full Model (Two Populations, Two Strains)

We divide the population who attend Hajj into two groups: pilgrims from the northern hemisphere, $i=1$, and pilgrims from the southern hemisphere, $i=2$, based on their influenza vaccine strains. Each group is categorized into 23 compartments according to vaccination and infection status for both strains, with total population for each group denoted by $N_i$ and the total population denoted by N. We define $n_i$ as the proportion of the total population occupied by each group. Again, a compartment’s first subscript indicates population or hemisphere of origin, $i=1$ or 2, and any second subscript denotes the strain of most recent infection, $j=1$ or 2 (3 for co-infection). A complete list of the state variables used in this model is shown in Table 1. A flowchart for the complete model would include two copies of Fig. 3—one for each population of origin—coupled only by the infection rates, which sum over all compartments infected with a given strain in both populations.

Since we examine transmission during the short timeline of Hajj, we do not include birth and death rates. The infection rate of susceptible individuals through their contacts with infectives in the model is standard incidence since the contact rate in Hajj is saturated, due to the large numbers of pilgrims. Furthermore, during the entire model, we assume nearly all of the pilgrims’ contact time is with other pilgrims. Thus, we are restricting our attention only to infections among pilgrims. We use multiple infection rates, $\beta _{mnj}$, for each combination of infecting group, receiving group, and strain types. The infection rates, $\beta _{mnj}$, are defined as the rate of infectious contacts from individuals in a group m to individuals in a group n multiplied by the probability of transmission of a strain j per contact. Susceptibles from both groups are at risk of getting infected by either strain. Each group has a proportion of individuals who have received the vaccine for their region $\phi _{i}\in (0,1)$. Vaccinated individuals can be infected at a reduced rate based on the matching/mismatching measures, $q_{ij}$. We assume that an individual can be co-infected from both strains; to get that, he/she must first be infected by one strain and then infected by the other. An individual will get permanent immunity from one strain after recovery, but he/she will still be susceptible to the other strain. For an individual to be permanently immunized from both strains, he/she must be infected by both strains, either co-infected or one after another, and then recover from both of them. For each strain, we assume there is a different recovery rate $\gamma _j$. We incorporate the idea of vaccine matching as a parameter, $q_{ij}$, that can tune between 0 and 1. If $q_{ij}=1$, that means there is a complete mismatch, between vaccine strain i and circulating strain j, and no protection at all. If $q_{ij}=0$, it is a perfect match between vaccine strain i and circulating strain j. In reality, it is going to be somewhere in between. A list of all parameters used in the model is shown in Table 2.

Table 1 Model variables with definition

Table 2 Parameter definitions and units

We will consider three versions of this model. The first case, where individuals do not arrive or leave (no recruitment or departure rates), is considered for the specific six days of the Hajj ritual. Case two, where individuals arrive and depart at constant rates, is a more complex approximation to Hajj pilgrims’ population dynamics. Case three, where individuals arrive before the six days of Hajj rituals and leave after these six days, mirrors the actual timeline at Hajj. In case three, there are three time periods. The first period, the arrival phase, is when pilgrims arrive gradually, the 38 days before the Hajj worship. The second period, the worship stage, is the actual intense six days of the Hajj ritual. The third period, the departure stage, is when pilgrims leave, 27 days after the Hajj ritual. Thus, we consider an approximate time frame of 90 days for the model.

2.3 Model Equations

A flowchart of the three cases of this model is illustrated in Fig. 3. The solid arrows only represent the case one model. The solid and dotted arrows represent cases two and three. The system of equations for case one model is given by system (1), when $\Lambda _i=\mu =0$ and for cases two and three by system (1), when $\Lambda _i$ and $\mu \ne 0$.

$$\begin{aligned} \frac{dS_{i}}{dt}= & {} (1- p_i)(1-\phi _i)\Lambda _{i} - d_{i1}S_{i} - d_{i2}S_{i} - \mu S_{i}\nonumber \\ \frac{dE_{i1}}{dt}= & {} {\frac{p_i}{2}(1-\phi _i)\Lambda _{i}} + d_{i1}S_{i} - d_{i2}E_{i1} - \eta _{1}E_{i1} - \mu E_{i1}\nonumber \\ \frac{dE_{i2}}{dt}= & {} {\frac{p_i}{2}(1-\phi _i)\Lambda _{i}} + d_{i2}S_{i} - d_{i1}E_{i2} - \eta _{2}E_{i2} - \mu E_{i2}\nonumber \\ \frac{dV_{i}}{dt}= & {} (1- p_i)\phi _i\Lambda _{i} - q_{i1}d_{i1}V_{i} - q_{i2}d_{i2}V_{i} - \mu V_{i}\nonumber \\ \frac{dF_{i1}}{dt}= & {} {\frac{p_i}{2}\phi _i\Lambda _{i}} + q_{i1}d_{i1}V_{i} - q_{i2}d_{i2}F_{i1} - \eta _1F_{i1} - \mu F_{i1}\nonumber \\ \frac{dF_{i2}}{dt}= & {} {\frac{p_i}{2}\phi _i\Lambda _{i}} + q_{i2}d_{i2}V_{i} - q_{i1}d_{i1}F_{i2} - \eta _2F_{i2} - \mu F_{i2}\nonumber \\ \frac{dE_{i3}}{dt}= & {} d_{i1}E_{i2} + d_{i2}E_{i1} + q_{i1}d_{i1}F_{i2} + q_{i2}d_{i2}F_{i1} -(\eta _1+\eta _2)E_{i3} - \mu E_{i3}\nonumber \\ \frac{dI_{i1}}{dt}= & {} {\frac{p_i}{2}(1-\phi _i)\Lambda _{i}} + \eta _1E_{i1} - d_{i2}I_{i1} - \gamma _1I_{i1} - \mu I_{i1}\nonumber \\ \frac{dI_{i2}}{dt}= & {} {\frac{p_i}{2}(1-\phi _i)\Lambda _{i}} + \eta _1E_{i2} - d_{i1}I_{i2} - \gamma _2I_{i2} - \mu I_{i2}\nonumber \\ \frac{dK_{i1}}{dt}= & {} {\frac{p_i}{2}\phi _i\Lambda _{i}} + \eta _1F_{i1} - q_{i2}d_{i2}K_{i1} - \gamma _1K_{i1} - \mu K_{i1}\nonumber \\ \frac{dK_{i2}}{dt}= & {} {\frac{p_i}{2}\phi _i\Lambda _{i}} + \eta _2F_{i2} - q_{i1}d_{i1}K_{i2} - \gamma _2K_{i2} - \mu K_{i2}\nonumber \\ \frac{dL_{i1}}{dt}= & {} \eta _1E_{i3} + d_{i2}I_{i1} + q_{i2}d_{i2}K_{i1} - \gamma _1L_{i1} - \eta _2L_{i1} - \mu L_{i1}\nonumber \\ \frac{dL_{i2}}{dt}= & {} \eta _2E_{i3} + d_{i1}I_{i2} + q_{i1}d_{i1}K_{i2} - \gamma _2L_{i2} - \eta _1L_{i2} - \mu L_{i2}\nonumber \\ \frac{dI_{i3}}{dt}= & {} \eta _1L_{i2} + \eta _2L_{i1} - (\gamma _1 + \gamma _2)I_{i3} - \mu I_{i3}\nonumber \\ \frac{dJ_{i1}}{dt}= & {} \eta _1G_{i1} + \gamma _2I_{i3} - (\gamma _1 + \mu )J_{i1}, \quad \quad \quad \quad \quad \quad \quad \quad \frac{dJ_{i2}}{dt} = \eta _2G_{i2} + \gamma _1I_{i3} - \gamma _2J_{i2} - \mu J_{i2}\nonumber \\ \frac{dR_{i1}}{dt}= & {} \gamma _1I_{i1} - d_{i2}R_{i1} - \mu R_{i1},\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \frac{dR_{i2}}{dt} = \gamma _2I_{i2} - d_{i1}R_{i2} - \mu R_{i2}\nonumber \\ \frac{dW_{i1}}{dt}= & {} \gamma _1K_{i1} - q_{i2}d_{i2}W_{i1} - \mu W_{i1}, \quad \quad \quad \quad \quad \quad \quad \quad \frac{dW_{i2}}{dt} = \gamma _2K_{i2} - q_{i1}d_{i1}W_{i2} - \mu W_{i2}\nonumber \\ \frac{dG_{i1}}{dt}= & {} d_{i1}R_{i2} + q_{i1}d_{i1}W_{i2} + \gamma _2L_{i2} - \eta _1G_{i1} - \mu G_{i1}\nonumber \\ \frac{dG_{i2}}{dt}= & {} d_{i2}R_{i1} + q_{i2}d_{i2}W_{i1} + \gamma _1L_{i1} - \eta _2G_{i2} - \mu G_{i2}\nonumber \\ \frac{dR_{i3}}{dt}= & {} \gamma _1J_{i1} + \gamma _2J_{i2} - \mu R_{i3}, \end{aligned}$$

(1)

where “$d_{i1}$” and “$d_{i2}$,” the infection rates, are given by

$$\begin{aligned} d_{i1}&= \sum _{m=1}^{2}\beta _{mi1}\frac{I_{m1}+K_{m1}+J_{m1}+L_{m1}+I_{m3}}{N},\\ d_{i2}&= \sum _{m=1}^{2}\beta _{mi2}\frac{I_{m2}+K_{m2}+J_{m2}+L_{m2}+I_{m3}}{N}. \end{aligned}$$

2.3.1 Case 1: Model with No Recruitment and Departure Rate

The system of nonlinear differential equations corresponding to the case one model is depicted in Fig. 3 for group i, $i=1,2$, without dotted arrows, and given by (1) for all $i=1,2$, with recruitment and departure rates are zeros. When $i=1$, $\Lambda _{1}=\mu =0$, (1) describe the compartments for the group one population, which represents pilgrims who are coming from the northern hemisphere. Group two population consisting of pilgrims coming from the southern hemisphere is described when $i=2$, $\Lambda _{2}=\mu =0$ in (1). Further, the initial conditions for all $i=1,2$ in case one model are described as

$$\begin{aligned} \frac{V_i(0)}{S_i(0)+V_i(0)} = \phi _i. \end{aligned}$$

There are at most few individuals in the other classes. This would make $V_i(0)$ approximately $\phi _i N_i$ and $S_i(0)$ approximately $(1-\phi _i)N_i$.

2.3.2 Case 2: Model with Constant Recruitment and Departure Rates

The system of nonlinear differential equations corresponding to the cases two and three is portrayed in Fig. 3 and given by (1), where recruitment rates ($\Lambda _{i}$, $i=1,2$) and departure rate ($\mu$) for the case two are going to be constant rates. We assume that strain one is only coming from northern pilgrims (green arrows in Fig. 3 and terms in (1)), and strain two from southern pilgrims (red arrows in Fig. 3 and terms only in (1)). Furthermore, there is a proportion of arriving infected pilgrims, namely prevalences of strain one and strain two are described as ($p_1$) and ($p_2$), respectively. Moreover, the distributions of infected states of the arriving pilgrims are evenly separated between infected ($p_i/2$) and exposed ($p_i/2$) compartments for both groups. Since infections are considered only to be among pilgrims, initial conditions for cases two and three are zero.

2.3.3 Case 3: Model with Non-Constant Recruitment and Departure Rates

Since the system of nonlinear differential equations corresponding to case three model is going to be similar to case two equations, with non-constant recruitment ($\Lambda _{i}$, $i=1,2$) and departure ($\mu$) rates, descriptions for the case three model will not be given. The case three model mirrors the actual timeline of the Hajj season, which has three phases. Phase one (arrival phase) occurs between day one and 38 of Hajj season, when individuals are arriving, and no one is leaving. Phase two (the Hajj worship phase) mainly happens between days 38 and 43 for the specific six days of the Hajj ritual, where everyone must be there to complete their rites. In other words, this phase represents the case one model, with no recruitment nor departure rates. Phase three (departure phase) mainly occurs between days 43 and the end of the season. All pilgrims must leave Saudi Arabia after the Hajj ritual no later than the 10th of Muharram of each year, which is 27 days after the Hajj ritual (US Department of State Bureau of Consular Affairs 2020). In this phase, pilgrims have ended their worship and ready to go back to their home country. Consequently, we will not have the departure rate ($\mu$) for phase one, and no recruitment rates ($\Lambda _{i}$,$i=1,2$) for phase three, while we will have neither recruitment rates nor departure rate for phase two. Thereupon, $\Lambda _i$ equals $\frac{N_i}{38}$, $i=1,2$ when t goes from 0 to 38, zero everywhere else, and $\mu$ represents the reciprocal of average time that pilgrims stay after Hajj worship ends, which we assume to be $\frac{1}{27}$ $\text {day}^{-1}$ for t between 44 and 90, and zero everywhere else (US Department of State Bureau of Consular Affairs 2020).

3 Analysis

Although equilibria have little practical meaning in a study of short-term dynamics, we nevertheless perform an equilibrium analysis in order to derive the control reproductive number (CRN), which is a measure of whether the disease would spread or not. We will study the infection’s ability to spread using CRN as a threshold quantity. It is called CRN instead of basic reproductive number (BRN) because it includes vaccination as a control measure. The point where the disease does not exist within the population is called disease-free equilibrium (DFE).

3.1 Control Reproduction Number for Case One Model

DFE occurs for the case one model equations when $I_{ij}=K_{ij}=L_{ij}=J_{ij}=I_{i3}=0$ $\forall$ $i,j = 1,2$. By setting all the nonlinear differential equations in case one model equations equal to zero, we get $E^*_{ij}=E^*_{i3}=F^*_{ij}=G^*_{ij}=0$ and infinitely many nonzero DFEs of the form DFE = ($S^*_{1}$,$S^*_{2}$,$V^*_{1}$,$V^*_{2}$,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 0,0,$R^*_{11}$,$R^*_{12}$,$R^*_{21}$,$R^*_{22}$,$R^*_{13}$, $R^*_{23}$,0,0,0,0,0,0,0,0,0,0,0,0, $W^*_{11}$,$W^*_{12}$,$W^*_{21}$,$W^*_{22}$), where $S^*_{i}$, $V^*_{i}$, $R^*_{ij}$, $R^*_{i3}$, $W^*_{ij}$ are free real valued variables $\forall$ $i,j = 1,2$ and

$$\begin{aligned} \sum _{j=1}^{2}[S^*_{i}+V^*_{i}+R^*_{ij}+R^*_{i3}+W^*_{ij}] = N_i. \end{aligned}$$

(If equilibrium components are required to take on whole-number values, then the number of equilibria is finite but very large). Although the next-generation methods normally assume an isolated disease free equilibrium, by Brauer and Castillo-Chavez (2001) it is sufficient to consider the disease free equilibrium where everyone is susceptible. In order to derive the control reproduction number (CRN), denoted by ${\mathcal {R}}_c$, for the case one model equations, we use the next-generation operator approach proposed by Diekmann et al. (1990). ${\mathcal {R}}_c$ is the spectral radius, the dominant eigenvalue, of the next-generation matrix (NGM) obtained from this method. Evaluating the NGM at DFE where everyone is susceptible, i.e., $R^*_{ij}+R^*_{i3}=W^*_{ij}=0$ for all $i, j = 1, 2$, and computing the spectral radius of the NGM, we have ${\mathcal {R}}_c =\smash {\displaystyle \max \{{\mathcal {R}}_1, \mathcal R_2\}}$ where:

$$\begin{aligned} {\mathcal {R}}_1&= \frac{\beta _{111}\tau _{11}+\beta _{221}\tau _{21}+\sqrt{(\beta _{111}\tau _{11}-\beta _{221}\tau _{21})^2+4\beta _{121}\beta _{211}\tau _{11}\tau _{21}}}{2\gamma _1},\\ {\mathcal {R}}_2&= \frac{\beta _{112}\tau _{12}+\beta _{222}\tau _{22}+\sqrt{(\beta _{112}\tau _{12}-\beta _{222}\tau _{22})^2+4\beta _{122}\beta _{212}\tau _{12}\tau _{22}}}{2\gamma _2}. \end{aligned}$$

$\tau _{ij}$ refers to the average susceptibility for strain j in group i. Then, by applying the initial conditions for case 1, we get

$$\begin{aligned} \tau ^*_{ij}&= \frac{S^*_i + q_{ij}V^*_i}{N_1+N_2}\\&= \frac{(1-\phi _{i})N_i+q_{ij}\phi _{ij}N_i}{N_1+N_2}\\&= \frac{(1-(1-q_{ij})\phi _i)N_i}{N_1+N_2}\\&= \sigma _{ij}n_i, \end{aligned}$$

where

$$\begin{aligned} n_i&= \frac{N_i}{N_1+N_2},\\ \sigma _{ij}&= 1-(1-q_{ij})\phi _i. \end{aligned}$$

3.2 Control Reproduction Number for Case Two Model

In order to compute CRN for case two model, we need to consider the special case when both $p_1$ and $p_2$ equal zero. In this matter, DFE occurs for the case two model equations when $I_{ij}=K_{ij}=J_{ij}=L_{ij}=I_{i3}=0$ $\forall$ $i,j = 1,2$. By setting all the equations equal to zero, we get DFE = ($(1-\phi _1)N^{*}_1$,$(1-\phi _2)N^{*}_2$,$\phi _1N^{*}_1$,$\phi _2N^{*}_2$,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0) and where for all $i=1,2$

$$\begin{aligned} N^{*}_i=\frac{\Lambda _i}{\mu }. \end{aligned}$$

Similarly, ${\mathcal {R}}_c$ for case 2 is calculated as the spectral radius of the NGM, where ${\mathcal {R}}_c =\smash {\displaystyle \max \{{\mathcal {R}}_1, {\mathcal {R}}_2\}}$ and

$$\begin{aligned} {\mathcal {R}}_1&=\frac{\eta _1}{\mu +\eta _1}\frac{\beta _{111}n^*_1\sigma _{11}+\beta _{221}n^*_2\sigma _{21}+\sqrt{(\beta _{111}n^*_1\sigma _{11}-\beta _{221}n^*_2\sigma _{21})^2+4\beta _{121}\beta _{211}n^*_1n^*_2\sigma _{11}\sigma _{21}}}{2(\mu +\gamma _1)},\\ {\mathcal {R}}_2&= \frac{\eta _2}{\mu +\eta _2} \frac{\beta _{112}n^*_1\sigma _{12}+\beta _{222}n^*_2\sigma _{22}+\sqrt{(\beta _{112}n^*_1\sigma _{12}-\beta _{222}n^*_2\sigma _{22})^2+4\beta _{122}\beta _{212}n^*_1n^*_2\sigma _{12}\sigma _{22}}}{2(\mu +\gamma _2)}, \end{aligned}$$

where for all $i, j = 1, 2$, we have:

$$\begin{aligned} n^*_i&=\frac{N^{*}_i}{N_1+N_2},\\ \sigma _{ij}&= 1-(1-q_{ij})\phi _i. \end{aligned}$$

Lemma 3.1

${\mathcal {R}}_c$’s are equal for both cases as long as $N_i$ approaches $N^*_i$ for all $i = 1, 2$ and $\mu$ goes to zero.

Proof

We notice that as $N_i$ approaches $N^*_i$ for all $i = 1, 2$, we get

$$\begin{aligned} \tau _{ij}&= \sigma _{ij}\frac{N_i}{N_1+N_2}\\&= \sigma _{ij}\frac{N^*_i}{N_1+N_2}\\&= \sigma _{ij}n^*_i. \end{aligned}$$

And as $\mu$ goes to zero, we have for all $i = 1, 2$

$$\begin{aligned} \frac{\eta _j}{\mu +\eta _j} = 1. \end{aligned}$$

$\square$

Following the text of Brauer and Castillo-Chavez (2001), we choose specifically the equilibrium where everyone is susceptible. By the initial conditions, we suppose that $S_i = (1-\phi _i)N_i$ and $V_i=\phi _i N_i$. From Lemma 3.1, we will have $\tau _{ij} = \sigma _{ij}n^*_i$. Then, the CRN for both cases will be $\mathcal R_c$ = $\max _{j}$ {${\mathcal {R}}_j\}$, $j=1,2$

$$\begin{aligned} {\mathcal {R}}_j = \frac{a_{11j} + a_{22j} + \sqrt{(a_{11j} - a_{22j})^2 + 4 a_{12j} a_{21j}}}{2}, \end{aligned}$$

and where

$$\begin{aligned} a_{mnj}&= {\left\{ \begin{array}{ll} \frac{\beta _{mnj}n^*_m\sigma _{mj}}{\gamma _j}&{}\quad \text {case 1}\\ \frac{\beta _{mnj}n^*_m\sigma _{mj}}{(\mu +\gamma _j)} &{}\quad \text {case 2}. \end{array}\right. } \end{aligned}$$

$a_{11j}$ refers to the transmission of influenza strain j within group one. Through pilgrims’ interaction, susceptible and a proportion of vaccinated pilgrims become infected by strain j, $j=1,2$. In a similar way, $a_{22j}$ describes the rate of development of infected individuals by strain j, $j=1,2$ in group 2 through contact with other individuals in group 2. Infected individuals from either group are recruited through interaction with other infected individuals from the same group, such as through accommodation in the same place or walking with nearby infected individuals from the same group. Both terms, $a_{11j}$ and $a_{22j}$, are the primary ways that influenza strain j develops within the system. The other recruitment is given by the terms $a_{12j}$ and $a_{21j}$. $a_{12j}$ is the transmission of strain j from an infected pilgrim from group 1 to an individual from group 2, and vice-versa $a_{21j}$. This occurs everywhere in Hajj due to the overcrowding in every holy site area. For each model, case 1 and case 2, the interpretation of the CRN for a strain j is the ability to spread. Strain j is spreading with efficiency $a_{11j}$ in population one and spreading with efficiency $a_{22j}$ in population two.

In order to interpret the CRN, we use two useful mathematical facts:

$$\begin{aligned} \sqrt{x+y}&\le \sqrt{x}+\sqrt{y},\\ \max \{x,y\}&= \frac{x+y+|x-y|}{2} \end{aligned}$$

Applying these facts to the CRN we have

$$\begin{aligned} \max _{1 \le k \le 2}\{a_{11j},a_{22j}\} \le {\mathcal {R}}_j \le \max _{1 \le k \le 2}\{a_{11j},a_{22j}\}+\sqrt{a_{12j}a_{21j}}]. \end{aligned}$$

The CRN is the ability of strain j to spread either in population one or in population two. It makes sense that ${\mathcal {R}}_c$ should be at least as great as its ability to spread in either population alone. In fact, it is greater because it is spreading in both populations. The square root is the geometric mean of the ability of strain j to spread from group one to group two and then back from group two to group one which is a complete cycle. Geometric mean is sort of the average of that ability to spread from group one to group two and then back or from group two to group one and then back. This is a form of ${\mathcal {R}}_0$ that has actually been seen lots of times before (Parikh et al. 2013).

To obtain the basic reproductive number (BRN) from the CRN, we set $\phi _i= 0$ for all $i=1,2$. By doing this we get BRN, $\mathcal R_0$ = $\max _{j}$ {${\mathcal {R}}_j\}$, $j=1,2$

$$\begin{aligned} {\mathcal {R}}_j = \frac{a^*_{11j} + a^*_{22j} + \sqrt{(a^*_{11j} - a^*_{22j})^2 + 4 a^*_{12j} a^*_{21j}}}{2}, \end{aligned}$$

and where

$$\begin{aligned} a^*_{mnj}&= \frac{\beta _{mnj}n^*_m}{\gamma _j}. \end{aligned}$$

3.3 Control Reproduction Number for Case Three Model

Since the case three model has three phases, it is not very easy to discuss the CRN. Furthermore, the first phase of the case three model has no equilibria; thus, we cannot compute CRN for the first phase. For the second phase, CRN is the same as the case one model. Additionally, all equilibria for phase three are extinction equilibria, which means CRN equals zero.

4 Parameter Estimates

To evaluate the impact of vaccine matching and mismatching, we provide some values of each parameter. Before estimating those values, we need to choose specific strains to consider. Since 1977, H1N1 and H3N2 have been co-circulating worldwide (Hsieh et al. 2005). Therefore, we take into account these two strains, respectively, in the model. Most of the model’s parameters can be estimated directly from the literature, with the only exception being the infection rates for which a more heuristic approach is required.

By carefully looking at studies of vaccination proportions in the last 20 years, we see a massive variation from basically no one to everyone. To make sense of this variation, despite there being some variation from country to country, however, what seems very important for us is variation by year. To that end, we notice that influenza 2009 pandemic temporarily and permanently changed the way people view influenza vaccination. So before 2009, the rate of influenza vaccine compliance was shallow, about 10.9% (Al-Maghderi et al. 2002; Nooh and Jamil 2004; AlMudmeigh et al. 2003; Kholeidi et al. 2001; Rashid et al. 2008a, b, c). Then, in 2009, the rate of compliance was very high. It was mandatory by Saudi Arabia for pilgrims from some countries to receive the vaccine to obtain the Hajj visa. The average rate of vaccine compliance from studies that we have seen with data in 2009 was about 95.7% (Al-Jasser et al. 2012; Moattari et al. 2012; Ziyaeyan et al. 2012; Gautret et al. 2010). After 2009, the compliance goes down, but it goes down to still a much higher level than before 2009. The average rate of vaccine compliance after 2009 was around 75% (Barasheed et al. 2014; Mohammad Hassan et al. 2013; Azeem et al. 2014).

To estimate the total number of northern and southern pilgrims, we examine individuals who attend Hajj based on their nationalities and the type of vaccine that has been recommended in their home countries. We obtain the total number of pilgrims from Saudi Arabia’s official records (Hajj Statistics 2019), and the type of recommended vaccine by WHO (WHO Influenza Vaccination Timing 2019), and then calculate the total number of pilgrims who came from countries where the vaccine is northern hemisphere vaccine and countries where the vaccine is southern hemisphere vaccine. The total estimate for the northern pilgrims ($N_1$) was 1771576, and that for the southern pilgrims ($N_2$) was 717830.

The estimation of the prevalence of influenza strain 1 (H1N1) among arrived pilgrims was 0.2% and 0.1% in Hajj season 2009 and 2013, respectively; strain 2 (H3N2) was 0.2% and 0.6% in Hajj season 2009 and 2013, respectively(Memish et al. 2011, 2015).

To estimate infection rates, we used a two-part process: first, relating different infection rates to each other and then applying a back-estimation approach to estimate the baseline values of each strain. We first observe that, for each strain, we have two distinct infection rates: cross-group $\beta _{mnj}$ and within-group infection rate $\beta _{mmj}$, for all $m,n,j=1,2$ and $m \ne n$. The nature of the contact while individuals are mixing, is different from the nature of contact while they are not mixing. For instance, several individuals sitting around a table, talking, or eating generates potentially infectious contacts, but not as many as when individuals are walking around the holy sites in the middle of intensive crowds. To relate the different infection rates for each strain, we must estimate how many hours per day individuals are mixing with individuals in the other group, sitting with their group, not mixing, and sleeping. We may assume that on average, individuals during Hajj spend 8 hours a day mixing with individuals in both groups, 8 hours a day sitting with their group, not mixing, and 8 hours a day sleeping. The kind of contact while they are mixing with individuals in the other group is so dense that their chance of getting infected is twice as high as when they are not mixing, for the same amount of time. Thereby, within-group infection rate ($\beta _{mmj}$) would be expected to be 50% more than the cross-group infection rate ($\beta _{mnj}$, $m\ne n$) because an individual would stay with his/her group while mixing with individuals in both groups or sitting with their group, not mixing. Consequently, we assume that cross-group infection rates ($\beta _{mnj}$, $m\ne n$) are the baseline rates for each strain, and $\beta _{12j}=\beta _{21j}$, $j=1,2$ (for simplification). Thus, the infection rates are reduced from eight different rates to two distinct baseline rates, one for each strain, and the other rates are described as follows: for all $m,j=1,2$, we have

$$\begin{aligned} \beta _{mmj} = 1.5 \beta _{12j}. \end{aligned}$$

The back-estimation approach is an inverse problem where first, we compute the basic reproductive number (${\mathcal {R}}_0$) for a simple SEIR model for each strain. For the simple SEIR model with no demographic change, ${\mathcal {R}}_j = \beta _{12j}/\gamma _j$. Then, by using the published values of ${\mathcal {R}}_0$ and $\gamma _j$ for each strain j, we calculate the baseline values of $\beta _{121}$ and $\beta _{122}$. The median value of ${\mathcal {R}}_0$ for strain 1 (H1N1) is set to 1.46, and strain 2 (H3N2) is set to 1.8 (Stehlé et al. 2011). Values for $\gamma _j$ are taken from Table 3. The resulting estimates for $\beta _{121}$ and $\beta _{122}$ are 0.4320 and 0.6570 $\text {days}^{-1}$, respectively. From these baseline values, we can estimate the other infection rates. Table 3 shows parameter values and the estimated values of infection rates.

Table 3 Summary of estimated model parameters

5 Numerical Simulations

Rites of pilgrimage can be completed between 5 and 6 days, beginning from the 8th of Dhu’l-Hijjah (12th month of Islamic Calendar), while the Hajj season starts on the first of Dhu’l-Qadah (11th month of Islamic Calendar), where pilgrims begin arriving in Saudi Arabia. In this section, we will consider the three cases: the first case is a simulation of the specific six days, where there are no recruitment nor departure rates. The case two model has pilgrims arriving and departing continuously. In this case, we will consider constant rates for recruitment and departure. The case three model has pilgrims arriving and departing during different periods. In this case, non-constant recruitment and departure rates will be considered.

To address the goal of this study, we separate the model’s compartments as susceptible, exposed, infected, and recovered for each strain. In this manner, the compartments that are susceptible to strain one (H1N1) are {$S_{1}$,$S_{2}$,$V_{1}$,$V_{2}$,$E_{12}$,$E_{22}$,$F_{12}$,$F_{22}$,$I_{12}$,$I_{22}$,$K_{12}$,$K_{22}$,$R_{12}$,$R_{22}$,$W_{12}$,$W_{22}$}, exposed to strain one are {$E_{11}$,$E_{21}$,$E_{13}$,$E_{23}$,$F_{11}$,$F_{21}$,$L_{12}$,$L_{22}$,$G_{11}$,$G_{21}$}, infected by strain one are {$I_{11}$,$I_{21}$,$K_{11}$,$K_{21}$,$L_{11}$,$L_{21}$,$I_{13}$,$I_{23}$, $J_{11}$,$J_{21}$} and recovered from strain one are {$R_{11}$,$R_{21}$,$W_{11}$,$W_{21}$,$G_{12}$,$G_{22}$,$J_{12}$,$J_{22}$, $R_{13}$,$R_{23}$}. Likewise, the compartments that are susceptible to strain two (H3N2) are {$S_{1}$,$S_{2}$,$V_{1}$,$V_{2}$,$E_{11}$,$E_{21}$,$F_{11}$,$F_{21}$,$I_{11}$,$I_{21}$,$K_{11}$,$K_{21}$,$R_{11}$,$R_{21}$,$W_{11}$,$W_{21}$}, exposed to strain two are {$E_{12}$,$E_{22}$,$E_{13}$,$E_{23}$,$F_{12}$,$F_{22}$,$L_{11}$,$L_{21}$,$G_{12}$,$G_{22}$}, infected by strain two are {$I_{12}$,$I_{22}$,$K_{12}$,$K_{22}$,$L_{12}$,$L_{22}$,$I_{13}$,$I_{23}$,$J_{12}$,$J_{22}$} and recovered from strain two are {$R_{12}$,$R_{22}$,$W_{12}$,$W_{22}$,$G_{11}$,$G_{21}$,$J_{11}$,$J_{21}$,$R_{13}$,$R_{23}$}.

Since the case one model is only applicable over six-day periods where pilgrims are not coming nor leaving, it could be considered a particular case of the model of the case three. We will not discuss the numerical simulation of case one here, but rather as part of the case three simulation.

Numerical simulation will be provided for the case two and three models with Sect. 4 parameter values, the post-2009 era for the proportion of individuals who have received the vaccine ($\phi _i$), and for the estimation of the prevalence of influenza strains one and two ($p_1$ and $p_2$).

5.1 Case Two Model: Constant Arrival and Departure Rates

Pilgrims start arriving in Saudi Arabia from the 1st day of the Hajj season (38 days before Hajj’s ritual started) till the 8th of Dhu’l-Hijjah, which is the day when all pilgrims gathered at Mena (a holy place near Makkah) to begin their pilgrimage journey. After the pilgrimage’s rites finish on the 13th day of Dhu’l-Hijjah, pilgrims begin to leave Makkah. Pilgrims may stay in Makkah until the Hajj season ends. In this matter, we divide the total number of northern pilgrims ($N_1$) and southern pilgrims ($N_2$) by the total number of arrival days (38 days), which gives us recruitment rates ($\Lambda _1$ and $\Lambda _2$). For the departure rate ($\mu$), since a pilgrim who comes on the first day of the Hajj season has to stay until the Hajj rites finish (on the 44th day of the Hajj season), we may assume that 44 days is the average time that pilgrims remain in Saudi Arabia.

Fig. 4

Case two: a Variations in mismatch rates ($q_{11}$ and $q_{21}$) against strain 1 (H1N1); b Variations in mismatch rates ($q_{22}$ and $q_{12}$) against strain 2 (H3N2); c For $q_{ij}$ $\forall i,j = 1,2$ in region I, no outbreak will occur for both strains; d For $q_{ij}$ $\forall i,j = 1,2$ in region II, a small outbreak will occur for both strains at the end of the Hajj season; e For $q_{ij}$ $\forall i,j = 1,2$ in region III, an outbreak will occur for both strains before everyone has gone home; f For $q_{22}$ and $q_{12}$ in region V, an outbreak will occur for H3N2 before Hajj ritual started, before day 38 of the Hajj season

We provide numerical simulations of case two model equations with constant recruitment and departure rates. Figure 4a and b indicates how variations in vaccine protections against strain 1 ($q_{11}$ and $q_{21}$) and strain 2 ($q_{22}$ and $q_{12}$) affect strain 1 and strain 2, respectively, outbreaks during the Hajj. The horizontal axis is the mismatch rate for the strain that the vaccine targets ($q_{ii}$), and ($1-q_{ii}$) represents the efficacy of the strain i. The vertical axis is the mismatch rate for the other strain, and ($1-q_{ij}$) represents the efficacy of the other strain. Figure 4a and b is created by incrementing the target strain mismatch rate $q_{ii}$ along the horizontal axis, and then for each value of $q_{ii}$ decreasing the non-target mismatch rate $q_{ij}$ along the vertical axis until the threshold behavior is observed for both strains. The first threshold, between regions I and II, is whether the outbreak occurs for both strains. This corresponds to the CRN equaling 1; below this threshold, although some new infections occur, increases come primarily from imported cases, and the numbers of cases for both strains are concave down over time (see Fig. 4c), unlike in the other regions. The second threshold is between regions II and III, where the peak of the outbreak occurs on day 66 for both strains. The third threshold is between regions III and IV for strain two only, where the peak of the outbreak occurs on day 44. The fourth threshold is between regions IV and V for strain two only, where the peak of the outbreak occurs on day 38. We assume that the efficacy of the target strain is better than the efficacy of the other strain (i.e., $q_{ij} > q_{ii}$ for all i, j=1, 2). With this in mind, our attention will be restricted above the diagonal line of Fig. 4a and b. Figure 4c–f gives a time series of data of infections over time for a given strain.

Figure 4a and b consists of the final results of strain 1 (H1N1) and strain 2 (H3N2), respectively, spread simulations with different amounts of mismatching reduced rates ($q_{ij}$). They show that there are three regions for strain 1 (H1N1) and five regions for strain 2 (H3N2) for the peak of the absolute number of cases. Under the conditions in region I, there is no outbreak, and both strains will go extinct for any value of mismatching reduced rates ($q_{ij}$) in this region (see Fig. 4c). The relatively low infection level in Fig. 4c is caused by constant importation of infectives from the two hemispheres. This behavior does not represent an outbreak because the growth is not due to transmission, but to direct importation of infection. For parameter values in region II, there is a small outbreak which peaks at the end of the season between day 66 and day 90 of the Hajj season (see Fig. 4d). For parameter values in region III, there is an outbreak that peaks after Hajj rites and before everyone goes back to their home country between day 44 and day 66 (see Fig. 4e). For parameter values in region IV, there is an outbreak that peaks during Hajj rites, which is between day 38 and day 44 of the Hajj season, where all pilgrims are arrived and practicing their rituals. For parameter values in region V, there is an outbreak that peaks before Hajj rites started and before all pilgrims have arrived, which is between day 35 and day 38 of the Hajj season (see Fig. 4f). Hence, unless the vaccine efficacy is enormously high, there will be an outbreak of both influenza strains. Approximately, the peak of an outbreak will occur before pilgrims return to their home country if the vaccine efficacy is between 0% to 40% strain 2 (H3N2), and 0% to 10% for strain 1 (H1N1). Otherwise, if the vaccine efficacy is between 40% to 80%, the peak of an outbreak will occur after pilgrims have gone home.

Fig. 5

Case three: a and b Variations in mismatch rates ($q_{11}$ and $q_{21}$) and ($q_{22}$ and $q_{12}$) against H1N1 and H3N2, respectively; c–f prevalence, g–j the absolute number of cases of H1N1 and H3N2, respectively, for varying values of $q_{ii}$ and $q_{ij}$ $\forall i,j = 1,2$ and $i\ne j$

5.2 Case Three Model: Non-Constant Arrival and Departure Rates

Figure 5a and b were generated similar to Fig. 4a and b and indicate the different result regions for each strain for varying values of $q_{ii}$ and $q_{ij}$ $\forall i,j = 1,2$ and $i\ne j$. Figure 5c–j shows the strain 1 (H1N1) and strain 2 (H3N2) simulation with different $q_{ij}$, $i,j=1,2$. The upper and lower figures of 5c–f and g–j indicate the prevalence and the absolute number of cases, respectively, for H1N1 and H3N2.

For parameter values in region I, there is no outbreak for both strains and they will become extinct, since this region represents the values of $q_{ij}$, $i,j=1,2$ such that CRN (for phase two) is less than one (see Fig. 5c). For parameter values in region II, the peak of the absolute number of cases occurs on the last day of the Hajj worship phase, day 43, (see Fig. 5h), and the peak of prevalence occurs on last days of Hajj season, between days 60 and the end of the season (see Fig. 5d). For the parameter values in region III, there is an outbreak whose peaks of the absolute number of cases and prevalence occur after the Hajj worship phase, between day 43 and end of the season (see Fig. 5e, i). For the parameter values in region IV for H3N2, there is an outbreak whose peaks of the absolute number of cases and prevalence occur at the same time during Hajj ritual time, between days 38 and 43 (see Fig. 5f, j). For the parameter values in region V for H3N2, there is an outbreak whose peak of the absolute number of cases and prevalence occur during the arrival phase, between days 33 and 37.

For all parameter values ($q_{ij}$) in all regions, except region I, there will be an outbreak of both strains of influenza. If vaccine efficacy ($1-q_{ij}$) for $q_{ij}$ is in region II, then the peak of an outbreak of the absolute number of cases occurs in the Hajj worship phase (see Fig. 5h), and the peak of prevalence occurs in the departure phase (see Fig. 5d). The peak of an outbreak will occur in the departure phase for both strains on the condition that the vaccine efficacy ($1-q_{ij}$) for parameter values $q_{ij}$ lies in region III (see Fig. 5e, i). In the sequel, the peak of an outbreak will occur in the worship phase and the arriving phase for H3N2 if the vaccine efficacy ($1-q_{ij}$) for parameter values ($q_{22}$ and $q_{12}$) lies in regions IV and V, respectively (see Fig. 5f, j).

6 Discussion and Conclusions

Mathematical models are useful in forecasting disease dynamics and estimating significant parameters that can be incorporated to resist the spread of disease. This study analyzed deterministic models for two populations and two strains of influenza to evaluate the impact of mismatch between influenza vaccine strains and circulating strains.

Based on this work, an outbreak occurs for both strains unless the vaccine’s effectiveness is tremendously high for both populations (see Figs. 4c and 5c). Whether we have an outbreak at the end of Hajj season (see Fig. 4d), during the Hajj ritual (see Fig. 5h), or even before that (see Figs. 4f and 5j), depends on the vaccine’s efficacy. When the case three model is considered, our results show that the peak of the absolute number of cases occurs at the end of the Hajj ritual (the Hajj worship phase) for region II for both strains with low prevalence at the end of the Hajj season. Further, if the mismatch rates for both strains fall in region III, then the peak of absolute numbers of cases and prevalence occurs in the departure phase (see Fig. 5e). Nonetheless, for extremely low vaccine efficacy (between 0% to 20% for strain H3N2), we have a severe outbreak that occurs during or a couple of days before the Hajj ritual (see Fig. 5j).

We study the CRN for the case one model, which is equivalent to phase two (the Hajj worship phase) of the case three model. We show that any outbreak will be in the process of dying out during phase two as long as the amount of mismatch reduced rates ($q_{ij}$) is within region I (see Fig. 5c), which indicates that CRN is less than one. When CRN is greater than one, we introduce region II, where averaged CRN is between 1 and 1.32 for strain 1 (H1N1) and between 1 and 1.36 for strain 2 (H3N2). In this region, any outbreak will peak during the Hajj worship phase (see Fig. 5h), with low prevalence peak at the last days of the Hajj season (see Fig. 5d). Additionally, in region III, the averaged CRN is between 1.32 and 1.90 for H1N1 and between 1.36 and 2.11 for H3N2. In this region, an outbreak will occur in the departure phase, with a peak of prevalence at the same phase (see Fig. 5i). Ultimately, regions IV (see Fig. 5f, j) and V for H3N2 only exhibit CRN values between 2.11 and 2.50, respectively. In these regions, a severe outbreak will occur in phase two (during Hajj ritual) for region IV and during the last days of the arrival phase for region V.

In conclusion, the existence and time of an outbreak of influenza in Hajj depend on mismatch reduced rates ($q_{ij}$). In this situation, we may have different possible outcomes. The best scenario has vaccine strains for both groups well match circulating strains, where averaged vaccine effectiveness (VE) will be 71% (57% to 86%). In this scenario, mismatch reduced rates will range from 0.14 to 0.43, with an average of 0.29, which places us in region I for H1N1 and region II for H3N2. Hence, there will be no outbreak for H1N1, and a small outbreak for H3N2 whose peak of the absolute number of cases occurs on the last day of the Hajj worship phase, causing approximately 6500 new infections. Another scenario has vaccine strains match their target strains and mismatch the other strains. In this instance, average $q_{ii}$ and $q_{ij}$ will be 0.29 and 0.43, respectively ($\forall i,j=1,2, i \ne j$), which places us at the same regions and peak occurrence for H1N1 and H3N2 with approximately 10,000 additional infections for H3N2 than the first scenario. Furthermore, we consider a scenario in which both strains included in the influenza vaccine for both groups mismatch circulating strains, where averaged VE will be 57% (43% to 71%). Under these circumstances, mismatch reduced rates will range from 0.29 to 0.57, with an average of 0.43, which places us in region II for H1N1 and region III for H3N2. Consequently, there will be an outbreak for both strains that peaks on the last day of the Hajj worship phase with 2000 new cases for H1N1, and at the departure phase with approximately 6000 more infections for H3N2 than the second scenario. These numbers represent cases in Saudi Arabia during Hajj before pilgrims leave. Additional numbers of cases will arise in the pilgrims’ home countries.

However, if the next influenza pandemic arrives, then the VE would be at its worst case, and the seasonal vaccine will have no protection against novel pandemic strains (Kelly and Grant 2009). Hence, vaccination rates ($\phi _1$ and $\phi _2$) are irrelevant. In that connection, we may witness a severe outbreak for H3N2 that peaks before everyone has arrived in Makkah (regions IV and V) with approximately 235,500 additional infections, and for H1N1 that peaks after the Hajj worship phase and before everyone returns home (regions III) with approximately 116,000 additional infections (including over 9,000 co-infections).

As long as the influenza vaccines match their target strains, there will be no outbreak of strain H1N1, and only a small outbreak of strain H3N2. In the case of mismatching for non-target strains, it causes about 10,000 new H3N2 cases. In the case of mismatching for both strains, it causes about 2,000 new H1N1 cases and 6,000 additional H3N2 cases. Complete mismatch in a pandemic scenario may infect over 342,000 additional pilgrims (13.75%) and cause more cases in their home countries. These numbers could help the Saudi Ministry of Health (Saudi MOH) to estimate what additional primary health facilities are needed. Besides the size of an expected outbreak, Saudi MOH could make the influenza vaccine mandatory for all pilgrims in order to obtain a Hajj VISA. Further, Saudi MOH could require all arriving pilgrims to pass a health screening before entering the country in order to minimize the number of infected pilgrims.

Our findings can help decision-makers to assess the risk of mismatching between the influenza vaccine and circulating strains and choose containment strategies to mitigate an outbreak. However, the results are limited by the assumption that pilgrims from the northern/southern hemisphere have the same exposure. The heterogeneity of individuals arriving for Hajj is more than merely whether they come from the northern/southern hemisphere. Further, the amount of data available to estimate parameter values was limited, and our parameter estimates could be better if we have more data to estimate. In the future, a model can be developed to include more heterogeneity in the arriving populations, such as tropical vs. temperate zones. Our model can also be extended to include several strains to apply to a broader range of influenza viruses. Furthermore, a clinical work can be done to examine how genetically closely related two influenza strains must be in order for the vaccine for one strain to make an individual more susceptible to the other strain.