Traveling Waves and Estimation of Minimal Wave Speed for a Diffusive Influenza Model with Multiple Strains

Abstract

Antiviral treatment remains one of the key pharmacological interventions against influenza pandemic. However, widespread use of antiviral drugs brings with it the danger of drug resistance evolution. To assess the risk of the emergence and diffusion of resistance, in this paper, we develop a diffusive influenza model where influenza infection involves both drug-sensitive and drug-resistant strains. We first analyze its corresponding reaction model, whose reproduction numbers and equilibria are derived. The results show that the sensitive strains can be eliminated by treatment. Then, we establish the existence of the three kinds of traveling waves starting from the disease-free equilibrium, i.e., semi-traveling waves, strong traveling waves and persistent traveling waves, from which we can get some useful information (such as whether influenza will spread, asymptotic speed of propagation, the final state of the wavefront). On the other hand, we discuss three situations in which semi-traveling waves do not exist. When the control reproduction number $R_{C}$ is larger than 1, the conditions for the existence and nonexistence of traveling waves are determined completely by the reproduction numbers $R_{SC}$, $R_{RC}$ and the wave speed c. Meanwhile, we give an interval estimation of minimal wave speed for influenza transmission, which has important guiding significance for the control of influenza in reality. Our findings demonstrate that the control of influenza depends not only on the rates of resistance emergence and transmission during treatment, but also on the diffusion rates of influenza strains, which have been overlooked in previous modeling studies. This suggests that antiviral treatment should be implemented appropriately, and infected individuals (especially with the resistant strain) should be tested and controlled effectively. Finally, we outline some future directions that deserve further investigation.

1 Introduction

Influenza is a serious cytopathogenic, drastic respiratory infectious disease that is caused by an RNA virus in the Orthomyxoviridae family (Earn et al. 2002; Möhler et al. 2005). Based on the differences in two major internal proteins, matrix protein (M) and nucleoprotein (NP), the virus is categorized into three main types: A, B and C (Webster et al. 1992; Tamura et al. 2005). Influenza virus can be transmitted among human beings in various ways, such as direct contact with infectious individuals, by contact with contaminated objects, by inhalation of virus-laden aerosols, etc (Viboud et al. 2004).

In fact, human influenza, a more severe disease, has been a major cause of excessive morbidity and mortality: 40 million in Spanish flu (H1N1) 1918–1919 (Oxford 2000) and a total of 6 million in Asian flu (H2N2) 1957–1958 and Hong-Kong flu (H3N2) 1968 (Stone et al. 2007). In particular, the outbreak of 2009 H1N1 flu (swine flu) has proved again that influenza can be a serious problem worldwide (Garten et al. 2009). In addition, influenza poses a considerable economic burden of society and becomes a problem of public health (Webster et al. 1992). Therefore, it is imperative to study how to prevent and contain the outbreak of influenza, increasing our understanding of the influenza transmission dynamics.

To prevent and control pandemic influenza, various pharmaceutical (vaccination and antiviral treatment) and non-pharmaceutical (wearing masks, reducing the frequency of going out or paying attention to personal hygiene) measures (Longini et al. 2005; Ferguson et al. 2005; Halloran et al. 2008) may be taken. Among pharmaceutical interventions, antiviral treatment (including a range of medications and therapies) remains one of the most effective measures to lower disease transmission and reduce the health burden of infections (Ferguson et al. 2005). However, abundant use of antiviral drugs (such as oseltamivir and zanamivir) is a significant factor in producing resistant strains. The emergence of drug-resistant strains prevents the growth and spread of the drug-sensitive strains, which has raised great concern for public health (Heymann 2006).

More recently, some mathematical models (primarily ordinary differential, networked and stochastic models), as effective tools, have explored the potential effects of drug resistance on the transmission of influenza (Stilianakis et al. 1998; Regoes and Bonhoeffer 2006; Moghadas et al. 2008) and identified effective treatment strategies for resistance management (Lipsitch et al. 2007; Moghadas 2008; Moghadas et al. 2009; Qiu and Feng 2010; Hansen and Day 2011). For example, Lipsitch et al. (2007) designed and analyzed a deterministic compartmental model of the transmission of oseltamivir-sensitive and -resistant influenza infections during a pandemic. They concluded that the benefits of antiviral drug use to control an influenza pandemic may be reduced, although not completely offset, by drug resistance in the virus. Jnawali et al. (2016) developed and analyzed a classical two-player game theoretical model where each player chooses from a range of possible rates of antiviral drug use, and payoffs are derived as a function of final size of epidemic with the regular and mutant strain. Their results showed that strategic interactions could strongly influence a population’s choice of antiviral drug use policy.

If the random movement of individuals in space plays a very important role in the dynamics of influenza transmission, it is necessary to consider the influence of spatial diffusion, which is usually characterized by reaction–diffusion equations. Zhang and Wang (2014) established a reaction–diffusion influenza model with treatment and focused on the existence and nonexistence of traveling wave solutions. Xu and Ai (2016) formulated a mathematical model of influenza disease with vaccination to incorporate a spatially homogeneous structure. It is shown that the existence and nonexistence of the traveling wave solutions for the model are determined completely by the basic reproduction number.

These studies have provided much useful insights into the emergence, spread and control of influenza. However, most of these models have considered either antiviral use or the spatial structure of large populations alone. The potential large-scale use of antiviral drugs brings with it the danger of drug resistance diffusion, which will create an unprecedented selective pressure for the control of pandemic influenza. To assess the impact of antiviral resistance and population diffusion, in this paper, we modify and extend a previous model of influenza epidemic into a diffusive model which takes into account the division of large populations into smaller units, the effects of demographic processes (recruitment and natural deaths) and spatial diffusion factors. The new model allows us to examine the effects of antiviral use on the prevalence of both drug-sensitive and drug-resistant strains under the influence of population diffusion and to explore the interaction between populations considering antiviral drug use strategies.

To this end, we develop a diffusive influenza model with multiple strains includes explicitly both antiviral use and spatial diffusion in Sect. 2. The equilibria and reproduction numbers for the corresponding reaction model are discussed in Sect. 3. The existence of three different kinds of traveling waves of the diffusive model is established in Sect. 4. The conditions for the nonexistence of semi-traveling waves of the diffusive model and the estimation of minimal wave speed are given in Sect. 5. Finally, some further discussions are listed in Sect. 6 to conclude this work.

2 A Diffusive Influenza Model With Multiple Strains

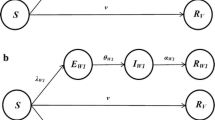
We adapt the approach of Lipsitch et al. (2007) for modeling the drug treatment (without prophylaxis). In a homogeneously mixing population, individuals may be treated with antiviral drugs, or not treated. They may also be either infected with the regular drug- sensitive strain, or with the mutant drug resistance strain. Then, a population is divided into classes of individuals with epidemiological statuses as susceptible (S), infected with the sensitive strain $(I_{SU})$, infected with the sensitive strain under treatment $(I_{ST})$, infected with the resistant strain $(I_{R})$ and recovered individuals (R). To describe the spatiotemporal spreading behavior between susceptible and infectious individuals, we extend their ordinary differential equation (ODE) model by including diffusion terms and vital dynamics (recruitment and mortality). Therefore, a diffusive influenza model with multiple strains can be demonstrated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial S}{\partial t} = d_{S}\frac{\partial ^{2} S}{\partial x^{2}}+\varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ \frac{\partial I_{SU}}{\partial t} = d_{SU}\frac{\partial ^{2} I_{SU}}{\partial x^{2}}+(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU}, \\ \frac{\partial I_{ST}}{\partial t} = d_{ST}\frac{\partial ^{2} I_{ST}}{\partial x^{2}}+f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST}, \\ \frac{\partial I_{R}}{\partial t} = d_{R}\frac{\partial ^{2} I_{R}}{\partial x^{2}}+[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S-(k_{R}+\mu )I_{R}, \\ \frac{\partial R}{\partial t} = d_{\widetilde{R}}\frac{\partial ^{2} R}{\partial x^{2}}+k_{U}I_{SU}+k_{T}I_{ST}+k_{R}I_{R}-\mu R, \end{array}\right. \end{aligned}$$

(1)

where $S(x,t), I_{SU}(x,t), I_{ST}(x,t), I_{R}(x,t)$ and R(x, t) represent the quantities of susceptible, infected with the sensitive strain and untreated, infected with the sensitive strain and treated, infected with the resistant strain and recovered population at position x and time t, respectively. The parameters $d_{S}, d_{SU}, d_{ST}, d_{R}$ and $d_{\widetilde{R}}$ are the diffusion coefficients of the above five subclasses. The constant $\varLambda$ is the recruitment rate of the population and $\mu$ is per capita natural death rate. Here we assume that each infected individual with the sensitive strain will receive treatment with proportion f, and each individual who received treatment will develop drug resistance with probability r. The parameters $\beta _{S}$ and $\beta _{R}$ are the transmission coefficients of the untreated and drug-resistant infected individuals. Due to antiviral treatment, the transmission rate by an individual who received treatment will be reduced by the factor $\delta$. Each individual in $I_{j}$ subclasses can recover with the corresponding rate $k_{j}$, $j = SU, ST, R$. All parameters are assumed to be positive.

Since the first four equations of (1) are independent of the last one, it suffices to consider the following reduced reaction–diffusion system:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial S}{\partial t} = d_{S}\frac{\partial ^{2} S}{\partial x^{2}}+\varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ \frac{\partial I_{SU}}{\partial t} = d_{SU}\frac{\partial ^{2} I_{SU}}{\partial x^{2}}+(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU}, \\ \frac{\partial I_{ST}}{\partial t} = d_{ST}\frac{\partial ^{2} I_{ST}}{\partial x^{2}}+f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST}, \\ \frac{\partial I_{R}}{\partial t} = d_{R}\frac{\partial ^{2} I_{R}}{\partial x^{2}}+[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S-(k_{R}+\mu )I_{R}. \end{array}\right. \end{aligned}$$

(2)

3 Equilibria and Reproduction Numbers for the Reaction Model

When the spatial diffusion of population is omitted, the diffusive model (1) is reduced to a reaction model. Sometimes it greatly affects the dynamics of its diffusion model (Gardner 1984), so it is necessary to analyze the reaction model of model (1), which is described by the following system of ODEs:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\mathrm{d} S}{\mathrm{d} t} = \varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ \frac{\mathrm{d} I_{SU}}{\mathrm{d} t} = (1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU}, \\ \frac{\mathrm{d} I_{ST}}{\mathrm{d} t} = f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST}, \\ \frac{\mathrm{d} I_{R}}{\mathrm{d} t} = [fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S-(k_{R}+\mu )I_{R}, \\ \frac{\mathrm{d} R}{\mathrm{d} t} = k_{U}I_{SU}+k_{T}I_{ST}+k_{R}I_{R}-\mu R. \end{array}\right. \end{aligned}$$

(3)

In this section, we give a brief discussion about the existence of equilibria and reproduction numbers of the reaction model (3).

Denote by $N(t) = S(t)+I_{SU}(t)+I_{ST}(t)+I_{R}(t)+R(t)$, the total quantity of the population at time t. Note that N(t) satisfies the equation $\frac{\mathrm{d} N}{\mathrm{d} t} = \varLambda -\mu N,$ which, for any initial value $N(t_{0})\ge 0$, has a general solution of the form

$$\begin{aligned} \begin{array}{l} N(t)=\frac{1}{\mu }[\varLambda -(\varLambda -\mu N(t_{0}))\exp ^{-\mu (t-t_{0})}]. \end{array} \end{aligned}$$

Then, we have $\lim _{t\rightarrow +\infty }N(t)=\frac{\varLambda }{\mu }$. Through the above analysis, we know that the biologically feasible set of the reaction model (3) is given by

$$\begin{aligned} \varGamma =\left\{ (S, I_{SU}, I_{ST}, I_{R}, R)|0\le S, I_{SU}, I_{ST}, I_{R}, R, S+I_{SU}+I_{ST}+I_{R}+R\le \frac{\varLambda }{\mu }\right\} . \end{aligned}$$

Obviously, the set $\varGamma$ is positively invariant for the reaction model (3).

There is a key parameter in epidemiological models, the basic reproduction number, commonly denoted by $R_{0}$, defined as the expected number of secondary infections generated by a single infectious individual during the infection period in an entirely susceptible population (Anderson et al. 1992; Diekmann and Heesterbeek 2000; Hethcote 2000). When certain control measures (such as immunization, isolation, treatment, etc) are introduced, we use the control reproduction number, denoted by $R_{C}$, to determine whether the epidemic can be contained (Anderson et al. 1992).

Similar to the calculation of the basic reproduction number, we can use the same approach developed in Diekmann and Heesterbeek (2000) and Van den Driessche and Watmough (2002) to calculate the control reproduction number of the reaction model (3) with treatment terms. Note that the reaction model (3) always has a disease-free equilibrium $E^{0} = (S^{0},0,0,0,0)$, where $S^{0}:= \frac{\varLambda }{\mu }$. The reaction model (3) has three infected variables, namely $I_{SU}, I_{ST}$ and $I_{R}$, linearizing the equations of these three variables at the equilibrium $E^{0}(S^{0},0,0,0,0)$, the matrices F and V (corresponding to the new infection and remaining transfer terms, respectively) are given by

$$\begin{aligned} F=\left( \begin{array}{cccc} (1-f)\beta _{S}S^{0} &{} (1-f)\beta _{S}\delta S^{0} &{} 0 \\ f(1-r)\beta _{S}S^{0} &{} f(1-r)\beta _{S}\delta S^{0} &{} 0 \\ fr\beta _{S}S^{0} &{} fr\beta _{S}\delta S^{0} &{} \beta _{R}S^{0} \\ \end{array} \right) , \end{aligned}$$

(4)

and

$$\begin{aligned} V=\left( \begin{array}{cccc} k_{U}+\mu &{} 0 &{} 0 \\ 0 &{} k_{T}+\mu &{} 0 \\ 0 &{} 0 &{} k_{R}+\mu \\ \end{array} \right) . \end{aligned}$$

(5)

Thus, $FV^{-1}=\left( \begin{array}{cccc} F_{11} &{} 0 \\ F_{21} &{} F_{22} \\ \end{array} \right) ,$ where

$$\begin{aligned} F_{11}=\left( \begin{array}{cccc} \frac{(1-f)\beta _{S}S^{0}}{k_{U}+\mu } &{} \frac{(1-f)\beta _{S}\delta S^{0}}{k_{T}+\mu } \\ \frac{f(1-r)\beta _{S}S^{0}}{k_{U}+\mu } &{} \frac{f(1-r)\beta _{S}\delta S^{0}}{k_{T}+\mu } \\ \end{array} \right) ,\quad F_{21}=\left( \begin{array}{cccc} \frac{fr\beta _{S}S^{0}}{k_{U}+\mu } &{} \frac{fr\beta _{S}\delta S^{0}}{k_{T}+\mu } \\ \end{array} \right) ,\quad F_{22}=\frac{\beta _{R}S^{0}}{k_{R}+\mu }. \end{aligned}$$

Let

$$\begin{aligned} R_{SU}=\frac{\beta _{S}}{k_{U}+\mu },\quad R_{ST}=\frac{\beta _{S}\delta }{k_{T}+\mu },\quad R_{R}=\frac{\beta _{R}}{k_{R}+\mu }, \end{aligned}$$

(6)

then we have

$$\begin{aligned} R_{SC}=\rho (F_{11})=\frac{(1-f)\beta _{S}S^{0}}{k_{U}+\mu }+\frac{f(1-r)\beta _{S}\delta S^{0}}{k_{T}+\mu }=S^{0}[(1-f)R_{SU}+f(1-r)R_{ST}], \end{aligned}$$

(7)

and

$$\begin{aligned} R_{RC}=\rho (F_{22})=\frac{\beta _{R}S^{0}}{k_{R}+\mu }=S^{0}R_{R}, \end{aligned}$$

(8)

where $\rho (A)$ is the spectral radius of the nonnegative matrix A.

Therefore, the control reproduction number of the reaction model (3) is given by

$$\begin{aligned} R_{C}=\rho (FV^{-1})=\max \{R_{SC}, R_{RC}\}. \end{aligned}$$

(9)

The biological interpretations of these quantities are as follows. Note that $R_{SC}$ represents the number of secondary sensitive cases that one individual infected with the sensitive strain initiates in a completely susceptible population where antiviral treatment is implemented, while $R_{RC}$ represents the number of secondary resistant cases that one individual infected with the resistant strain initiates in a completely susceptible population. The quantity $R_{SC}$ consists of two parts: $(1-f)S^{0}R_{SU}$ and $f(1-r)S^{0}R_{ST}$, which represent the numbers of secondary sensitive cases produced by a untreated and treated sensitive case during the period of infection in a susceptible population, respectively. In the influenza context, the control reproduction number $R_{C}$ tells us, on average, the total number of individuals that each single infected individual will initiate to influenza virus during the period of infection in a completely susceptible population.

The above quantities can be used to investigate the existence of equilibria of the reaction model (3), so we present the following lemma.

Lemma 3.1

• (1) The disease-free equilibrium $E^{0}$ always exists;

• (2) If $R_{C} < 1$, there exists a unique disease-free equilibrium $E^{0}$;

• (3) If $R_{C} > 1$, then in addition to the disease-free equilibrium $E^{0}$, the reaction model (3) has a boundary equilibrium $\hat{E}$ when $R_{RC} > 1$, and an interior (positive) equilibrium $E^{*}$ when $R_{SC} > 1$ and $R_{RC} < R_{SC}$.

Proof

The equilibria of the reaction model (3) are the solutions of the following equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S = 0, \\ (1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU} = 0, \\ f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST} = 0, \\ \left[ fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}\right] S-(k_{R}+\mu )I_{R} = 0, \\ k_{U}I_{SU}+k_{T}I_{ST}+k_{R}I_{R}-\mu R = 0. \end{array}\right. \end{aligned}$$

(10)

In order to solve algebraic Eq. (10), we divide it into the following three cases.

Case I: $I_{R} = 0$. For this case, based on the setting of parameters and the fact that $S >0$, from the fourth equation of (10), we have $I_{SU} = I_{ST} = 0$. Substituting $I_{R} = I_{SU} = I_{ST} = 0$ into the first equation of (10), we can obtain $S = \frac{\varLambda }{\mu } = S^{0}$.

Case II: $I_{R} > 0$ and $I_{ST} = 0$. For this case, it follows from the third and fourth equations of (10) that $I_{SU} = 0$ and $S = \frac{k_{R}+\mu }{\beta _{R}} = \frac{S^{0}}{R_{RC}} := \hat{S}$. Substituting $I_{SU} = I_{ST} = 0$ and $S = \hat{S}$ into (10), we get the following reduced equations

$$\begin{aligned} \varLambda -\mu \hat{S}-\beta _{R}I_{R}\hat{S} = 0, \quad k_{R}I_{R}-\mu R = 0. \end{aligned}$$

(11)

By solving linear algebraic Eq. (11), we obtain $I_{R} = \frac{\mu S^{0}\left( 1-\frac{1}{R_{RC}}\right) }{k_{R}+\mu } := \hat{I}_{R}$ and $R = \frac{k_{R} S^{0}\left( 1-\frac{1}{R_{RC}}\right) }{k_{R}+\mu } := \hat{R}$.

Case III: $I_{R} > 0$ and $I_{ST} > 0$. For this case, we first deal with the second and third equations of (10), which can be regarded as equations with unknown quantities $I_{SU}$ and $I_{ST}$. In view of the fact that $I_{ST} > 0$, by Cramer’s Rule, we have

$$\begin{aligned} \left| \begin{array}{cccc} (1-f)\beta _{S}S-(k_{U}+\mu ) &{} (1-f)\beta _{S}\delta S \\ f(1-r)\beta _{S}S &{} f(1-r)\beta _{S}\delta S-(k_{T}+\mu ) \\ \end{array} \right| =0. \end{aligned}$$

Calculate the above determinant, we can get the value of S as follows

$$\begin{aligned} S=\frac{(k_{U}+\mu )(k_{T}+\mu )}{(k_{T}+\mu )(1-f)\beta _{S}+(k_{U}+\mu )f(1-r)\beta _{S}\delta } = \frac{S^{0}}{R_{SC}} := S^{*}. \end{aligned}$$

Substituting $S = S^{*}$ into (10), after some algebraic computations, we can solve the remaining four unknown quantities of Eq. (10) with $S = S^{*}$ as follows

$$\begin{aligned} \begin{array}{ll} I_{SU} = \frac{\mu (R_{SC}-1)}{\beta _{S}(1+\delta a)+\beta _{R}b} := I^{*}_{SU},&{}\quad I_{ST} = aI^{*}_{SU} := I^{*}_{ST}, \\ I_{R} = bI^{*}_{SU} := I^{*}_{R},&{}\quad R = \frac{k_{U}I^{*}_{SU}+k_{T}I^{*}_{ST}+k_{R}I^{*}_{R}}{\mu } :=R^{*}, \end{array} \end{aligned}$$

where $a=\frac{f(1-r)(k_{U}+\mu )}{(1-f)(k_{T}+\mu )}$ and $b=\frac{fr(k_{U}+\mu )}{(1-f)(k_{R}+\mu )(1-\frac{R_{RC}}{R_{SC}})}$.

From the above discussions, it follows that (10) has three possible nonnegative solutions. Accordingly, the reaction model (3) has three possible equilibria $E^{0} = (S^{0},0,0,0,0)$, $\hat{E} = (\hat{S},0,0,\hat{I}_{R},\hat{R})$ and $E^{*} = (S^{*}, I^{*}_{SU}, I^{*}_{ST}, I^{*}_{R}, R^{*})$. Based on the expression of $\hat{I}_{R}$ in Case II, we know that $\hat{I}_{R}>0$ if and only if $R_{RC}>1$. Under the condition $I^{*}_{SU}>0$, from the expression of $I^{*}_{R}$ in Case III, we can easily see that $I^{*}_{R}>0$ if and only if $R_{RC} < R_{SC}$, which implies $b>0$. Return to the expression of $I^{*}_{SU}$, we can similarly determine that $I^{*}_{SU}>0$ if and only if $R_{SC}>1$. When $R_{C} < 1$, i.e., $R_{SC}<1$ and $R_{RC}<1$, it follows that $\hat{I}_{R}<0$ and $I^{*}_{SU}<0$. Thus, when $R_{C} < 1$, the reaction model (3) has a unique disease-free equilibrium $E^{0}$. When $R_{RC}>1$, it follows that the boundary equilibrium $\hat{E}$ exists. When $R_{RC} < R_{SC}$ and $R_{SC}>1$, the interior (positive) equilibrium $E^{*}$ exists. No matter how $R_{SC}$ and $R_{RC}$ are valued, the disease-free equilibrium $E^{0}$ always exists. The proof is completed. $\square$

In Table 1, we present a diagram to clearly show the relationship between the existence of equilibria and the values of the parameters $R_{SC}$, $R_{RC}$ and $R_{C}$.

Table 1 Existence of equilibria on the values of $R_{SC}$, $R_{RC}$ and $R_{C}$

4 Semi-, Strong and Persistent Traveling Waves for the Diffusive Model

Traveling wave is one of the elementary notions in the study of reaction–diffusion systems, the existence of which determines the long-term behavior of other solutions of the systems (Ruan and Xiao 2004; Weng and Zhao 2006; Huang 2016; Zhang 2017). In epidemiology, the existence and nonexistence of nontrivial traveling waves indicate whether an infectious disease could persist as a wave front of infection that travels geographically across vast distances. Therefore, the study of traveling waves is of great significance to the prevention and control of influenza.

More specifically, we consider a solution $(S(x,t), I_{SU}(x,t), I_{ST}(x,t), I_{R}(x,t))$ of the diffusive model (2), with the following form

$$\begin{aligned} S(x,t)=S(\xi ),\quad I_{i}(x,t)=I_{i}(\xi ),\quad \xi =x+ct, \end{aligned}$$

(12)

where $i = SU, ST, R$, and $c>0$ is the wave speed. A solution having the form (12) is called a traveling wave solution (or referred to as traveling wave) if $S(\xi )$ and $I_{i}(\xi ),\,i = SU, ST, R$, are defined for all $\xi \in {\mathbf {R}}$ and are nonnegative functions.

For the convenience of discussion below, we first give several definitions of different kinds of traveling waves as follows (Huang 2016; Zhang et al. 2016; Ai et al. 2017).

Definition 4.1

(Huang 2016; Zhang et al. 2016) A traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is called a semi-traveling wave connected to the disease-free equilibrium $E^{0}$ (for convenience, here we still use the same notation $E^{0}$ to represent the equilibrium of system (2)) if it satisfies the boundary condition

$$\begin{aligned} \lim _{\xi \rightarrow -\infty }(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))=E^{0}(S^{0},0,0,0). \end{aligned}$$

(13)

Definition 4.2

(Ai et al. 2017) A traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is strong if it satisfies

$$\begin{aligned} \begin{array}{l} (S(-\infty ), I_{SU}(-\infty ), I_{ST}(-\infty ), I_{R}(-\infty ))=E^{0}, \\ (S(+\infty ), I_{SU}(+\infty ), I_{ST}(+\infty ), I_{R}(+\infty ))=\hat{E}/E^{*}, \end{array} \end{aligned}$$

where $U(\pm \infty )=\lim _{\xi \rightarrow \pm \infty }U(\xi )$.

Definition 4.3

(Ai et al. 2017) A traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is persistent if there exist two positive constants $M_{1}$ and $M_{2}$ such that

$$\begin{aligned} \begin{array}{l} (S(-\infty ), I_{SU}(-\infty ), I_{ST}(-\infty ), I_{R}(-\infty ))=E^{0}, \\ M_{1}<\displaystyle \liminf _{\xi \rightarrow +\infty }S(\xi ),\quad \limsup _{\xi \rightarrow +\infty }S(\xi )<M_{2}, \\ M_{1}<\displaystyle \liminf _{\xi \rightarrow +\infty }I_{i}(\xi ),\quad \limsup _{\xi \rightarrow +\infty }I_{i}(\xi )<M_{2},\quad i = SU, ST, R. \end{array} \end{aligned}$$

Next we discuss the conditions for the existence of three kinds of traveling waves starting from the disease-free equilibrium $E^{0}$, i.e., semi-traveling waves, strong traveling waves and persistent traveling waves.

4.1 Semi-traveling Waves

In this subsection, to prove the existence of semi-traveling waves for the diffusive model (2), we first introduce an auxiliary system, the technique of which has been widely used (see Zhang and Wang 2014; Zhang 2017; Zhang et al. 2016; Ma 2007). Then, by linearizing the wave equations of the diffusive model (2) at disease-free equilibrium $E^{0}$, we construct a pair of upper–lower solutions for the auxiliary system. Finally, we use Schauder’s fixed-point theorem to establish the existence of semi-traveling waves for the auxiliary system. The detailed proof process is shown in Appendix A.

Now we state our main results about the auxiliary system as follows.

Lemma 4.4

If $R_{C}>1$, then there exists $c^{*}>0$ , defined by Lemma A.1, such that for any $c>c^{*}$, the auxiliary system (35) admits a nonnegative bounded semi-traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ satisfying the asymptotic boundary condition (13).

Proof

We conclude that there exists a fixed point of the operator G, denoted by $\mathrm{Sol} =(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))\in \mathfrak {L}$, by Schauder’s fixed-point theorem and Lemmas A.6, A.7 and A.8, which is equivalent to say that Sol is a nonnegative bounded traveling wave of the auxiliary system (35).

We can further show that Sol satisfies the asymptotic boundary condition (13). It is easy to see that $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))\rightarrow E^{0}(S^{0},0,0,0)$ when $\xi \rightarrow -\infty$ due to the definition of upper–lower solutions in (39) and Lemmas A.3, A.4 and A.5. So, the nonnegative bounded traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is a semi-traveling wave satisfying the asymptotic boundary condition (13). The proof is completed. $\square$

Based on Lemma 4.4, we give the conditions for the existence of semi-traveling waves for the diffusive model (2).

Theorem 4.5

If $R_{C}>1$, then there exists $c^{*}>0$ (defined by Lemma A.1) such that for any $c>c^{*}$, the diffusive model (2) admits a positive semi-traveling wave $(S(\xi ), I_{SU}(\xi )$, $I_{ST}(\xi )$, $I_{R}(\xi ))$ satisfying the asymptotic boundary condition (13) and $S(\xi )<S^{0}$ for any $\xi \in {\mathbf {R}}$. Furthermore,

$$\begin{aligned} \lim _{\xi \rightarrow -\infty }I_{i}(\xi )e^{-\lambda _{c}\xi }=\kappa _{i},\quad \lim _{\xi \rightarrow -\infty }I'_{i}(\xi )e^{-\lambda _{c}\xi }=\lambda _{c}\kappa _{i},\quad i=SU, ST, R, \end{aligned}$$

(14)

where $\kappa _{SU}=\kappa _{2}, \kappa _{ST}=\kappa _{3}, \kappa _{R}=\kappa _{4}$.

Proof

Set $\varUpsilon = \varUpsilon _{n} := \frac{1}{n}$. Obviously, the sequence $\{\varUpsilon _{n}\}$ satisfies $0<\varUpsilon _{i+1}<\varUpsilon _{i}<1$ and $\varUpsilon _{n}\rightarrow 0$ as $n\rightarrow +\infty$. By Lemma 4.4, there is a nonnegative semi-traveling wave

$$\begin{aligned} \varPhi _{n}(\xi )=(\varphi _{1n}(\xi ), \varphi _{2n}(\xi ), \varphi _{3n}(\xi ), \varphi _{4n}(\xi ))\in \mathfrak {L} \end{aligned}$$

of the auxiliary system (35) with $\varUpsilon = \varUpsilon _{n}$ satisfying the asymptotic boundary condition

$$\begin{aligned} (\varphi _{1n}(-\infty ), \varphi _{2n}(-\infty ), \varphi _{3n}(-\infty ), \varphi _{4n}(-\infty ))= E^{0}(S^{0},0,0,0). \end{aligned}$$

From the proof of Lemma A.8, we know that $\{|\varphi '_{in}(\xi )|\}$ are uniformly bounded for $i=1,2,3,4$ since $\varPhi _{n}(\xi )\in \mathfrak {L}$ is a fixed point of the operator G. In addition, $\{|\varphi ''_{in}(\xi )|\}$ and $\{|\varphi '''_{in}(\xi )|\}$ are also uniformly bounded since $\varPhi _{n}(\xi )$ is the solution of the auxiliary system (35) with $\varUpsilon = \varUpsilon _{n}$. Therefore, $\{\varPhi _{n}(\xi )\}, \{\varPhi '_{n}(\xi )\}, \{\varPhi ''_{n}(\xi )\}$ are equicontinuous and uniformly bounded in ${\mathbf {R}}$. Then, Arzelà–Ascoli theorem implies that there exists a subsequence $\{\varUpsilon _{n_{k}}\}$ such that $\varPhi _{n_{k}}(\xi )\rightarrow \varPsi (\xi ), \varPhi '_{n_{k}}(\xi )\rightarrow \varPsi '(\xi ), \varPhi ''_{n_{k}}(\xi )\rightarrow \varPsi ''(\xi )$ uniformly in any bounded closed interval when $k\rightarrow +\infty$, and pointwise on ${\mathbf {R}}$, where $\varPsi (\xi )=(\psi _{1}(\xi ), \psi _{2}(\xi ), \psi _{3}(\xi ), \psi _{4}(\xi ))$.

Since $\varPhi _{n_{k}}(\xi )$ is the solution of the auxiliary system (35), and let $\varUpsilon _{n_{k}}\rightarrow 0$, we obtain

$$\begin{aligned} \left\{ \begin{array}{ll} c\psi '_{1} = d_{S}\psi ''_{1}+\varLambda -\mu \psi _{1}-[\beta _{S}(\psi _{2}+\delta \psi _{3})+\beta _{R}\psi _{4}]\psi _{1}, \\ c\psi '_{2} = d_{SU}\psi ''_{2}+(1-f)\beta _{S}(\psi _{2}+\delta \psi _{3})\psi _{1}-(k_{U}+\mu )\psi _{2}, \\ c\psi '_{3} = d_{ST}\psi ''_{3}+f(1-r)\beta _{S}(\psi _{2}+\delta \psi _{3})\psi _{1}-(k_{T}+\mu )\psi _{3}, \\ c\psi '_{4} = d_{R}\psi ''_{4}+[fr\beta _{S}(\psi _{2}+\delta \psi _{3})+\beta _{R}\psi _{4}]\psi _{1}-(k_{R}+\mu )\psi _{4}. \end{array}\right. \end{aligned}$$

Therefore, $\varPsi (\xi )$ is a nonnegative semi-traveling wave of the diffusive model (2) satisfying the asymptotic boundary condition (13).

Next, we show that $\varPsi (\xi )$ is a positive semi-traveling wave of the diffusive model (2), i.e., $\psi _{i}(\xi )>0,\,i=S, SU, ST, R$ for any $\xi \in {\mathbf {R}}$.

Suppose that $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))\in \mathfrak {L}$ is a nonnegative semi-traveling wave of the diffusive model (2). For fixed $c>c^{*}$ and $\varUpsilon \in (0,1]$, then $\xi _{1}$, $\xi _{2}$ and $\xi _{3}$ defined in Lemmas A.3, A.4 and A.5 can be chosen such that they do not depend on the choice of $\varUpsilon$. So, by the definition of the profile set $\mathfrak {L}$ in (44), we know that there exists a constant $\xi _{0}\le \xi _{2}$ such that $S(\xi )>0$ for any $\xi <\xi _{0}$. Now we show that $S(\xi )>0$ for any $\xi \in {\mathbf {R}}$. On the contrary, we suppose that there exists $\xi ^{*}$ such that $S(\xi ^{*})=0$. Since $S(\xi )\ge 0$ for any $\xi \in {\mathbf {R}}$, $S(\xi ^{*})$ is a minimum, implying that $S'(\xi ^{*})=0$ and $S''(\xi ^{*})\ge 0$. Employing the first equation of system (36) yields $d_{S}S''(\xi ^{*})+\varLambda =0$, which is a contradiction. Thus, we have $S(\xi )>0$ for any $\xi \in {\mathbf {R}}$.

We then claim that $I_{SU}(\xi )>0$ for any $\xi \in {\mathbf {R}}$. In fact, there exists $\widetilde{\xi }_{0}\le \xi _{3}$ such that $I_{SU}(\xi )>0$ when $\xi <\widetilde{\xi }_{0}$. If there exists $\widetilde{\xi }^{*}$ such that $I_{SU}(\widetilde{\xi }^{*})=0$, then there exist constants $a_{1}, a_{2}$ such that $a_{1}<\xi _{3}<a_{2}$ and $\widetilde{\xi }^{*}\in (a_{1}, a_{2})$. It implies that $I_{SU}(\xi )$ achieves its minimum in $(a_{1}, a_{2})$ for any $\xi \in [a_{1}, a_{2}]$. From the second equation of system (36), we know that $I_{SU}(\xi )$ satisfies, for any $\xi \in [a_{1}, a_{2}],$

$$\begin{aligned} -d_{SU}I''_{SU}(\xi )+cI'_{SU}(\xi )+(k_{U}+\mu )I_{SU}(\xi ) = (1-f)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S(\xi )\ge 0. \end{aligned}$$

By the elliptic strong maximum principle [see Theorem 3.3.6 in Gilbarg and Trudinger 2001], it follows that $I_{SU}(\xi )$ $\equiv 0$ for $\xi \in [a_{1}, a_{2}]$. On the other hand, by Lemma A.3, we have $I_{SU}(\xi )>0$ for $\xi \in [a_{1}, \xi _{3})$, a contradiction. Similarly, by the elliptic strong maximum principle, it can be shown $I_{i}(\xi )>0,\,i=ST, R$ for any $\xi \in {\mathbf {R}}$.

Based on the above arguments, we easily obtain $S(\xi )<S^{0}$ for any $\xi \in {\mathbf {R}}$. Otherwise, there exists $\widehat{\xi }^{*}$ such that

$$\begin{aligned} d_{S}S''(\widehat{\xi }^{*})=[\beta _{S}(I_{SU}(\widehat{\xi }^{*})+\delta I_{ST}(\widehat{\xi }^{*})) +\beta _{R}I_{R}(\widehat{\xi }^{*})]S(\widehat{\xi }^{*})>0, \end{aligned}$$

a contradiction due to $S''(\widehat{\xi }^{*})\le 0$.

We finally show that the positive semi-traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ of the diffusive model (2) satisfies (14).

Let $(S_{n}(\xi ), I_{SUn}(\xi ), I_{STn}(\xi ), I_{Rn}(\xi ))\in \mathfrak {L}$ be a nonnegative semi-traveling wave of the diffusive model (35) with $\varUpsilon =\varUpsilon _{n}$ in Lemma 4.4. Let $\kappa _{SU}=\kappa _{2}, \kappa _{ST}=\kappa _{3}, \kappa _{R}=\kappa _{4}$. Since the selection of $\kappa _{i}, i=2,3,4$ is independent on $\varUpsilon$, by the definition of upper–lower solutions of the diffusive model (35), we have

$$\begin{aligned} \kappa _{j}e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi })\le \underline{I}_{jn}(\xi )\le I_{jn}(\xi )\le \bar{I}_{jn}(\xi )\le \kappa _{j}e^{\lambda _{c}\xi }, \end{aligned}$$

which follows that $\lim _{\xi \rightarrow -\infty }I_{jn}(\xi )e^{-\lambda _{c}\xi }=\kappa _{j},\;j=SU, ST, R.$

In addition, note that $(S_{n}(\xi ), I_{SUn}(\xi ), I_{STn}(\xi ), I_{Rn}(\xi ))\in \mathfrak {L}$ is a fixed point of the operator $G_{n}$. Applying L’Höspital rule to the maps $G_{in},\,i=S, SU, ST, R$, it is easy to see that $S'_{n}(-\infty )=0$ and $I'_{jn}(-\infty )=0,\,j=SU, ST, R$. Integrating both sides of the second equation of the diffusive model (35) from $-\infty$ to $\xi$ gives

$$\begin{aligned} d_{SU}I'_{SUn}(\xi )&= cI_{SUn}(\xi )-(1-f)\beta _{S}\int _{-\infty }^{\xi }(I_{SUn}(s)+\delta I_{STn}(s))S_{n}(s)\mathrm{d}s \\&\quad +(k_{U}+\mu )\int _{-\infty }^{\xi }I_{SUn}(s)\mathrm{d}s+\varUpsilon _{n}\int _{-\infty }^{\xi }I^{2}_{SUn}(s)\mathrm{d}s. \end{aligned}$$

Recall that $S_{n}(-\infty )=S^{0}$, $S'_{n}(-\infty )=0$, $I_{jn}(-\infty )=0$, $I'_{jn}(-\infty )=0$ and

$$\begin{aligned} \lim _{\xi \rightarrow -\infty }I_{jn}(\xi )e^{-\lambda _{c}\xi }=\kappa _{j},\quad j=SU, ST, R, \end{aligned}$$

then we have

$$\begin{aligned}&\lim _{\xi \rightarrow -\infty }I'_{SUn}(\xi )e^{-\lambda _{c}\xi } \\&\quad ={\lim _{\xi \rightarrow -\infty }}\frac{1}{d_{SU}}\left[ ce^{-\lambda _{c}\xi }I_{SUn}(\xi )-(1-f)\beta _{S}e^{-\lambda _{c}\xi }\int _{-\infty }^{\xi }(I_{SUn}(s)+\delta I_{STn}(s))S_{n}(s)\mathrm{d}s\right] \\&\qquad +\lim _{\xi \rightarrow -\infty }\frac{1}{d_{SU}}\left[ (k_{U}+\mu )e^{-\lambda _{c}\xi }\int _{-\infty }^{\xi }I_{SUn}(s)\mathrm{d}s+\varUpsilon _{n} e^{-\lambda _{c}\xi }\int _{-\infty }^{\xi }I^{2}_{SUn}(s)\mathrm{d}s\right] \\&\quad =\frac{c\lambda _{c}\kappa _{SU}-(1-f)\beta _{S}(\kappa _{SU}+\delta \kappa _{ST})S^{0}+(k_{U}+\mu )\kappa _{SU}}{d_{SU}\lambda _{c}}. \end{aligned}$$

By the first equation of the eigenvalue Eq. (38), we know

$$\begin{aligned} \frac{c\lambda _{c}\kappa _{SU}-(1-f)\beta _{S}(\kappa _{SU}+\delta \kappa _{ST})S^{0}+(k_{U}+\mu )\kappa _{SU}}{d_{SU}\lambda _{c}}=\lambda _{c}\kappa _{SU}. \end{aligned}$$

So, $\lim _{\xi \rightarrow -\infty }I'_{SUn}(\xi )e^{-\lambda _{c}\xi }=\lambda _{c}\kappa _{SU}$.

Based on the previous discussion in this lemma, we suppose that there exists a subsequence $\{n_{k}\}$ such that

$$\begin{aligned} S_{n_{k}}(\xi )\rightarrow S(\xi ), I_{jn_{k}}(\xi )\rightarrow I_{j}(\xi ),\quad j=SU, ST, R, \end{aligned}$$

here $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is a positive semi-traveling wave of diffusive model (2) satisfying the asymptotic boundary condition (13). Applying the limiting arguments yields

$$\begin{aligned} \lim _{\xi \rightarrow -\infty }I'_{SU}(\xi )e^{-\lambda _{c}\xi }=\lim _{k\rightarrow +\infty }\lim _{\xi \rightarrow -\infty }I'_{SUn_{k}}(\xi )e^{-\lambda _{c}\xi }=\lambda _{c}\kappa _{SU}. \end{aligned}$$

Similarly, we can also demonstrate $\lim _{\xi \rightarrow -\infty }I'_{j}(\xi )e^{-\lambda _{c}\xi }=\lambda _{c}\kappa _{j},~j=ST, R$. This completes the proof of the theorem. $\square$

In Theorem 4.5, we establish the existence of positive semi-traveling waves starting from the disease-free equilibrium $E^{0}$ for the diffusive model (2), where the disease-free equilibrium $E^{0}$ is the population state before the transmission of influenza. Meanwhile, its presence means that the influenza will spread among the crowd. Different from reaction model (3), the control reproduction number $R_{C}$ is not the only factor that determines whether influenza spreads in space. If influenza spreads among population, except for $R_{C}>1$, the wave speed c should be greater than the critical wave speed $c^{*}$, which depends on the diffusion coefficients of three infected subclasses. This implies that the speed of group movement affects the likelihood of a global influenza outbreak. In terms of influenza control, it can reduce the scale of influenza outbreak by restricting individual travel and implementing home quarantine. Equation (14) gives the growth rates of different infection strains in the initial stage, which is favorable for us to make reasonable predictions and rationally arrange medical resources.

4.2 Strong Traveling Waves

By Theorem 4.5, we have obtained the conditions that positive semi-traveling waves exist. In this subsection, we will further study under what conditions the final state of semi-traveling waves will tend to the boundary equilibrium $\hat{E}(\hat{S},0,0,\hat{I}_{R})$.

Theorem 4.6

Under the condition of $R_{C}>1$, if $R_{SU}\le R_{R}$ and $R_{ST}\le R_{R}$ (defined in (6)), then for any $c>c^{*}$ ($c^{*}>0$ is defined by Lemma A.1), the diffusive model (2) has a strong traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ connecting $E^{0}(S^{0},0,0,0)$ and $\hat{E}(\hat{S},0,0,\hat{I}_{R})$.

Proof

From Theorem 4.5, we know that when $R_{C}>1$, there exists $c^{*}>0$ such that for any $c>c^{*}$, the diffusive model (2) admits a positive semi-traveling wave $(S(\xi ), I_{SU}(\xi )$, $I_{ST}(\xi )$, $I_{R}(\xi ))$ satisfying

$$\begin{aligned} (S(-\infty ), I_{SU}(-\infty ), I_{ST}(-\infty ), I_{R}(-\infty ))=E^{0}(S^{0},0,0,0) \end{aligned}$$

with $S(\xi )<S^{0}$ for any $\xi \in {\mathbf {R}}$.

To complete the proof, it is sufficient to show

$$\begin{aligned} (S(+\infty ), I_{SU}(+\infty ), I_{ST}(+\infty ), I_{R}(+\infty ))=\hat{E}(\hat{S},0,0,\hat{I}_{R}). \end{aligned}$$

We first claim that $\frac{S'(\xi )}{S(\xi )}$ and $\frac{I'_{j}(\xi )}{I_{j}(\xi )},~j=SU, ST, R$ are bounded for any $\xi \in {\mathbf {R}}$. To get the result, we rewrite wave Eq.  (36) of the diffusive model (2) as follows

$$\begin{aligned}&\left( \begin{array}{cccc} d_{S} &{} 0 &{} 0 &{} 0 \\ 0 &{} d_{SU} &{} 0 &{} 0 \\ 0 &{} 0 &{} d_{ST} &{} 0 \\ 0 &{} 0 &{} 0 &{} d_{R} \\ \end{array} \right) \begin{pmatrix} S'' \\ I''_{SU} \\ I''_{ST} \\ I''_{R} \end{pmatrix}-c\begin{pmatrix} S' \\ I'_{SU} \\ I'_{ST} \\ I'_{R} \end{pmatrix} \nonumber \\&\quad +\left( \begin{array}{cccc} b_{11}(\xi ) &{} 0 &{} 0 &{} 0 \\ b_{21}(\xi ) &{} b_{22}(\xi ) &{} 0 &{} 0 \\ b_{31}(\xi ) &{} 0 &{} b_{33}(\xi ) &{} 0 \\ b_{41}(\xi ) &{} 0 &{} 0 &{} b_{44}(\xi ) \\ \end{array} \right) \begin{pmatrix} S \\ I_{SU} \\ I_{ST} \\ I_{R} \end{pmatrix}=0, \end{aligned}$$

(15)

where

$$\begin{aligned} b_{11}(\xi )&=\frac{\varLambda }{S(\xi )}-\mu -[\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )], \\ b_{21}(\xi )&=(1-f)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi )),\quad b_{22}(\xi )=-(k_{U}+\mu ), \\ b_{31}(\xi )&=f(1-r)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi )),\quad b_{33}(\xi )=-(k_{T}+\mu ), \\ b_{41}(\xi )&=fr\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi ),\quad b_{44}(\xi )=-(k_{R}+\mu ). \end{aligned}$$

By Lemmas A.3, A.4 and A.5, it is not difficult to see that the functions $b_{k1}(\xi ), b_{kk}(\xi )$, for $k=1,2,3,4$ are bounded. Moreover, $b_{k1}(\xi )>0$, for $k=2,3,4$ due to the fact $S(\xi )>0$ and $I_{j}(\xi )>0,~j=SU, ST, R$ for any $\xi \in {\mathbf {R}}$. We can apply Harnack inequality (see Theorem 1.1 in Chen and Zhao 1997) for system (15), and it follows that there exists a constant $D>0$ such that for any $\xi \in {\mathbf {R}}$, we have

$$\begin{aligned}&\max _{[s-1,s+1]}S(\xi )\le D\min _{[s-1,s+1]}S(\xi ), \\&\max _{[s-1,s+1]}I_{j}(\xi )\le D\min _{[s-1,s+1]}I_{j}(\xi ),\quad j=SU, ST, R, \end{aligned}$$

where D depends only on the coefficients of system (15) and the length of interval $[s-1,s+1]$. As a consequence, we can deduce that there exists some constant $D_{1}>0$ such that

$$\begin{aligned} \left| \frac{S'(\xi )}{S(\xi )}\right| +\sum _{j=SU, ST, R}\left| \frac{I'_{j}(\xi )}{I_{j}(\xi )}\right| \le D_{1},\quad \xi \in {\mathbf {R}}. \end{aligned}$$

Set $V_{S}(\xi )=S'(\xi ), V_{j}(\xi )= I'_{j}(\xi ),~j=SU, ST, R$, the wave Eq.  (36) of the diffusive model (2) can be transformed into the following equivalent system

$$\begin{aligned} \left\{ \begin{array}{ll} S' = V_{S}, \\ d_{S}V'_{S} = cV_{S}-\varLambda +\mu S+[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ I'_{SU} = V_{SU}, \\ d_{SU}V'_{SU} = cV_{SU}-(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S+(k_{U}+\mu )I_{SU}, \\ I'_{ST} = V_{ST}, \\ d_{ST}V'_{ST} = cV_{ST}-f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S+(k_{T}+\mu )I_{ST}, \\ I'_{R} = V_{R}, \\ d_{R}V'_{R} = cV_{R}-[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S+(k_{R}+\mu )I_{R}. \end{array}\right. \end{aligned}$$

(16)

Finally, we complete the proof of the lemma by introducing a Lyapunov functional, determining that the positive semi-traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ of the diffusive model (2) converges to the boundary equilibrium $\hat{E}(\hat{S},0,0,\hat{I}_{R})$ as $\xi \rightarrow +\infty$. Equivalently, it corresponds to the convergence of the solution

$$\begin{aligned} (S(\xi ), V_{S}(\xi ), I_{SU}(\xi ), V_{SU}(\xi ), I_{ST}(\xi ), V_{ST}(\xi ), I_{R}(\xi ), V_{R}(\xi )) \end{aligned}$$

of system (16) to $\hat{E}(\hat{S},0,0,0,0,0,\hat{I}_{R},0).$ [For the convenience, we still use the same notation $\hat{E}$ to denote the equilibrium of system (16).] To this end, we consider the following Lyapunov functional

$$\begin{aligned} L(\xi ):=L_{S}(\xi )+L_{SU}(\xi )+L_{ST}(\xi )+L_{R}(\xi ), \end{aligned}$$

where

$$\begin{aligned}&L_{S}(\xi )= cS-d_{S}V_{S}+\frac{\hat{S}d_{S}V_{S}}{S}-c\int _{\hat{S}}^{S}\frac{\hat{S}}{\eta }\mathrm{d}\eta , \\&L_{SU}(\xi )= cI_{SU}-d_{SU}V_{SU}, \\&L_{ST}(\xi )= cI_{ST}-d_{ST}V_{ST}, \\&L_{R}(\xi )= cI_{R}-d_{R}V_{R}+\frac{\hat{I}_{R}d_{R}V_{R}}{I_{R}}-c\int _{\hat{I}_{R}}^{I_{R}}\frac{\hat{I}_{R}}{\eta }\mathrm{d}\eta . \end{aligned}$$

Then, through a simple calculation, the derivative of $L_{S}(\xi )$ along the solution of system (16) satisfies

$$\begin{aligned} \frac{\mathrm{d}L_{S}(\xi )}{\mathrm{d}\xi }&=cV_{S}(\xi ) -d_{S}V'_{S}(\xi )+\frac{d_{S}\hat{S}(V'_{S}(\xi )S(\xi )-V_{S}(\xi )S'(\xi ))}{S^{2}(\xi )}-c\hat{S}\frac{\hat{S}}{S(\xi )} \\&=[cV_{S}(\xi ) -d_{S}V'_{S}(\xi )]\frac{S(\xi )-\hat{S}}{S(\xi )}-\frac{d_{S}\hat{S}V^{2}_{S}(\xi )}{S^{2}(\xi )} \\&\le [cV_{S}(\xi )-d_{S}V'_{S}(\xi )]\frac{S(\xi )-\hat{S}}{S(\xi )}. \end{aligned}$$

Similarly, we can calculate

$$\begin{aligned} \frac{\mathrm{d}L_{SU}(\xi )}{\mathrm{d}\xi }=cV_{SU}(\xi )-d_{SU}V'_{SU}(\xi ), \quad \frac{\mathrm{d}L_{ST}(\xi )}{\mathrm{d}\xi }=cV_{ST}(\xi )-d_{ST}V'_{ST}(\xi ), \end{aligned}$$

and $\frac{\mathrm{d}L_{R}(\xi )}{\mathrm{d}\xi }\le [cV_{R}(\xi )-d_{R}V'_{R}(\xi )]\frac{I_{R}(\xi )-\hat{I}_{R}}{I_{R}(\xi )}.$ Therefore, we have

$$\begin{aligned} \frac{\mathrm{d}L(\xi )}{\mathrm{d}\xi }&=\frac{L_{S}(\xi )}{\mathrm{d}\xi }+\frac{L_{SU}(\xi )}{\mathrm{d}\xi }+\frac{L_{ST}(\xi )}{\mathrm{d}\xi }+\frac{L_{R}(\xi )}{\mathrm{d}\xi } \\&\le [cV_{S}(\xi )-d_{S}V'_{S}(\xi )]\frac{S(\xi )-\hat{S}}{S(\xi )}+[cV_{SU}(\xi )-d_{SU}V'_{SU}(\xi )] \\&\quad +[cV_{ST}(\xi )-d_{ST}V'_{ST}(\xi )]+[cV_{R}(\xi )-d_{R}V'_{R}(\xi )]\frac{I_{R}(\xi )-\hat{I}_{R}}{I_{R}(\xi )}. \end{aligned}$$

By system (16), we can further get

$$\begin{aligned}&\frac{\mathrm{d}L(\xi )}{\mathrm{d}\xi } \\&\quad \le \left\{ \varLambda -\mu S(\xi )-[\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )]S(\xi )\right\} \frac{S(\xi )-\hat{S}}{S(\xi )} \\&\qquad +\left[ (1-f)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S(\xi )-(k_{U}+\mu )I_{SU}(\xi )\right] \\&\qquad +\left[ f(1-r)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S(\xi )-(k_{T}+\mu )I_{ST}(\xi )\right] \\&\qquad +\left\{ [fr\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )]S(\xi )-(k_{R}+\mu )I_{R}(\xi )\right\} \frac{I_{R}(\xi )-\hat{I}_{R}}{I_{R}(\xi )}. \end{aligned}$$

Together with the following equilibrium conditions $\varLambda =\mu \hat{S}+\beta _{R}\hat{S}\hat{I}_{R}$ and $k_{R}+\mu =\beta _{R}\hat{S},$ we have

$$\begin{aligned} \frac{\mathrm{d}L(\xi )}{\mathrm{d}\xi }&\le \left\{ \mu \hat{S}+\beta _{R}\hat{S}\hat{I}_{R}-\mu S(\xi )-\left[ \beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )\right] S(\xi )\right\} \frac{S(\xi )-\hat{S}}{S(\xi )} \\&\qquad +\left[ (1-f)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S(\xi )-(k_{U}+\mu )I_{SU}(\xi )\right] \\&\qquad +\left[ f(1-r)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S(\xi )-(k_{T}+\mu )I_{ST}(\xi )\right] \\&\qquad +\left\{ \left[ fr\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )\right] S(\xi )-\beta _{R}\hat{S}I_{R}(\xi )\right\} \frac{I_{R}(\xi )-\hat{I}_{R}}{I_{R}(\xi )} \\&\quad =-\mu \frac{(S(\xi )-\hat{S})^{2}}{S(\xi )}+\beta _{R}\hat{S}\hat{I}_{R}\left( 2-\frac{\hat{S}}{S(\xi )}-\frac{S(\xi )}{\hat{S}}\right) \\&\qquad +\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))\hat{S}-(k_{U}+\mu )I_{SU}(\xi )-(k_{T}+\mu )I_{ST}(\xi ) \\&\qquad -\frac{fr\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S(\xi )\hat{I}_{R}}{I_{R}(\xi )} \\&\quad \le \beta _{R}\hat{S}\hat{I}_{R}\left( 2-\frac{\hat{S}}{S(\xi )}-\frac{S(\xi )}{\hat{S}}\right) \\&\qquad +(k_{U}+\mu )I_{SU}(\xi )\left( \frac{\beta _{S}\hat{S}}{k_{U}+\mu }-1\right) +(k_{T}+\mu )I_{ST}(\xi )\left( \frac{\beta _{S}\delta \hat{S}}{k_{T}+\mu }-1\right) . \end{aligned}$$

Let $\varTheta (x):=1-x+\ln x$, for $x\in (0,+\infty )$. Using the fact $\hat{S}=\frac{S^{0}}{R_{RC}}=\frac{1}{R_{R}}$ and the property that $\varTheta (x)\le 0$ with $\varTheta (x)=0$ if and only if $x=1$ gives

$$\begin{aligned} \frac{\mathrm{d}L(\xi )}{\mathrm{d}\xi }&\le \beta _{R}\hat{S}\hat{I}_{R}\left[ \varTheta \left( \frac{\hat{S}}{S(\xi )}\right) +\varTheta \left( \frac{S(\xi )}{\hat{S}}\right) \right] \\&\quad +(k_{U}+\mu )I_{SU}(\xi )\left( \frac{R_{SU}}{R_{R}}-1\right) +(k_{T}+\mu )I_{ST}(\xi )\left( \frac{R_{ST}}{R_{R}}-1\right) \\&\le (k_{U}+\mu )I_{SU}(\xi )\left( \frac{R_{SU}}{R_{R}}-1\right) +(k_{T}+\mu )I_{ST}(\xi )\left( \frac{R_{ST}}{R_{R}}-1\right) . \end{aligned}$$

It is obvious that $\frac{\mathrm{d}L(\xi )}{\mathrm{d}\xi }\le 0$ holds for all $\xi \in {\mathbf {R}}$ when $R_{SU}\le R_{R}$ and $R_{ST}\le R_{R}$, implying that $L(\xi )$ is decreasing. Furthermore, $\frac{\mathrm{d}L(\xi )}{\mathrm{d}\xi }=0$ if and only if

$$\begin{aligned} (S, V_{S}, I_{SU}, V_{SU}, I_{ST}, V_{ST}, I_{R}, V_{R})=\hat{E}(\hat{S},0,0,0,0,0,\hat{I}_{R},0). \end{aligned}$$

Finally, LaSalle’s invariance principle (1976) implies

$$\begin{aligned} (S(\xi ), V_{S}(\xi ), I_{SU}(\xi ), V_{SU}(\xi ), I_{ST}(\xi ), V_{ST}(\xi ), I_{R}(\xi ), V_{R}(\xi ))\rightarrow \hat{E}(\hat{S},0,0,0,0,0,\hat{I}_{R},0) \end{aligned}$$

as $\xi \rightarrow +\infty$. That is, $(S(+\infty ), I_{SU}(+\infty ), I_{ST}(+\infty ), I_{R}(+\infty ))=\hat{E}(\hat{S},0,0,\hat{I}_{R})$. The proof of the theorem is completed. $\square$

In Theorem 4.6, we obtain the conditions for strong traveling waves connecting the disease-free equilibrium $E^{0}$ and boundary equilibrium $\hat{E}$. From $R_{SU}\le R_{R}$ and $R_{ST}\le R_{R}$, we can easily derive that $R_{SC}<R_{RC}$. So we address the connection problem between two equilibria $E^{0}$ and $\hat{E}$ in the later two cases of Table 1 in Sect. 3. The existence of this strong traveling wave shows that the spread of influenza is successful, which describes the influenza propagation into the susceptible individuals from an initial disease-free equilibrium to the final boundary equilibrium with only resistant strain. From $R_{SU}\le R_{R}$ and $R_{ST}\le R_{R}$, we see that it is unfavorable for the formation of sensitive strains in the competition of three strains, leading to the extinction of sensitive strains. In this case, according to the mathematical expression of $\hat{I}_{R}$, the resistant strains can be significantly reduced by improving the cure rate of drug-resistant individuals. In order to prevent the large-scale spread of resistant strains, we should reasonably restrict the flow of drug-resistant individuals.

4.3 Persistent Traveling Waves

We can easily show that the positive semi-traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ of the diffusive model (2) in Theorem 4.5 satisfies

$$\begin{aligned} (S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))\in \mathfrak {L}, \end{aligned}$$

which implies $\limsup _{\xi \rightarrow +\infty }S(\xi )\le S^{0},\,\,\limsup _{\xi \rightarrow +\infty }I_{i}(\xi )\le \kappa _{i}K^{*},\,\,i=SU, ST, R,$ where $\kappa _{SU}=\kappa _{2}, \kappa _{ST}=\kappa _{3}, \kappa _{R}=\kappa _{4}$.

To prove that the positive semi-traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is persistent, we only need to prove

$$\begin{aligned} \liminf _{\xi \rightarrow +\infty }S(\xi )>0,\quad \liminf _{\xi \rightarrow +\infty }I_{i}(\xi )>0,\quad i=SU, ST, R. \end{aligned}$$

For this, we will apply the uniform persistence Theorem 4.5 in Thieme (1993) and restate it as Lemma B.1. To use Lemma B.1, we define

$$\begin{aligned} X_{1}&=\{(S, V_{S}, I_{SU}, V_{SU}, I_{ST}, V_{ST}, I_{R}, V_{R}): (S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))~\text {is a} \\&\qquad \text {positive semi-traveling of the diffusive model\,(2) in Theorem\,4.5}\\&\qquad \text {and} V_{S}(\xi )=S'(\xi ), V_{j}(\xi )=I'_{j}(\xi ),\quad j=SU, ST, R\}, \\ X_{2}&=\{(S, V_{S}, 0, 0, 0, 0, I_{R}, V_{R}): 0\le S\le S^{0},\;|V_{S}|\le D_{1}|S|,\\&\qquad \qquad 0\le I_{R}\le \kappa _{4}K^{*},\;|V_{R}|\le D_{1}|I_{R}|\}, \end{aligned}$$

where $\kappa _{4}$ and $K^{*}$ have been determined in Lemmas A.1 and A.3 and $D_{1}$ is a positive constant that is just determined in Theorem 4.6.

By establishing Lemma B.2, we get the conclusion that $W^{s}(E^{0})\cap X_{1}=\emptyset$, which is to prepare for the proof of the following theorem.

Theorem 4.7

If $R_{SC}>1>R_{RC}$ [defined in (7) and (8)], and $c>\max \{c^{*}, \tilde{c}^{*}\}$ ($c^{*}>0$ is defined by Lemma A.1, $\tilde{c}^{*}$ is defined by Lemma B.2) hold. The diffusive model (2) admits a persistent traveling wave $(S(\xi ), I_{SU}(\xi )$, $I_{ST}(\xi )$, $I_{R}(\xi ))$ satisfying the asymptotic boundary condition (13).

Proof

Assume that, when $\xi _{i}\rightarrow +\infty$ (as $i\rightarrow +\infty$),

$$\begin{aligned}&(S(\xi _{i}), V_{S}(\xi _{i}), I_{SU}(\xi _{i}), V_{SU}(\xi _{i}), I_{ST}(\xi _{i}), V_{ST}(\xi _{i}), I_{R}(\xi _{i}), V_{R}(\xi _{i}))\\&\quad \longrightarrow (S^{*}, V^{*}_{S}, I^{*}_{SU}, V^{*}_{SU}, I^{*}_{ST}, V^{*}_{ST}, I^{*}_{R}, V^{*}_{R}). \end{aligned}$$

We first prove several results as follows:

• (a) $I^{*}_{SU}=0\Rightarrow V^{*}_{SU}=I^{*}_{ST}=V^{*}_{ST}=0$;

In view of the fact that $I^{*}_{SU}=0$ and $V_{SU}=I^{'}_{SU}$, if $V^{*}_{SU}\ne 0$, by the Taylor formula, we know there exists $\xi ^{*}$ such that $I_{SU}(\xi ^{*})<0$, a contradiction. In addition, we assume that $\lim _{\xi \rightarrow +\infty }I^{''}_{SU}(\xi )$ exists, then we can show that $\lim _{\xi \rightarrow +\infty }I^{''}_{SU}(\xi )\ge 0$. By selecting a subsequence of $\xi _{i}$, denoted by $\xi _{i_{j}}$, we directly give the Taylor expansion of $I_{SU}(\xi _{i_{j}})$ at $\xi ^{0}_{i_{j}}$:

$$\begin{aligned} I_{SU}(\xi _{i_{j}}) = I_{SU}(\xi ^{0}_{i_{j}})+I^{'}_{SU}(\xi ^{0}_{i_{j}})(\xi _{i_{j}}-\xi ^{0}_{i_{j}})+I^{''}_{SU}(\xi ^{0}_{i_{j}})(\xi _{i_{j}}-\xi ^{0}_{i_{j}})^{2}+o((\xi _{i_{j}}-\xi ^{0}_{i_{j}})^{2}). \end{aligned}$$

(17)

Let $\xi ^{0}_{i_{j}}\rightarrow +\infty$, implying that $I_{SU}(\xi ^{0}_{i_{j}})\rightarrow 0$ and $I^{'}_{SU}(\xi ^{0}_{i_{j}})\rightarrow 0$. Combining with $I_{SU}(\xi _{i_{j}})\ge 0$, we can get $\lim _{\xi \rightarrow +\infty }I^{''}_{SU}(\xi )\ge 0$ from (17).

Now go back to the equation of $I_{SU}$ in wave Eq. (36) of the diffusive model (2)

$$\begin{aligned} cI'_{SU}(\xi ) = d_{SU}I''_{SU}(\xi )+(1-f)\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))S-(k_{U}+\mu )I_{SU}(\xi ). \end{aligned}$$

(18)

Take the limit on both sides of equality (18), in order to make the limiting equation still hold, we have $I^{''}_{SU}(+\infty )=0$ and $I_{ST}(+\infty )=I^{*}_{ST}=0$. Similar to the proof of $V^{*}_{SU}=0$, we can show $V^{*}_{ST}=0$.

Through similar discussions, we can also prove the following results (b) and (c).

• (b) $I^{*}_{ST}=0\Rightarrow V^{*}_{ST}=I^{*}_{SU}=V^{*}_{SU}=0$;

• (c) $I^{*}_{R}=0\Rightarrow V^{*}_{R}=I^{*}_{SU}=V^{*}_{SU}=I^{*}_{ST}=V^{*}_{ST}=0$.

By (a), (b) and (c), we can find that $I^{*}_{SU}=0\Leftrightarrow I^{*}_{ST}=0$, $I^{*}_{R}=0\Rightarrow I^{*}_{SU}=I^{*}_{ST}=0$, while $I^{*}_{SU}=I^{*}_{ST}=0$ does not imply $I^{*}_{R}=0$. So we only need to show that $X_{2}$ excludes $X_{1}$, if we want to prove that $S(\xi ), I_{SU}(\xi ), I_{ST}(\xi )$ and $I_{R}(\xi )$ are persistent. Now we study the dynamics of system (16) in $X_{2}$. Equivalently, we consider the subsystem of system (16)

$$\begin{aligned} \left\{ \begin{array}{ll} S' = V_{S}, &{}\quad d_{S}V'_{S} = cV_{S}-\varLambda +\mu S+\beta _{R}I_{R}S, \\ I'_{R} = V_{R}, &{}\quad d_{R}V'_{R} = cV_{R}-\beta _{R}I_{R}S+(k_{R}+\mu )I_{R}. \end{array}\right. \end{aligned}$$

(19)

If $R_{RC}<1$, system (19) has a unique equilibrium $\bar{E}^{0}(S^{0},0,0,0)$. Now we consider the Jacobian matrix of (19) at $\bar{E}^{0}$, which has the form

$$\begin{aligned}\bar{J}=\left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ \frac{\mu }{d_{S}} &{} \frac{c}{d_{S}} &{} \frac{\beta _{R}S^{0}}{d_{S}} &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} \frac{k_{R}+\mu -\beta _{R}S^{0}}{d_{IR}} &{} \frac{c}{d_{IR}} \\ \end{array} \right) . \end{aligned}$$

The characteristic equation of $\bar{J}$ is $(d_{S}\lambda ^{2}-c\lambda -\mu )\left[ d_{R}\lambda ^{2}-c\lambda +\beta _{R}S^{0}-(k_{R}+\mu )\right] =0.$ It is easy to calculate the eigenvalues of $\bar{J}$ as follows:

$$\begin{aligned} \lambda ^{\pm }_{S}=\frac{c\pm \sqrt{c^{2}+4d_{S}\mu }}{2d_{S}},\quad \lambda ^{\pm }_{R}=\frac{c\pm \sqrt{c^{2}+4d_{R}(k_{R}+\mu )(1-R_{RC})}}{2d_{R}}. \end{aligned}$$

When $R_{RC}<1$ and $c>0$, the real part of all eigenvalues of $\bar{J}$ is nonzero, by the Hopf bifurcation theorem (Marsden and McCracken 1976), we know there is no periodic solution around $\bar{E}^{0}$. Obviously, there is no heteroclinic orbit connecting $\bar{E}^{0}$ for any $c>0$ as $R_{RC}<1$.

Finally, we need to rule out the possibility of a homoclinic connection at $\bar{E}^{0}$. For the non-degenerated critical point $\bar{E}^{0}$, if there is a homoclinic orbit l connecting $\bar{E}^{0}$, then we have $l\subseteq W^{U}(\bar{E}^{0})\cap W^{S}(\bar{E}^{0})$. The eigenvectors of matrix $\bar{J}$ corresponding to eigenvalues $\lambda ^{\pm }_{i}, i=S, R$ are

$$\begin{aligned} h^{+}_{S}&=(1, \lambda ^{+}_{S}, 0, 0)^T,\quad h^{+}_{R}=(\beta _{R}S^{0}, \lambda ^{+}_{R}\beta _{R}S^{0}, P_{S}(\lambda ^{+}_{R}), \lambda ^{+}_{R}P_{S}(\lambda ^{+}_{R}))^T, \\ h^{-}_{S}&=(1, \lambda ^{-}_{S}, 0, 0)^T,\quad h^{-}_{R}=(\beta _{R}S^{0}, \lambda ^{-}_{R}\beta _{R}S^{0}, P_{S}(\lambda ^{-}_{R}), \lambda ^{-}_{R}P_{S}(\lambda ^{-}_{R}))^T, \end{aligned}$$

where $P_{S}(\lambda )=d_{S}\lambda ^{2}-c\lambda -\mu$.

The unstable subspace of the linearized system of (19) at $\bar{E}^{0}$ is spanned by $h^{+}_{S}$ and $h^{+}_{R}$, and the stable subspace is spanned by $h^{-}_{S}$ and $h^{-}_{R}$. If there is a homoclinic connection at $\bar{E}^{0}$, then $l-\bar{E}^{0}\ne \emptyset$, we suppose that there is some point $P^{0}\in l-\bar{E}^{0}$ such that $P^{0}\in W^{U}(\bar{E}^{0})\cap W^{S}(\bar{E}^{0})$. Through simple calculations, together with $h^{+}_{S}h^{-}_{S}<0$ and $h^{+}_{R}h^{-}_{R}<0$, we can show $P^{0}=\bar{E}^{0}$, a contradiction. So there do not exist homoclinic orbits in $X_{2}$ for system (19).

The above discussions imply that the sets $\varOmega _{2}$ and M in Lemma B.1 are given by $\varOmega _{2}=E^{0}=M$. Obviously, M is an acyclic isolated covering of $\varOmega _{2}$. Applying Lemmas B.1 and B.2 completes the proof of the theorem. $\square$

In Theorem 4.7, we only give the existence of persistent traveling waves starting from the disease-free equilibrium since it is difficult to construct a Lyapunov functional or a pair of closed upper–lower solutions which converge to the positive equilibrium $E^{*}$ as $\xi \rightarrow +\infty$. Although we can determine the components of the final state of persistent traveling waves are positive, it does not mean the final state of persistent traveling waves is $E^{*}$. At the end of influenza spread, susceptible individuals and infected individuals with sensitive and resistant strains may coexist at constant levels ($E^{*}$) or periodically fluctuating state. However, Theorem 4.7 can still tell us the propagation speed of infection into susceptible individuals.

Biologically, it is indeed of public health importance, indicating that if few infectives are introduced into a completely susceptible population, then the infected individuals with sensitive and resistant strains would not vanish at the end of the wavefront. The condition $R_{SC}>1>R_{RC}$ implies that sensitive strains are more competitive than resistant strain. During the proof process, we find that two types of sensitive strains cannot disappear alone; moreover, the extinction of resistant strain must be accompanied by the extinction of sensitive strains.

5 Nonexistence of Semi-traveling Waves and Estimation of Minimal Wave Speed for the Diffusive Model

Now we show the nonexistence of semi-traveling waves for the diffusive model (2) in the following three cases: (I) $R_{C}<1$ and $c>0$; (II) $R_{RC}>1$, $R_{SC}\ne 1$ and $0<c<c_{1}^{*}$; and (III) $R_{SC}>1$, $R_{RC}\ne 1$ and $0<c<c_{2}^{*}$. In addition, we also give an estimation of minimal wave speed.

5.1 Nonexistence of Semi-traveling Waves

5.1.1 Case I: $R_{C}<1$ and $c>0$

Theorem 5.1

Suppose that $R_{C}<1$, then for any $c>0$, the diffusive model (2) has no nonnegative bounded semi-traveling waves (nontrivial) satisfying the asymptotic boundary condition (13). That is, in addition to the trivial semi-traveling wave, the diffusive model (2) does not admit any traveling wave connecting the disease-free steady state $E^{0}$ itself.

Proof

Suppose that the diffusive model (2) admits a nonnegative bounded semi-traveling wave (nontrivial) satisfying the asymptotic boundary condition (13). Without loss of generality, we assume that $0\le S(\xi )\le S^{0}$ and $I(\xi )\ge 0$ for $\xi \in {\mathbf {R}}$.

Note that the three equations for $(I_{SU}, I_{ST}, I_{R})$ in wave Eq. (36) of the diffusive model (2) can be transformed into

$$\begin{aligned} I_{SU}(\xi )&= \int _{-\infty }^{\xi }\frac{k_{U}+\mu }{\rho _{SU}}e^{\lambda ^{-}_{SU}(\xi -t)}\frac{1}{k_{U}+\mu }H_{SU}(t)\mathrm{d}t\nonumber \\&\quad +\int _{\xi }^{+\infty }\frac{k_{U}+\mu }{\rho _{SU}}e^{\lambda ^{+}_{SU}(\xi -t)}\frac{1}{k_{U}+\mu }H_{SU}(t)\mathrm{d}t, \nonumber \\ I_{ST}(\xi )&= \int _{-\infty }^{\xi }\frac{k_{T}+\mu }{\rho _{ST}}e^{\lambda ^{-}_{ST}(\xi -t)}\frac{1}{k_{T}+\mu }H_{ST}(t)\mathrm{d}t\nonumber \\&\quad +\int _{\xi }^{+\infty }\frac{k_{T}+\mu }{\rho _{ST}}e^{\lambda ^{+}_{ST}(\xi -t)}\frac{1}{k_{T}+\mu }H_{ST}(t)\mathrm{d}t, \nonumber \\ I_{R}(\xi )&= \int _{-\infty }^{\xi }\frac{k_{R}+\mu }{\rho _{R}}e^{\lambda ^{-}_{R}(\xi -t)}\frac{1}{k_{R}+\mu }H_{R}(t)\mathrm{d}t\nonumber \\&\quad +\int _{\xi }^{+\infty }\frac{k_{R}+\mu }{\rho _{R}}e^{\lambda ^{+}_{R}(\xi -t)}\frac{1}{k_{R}+\mu }H_{R}(t)\mathrm{d}t, \end{aligned}$$

(20)

where $\lambda ^{\pm }_{SU}=\frac{c\pm \sqrt{c^{2}+4d_{SU}(k_{U}+\mu )}}{2d_{SU}},\,\, \lambda ^{\pm }_{ST}=\frac{c\pm \sqrt{c^{2}+4d_{ST}(k_{T}+\mu )}}{2d_{ST}}$,

$$\begin{aligned}&\lambda ^{\pm }_{R}=\frac{c\pm \sqrt{c^{2}+4d_{R}(k_{R}+\mu )}}{2d_{R}},\quad \rho _{SU}=\lambda ^{+}_{SU}-\lambda ^{-}_{SU},\quad \rho _{ST}=\lambda ^{+}_{ST}-\lambda ^{-}_{ST},\\&\quad \rho _{R}=\lambda ^{+}_{R}-\lambda ^{-}_{R},\\&H_{SU}(t)=(1-f)\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))S(t),\\&H_{ST}(t)=f(1-r)\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))S(t),\\&H_{R}(t)=[fr\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))+\beta _{R}I_{R}(t)]S(t). \end{aligned}$$

According to (20) and assumptions, we have

$$\begin{aligned} I_{SU}(\xi )&\le \int _{-\infty }^{\xi }\frac{k_{U}+\mu }{\rho _{SU}}e^{\lambda ^{-}_{SU}(\xi -t)}\frac{1}{k_{U}+\mu }(1-f)\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))S^{0}\mathrm{d}t \nonumber \\&\quad +\int _{\xi }^{+\infty }\frac{k_{U}+\mu }{\rho _{SU}}e^{\lambda ^{+}_{SU}(\xi -t)}\frac{1}{k_{U}+\mu }(1-f)\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))S^{0}\mathrm{d}t, \nonumber \\ I_{ST}(\xi )&\le \int _{-\infty }^{\xi }\frac{k_{T}+\mu }{\rho _{ST}}e^{\lambda ^{-}_{ST}(\xi -t)}\frac{1}{k_{T}+\mu }f(1-r)\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))S^{0}\mathrm{d}t \nonumber \\&\quad +\int _{\xi }^{+\infty }\frac{k_{T}+\mu }{\rho _{ST}}e^{\lambda ^{+}_{ST}(\xi -t)}\frac{1}{k_{T}+\mu }f(1-r)\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))S^{0}\mathrm{d}t, \nonumber \\ I_{R}(\xi )&\le \int _{-\infty }^{\xi }\frac{k_{R}+\mu }{\rho _{R}}e^{\lambda ^{-}_{R}(\xi -t)}\frac{1}{k_{R}+\mu }[fr\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))+\beta _{R}I_{R}(t)]S^{0}\mathrm{d}t \nonumber \\&\quad +\int _{\xi }^{+\infty }\frac{k_{R}+\mu }{\rho _{R}}e^{\lambda ^{+}_{R}(\xi -t)}\frac{1}{k_{R}+\mu }[fr\beta _{S}(I_{SU}(t)+\delta I_{ST}(t))+\beta _{R}I_{R}(t)]S^{0}\mathrm{d}t. \end{aligned}$$

(21)

Making further simplification of inequalities (21) yields

$$\begin{aligned} I_{SU}(\xi )&\le (V^{-1}F)_{1}\left[ \int _{-\infty }^{\xi }\frac{k_{U}+\mu }{\rho _{SU}}e^{\lambda ^{-}_{SU}(\xi -t)}I(t)\mathrm{d}t+\int _{\xi }^{+\infty }\frac{k_{U}+\mu }{\rho _{SU}}e^{\lambda ^{+}_{SU}(\xi -t)}I(t)\mathrm{d}t\right] ,\nonumber \\ I_{ST}(\xi )&\le (V^{-1}F)_{2}\left[ \int _{-\infty }^{\xi }\frac{k_{T}+\mu }{\rho _{ST}}e^{\lambda ^{-}_{ST}(\xi -t)}I(t)\mathrm{d}t+\int _{\xi }^{+\infty }\frac{k_{T}+\mu }{\rho _{ST}}e^{\lambda ^{+}_{ST}(\xi -t)}I(t)\mathrm{d}t\right] , \nonumber \\ I_{R}(\xi )&\le (V^{-1}F)_{3}\left[ \int _{-\infty }^{\xi }\frac{k_{R}+\mu }{\rho _{R}}e^{\lambda ^{-}_{R}(\xi -t)}I(t)\mathrm{d}t+\int _{\xi }^{+\infty }\frac{k_{R}+\mu }{\rho _{R}}e^{\lambda ^{+}_{R}(\xi -t)}I(t)\mathrm{d}t\right] , \end{aligned}$$

(22)

where $(V^{-1}F)_{i},\,i=1,2,3$ denotes the ith row of the matrix $V^{-1}F$ and

$$\begin{aligned} V^{-1}F=\left( \begin{array}{cccc} \frac{(1-f)\beta _{S}S^{0}}{k_{U}+\mu } &{} \frac{(1-f)\beta _{S}\delta S^{0}}{k_{U}+\mu } &{} 0 \\ \frac{f(1-r)\beta _{S}S^{0}}{k_{T}+\mu } &{} \frac{f(1-r)\beta _{S}\delta S^{0}}{k_{T}+\mu } &{} 0 \\ \frac{fr\beta _{S}S^{0}}{k_{R}+\mu } &{} \frac{fr\beta _{S}\delta S^{0}}{k_{R}+\mu } &{} \frac{\beta _{R}S^{0}}{k_{R}+\mu } \\ \end{array} \right) ,\quad I(t)=\left( \begin{array}{cccc} I_{SU}(t) \\ I_{ST}(t) \\ I_{R}(t) \\ \end{array} \right) . \end{aligned}$$

Let $I^{0}_{j}:=\sup _{\xi \in {\mathbf {R}}} I_{j}(\xi ),~j=SU,ST,R$. Then, $I^{0}:=(I^{0}_{SU}, I^{0}_{ST}, I^{0}_{R})^{T}\ge \mathbf {0}$ and $I^{0}\ne \mathbf {0}$, where T represents the transpose of vectors. Furthermore, by (22), we have

$$\begin{aligned} I^{0}\le (V^{-1}F)I^{0}. \end{aligned}$$

(23)

In Sect. A.2, we have proven that $\rho (V^{-1}F)=\rho (FV^{-1})=R_{C}$. Through the Perron–Frobenius theorem, we see that there exists a vector $P = (p_{1}, p_{2}, p_{3})^{T} \in {\mathbf {R}}^{3}$ with $p_{i} > 0, i=1,2,3$ such that $(V^{-1}F)P = R_{C}P$. As $I^{0}$ is bounded, we can suppose that there exists a constant $\chi > 0$ such that $I^{0}\le \chi P$. Iterating inequalities (23), we have $I^{0}\le (V^{-1}F)^{n}I^{0}\le \chi (V^{-1}F)^{n}P=\chi (R_{C})^{n}P.$

When $R_{C}<1$, by selecting a sufficiently large n, we get $I^{0}={\mathbf {0}}$, which is in contradiction with the assumption. Thus, we complete the proof. $\square$

Theorem 5.1 determines whether nonnegative bounded semi-traveling waves connecting the disease-free equilibrium $E^{0}$ itself exist in the first case of Table 1 in Sect.  3. The extinction of influenza in all local areas will inevitably make it difficult for influenza to spread globally. The results show that the control reproduction number $R_{C}$ is a critical threshold determining whether nonnegative bounded semi-traveling waves exist.

5.1.2 Case II: $R_{RC}>1$, $R_{SC}\ne 1$ and $0<c<c_{1}^{*}$

Theorem 5.2

If $R_{RC}>1$ and $R_{SC}\ne 1$ are satisfied, then for any $c\in (0,c_{1}^{*})$, the diffusive model (2) has no nonnegative bounded semi-traveling waves satisfying the asymptotic boundary condition (13), where $c_{1}^{*}=2\sqrt{d_{R}(k_{R}+\mu )(R_{RC}-1)}$.

Proof

We first define the two-sided Laplace transform by

$$\begin{aligned} \mathcal {L}[U(\cdot )](\lambda ):=\int _{-\infty }^{+\infty }e^{-\lambda t}U(t)\mathrm{d}t, \end{aligned}$$

(24)

for $\lambda \ge 0$.

We can rewrite (24) as follows

$$\begin{aligned} \mathcal {L}[U(\cdot )](\lambda )=\mathcal {L}^{-}[U(\cdot )](\lambda )+\mathcal {L}^{+}[U(\cdot )](\lambda ), \end{aligned}$$

(25)

where $\mathcal {L}^{-}[U(\cdot )](\lambda ):=\int _{-\infty }^{0}e^{-\lambda t}U(t)\mathrm{d}t$ is referred to as the negative one-sided Laplace transform (see Zhang et al. 2016), $\mathcal {L}^{+}[U(\cdot )](\lambda ):=\int _{0}^{+\infty }e^{-\lambda t}U(t)\mathrm{d}t$.

It follows from (25) that, if the function U(t) is bounded in $[0, +\infty )$, the convergence of $\mathcal {L}[U(\cdot )](\lambda )$ is equivalent to that of $\mathcal {L}^{-}[U(\cdot )](\lambda )$. From the definition of $\mathcal {L}^{-}[U(\cdot )](\lambda )$, we can find that $\mathcal {L}^{-}[U(\cdot )](\lambda )$ is increasing in $[0, \lambda ^{*})$, where $\lambda ^{*}=+\infty$ or $\lambda ^{*}<+\infty$ with $\lim _{\lambda \rightarrow \lambda ^{*}}\mathcal {L}[U(\cdot )](\lambda )=+\infty$.

It is easy to verify that the two-sided and negative one-sided Laplace transforms have the following properties:

$$\begin{aligned} \mathcal {L}[U'(\cdot )](\lambda )=\lambda \mathcal {L}[U(\cdot )](\lambda ), \quad \mathcal {L}[U''(\cdot )](\lambda )=\lambda ^{2}\mathcal {L}[U(\cdot )](\lambda ), \end{aligned}$$

and

$$\begin{aligned} \begin{array}{l} \mathcal {L}^{-}[U'(\cdot )](\lambda )=\lambda \mathcal {L}^{-}[U(\cdot )](\lambda )+U(0), \\ \mathcal {L}^{-}[U''(\cdot )](\lambda )=\lambda ^{2}\mathcal {L}^{-}[U(\cdot )](\lambda )+\lambda U(0)+U'(0). \end{array} \end{aligned}$$

(26)

Set $J_{i}(\lambda ):=\mathcal {L}[I_{i}(\cdot )](\lambda ),\,i=SU,ST,$ and $J^{-}_{R}(\lambda ):=\mathcal {L}^{-}[I_{R}(\cdot )](\lambda ),$ for $\lambda \in [0, \lambda ^{*}_{i}),\,i=SU,ST,R$. By Lemma C.1, it follows that $\lambda ^{*}_{i}\ge \eta ,\,i=SU,ST,R$.

The latter three equations of wave Eq. (36) of the diffusive model (2) can be rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} d_{SU}I''_{SU}-cI'_{SU}+[(1-f)\beta _{S}S^{0}-(k_{U}+\mu )]I_{SU} \\ \quad = (1-f)\beta _{S}(S^{0}-S)(I_{SU}+\delta I_{ST})-(1-f)\beta _{S}\delta S^{0} I_{ST}, \\ d_{ST}I''_{ST}-cI'_{ST}+[f(1-r)\beta _{S}S^{0}-(k_{T}+\mu )]I_{ST} \\ \quad = f(1-r)\beta _{S}(S^{0}-S)(I_{SU}+\delta I_{ST})-f(1-r)\beta _{S}S^{0}I_{SU}, \\ d_{R}I''_{R}-cI'_{R}+[\beta _{R}S^{0}-(k_{R}+\mu )]I_{R} \\ \quad = (S^{0}-S)[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]-fr\beta _{S}S^{0}(I_{SU}+\delta I_{ST}). \end{array}\right. \end{aligned}$$

(27)

Define $\upsilon =\min \{P_{R}(\lambda ):\lambda \ge 0\}$, where $P_{R}(\lambda )=d_{R}\lambda ^{2}-c\lambda +\beta _{R}S^{0}-(k_{R}+\mu )$. It follows from the condition $0<c<c_{1}^{*}=2\sqrt{d_{R}(k_{R}+\mu )(R_{RC}-1)}$ that $\upsilon >0$.

Now we suppose that system (2) has a nonnegative semi-traveling wave $(S(\xi )$, $I_{SU}(\xi )$, $I_{ST}(\xi )$, $I_{R}(\xi ))$ satisfying the asymptotic boundary condition (13). According to the boundary condition (13), without loss of generality, we can assume $S^{0}-S(\xi )<\frac{\upsilon }{2}$ for all $\xi <0$. By the third equation of (27), we get

$$\begin{aligned} d_{R}I''_{R}-cI'_{R}+[\beta _{R}S^{0}-(k_{R}+\mu )]I_{R}&= \beta _{R}(S^{0}-S)I_{R}-fr\beta _{S}S(I_{SU}+\delta I_{ST}) \\&\le \beta _{R}(S^{0}-S)I_{R} \le \frac{\upsilon \beta _{R}}{2}I_{R} \le \frac{\upsilon }{2}I_{R}. \end{aligned}$$

Taking the negative one-sided Laplace transform of the above inequality and making use of the properties of $\mathcal {L}^{-}[\cdot ]$ in (26), we obtain

$$\begin{aligned} P_{R}(\lambda )J^{-}_{R}(\lambda )+Q(\lambda )\le \frac{\upsilon }{2}J^{-}_{R}(\lambda ), \end{aligned}$$

(28)

where $Q(\lambda )=(d_{R}\lambda -c)I_{R}(0)+d_{R}I'_{R}(0)$. Therefore, by (28), we have

$$\begin{aligned} \varXi (\lambda ):=\left[ P_{R}(\lambda )-\frac{\upsilon }{2}\right] J^{-}_{R}(\lambda )+Q(\lambda )\le 0. \end{aligned}$$

(29)

If $\lambda ^{*}_{R}<+\infty$, we have $\lim _{\lambda \rightarrow \lambda ^{*-}_{R}}J^{-}_{R}(\lambda )=+\infty$, which implies $\lim _{\lambda \rightarrow \lambda ^{*-}_{R}}\varXi (\lambda )=+\infty$, which is in contradiction with (29). If $\lambda ^{*}_{R}=+\infty$, since $J^{-}_{R}(\lambda )$ is monotonically increasing, together with the definitions of $P_{R}(\lambda )$ and $Q(\lambda )$, we have $\lim _{\lambda \rightarrow \lambda ^{*-}_{R}}\varXi (\lambda )=+\infty$, which is still in contradiction with (29). Thus, the proof of the theorem is completed. $\square$

5.1.3 Case III: $R_{SC}>1$, $R_{RC}\ne 1$ and $0<c<c_{2}^{*}$

Theorem 5.3

If $R_{SC}>1$ and $R_{RC}\ne 1$ are satisfied, then for any $c\in (0,c_{2}^{*})$, the diffusive model (2) has no nonnegative bounded semi-traveling waves satisfying the asymptotic boundary condition (13).

Proof

We prove the theorem by contradiction. For fixed $c\in (0,c_{2}^{*})$, we suppose that there exists a nonnegative bounded semi-traveling wave of the diffusive model (2) satisfying the asymptotic boundary condition (13).

Based on the definition of the two-sided Laplace transform [see (24)] in Sect. 5.1.2, we take the two-sided Laplace transform of first and second equations of (27), yielding

$$\begin{aligned} \left\{ \begin{array}{ll} P_{SU}(\lambda )J_{SU}(\lambda ) = (1-f)\beta _{S}G(\lambda )-(1-f)\beta _{S}\delta S^{0} J_{ST}(\lambda ), \\ P_{ST}(\lambda )J_{ST}(\lambda ) = f(1-r)\beta _{S}G(\lambda )-f(1-r)\beta _{S}S^{0}J_{SU}(\lambda ), \end{array}\right. \end{aligned}$$

(30)

where $G(\lambda )=\mathcal {L}[g(\cdot )](\lambda ),~g(t)=(S^{0}-S)(I_{SU}+\delta I_{ST})$.

Now, we illustrate $\lambda ^{*}_{i}<+\infty , i=SU,ST$. By the first equation of (30), we obtain

$$\begin{aligned} H_{SU}(\lambda ):=[d_{SU}\lambda ^{2}-c\lambda -(k_{U}+\mu )]J_{SU}(\lambda )+(1-f)\beta _{S}\mathcal {L}[S(\cdot )(I_{SU}(\cdot )+\delta I_{ST}(\cdot ))](\lambda )=0. \end{aligned}$$

(31)

By the aid of the two-sided Laplace transform in (24), we have

$$\begin{aligned} J_{SU}(\lambda )>0, \end{aligned}$$

(32)

and, for $\lambda \in [0, \lambda ^{*}_{SU})$,

$$\begin{aligned} \mathcal {L}[S(\cdot )(I_{SU}(\cdot )+\delta I_{ST}(\cdot ))](\lambda )>0. \end{aligned}$$

(33)

If $\lambda ^{*}_{SU}=+\infty$, using (32) and (33), we get $H_{SU}(+\infty )=+\infty$, which is in contradiction with (31). So we can conclude that $\lambda ^{*}_{SU}<+\infty$. Similarly, we can also prove that $\lambda ^{*}_{ST}<+\infty$.

Then, we show $\lambda ^{*}_{SU}=\lambda ^{*}_{ST}$. Assume that $\lambda ^{*}_{SU}<\lambda ^{*}_{ST}$, which means $\lim _{\lambda \rightarrow \lambda ^{*}_{SU}}J_{SU}(\lambda )$ $=+\infty$ and $\lim _{\lambda \rightarrow \lambda ^{*}_{SU}}J_{ST}(\lambda )=J_{ST}(\lambda ^{*}_{SU})<+\infty$. From Lemma C.1 and the definition of the two-sided Laplace transform in (24), together with the boundedness of semi-traveling waves, we know that $G(\lambda ^{*}_{SU})<+\infty$, which follows that the second equation of (30) does not hold. So, $\lambda ^{*}_{SU}\ge \lambda ^{*}_{ST}$. On the other hand, we suppose that $\lambda ^{*}_{SU}>\lambda ^{*}_{ST}$, by a similar discussion, we have $\lambda ^{*}_{SU}\le \lambda ^{*}_{ST}$. Based on the above analysis, we can get the conclusion that $\lambda ^{*}:=\lambda ^{*}_{SU}=\lambda ^{*}_{ST}$.

Next, let us further consider $P_{SU}(\lambda ^{*})$ and $P_{ST}(\lambda ^{*})$. If $P_{SU}(\lambda ^{*})\ge 0$, we have

$$\begin{aligned} P_{SU}(\lambda ^{*})J_{SU}(\lambda ^{*})+(1-f)\beta _{S}\delta S^{0} J_{ST}(\lambda ^{*}) = +\infty >(1-f)\beta _{S}G(\lambda ^{*}), \end{aligned}$$

which is in contradiction with the first equation of (30). So, we have $P_{SU}(\lambda ^{*})<0$. Similarly, we can also prove $P_{ST}(\lambda ^{*})<0$.

Finally, we multiply the first equation by the second one of (30), yielding

$$\begin{aligned} H(\lambda )J_{SU}(\lambda )J_{ST}(\lambda ) = f(1-f)(1-r)\beta ^{2}_{S}G(\lambda )[G(\lambda )-S^{0}(J_{SU}(\lambda )+\delta J_{ST}(\lambda ))]. \end{aligned}$$

Consequently, we have

$$\begin{aligned} H(\lambda ^{*})={\displaystyle \lim _{\lambda \rightarrow \lambda ^{*-}} } \frac{f(1-f)(1-r)\beta ^{2}_{S}G(\lambda )[G(\lambda )-S^{0}(J_{SU}(\lambda )+\delta J_{ST}(\lambda ))]}{J_{SU}(\lambda )J_{ST}(\lambda )}=0, \end{aligned}$$

which is in contradiction with Lemma C.2. Therefore, the proof is completed. $\square$

Combined with Lemma C.1, Theorems 5.2 and 5.3, we can give the following proposition directly.

Proposition 5.4

If $R_{C}>1$ and $R_{i}\ne 1, i=SC,RC$ are satisfied, then for any $c\in (0,\min \{c_{1}^{*},c_{2}^{*}\})$, the diffusive model (2) has no nonnegative bounded semi-traveling waves satisfying the asymptotic boundary condition (13).

When the control reproduction number $R_{C}$ is greater than 1, the range of the wave speed c determines whether nonnegative traveling waves exist. Fixed $R_{C}>1$, the diffusion rates of three infectious subclasses affect the critical wave speeds $c_{1}^{*}$ and $c_{2}^{*}$, determining the possibility of the existence of nonnegative traveling waves. From the expressions of $c_{1}^{*}$ and $c_{2}^{*}$ (see Theorem 5.2 and Lemma C.2), we can see that the critical wave speed $c_{1}^{*}$ is related to the diffusion coefficient $d_{R}$ of resistant strain, while the critical wave speed $c_{2}^{*}$ is related to the diffusion coefficients $d_{SU}$ and $d_{ST}$ of sensitive strains. When $R_{C}>1$, influenza will spread locally in a certain area. If $R_{RC}>1$, then $c_{1}^{*}>0$, indicating that the movement of individuals with resistant strains will accelerate the spatial spread of influenza. If $R_{SC}>1$, then $c_{2}^{*}>0$, indicating that the movement of individuals with sensitive strains will play an important role in the spatial spread of influenza. In short, the movement of infected individuals in space increases the possibility of a global outbreak of influenza.

5.2 Estimation of Minimal Wave Speed

The minimal wave speed for a traveling wave is a key parameter to characterize the speed at which the disease spreads in a spatial domain (Huang 2016; Zhang 2017; Zhang et al. 2016). Biologically speaking, epidemics can spread for $c\ge c_{\min }$ while they cannot spread for any $c<c_{\min }$, where $c_{\min }$ is minimal wave speed, an important threshold value to determine whether epidemics can spread or not. Proposition 5.4 provides the basis for our estimation of the range of minimal wave speed. Combining with Theorem 4.5, we can conjecture that minimal wave speed $c_{\min }$ of the diffusive model (2) satisfies $c_{\min }\in [\min \{c_{1}^{*},c_{2}^{*}\}, c^{*}]$. We find that the lower bound of minimal wave speed $c_{\min }$ depends on the minimum value of minimal wave speeds of its two subsystems where $I_{R}=0$ or $I_{SU}=I_{ST}=0$, which seems to be a new phenomenon. This also provides suggestions for us to control influenza in reality. By calculating the minimal wave speeds of two kinds of strains, an optimal scheme for influenza control can be scientifically formulated.

6 Conclusions and Discussions

Antiviral treatment remains a major pharmaceutical intervention in the management of influenza infection. This is particularly important in the absence of preventive measures (such as vaccination). However, antiviral resistance may develop during the treatment of drug-sensitive strains. The emergence and spread of resistant strains during influenza pandemics has the possibility of causing major morbidity and mortality, becoming one of the most challenging public health issues. To better understand the temporal and spatial characteristics of influenza transmission and reduce the risk of future influenza pandemic, in this paper, we incorporate antiviral resistance, population diffusion and demographic processes (recruitment and natural deaths) into the previous influenza models, forming a diffusive influenza model (1) with multiple strains, where a population is divided into five disjoint classes: susceptible individuals, individuals infected with the sensitive strain and untreated, individuals infected with the sensitive strain and treated, individuals infected with the resistant strain and recovered individuals.

First of all, we analyze its corresponding reaction model. By solving algebraic equations, we find all equilibria of the reaction model (3) and the corresponding conditions that guarantee their existence (see Table 1). There are three possible equilibria for the reaction model, i.e., two boundary equilibria (the disease-free equilibrium $E^{0}$ and the boundary equilibrium $\hat{E}$) and an interior (positive) equilibrium $E^{*}$. We introduce three parameters, $R_{SC}$, $R_{RC}$ and $R_{C}$, to determine the region where each equilibrium exists. The disease-free equilibrium $E^{0}$ always exists. When the reproduction numbers of both strains are less than one, then all strains will die out. When at least one of the reproduction numbers is greater than one, the strain with the higher reproduction number is certain to persist. If the reproduction number $R_{SC}$ of the drug-sensitive strains is greater than 1 and exceeds the reproduction number $R_{RC}$ of the drug-resistant strain, then there is an equilibrium state at which three pathogen strains are present. If the reproduction number $R_{RC}$ of the drug-resistant strain is greater than 1, then there is an equilibrium state at which only the drug-resistant strain is present. We conjecture that the single-strain (drug-resistant strain) equilibrium is globally asymptotically stable when $R_{RC}>1$ and $R_{RC}>R_{SC}$. In general, the sensitive strain is the one that is more dominant, but it can be eliminated by treatment. Depending on the reproduction number of the drug-resistant strain, if increasing the treatment rate reduces the reproduction number of the drug-sensitive strains to a value below the reproduction number of the drug-resistant strain, then influenza may move the three-strain equilibrium state to the disease-free equilibrium state or to the boundary equilibrium state where only drug-resistant infection is present.

Next, we study the existence of the three kinds of traveling waves in the diffusive model (2) which starts from the disease-free equilibrium $E^{0}$ (at the initial stage of influenza transmission): semi-traveling waves, strong traveling waves and persistent traveling waves. As it is well known, traveling waves starting from the disease-free equilibrium are of biological significance since we can get a lot of information from them, such as whether epidemics will spread, asymptotic speed of propagation and the final state of the wavefront. Note that the diffusive model (2) is a non-monotone system containing four equations and is full of complexity (such as time-varying population and crossed reaction items), some dynamical problems on this system become very challenging. To over those difficulties, we first technically introduce the auxiliary system (35). Then, a bounded cone is achieved through a pair of upper–lower solutions associated with Schauder’s fixed-point theorem. The existence of positive semi-traveling waves of the diffusive model (2) is obtained by the limiting techniques and Arzelà–Ascoli theorem, and a prior estimate of exponential decay of semi-traveling waves is made. We find that the existence of positive semi-traveling waves starting from the disease-free equilibrium $E^{0}$ is jointly decided by the control reproduction number $R_{C}$ and the critical wave speed $c^{*}$. On the basis of the existence of semi-traveling waves, we construct an appropriate Lyapunov functional and use LaSalle’s invariance principle to obtain the existence condition of strong traveling waves connecting the disease-free equilibrium $E^{0}$ and boundary equilibrium $\hat{E}$ for the diffusive model (2). The results show that if strong traveling waves connecting $E^{0}$ and $\hat{E}$ exist, in addition to $R_{C}>1$ and $c>c^{*}$, it also requires $R_{SU}\le R_{R}$ and $R_{ST}\le R_{R}$. Furthermore, persistence theory of dynamical systems is creatively applied to prove the existence of persistent traveling waves starting from the disease-free equilibrium $E^{0}$. In this case, we have more stringent requirements on the reproduction numbers and the wave speed, that is, $R_{SC}>1>R_{RC}$ and $c>\max \{c^{*}, \tilde{c}^{*}\}$.

In view of these three types of traveling waves, we give some biological interpretations about their analytical results in each subsection, respectively. Biologically, the existence of semi-traveling waves starting from the disease-free equilibrium $E^{0}$ indicates that the spread of influenza will occur. The existence of strong traveling waves which connect the disease-free equilibrium $E^{0}$ and boundary equilibrium $\hat{E}$ indicates that there is a transition zone moving from the steady state with no infective individuals to the steady state with only drug-resistant infected individuals. In particular, the presence of persistent traveling waves indicates that the infection with sensitive and resistant strains does not disappear at the end of the wavefront.

On the other hand, the nonexistence of nonnegative bounded semi-traveling waves connecting the disease-free steady state $E^{0}$ itself in three cases is proved by the comparison principle, the negative one-sided and two-sided Laplace transforms. We show that the diffusive model (2) has no nontrivial traveling waves when (i) $R_{C}<1$ and $c>0$; (ii) $R_{RC}>1$, $R_{SC}\ne 1$ and $0<c<c_{1}^{*}$; or (iii) $R_{SC}>1$, $R_{RC}\ne 1$ and $0<c<c_{2}^{*}$. When the control reproduction number $R_{C}$ is larger than 1, the conditions for the existence and nonexistence of traveling waves for the diffusive model (2) are determined completely by the reproduction numbers $R_{SC}$, $R_{RC}$ and the wave speed c. Theorem 4.5 and Proposition 5.4 combined provide an interval estimation of minimal wave speed $c_{min}$, which satisfies $c_{min}\in [\min \{c_{1}^{*},c_{2}^{*}\}, c^{*}]$.

In this study, we consider the use of antiviral treatment and population diffusion in order to gain more insights on the implementation of control measures of influenza among human population. Antiviral resistance in influenza may have devastating consequences, which poses a significant challenge in the control of influenza. Our findings demonstrate that the control of influenza depends not only on the rates of resistance emergence and transmission during treatment, but also on the diffusion rates of influenza strains, which has been overlooked in previous modeling studies. This suggests that antiviral treatment should be implemented appropriately, and infected individuals (especially with the resistant strain) should be tested and controlled effectively. The current study provides two policy recommendations: (i) apply control theory to find the optimal timing and level of treatment profile that minimize the cumulative number of infections (i.e., the epidemic final size) and resistance; (ii) make scientific screening for people in disaster areas and restrict infected individuals’ travel, providing sufficient time for vaccine development and the preparation of treatment regime. The model presented in this work provides a simplified framework for the dynamics of drug resistance emergence and diffusion in the population and has important guiding significance for mathematical epidemiological modeling in general.

Finally, we should remark that although we discover some rich dynamical behaviors for a diffusive influenza model (1) with multiple strains, there are quite a few problems that deserve further investigation in future work. For example, we have not showed whether the critical wave speed $c^{*}$ is equal to the minimal wave speed $c_{\min }$, that is, we have not completely determined the nonexistence of nonnegative bounded traveling wave solutions connecting the disease-free equilibrium $E^{0}$ for $0<c <c^{*}$. Moreover, from the viewpoint of mathematical biology, it is an important problem to consider the asymptotic speeding of the diffusive model (2). We here conjecture that $c^{*}$ is the asymptotic speeding of the diffusive model (2); however, we do not verify it and we also leave it for another future work.

Appendices

Semi-traveling Waves for the Auxiliary System

1.1 An Auxiliary System

An auxiliary system related to the diffusive model (2) can be described by

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial S}{\partial t} = d_{S}\frac{\partial ^{2} S}{\partial x^{2}}+\varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ \frac{\partial I_{SU}}{\partial t} = d_{SU}\frac{\partial ^{2} I_{SU}}{\partial x^{2}}+(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU}-\varUpsilon I^{2}_{SU}, \\ \frac{\partial I_{ST}}{\partial t} = d_{ST}\frac{\partial ^{2} I_{ST}}{\partial x^{2}}+f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST}-\varUpsilon I^{2}_{ST}, \\ \frac{\partial I_{R}}{\partial t} = d_{R}\frac{\partial ^{2} I_{R}}{\partial x^{2}}+[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S-(k_{R}+\mu )I_{R}-\varUpsilon I^{2}_{R}, \end{array}\right. \end{aligned}$$

(34)

where $\varUpsilon$ is a small positive constant.

Substituting the wave profile $S(x,t)=S(\xi ), I_{i}(x,t)=I_{i}(\xi )$, $i = SU, ST, R$, $x+ct=\xi$ into (34), we obtain the corresponding wave equations

$$\begin{aligned} \left\{ \begin{array}{ll} cS' = d_{S}S''+\varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ cI'_{SU} = d_{SU}I''_{SU}+(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU}-\varUpsilon I^{2}_{SU}, \\ cI'_{ST} = d_{ST}I''_{ST}+f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST}-\varUpsilon I^{2}_{ST}, \\ cI'_{R} = d_{R}I''_{R}+[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S-(k_{R}+\mu )I_{R}-\varUpsilon I^{2}_{R}. \end{array}\right. \end{aligned}$$

(35)

The limiting equations of (35) when $\varUpsilon \rightarrow 0$ become the wave equations of the diffusive model (2). For the convenience of use, we give their specific form as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} cS' = d_{S}S''+\varLambda -\mu S-[\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S, \\ cI'_{SU} = d_{SU}I''_{SU}+(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{U}+\mu )I_{SU}, \\ cI'_{ST} = d_{ST}I''_{ST}+f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S-(k_{T}+\mu )I_{ST}, \\ cI'_{R} = d_{R}I''_{R}+[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S-(k_{R}+\mu )I_{R}. \end{array}\right. \end{aligned}$$

(36)

1.2 Linearization of the Wave System at $E^{0}$

Linearizing system (36) at the equilibrium $E^{0}(S^{0},0,0,0)$ and only considering the last three equations of the linearized system, we have

$$\begin{aligned} \left\{ \begin{array}{ll} c\varphi '_{2} = d_{SU}\varphi ''_{2}+(1-f)\beta _{S}(\varphi _{2}+\delta \varphi _{3})S^{0}-(k_{U}+\mu )\varphi _{2}, \\ c\varphi '_{3} = d_{ST}\varphi ''_{3}+f(1-r)\beta _{S}(\varphi _{2}+\delta \varphi _{3})S^{0}-(k_{T}+\mu )\varphi _{3}, \\ c\varphi '_{4} = d_{R}\varphi ''_{4}+[fr\beta _{S}(\varphi _{2}+\delta \varphi _{3})+\beta _{R}\varphi _{4}]S^{0}-(k_{R}+\mu )\varphi _{4}, \end{array}\right. \end{aligned}$$

(37)

where the functions $\varphi _{i}(\xi ),\,i=2,3,4$ correspond to $I_{j}(\xi ),\,j=SU,ST,R$, respectively.

We look for the solutions with the form $(\varphi _{2}(\xi ),\varphi _{3}(\xi ),\varphi _{4}(\xi )) = e^{\lambda \xi }(\kappa _{2},\kappa _{3},\kappa _{4})$, where $\kappa _{i}>0,\,i=2, 3, 4$ and $\lambda >0$. Substituting them into Eq. (37), we obtain the following eigenvalue equations

$$\begin{aligned} \left\{ \begin{array}{ll} c\lambda \kappa _{2} = d_{SU}\lambda ^{2}\kappa _{2}+(1-f)\beta _{S}(\kappa _{2}+\delta \kappa _{3})S^{0}-(k_{U}+\mu )\kappa _{2}, \\ c\lambda \kappa _{3} = d_{ST}\lambda ^{2}\kappa _{3}+f(1-r)\beta _{S}(\kappa _{2}+\delta \kappa _{3})S^{0}-(k_{T}+\mu )\kappa _{3}, \\ c\lambda \kappa _{4} = d_{R}\lambda ^{2}\kappa _{4}+[fr\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]S^{0}-(k_{R}+\mu )\kappa _{4}. \end{array}\right. \end{aligned}$$

(38)

Let $\tilde{A} = \mathrm{diag}(d_{SU},d_{ST},d_{R}), \tilde{B} = \mathrm{diag}(c,c,c)$ and $\widetilde{M}(\lambda ,c) := \tilde{A}\lambda ^{2}-\tilde{B}\lambda +F-V$, where the matrices F and V are given by (4) and (5). Then, by denoting $\mathcal {K} = (\kappa _{2},\kappa _{3},\kappa _{4})^{T}$, the eigenvalue Eq. (38) can be rewritten as $\widetilde{M}(\lambda ,c) \mathcal {K} = 0$. By the transformations $A = V^{-1}\tilde{A}$ and $B = V^{-1}\tilde{B}$, we obtain an equivalent form of these equations as follows $M(\lambda ,c)\mathcal {K} = \mathcal {K},$ with $M(\lambda ,c) = (-A\lambda ^{2}+B\lambda +I)^{-1}(V^{-1}F)$, which is

$$\begin{aligned}M(\lambda ,c) = \left( \begin{array}{cccc} \frac{(1-f)\beta _{S}S^{0}}{\varTheta _{2}(\lambda , c)} &{} \frac{(1-f)\beta _{S}\delta S^{0}}{\varTheta _{2}(\lambda , c)} &{} 0 \\ \frac{f(1-r)\beta _{S}S^{0}}{\varTheta _{3}(\lambda , c)} &{} \frac{f(1-r)\beta _{S}\delta S^{0}}{\varTheta _{3}(\lambda , c)} &{} 0 \\ \frac{fr\beta _{S}S^{0}}{\varTheta _{4}(\lambda , c)} &{} \frac{fr\beta _{S}\delta S^{0}}{\varTheta _{4}(\lambda , c)} &{} \frac{\beta _{R}S^{0}}{\varTheta _{4}(\lambda , c)} \\ \end{array} \right) , \end{aligned}$$

where $\varTheta _{2}(\lambda , c) = -d_{SU}\lambda ^{2}+c\lambda +k_{U}+\mu ,$ $\varTheta _{3}(\lambda , c) = -d_{ST}\lambda ^{2}+c\lambda +k_{T}+\mu$ and $\varTheta _{4}(\lambda , c) = -d_{R}\lambda ^{2}+c\lambda +k_{R}+\mu$.

Denoting $d = \max \{d_{SU}, d_{ST}, d_{R}\}$, since $\varTheta _{i}\left( \frac{c}{2d}, c\right)$ is strictly increasing and nonnegative in $c\in [0,+\infty )$, we can deduce that the matrix $M\left( \frac{c}{2d},c\right)$ is decreasing for $c\in [0,+\infty )$.

Denote by $\rho (M(\lambda ,c))$ the principal eigenvalue of the nonnegative matrix $M(\lambda ,c)$ for $\lambda \in \left[ 0,\frac{c}{2d}\right]$. Since $\rho (M(\lambda ,c))$ is continuous and monotonically increasing with respect to the nonnegative matrix $M(\lambda ,c)$, $\rho \left( M\left( \frac{c}{2d},c\right) \right)$ is strictly decreasing in $c\in [0,+\infty )$. In particular, we have $\rho (M(0,0)) = \rho (V^{-1}F)$, and $\lim _{c\rightarrow +\infty }\rho \left( M\left( \frac{c}{2d},c\right) \right) =0$.

For the continuation of the analysis, here, we give a brief proof of $\rho (V^{-1}F)=R_{C}$. By the definition of the control reproduction number $R_{C}$ in (9), we know $R_{C}=\rho (FV^{-1})$, implying that $R_{C}$ is the Perron–Frobenius eigenvalue of the matrix $FV^{-1}$. So there exists a positive eigenvector $P=(p_{1}, p_{2}, p_{3})^T$ with $p_{i}>0,\,i=1,2,3$ such that $(FV^{-1})P=R_{C}P$. Then, we have $V^{-1}P>0$ and $(V^{-1}F)(V^{-1}P)=V^{-1}(FV^{-1})P=R_{C}V^{-1}P$. This implies that $R_{C}$ is a nonnegative eigenvalue of the matrix $V^{-1}F$ with positive eigenvector $V^{-1}P$. It is easy to see that $V^{-1}F$ is irreducible, that is, $(V^{-1}F+I)^{2}>0$. Using Perron–Frobenius theorem, we get $\rho (V^{-1}F)=R_{C}$.

Combining with $\rho (M(0,0)) = \rho (V^{-1}F)$ yields $\rho (M(0,0)) = R_{C}$. Consequently, when $R_{C}>1$, there exists a unique $c^{*}>0$ such that

$$\begin{aligned}\rho (M(\frac{c}{2d},c))\left\{ \begin{array}{ll} >1, &{}\quad c\in [0,c^{*}); \\ =1, &{}\quad {c = c^{*};} \\ <1, &{} \quad {c\in (c^{*},+\infty ).} \end{array} \right. \end{aligned}$$

Now we fix $c>c^{*}$, note that $\varTheta _{i}(\lambda , c) (i=2,3,4)$ is strictly increasing in $\lambda \in \left[ 0,\frac{c}{2d}\right]$, then we obtain that $\rho (M(\lambda ,c))$ is strictly decreasing and nonnegative in $\lambda \in \left[ 0,\frac{c}{2d}\right]$. In view of the facts $\rho (M(0,c)) = \rho (M(0,0)) = R_{C}>1$ and $\rho \left( M\left( \frac{c}{2d},c\right) \right) <1$, then there exists a $\lambda _{c}\in \left( 0,\frac{c}{2d}\right)$ such that

$$\begin{aligned} \rho (M(\lambda ,c))\left\{ \begin{array}{ll} >1, &{} \quad {\lambda \in [0,\lambda _{c});} \\ =1, &{} \quad {\lambda = \lambda _{c};} \\ <1, &{} \quad {\lambda \in \left( \right. \lambda _{c},\frac{c}{2d}\left. \right] .} \end{array} \right. \end{aligned}$$

Based on the above discussions, we have the following lemma.

Lemma A.1

Assume that $R_{C} = \rho (FV^{-1})>1$. Then, there exists $c^{*}>0$ such that for any $c>c^{*}$, we can always find $\lambda _{c}\in (0,\frac{c}{2d})$ and $\mathcal {K}_{c}=(\kappa _{2},\kappa _{3},\kappa _{4})^{T}$ with $\kappa _{i}>0,\,i=2,3,4$ satisfying $\det \widetilde{M}(\lambda _{c},c)=0$ and $\widetilde{M}(\lambda _{c},c)\mathcal {K}_{c}=0$.

Proof

It follows from the above arguments that $\rho (M(\lambda _{c},c))=1$. By the Perron–Frobenius theorem, we conclude that there is a vector $\mathcal {K}_{c}\in {\mathbf {R}}^{3}$ with positive components such that $M(\lambda _{c},c)\mathcal {K}_{c}=\mathcal {K}_{c}$. Multiplying the matrix $-A\lambda _{c}^{2}+B\lambda _{c}+I$ on both sides of the above equality, we have $(A\lambda _{c}^{2}-B\lambda _{c}+V^{-1}F-I)\mathcal {K}_{c}=0$. Multiplying the diagonal matrix V to both sides of the above equality, we finally obtain $(\tilde{A}\lambda _{c}^{2}-\tilde{B}\lambda _{c}+F-V)\mathcal {K}_{c}=\widetilde{M}(\lambda _{c},c)\mathcal {K}_{c}=0$. This completes the proof. $\square$

Let $\mathcal {K}_{c}=(\kappa _{2},\kappa _{3},\kappa _{4})^{T}$ as obtained in Lemma A.1, then the following lemma is straightforward.

Lemma A.2

The vector valued function $\varphi (\xi )=(\varphi _{2}(\xi ),\varphi _{3}(\xi ),\varphi _{4}(\xi ))$ with $\varphi _{i}(\xi )=\kappa _{i}e^{\lambda _{c}\xi }$, $i=2,3,4$ satisfies Eq. (37).

1.3 Construction and Properties of Upper–Lower Solutions

In the next subsection, by using the Schauder’s fixed-point theorem, we establish the existence of semi-traveling waves of the auxiliary system (35). For this purpose, we need to define a pair of upper–lower solutions of system (35) as follows.

$$\begin{aligned} \begin{array}{ll} \bar{S}(\xi ) := S^{0},&{}\quad \underline{S}(\xi ) := \max \{S^{0}-\sigma e^{\alpha \xi }, 0\}, \\ \bar{I}_{SU}(\xi ) := \min \{\kappa _{2}e^{\lambda _{c}\xi }, \kappa _{2}K^{*}\},&{}\quad \underline{I}_{SU}(\xi ) := \max \{\kappa _{2}e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi }), 0\}, \\ \bar{I}_{ST}(\xi ) := \min \{\kappa _{3}e^{\lambda _{c}\xi }, \kappa _{3}K^{*}\},&{}\quad \underline{I}_{ST}(\xi ) := \max \{\kappa _{3}e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi }), 0\}, \\ \bar{I}_{R}(\xi ) := \min \{\kappa _{4}e^{\lambda _{c}\xi }, \kappa _{4}K^{*}\},&{}\quad \underline{I}_{R}(\xi ) := \max \{\kappa _{4}e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi }), 0\}, \end{array} \end{aligned}$$

(39)

where the constants $\kappa _{2}, \kappa _{3}, \kappa _{4}$ and $\lambda _{c}$ have been determined in Lemma A.1. The positive constants $K^{*}, \sigma , \alpha , Q, \varepsilon$ will be determined later.

We next show that such constructed upper and lower solutions satisfy some properties in Lemmas A.3, A.4 and A.5.

Lemma A.3

For $K^{*}>1$ large enough, the functions $\bar{I}_{SU}(\xi ), \bar{I}_{ST}(\xi )$ and $\bar{I}_{R}(\xi )$ satisfy the following inequalities

$$\begin{aligned} \left\{ \begin{array}{l} c\bar{I}'_{SU} \ge d_{SU}\bar{I}''_{SU}+(1-f)\beta _{S}(\bar{I}_{SU}+\delta \bar{I}_{ST})S^{0}-(k_{U}+\mu )\bar{I}_{SU}-\varUpsilon \bar{I}^{2}_{SU}, \\ c\bar{I}'_{ST} \ge d_{ST}\bar{I}''_{ST}+f(1-r)\beta _{S}(\bar{I}_{SU}+\delta \bar{I}_{ST})S^{0}-(k_{T}+\mu )\bar{I}_{ST}-\varUpsilon \bar{I}^{2}_{ST}, \\ c\bar{I}'_{R} \ge d_{R}\bar{I}''_{R}+[fr\beta _{S}(\bar{I}_{SU}+\delta \bar{I}_{ST})+\beta _{R}\bar{I}_{R}]S^{0}-(k_{R}+\mu )\bar{I}_{R}-\varUpsilon \bar{I}^{2}_{R}, \end{array}\right. \end{aligned}$$

(40)

for any $\xi \ne \xi _{1}:=\frac{\ln K^{*}}{\lambda _{c}}$.

Proof

Define the operator $L[I_{SU}(\cdot ),I_{ST}(\cdot ),I_{R}(\cdot )](\xi ):=$

$$\begin{aligned} \left( \begin{array}{l} d_{SU}I''_{SU}-cI'_{SU} +(1-f)\beta _{S}(I_{SU}+\delta I_{ST})S^{0}-(k_{U}+\mu )I_{SU} \\ d_{ST}I''_{ST}-cI'_{ST}+f(1-r)\beta _{S}(I_{SU}+\delta I_{ST})S^{0}-(k_{T}+\mu )I_{ST} \\ d_{R}I''_{R}-cI'_{R}+[fr\beta _{S}(I_{SU}+\delta I_{ST})+\beta _{R}I_{R}]S^{0}-(k_{R}+\mu )I_{R} \\ \end{array}\right) , \end{aligned}$$

then (40) can be transformed into the following equivalent operator inequalities

$$\begin{aligned} L[I_{SU}(\cdot ),I_{ST}(\cdot ),I_{R}(\cdot )](\xi )\le \varUpsilon \left( \bar{I}^{2}_{SU},\bar{I}^{2}_{ST},\bar{I}^{2}_{R}\right) . \end{aligned}$$

(41)

So, as long as we prove operator inequality (41), we complete the proof of Lemma A.3. We now prove operator inequalities (41) in two cases:

When $\xi <\xi _{1}$, by the definition of the upper solutions in (39), we have

$$\begin{aligned} \left( \bar{I}_{SU}(\xi ), \bar{I}_{ST}(\xi ), \bar{I}_{R}(\xi )\right) =(\kappa _{2}, \kappa _{3}, \kappa _{4})e^{\lambda _{c}\xi }. \end{aligned}$$

Substituting it into the equations of operator L yields

$$\begin{aligned} L[I_{SU}(\cdot ),I_{ST}(\cdot ),I_{R}(\cdot )](\xi )= e^{\lambda _{c}}\widetilde{M}(\lambda _{c},c)\mathcal {K}_{c}=0. \end{aligned}$$

Obviously, operator inequalities (41) hold.

When $\xi >\xi _{1}$, by (39), we have $(\bar{I}_{SU}(\xi ), \bar{I}_{ST}(\xi ), \bar{I}_{R}(\xi ))=(\kappa _{2}, \kappa _{3}, \kappa _{4})K^{*}$. Taking the first inequality of operator inequalities (41) as an example, we substitute the upper solutions into it, yielding

$$\begin{aligned}&d_{SU}\bar{I}''_{SU}-c\bar{I}'_{SU}+(1-f)\beta _{S}(\bar{I}_{SU}+\delta \bar{I}_{ST})S^{0}-(k_{U}+\mu )\bar{I}_{SU}-\varUpsilon \bar{I}^{2}_{SU} \\&\quad =\left\{ [(1-f)\beta _{S}S^{0}-(k_{U}+\mu )]\kappa _{2}+(1-f)\beta _{S}\delta S^{0}\kappa _{3}-\varUpsilon \kappa ^{2}_{2}K^{*}\right\} K^{*}. \end{aligned}$$

To ensure that the value of the above equality is smaller or equal to 0, we require

$$\begin{aligned} K^{*}>\frac{[(1-f)\beta _{S}S^{0}-(k_{U}+\mu )]\kappa _{2}+(1-f)\beta _{S}\delta S^{0}\kappa _{3}}{\varUpsilon \kappa ^{2}_{2}}. \end{aligned}$$

To make the remaining two inequalities of operator inequalities (41) also hold, similarly, we can choose

$$\begin{aligned} K^{*}>\frac{f(1-r)\beta _{S}S^{0}\kappa _{2}+[f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )]\kappa _{3}}{\varUpsilon \kappa ^{2}_{3}}, \end{aligned}$$

and

$$\begin{aligned} K^{*}>\frac{fr\beta _{S}S^{0}(\kappa _{2}+\delta \kappa _{3})+[\beta _{R}S^{0}-(k_{R}+\mu )]\kappa _{4}}{\varUpsilon \kappa ^{2}_{4}}. \end{aligned}$$

By selecting $K^{*}>1$ satisfying the above three inequalities, we complete the proof of operator inequalities (41) when $\xi >\xi _{1}$. Overall, the proof of the lemma is completed. $\square$

Lemma A.4

For $0<\alpha <\min \left\{ \frac{c}{d_{S}}, \lambda _{c}\right\}$, $\sigma >\max \left\{ S^{0},\frac{[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]S^{0}}{(c-d_{S}\alpha )\alpha +\mu }\right\}$, the function $S(\xi )$ satisfies the following inequality

$$\begin{aligned} c\underline{S}' \le d_{S}\underline{S}''+\varLambda -\mu \underline{S}-[\beta _{S}(\bar{I}_{SU}+\delta \bar{I}_{ST})+\beta _{R}\bar{I}_{R}]\underline{S} \end{aligned}$$

(42)

for any $\xi \ne \xi _{2}:=\frac{1}{\alpha }\ln \frac{S^{0}}{\sigma }$.

Proof

If $\xi >\xi _{2}$, then $\underline{S}(\xi ) = 0$. Obviously, the inequality (42) holds.

If $\xi <\xi _{2}$, then $\underline{S}(\xi ) = S^{0}-\sigma e^{\alpha \xi }$. From the choice of $K^{*}$ and $\sigma$, we know that $\xi _{2}=\frac{1}{\alpha }\ln \frac{S^{0}}{\sigma }<0<\xi _{1}$, implying $(\bar{I}_{SU}(\xi ), \bar{I}_{ST}(\xi ), \bar{I}_{R}(\xi ))=(\kappa _{2}, \kappa _{3}, \kappa _{4})e^{\lambda _{c}\xi }$ when $\xi <\xi _{2}$. Through direct calculations, we have

$$\begin{aligned}&d_{S}\underline{S}''-c\underline{S}'+\varLambda -\mu \underline{S}-[\beta _{S}(\bar{I}_{SU}+\delta \bar{I}_{ST})+\beta _{R}\bar{I}_{R}]\underline{S} \\&\quad =-d_{S}\sigma \alpha ^{2} e^{\alpha \xi }+c\sigma \alpha e^{\alpha \xi }+\varLambda -\mu (S^{0}-\sigma e^{\alpha \xi }) \\&\qquad -[\beta _{S}(\kappa _{2}e^{\lambda _{c}\xi }+\delta \kappa _{3}e^{\lambda _{c}\xi })+\beta _{R}\kappa _{4}e^{\lambda _{c}\xi }](S^{0}-\sigma e^{\alpha \xi }) \\&\quad = \{c\sigma \alpha +\mu \sigma -d_{S}\sigma \alpha ^{2}-[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}](S^{0}-\sigma e^{\alpha \xi })e^{(\lambda _{c}-\alpha )\xi }\}e^{\alpha \xi } \\&\quad \ge \{(c\alpha +\mu -d_{S}\alpha ^{2})\sigma -[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]S^{0}\}e^{\alpha \xi } \ge 0, \end{aligned}$$

where we use the fact that $e^{(\lambda _{c}-\alpha )\xi }<1$ due to $\alpha <\lambda _{c}$ and $\xi <0$, and the conditions that $0<\alpha <\frac{c}{d_{S}}$ and $\sigma >\frac{[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]S^{0}}{(c-d_{S}\alpha )\alpha +\mu }$. Thus, the proof is completed. $\square$

Lemma A.5

Let $\varepsilon >0$ be small enough with $\varepsilon<\alpha , \varepsilon <\lambda _{c}$ and $\lambda _{c}+\varepsilon <\frac{c}{2d}$, then for sufficiently large $Q>1$, and for any $\xi \ne \xi _{3}:=-\frac{\ln Q}{\varepsilon }$, the functions $\underline{I}_{SU}(\xi ), \underline{I}_{ST}(\xi )$ and $\underline{I}_{R}(\xi )$ satisfy the following inequalities

$$\begin{aligned} \left\{ \begin{array}{ll} c\underline{I}'_{SU} \le d_{SU}\underline{I}''_{SU}+(1-f)\beta _{S}(\underline{I}_{SU}+\delta \underline{I}_{ST})\underline{S}-(k_{U}+\mu )\underline{I}_{SU}-\varUpsilon \underline{I}^{2}_{SU}, \\ c\underline{I}'_{ST} \le d_{ST}\underline{I}''_{ST}+f(1-r)\beta _{S}(\underline{I}_{SU}+\delta \underline{I}_{ST})\underline{S}-(k_{T}+\mu )\underline{I}_{ST}-\varUpsilon \underline{I}^{2}_{ST}, \\ c\underline{I}'_{R} \le d_{R}\underline{I}''_{R}+[fr\beta _{S}(\underline{I}_{SU}+\delta \underline{I}_{ST})+\beta _{R}\underline{I}_{R}]\underline{S}-(k_{R}+\mu )\underline{I}_{R}-\varUpsilon \underline{I}^{2}_{R}. \end{array}\right. \end{aligned}$$

(43)

Proof

Choose $Q>1$ sufficiently large and $\varepsilon$ small enough such that $\xi _{3}<\xi _{2}<0$, this implies that $Q>\max \left\{ \left( \frac{\sigma }{S^{0}}\right) ^{\frac{\varepsilon }{\alpha }}, 1\right\}$.

When $\xi >\xi _{3}$, based on the definition of the lower solutions in (39), we have $\underline{I}_{SU}(\xi )=\underline{I}_{ST}(\xi )=\underline{I}_{R}(\xi )=0$. It is clear that inequalities (43) hold.

When $\xi <\xi _{3}$, by (39), we have $(\underline{I}_{SU}(\xi ), \underline{I}_{ST}(\xi ), \underline{I}_{R}(\xi ))=(\kappa _{2}, \kappa _{3}, \kappa _{4})e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi })$ and $\underline{S}(\xi )=S^{0}-\sigma e^{\alpha \xi }$. For the first inequality of (43), we can show

$$\begin{aligned}&c\underline{I}'_{SU}-d_{SU}\underline{I}''_{SU}-(1-f)\beta _{S}(\underline{I}_{SU}+\delta \underline{I}_{ST})\underline{S}+(k_{U}+\mu )\underline{I}_{SU}+\varUpsilon \underline{I}^{2}_{SU} \\&\quad =e^{\lambda _{c}\xi }\{c\kappa _{2}[\lambda _{c}(1-Qe^{\varepsilon \xi })-Q\varepsilon e^{\varepsilon \xi }]-d_{SU}\kappa _{2}\\&\qquad [\lambda ^{2}_{c}(1-Qe^{\varepsilon \xi })-\lambda _{c}Q\varepsilon e^{\varepsilon \xi }-(\lambda _{c}+\varepsilon )Q\varepsilon e^{\varepsilon \xi }] \} \\&\qquad -(1-f)\beta _{S}(\kappa _{2}+\delta \kappa _{3})e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi })(S^{0}-\sigma e^{\alpha \xi })+(k_{U}+\mu )\kappa _{2}e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi }) \\&\qquad +\varUpsilon [\kappa _{2}e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi })]^{2} \\&\quad =e^{\lambda _{c}\xi }(1-Qe^{\varepsilon \xi })\{[-d_{SU}\lambda ^{2}_{c}+c\lambda _{c}-(1-f)\beta _{S}S^{0}+k_{U}+\mu ]\kappa _{2}-(1-f)\beta _{S}\delta S^{0}\kappa _{3}\} \\&\qquad +e^{(\lambda _{c}+\varepsilon )\xi }\{[(2\lambda _{c}+\varepsilon )d_{SU}-c]Q\varepsilon \kappa _{2}+(1-f)\beta _{S}(\kappa _{2}+\delta \kappa _{3})\sigma e^{(\alpha -\varepsilon )\xi }(1-Qe^{\varepsilon \xi }) \\&\qquad +\varUpsilon \kappa ^{2}_{2}e^{(\lambda _{c}-\varepsilon )\xi }(1-Qe^{\varepsilon \xi })^{2}\} \\&\quad =e^{(\lambda _{c}+\varepsilon )\xi }\{[(2\lambda _{c}+\varepsilon )d_{SU}-c]Q\varepsilon \kappa _{2}+(1-f)\beta _{S}(\kappa _{2}+\delta \kappa _{3})\sigma e^{(\alpha -\varepsilon )\xi }(1-Qe^{\varepsilon \xi }) \\&\qquad +\varUpsilon \kappa ^{2}_{2}e^{(\lambda _{c}-\varepsilon )\xi }(1-Qe^{\varepsilon \xi })^{2}\} \\&\quad \le e^{(\lambda _{c}+\varepsilon )\xi }\Big \{[(2\lambda _{c}+\varepsilon )d_{SU}-c]Q\varepsilon \kappa _{2} \\&\qquad +(1-f)\beta _{S}(\kappa _{2}+\delta \kappa _{3})\sigma e^{-(\alpha -\varepsilon )\frac{\ln Q}{\varepsilon }}+\varUpsilon \kappa ^{2}_{2}e^{-(\lambda _{c}-\varepsilon )\frac{\ln Q}{\varepsilon }}\Big \}. \end{aligned}$$

In view of the conditions that $\varepsilon >0$ and $\lambda _{c}+\varepsilon <\frac{c}{2d}$, we have

$$\begin{aligned} (2\lambda _{c}+\varepsilon )d_{SU}-c<2(\lambda _{c}+\varepsilon )d_{SU}-c<2(\lambda _{c}+\varepsilon )d-c<0. \end{aligned}$$

Thus, we can choose sufficiently large $Q>1$ such that

$$\begin{aligned}{}[(2\lambda _{c}+\varepsilon )d_{SU}-c]Q\varepsilon \kappa _{2}+(1-f)\beta _{S}(\kappa _{2}+\delta \kappa _{3})\sigma e^{-(\alpha -\varepsilon )\frac{\ln Q}{\varepsilon }}+\varUpsilon \kappa ^{2}_{2}e^{-(\lambda _{c}-\varepsilon )\frac{\ln Q}{\varepsilon }}\le 0, \end{aligned}$$

indicating that the first inequality of (43) holds. Similarly, we can verify the second and third inequalities of (43) also hold. This completes the proof. $\square$

1.4 The Existence of Semi-traveling Waves

We look for semi-traveling waves of the auxiliary system (35) in the following profile set

$$\begin{aligned} \mathfrak {L}&=\{(S(\cdot ), I_{SU}(\cdot ), I_{ST}(\cdot ), I_{R}(\cdot ))\in C_{\nu }({\mathbf {R}}, {\mathbf {R}}^{4})\nonumber \\&:\underline{S}(\xi )\le S(\xi )\le \bar{S}(\xi ), \underline{I}_{j}(\xi )\le I_{j}(\xi )\le \bar{I}_{j}(\xi ),~j=SU, ST, R,~\text {for all}~\xi \in {\mathbf {R}}\}. \end{aligned}$$

(44)

Note that $C_{\nu }({\mathbf {R}}, {\mathbf {R}}^{4})$ is a Banach space with the norm $\Vert \cdot \Vert$ formulated by

$$\begin{aligned} \Vert \varPhi \Vert :=|\varPhi (\cdot )|_{\nu }=\max \left\{ \sup _{\xi \in {\mathbf {R}}}|\varphi _{i}(\xi )|e^{-\nu |\xi |},\quad i=S, SU, ST, R\right\} , \end{aligned}$$

(45)

where $\varPhi (\xi )=(\varphi _{1}(\xi ), \varphi _{2}(\xi ), \varphi _{3}(\xi ), \varphi _{4}(\xi ))\in C_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$, $\nu$ is a positive constant which will be determined later. Obviously, $\mathfrak {L}$ is a bounded nonempty closed convex subset of $C_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$.

$C_{\nu }({\mathbf {R}},{\mathbf {R}})$ is a Banach space with the sup norm $|\varphi (\cdot )|_{\nu }:=\sup _{\xi \in {\mathbf {R}}}|\varphi (\xi )|e^{-\nu |\xi |}$, where $\varphi (\xi )\in C_{\nu }({\mathbf {R}},{\mathbf {R}})$. Let $T_{i}: \mathfrak {L}\rightarrow C_{\nu }({\mathbf {R}},{\mathbf {R}}),\,i=S, SU, ST, R$ be operators defined by

$$\begin{aligned} T_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi )&:=\vartheta _{S}S(\xi )+\varLambda -\mu S(\xi )\\&\quad -[\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )]S(\xi ),\\ T_{SU}(S, I_{SU}, I_{ST}, I_{R})(\xi )&:=\vartheta _{SU}I_{SU}(\xi )+(1-f)\beta _{S}(I_{SU}(\xi )\\&\quad +\delta I_{ST}(\xi ))S(\xi )-(k_{U}+\mu )I_{SU}(\xi )-\varUpsilon I^{2}_{SU}(\xi ),\\ T_{ST}(S, I_{SU}, I_{ST}, I_{R})(\xi )&:=\vartheta _{ST}I_{ST}(\xi )+f(1-r)\beta _{S}(I_{SU}(\xi )\\&\quad +\delta I_{ST}(\xi ))S(\xi )-(k_{T}+\mu )I_{ST}(\xi )-\varUpsilon I^{2}_{ST}(\xi ),\\ T_{R}(S, I_{SU}, I_{ST}, I_{R})(\xi )&:=\vartheta _{R}I_{R}(\xi )+[fr\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )]S(\xi )\\&\quad -(k_{R}+\mu )I_{R}(\xi )-\varUpsilon I^{2}_{R}(\xi ), \end{aligned}$$

where

$$\begin{aligned}&\vartheta _{S}>\mu +[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]K^{*}, \vartheta _{SU}>2\varUpsilon \kappa _{2}K^{*}+(k_{U}+\mu ),\\&\quad \vartheta _{ST}>2\varUpsilon \kappa _{3}K^{*}+(k_{T}+\mu ), \quad \vartheta _{R}>2\varUpsilon \kappa _{4}K^{*}+(k_{R}+\mu ). \end{aligned}$$

Then, the auxiliary system (35) can be now rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} -d_{S}S''(\xi )+cS'(\xi )+\vartheta _{S}S(\xi ) = T_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi ), \\ -d_{SU}I''_{SU}(\xi )+cI'_{SU}(\xi )+\vartheta _{SU}I_{SU}(\xi ) = T_{SU}(S, I_{SU}, I_{ST}, I_{R})(\xi ), \\ -d_{ST}I''_{ST}(\xi )+cI'_{ST}(\xi )+\vartheta _{ST}I_{ST}(\xi ) = T_{ST}(S, I_{SU}, I_{ST}, I_{R})(\xi ), \\ -d_{R}I''_{R}(\xi )+cI'_{R}(\xi )+\vartheta _{R}I_{R}(\xi ) = T_{R}(S, I_{SU}, I_{ST}, I_{R})(\xi ). \end{array}\right. \end{aligned}$$

(46)

Let $\zeta _{i1}<0<\zeta _{i2}$ be the roots of the quadratic equation $d_{i}\zeta _{i}^{2}-c\zeta _{i}-\vartheta _{i}=0,$ then define the operators $G_{i}: \mathfrak {L}\rightarrow C_{\nu }({\mathbf {R}},{\mathbf {R}})$ by

$$\begin{aligned} G_{i}(S, I_{SU}, I_{ST}, I_{R})(\xi )&:= \frac{1}{d_{i}\zeta _{i}} \left[ \displaystyle \int ^{\xi }_{-\infty }e^{\zeta _{i1}(\xi -s)}T_{i}(S, I_{SU}, I_{ST}, I_{R})(s)\mathrm{d}s\right. \\&\quad \left. +\displaystyle \int ^{+\infty }_{\xi }e^{\zeta _{i2}(\xi -s)}T_{i}(S, I_{SU}, I_{ST}, I_{R})(s)\mathrm{d}s\right] , \end{aligned}$$

where $\zeta _{i} = \zeta _{i2}-\zeta _{i1},\,i = S, SU, ST, R$. Then, $G=(G_{S}, G_{SU}, G_{ST}, G_{R}): \mathfrak {L}\rightarrow C_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$ is a well-defined map and satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} -d_{S}G_{S}''(\xi )+cG_{S}'(\xi )+\vartheta _{S}G_{S}(\xi ) = T_{S}(G_{S}, G_{SU}, G_{ST}, G_{R})(\xi ), \\ -d_{SU}G''_{SU}(\xi )+cG'_{SU}(\xi )+\vartheta _{SU}G_{SU}(\xi ) = T_{SU}(G_{S}, G_{SU}, G_{ST}, G_{R})(\xi ), \\ -d_{ST}G''_{ST}(\xi )+cG'_{ST}(\xi )+\vartheta _{ST}G_{ST}(\xi ) = T_{ST}(G_{S}, G_{SU}, G_{ST}, G_{R})(\xi ), \\ -d_{R}G''_{R}(\xi )+cG'_{R}(\xi )+\vartheta _{R}G_{R}(\xi ) = T_{R}(G_{S}, G_{SU}, G_{ST}, G_{R})(\xi ), \end{array}\right. \end{aligned}$$

for any $(S(\cdot ), I_{SU}(\cdot ), I_{ST}(\cdot ), I_{R}(\cdot ))\in C_{\nu }({\mathbf {R}}, {\mathbf {R}}^{4})$. Thus, any fixed point of the operator G is a solution of (46), which is a traveling wave of the auxiliary system (35). On the other hand, a solution of (46) is also a fixed point of the operator G.

To apply Schauder’s fixed-point theorem, we need to prove that the operators $G_{S}, G_{SU}$, $G_{ST}$ and $G_{R}$ admit the following properties:

Lemma A.6

The operator G maps $\mathfrak {L}$ into $\mathfrak {L}$, i.e., $G(\mathfrak {L})\subset \mathfrak {L}$.

Proof

If $(S(\cdot ), I_{SU}(\cdot ), I_{ST}(\cdot ), I_{R}(\cdot ))\in \mathfrak {L}$, that is,

$$\begin{aligned} \underline{S}(\xi ) \le S(\xi )\le \bar{S}(\xi )=S^{0},\quad \underline{I}_{i}(\xi )\le I_{i}(\xi )\le \bar{I}_{i}(\xi ),\quad i=SU,ST,R \end{aligned}$$

for any $\xi \in {\mathbf {R}}$. Then, it suffices to show

$$\begin{aligned}\begin{array}{l} \underline{S}(\xi ) \le G_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi )\le \bar{S}(\xi )=S^{0}, \\ \underline{I}_{i}(\xi ) \le G_{i}(S, I_{SU}, I_{ST}, I_{R})(\xi )\le \bar{I}_{i}(\xi ),\quad i=SU,ST,R. \end{array} \end{aligned}$$

We now prove the first inequality about the operator $G_{S}$. First consider the left-hand side of the first inequality.

If $\xi \ge \xi _{2}$, then $\underline{S}(\xi ) = 0$ by (39). Based on the choice of $\vartheta _{S}$, it is obvious that

$$\begin{aligned} T_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi )\ge 0 \end{aligned}$$

for all $\xi \in {\mathbf {R}}$, which implies that $G_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi )\ge 0=\underline{S}(\xi )$ when $\xi \ge \xi _{2}$.

If $\xi <\xi _{2}$, then by Lemma A.4, we obtain

$$\begin{aligned}&-d_{S}\underline{S}''(\xi )+c\underline{S}'(\xi )+\vartheta _{S}\underline{S}(\xi ) \\&\qquad \le \vartheta _{S}\underline{S}(\xi )+\varLambda -\mu \underline{S}(\xi )-[\beta _{S}(\bar{I}_{SU}(\xi )+\delta \bar{I}_{ST}(\xi ))+\beta _{R}\bar{I}_{R}(\xi )]\underline{S}(\xi ) \\&\qquad = \{\vartheta _{S}-\mu -[\beta _{S}(\bar{I}_{SU}(\xi )+\delta \bar{I}_{ST}(\xi ))+\beta _{R}\bar{I}_{R}(\xi )]\}\underline{S}(\xi )+\varLambda \\&\qquad \le \{\vartheta _{S}-\mu -[\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )]\}S(\xi )+\varLambda \\&\qquad = T_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi ), \end{aligned}$$

which follows

$$\begin{aligned}&G_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi ) \\&\quad =\frac{1}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] T_{S}(S, I_{SU}, I_{ST}, I_{R})(s)\mathrm{d}s \\&\quad \ge \frac{1}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] [-d_{S}\underline{S}''(s)+c\underline{S}'(s)+\vartheta _{S}\underline{S}(s)]\mathrm{d}s \\&\quad =\frac{1}{d_{S}\zeta _{S}}\int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}[-d_{S}\underline{S}''(s)+c\underline{S}'(s)+\vartheta _{S}\underline{S}(s)]\mathrm{d}s \\&\qquad +\frac{1}{d_{S}\zeta _{S}}\int ^{\xi _{2}}_{\xi }e^{\zeta _{S2}(\xi -s)}[-d_{S}\underline{S}''(s)+c\underline{S}'(s)+\vartheta _{S}\underline{S}(s)]\mathrm{d}s \\&\qquad +\frac{1}{d_{S}\zeta _{S}}\int ^{+\infty }_{\xi _{2}}e^{\zeta _{S2}(\xi -s)}[-d_{S}\underline{S}''(s)+c\underline{S}'(s)+\vartheta _{S}\underline{S}(s)]\mathrm{d}s \\&\quad =\underline{S}(\xi )+\frac{1}{\zeta _{S}}e^{\zeta _{S2}(\xi -\xi _{2})}[\underline{S}'(\xi _{2}+0)-\underline{S}'(\xi _{2}-0)] \\&\quad \ge \underline{S}(\xi ), \end{aligned}$$

where the final inequality uses the fact that $\underline{S}'(\xi _{2}+0)=0$ and $\underline{S}'(\xi _{2}-0)<0$.

To summarize, $G_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi )\ge \underline{S}(\xi )$ for all $\xi \in {\mathbf {R}}$.

Next, we prove the right-hand side of the first inequality, i.e., $G_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi ) \le$ $\bar{S}(\xi )=S^{0}$, for all $\xi \in {\mathbf {R}}$.

It is easy to verify the validity of the following inequality for all $\xi \in {\mathbf {R}}$

$$\begin{aligned} c\bar{S}'(\xi )\ge d_{S}\bar{S}''(\xi )+\varLambda -\mu \bar{S}(\xi )-[\beta _{S}(\underline{I}_{SU}(\xi )+\delta \underline{I}_{ST}(\xi ))+\beta _{R}\underline{I}_{R}(\xi )]\bar{S}(\xi ), \end{aligned}$$

it follows that

$$\begin{aligned}&-d_{S}\bar{S}''(\xi )+c\bar{S}'(\xi )+\vartheta _{S}\bar{S}(\xi ) \\&\qquad \ge \vartheta _{S}\bar{S}(\xi )+\varLambda -\mu \bar{S}(\xi )-[\beta _{S}(\underline{I}_{SU}(\xi )+\delta \underline{I}_{ST}(\xi ))+\beta _{R}\underline{I}_{R}(\xi )]\bar{S}(\xi ) \\&\qquad = \{\vartheta _{S}-\mu -[\beta _{S}(\underline{I}_{SU}(\xi )+\delta \underline{I}_{ST}(\xi ))+\beta _{R}\underline{I}_{R}(\xi )]\}\bar{S}(\xi )+\varLambda \\&\qquad \ge \{\vartheta _{S}-\mu -[\beta _{S}(I_{SU}(\xi )+\delta I_{ST}(\xi ))+\beta _{R}I_{R}(\xi )]\}S(\xi )+\varLambda \\&\qquad = T_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi ). \end{aligned}$$

Through the above inequality, we can prove that, for all $\xi \in {\mathbf {R}}$,

$$\begin{aligned}&G_{S}(S, I_{SU}, I_{ST}, I_{R})(\xi ) \\&\quad =\frac{1}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] T_{S}(S, I_{SU}, I_{ST}, I_{R})(s)\mathrm{d}s \\&\quad \le \frac{1}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] [-d_{S}\bar{S}''(s)+c\bar{S}'(s)+\vartheta _{S}\bar{S}(s)]\mathrm{d}s \\&\quad =\frac{1}{d_{S}\zeta _{S}}\int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}[-d_{S}\bar{S}''(s)+c\bar{S}'(s)+\vartheta _{S}\bar{S}(s)]\mathrm{d}s \\&\qquad +\frac{1}{d_{S}\zeta _{S}}\int ^{\xi }_{+\infty }e^{\zeta _{S2}(\xi -s)}[-d_{S}\bar{S}''(s)+c\bar{S}'(s)+\vartheta _{S}\bar{S}(s)]\mathrm{d}s \\&\quad =\bar{S}(\xi ). \end{aligned}$$

In a similar way, we can also show that the remaining three inequalities about operators $G_{i},\,i=SU,ST,R$ hold for any $\xi \in {\mathbf {R}}$. Thus, we complete the proof of the lemma. $\square$

In what follows, we shall apply Schauder’s fixed-point theorem to the operator G, which requires the continuity and compactness of G. To achieve the two properties, we need to introduce a topology in $C_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$. Let $\nu \in (0, \min \{-\zeta _{i1}, \zeta _{i2},\,i=S,SU,ST,R\})$. Denote

$$\begin{aligned} B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})=\{\varPhi (\xi ) = (\varphi _{1}(\xi ), \varphi _{2}(\xi ), \varphi _{3}(\xi ), \varphi _{4}(\xi ))\in C_{\nu }({\mathbf {R}},{\mathbf {R}}^{4}): |\varPhi (\cdot )|_{\nu }<+\infty \} \end{aligned}$$

with the same norm as that in (45), then it is easy to verify that $(B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4}), |\cdot |_{\nu })$ is a Banach space.

Lemma A.7

The operator $G=(G_{S}, G_{SU}, G_{ST}, G_{R}): \mathfrak {L}\rightarrow \mathfrak {L}$ is continuous with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$.

Proof

For $\varPhi (\xi ) = (\varphi _{1}(\xi ), \varphi _{2}(\xi ), \varphi _{3}(\xi ), \varphi _{4}(\xi )), \varPsi (\xi ) = (\psi _{1}(\xi ), \psi _{2}(\xi ), \psi _{3}(\xi ), \psi _{4}(\xi ))\in \mathfrak {L}$, by the definition of the operator $T_{S}$, we easily get

$$\begin{aligned}&|T_{S}(\varPhi )(\xi )-T_{S}(\varPsi )(\xi )|e^{-\nu |\xi |} \\&\quad =|\{\vartheta _{S}-\mu -[\beta _{S}(\varphi _{2}(\xi )+\delta \varphi _{3}(\xi ))+\beta _{R}\varphi _{4}(\xi )]\}(\varphi _{1}(\xi )-\psi _{1}(\xi )) \\&\qquad +\psi _{1}(\xi )\{\beta _{S}[(\psi _{2}(\xi )-\varphi _{2}(\xi ))+\delta (\psi _{3}(\xi )-\varphi _{3}(\xi ))] +\beta _{R}(\psi _{4}(\xi )-\varphi _{4}(\xi ))\}|e^{-\nu |\xi |} \\&\quad \le N_{S}|\varPhi (\cdot )-\varPsi (\cdot )|_{\nu }, \end{aligned}$$

where $N_{S}=\vartheta _{S}-\mu -[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]K^{*}+[\beta _{S}(1+\delta )+\beta _{R}]S^{0}>0$. Then, by the definition of the operator $G_{S}$, we obtain

$$\begin{aligned}&|G_{S}(\varPhi )(\xi )-G_{S}(\varPsi )(\xi )|e^{-\nu |\xi |} \\&\quad \le \frac{e^{-\nu |\xi |}}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] |T_{S}(\varPhi )(s)-T_{S}(\varPsi )(s)|\mathrm{d}s \\&\quad \le \frac{N_{S}e^{-\nu |\xi |}}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)+\nu |s|}\mathrm{d}s+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)+\nu |s|}\mathrm{d}s\right] |\varPhi (\cdot )-\varPsi (\cdot )|_{\nu } \\&\quad =\frac{N_{S}}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)-\nu |\xi |+\nu |s|}\mathrm{d}s+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)-\nu |\xi |+\nu |s|}\mathrm{d}s\right] |\varPhi (\cdot )-\varPsi (\cdot )|_{\nu } \\&\quad \le \frac{N_{S}}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)+\nu |\xi -s|}\mathrm{d}s+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)+\nu |\xi -s|}\mathrm{d}s\right] |\varPhi (\cdot )-\varPsi (\cdot )|_{\nu } \\&\quad =\frac{N_{S}}{d_{S}\zeta _{S}}\frac{\zeta _{S1}-\zeta _{S2}+2\nu }{(\zeta _{S1}+\nu )(\zeta _{S2}-\nu )}|\varPhi (\cdot )-\varPsi (\cdot )|_{\nu }. \end{aligned}$$

Hence, $G_{S}: \mathfrak {L}\rightarrow C_{\nu }({\mathbf {R}},{\mathbf {R}})$ is continuous with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}})$. Similarly, we can show the remaining operators $G_{i}: \mathfrak {L}\rightarrow C_{\nu }({\mathbf {R}},{\mathbf {R}}),\;i=SU, ST, R$ are also continuous with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}})$. This implies that $G: \mathfrak {L}\rightarrow \mathfrak {L}$ is continuous with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$. The proof is completed. $\square$

Lemma A.8

The operator $G=(G_{S}, G_{SU}, G_{ST}, G_{R}): \mathfrak {L}\rightarrow \mathfrak {L}$ is compact with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$.

Proof

Let $\varPhi (\xi ) = (\varphi _{1}(\xi ), \varphi _{2}(\xi ), \varphi _{3}(\xi ), \varphi _{4}(\xi ))\in \mathfrak {L}$, obviously, for all $\xi \in {\mathbf {R}}$, we have

$$\begin{aligned} |T_{S}(\varPhi )(\xi )|=|\vartheta _{S}\varphi _{1}(\xi )+\varLambda -\mu \varphi _{1}(\xi )-[\beta _{S}(\varphi _{2}(\xi )+\delta \varphi _{3}(\xi ))+\beta _{R}\varphi _{4}(\xi )]\varphi _{1}(\xi )|\le \tilde{N}_{S}, \end{aligned}$$

where $\tilde{N}_{S}=\varLambda +\{\vartheta _{S}+\mu +[\beta _{S}(\kappa _{2}+\delta \kappa _{3})+\beta _{R}\kappa _{4}]K^{*}\}S^{0}$.

Consequently,

$$\begin{aligned} \left| \frac{d}{\mathrm{d}\xi }G_{S}(\varPhi )(\xi )\right|&=\frac{1}{d_{S}\zeta _{S}}\left| \left[ \zeta _{S1}\int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\zeta _{S2}\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] T_{S}(\varPhi )(s)\mathrm{d}s\right| \\&\le \frac{\tilde{N}_{S}}{d_{S}\zeta _{S}}\left[ |\zeta _{S1}|\int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}\mathrm{d}s+\zeta _{S2}\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\mathrm{d}s\right] \\&=\frac{2\tilde{N}_{S}}{d_{S}\zeta _{S}}, \end{aligned}$$

which implies $\left| \frac{d}{\mathrm{d}\xi }G_{S}(\varPhi )(\cdot )\right| _{\nu }<\frac{2\tilde{N}_{S}}{d_{S}\zeta _{S}}.$ So, we see that $|\frac{d}{\mathrm{d}\xi }G_{S}(\varPhi )(\xi )|_{\nu }$ is bounded. Using similar arguments as above, we can show that $|\frac{d}{\mathrm{d}\xi }G_{i}(\varPhi )(\xi )|_{\nu },\,i=SU,ST,R$ are also bounded. This means that $G(\mathfrak {L})$ is uniformly bounded and equicontinuous with respect to the norm $|\cdot |_{\nu }$.

For fixed positive integer n, we define an operator $G^{n} = (G_{S}^{n}, G_{SU}^{n}, G_{ST}^{n}, G_{R}^{n})$ by

$$\begin{aligned} G^{n}(\varPhi )(\xi )=\left\{ \begin{array}{ll} G(\varPhi )(-n), &{}\quad \xi \in (-\infty ,-n], \\ G(\varPhi )(\xi ), &{}\quad \xi \in [-n,n], \\ G(\varPhi )(n), &{}\quad \xi \in [n,+\infty ). \end{array}\right. \end{aligned}$$

By Arzelà–Ascoli theorem, $G^{n}: \mathfrak {L}\rightarrow \mathfrak {L}$ is compact with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$. Since

$$\begin{aligned} |G_{S}(\varPhi )(\xi )|&=\frac{1}{d_{S}\zeta _{S}}\left| \left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\right] T_{S}(\varPhi )(s)\mathrm{d}s\right| \\&\le \frac{\tilde{N}_{S}}{d_{S}\zeta _{S}}\left[ \int ^{\xi }_{-\infty }e^{\zeta _{S1}(\xi -s)}\mathrm{d}s+\int ^{+\infty }_{\xi }e^{\zeta _{S2}(\xi -s)}\mathrm{d}s\right] = \frac{\tilde{N}_{S}}{d_{S}|\zeta _{S1}|\zeta _{S2}}, \end{aligned}$$

we have

$$\begin{aligned} |G^{n}_{S}(\varPhi )(\cdot )-G_{S}(\varPhi )(\cdot )|_{\nu }&=\sup _{\xi \in {\mathbf {R}}}|G^{n}_{S}(\varPhi )(\xi )-G_{S}(\varPhi )(\xi )|e^{-\nu |\xi |} \\&=\displaystyle \sup _{|\xi |\ge n}|G^{n}_{S}(\varPhi (\cdot ))(\xi )-G_{S}(\varPhi (\cdot ))(\xi )|e^{-\nu |\xi |} \le \frac{2\tilde{N}_{S}}{d_{S}|\zeta _{S1}|\zeta _{S2}}e^{-\nu n}. \end{aligned}$$

When $n\rightarrow +\infty$, we have $|G^{n}_{S}(\varPhi )(\cdot )-G_{S}(\varPhi )(\cdot )|_{\nu }\rightarrow 0$. By similar arguments, we can also show that $|G^{n}_{i}(\varPhi )(\cdot )-G_{i}(\varPhi )(\cdot )|_{\nu }\rightarrow 0$ when $n\rightarrow +\infty$ for $i=SU, ST, R$.

Overall, $|G^{n}(\varPhi )(\cdot )-G(\varPhi )(\cdot )|_{\nu }\rightarrow 0$ when $n\rightarrow +\infty$. By Proposition 2.12 in Zeilder (1986), we know that $G^{n}$ converges to G in $\mathfrak {L}$ with respect to the norm $|\cdot |_{\nu }$. Therefore, the operator $G=(G_{S}, G_{SU}, G_{ST}, G_{R}): \mathfrak {L}\rightarrow \mathfrak {L}$ is compact with respect to the norm $|\cdot |_{\nu }$ in $B_{\nu }({\mathbf {R}},{\mathbf {R}}^{4})$. This completes the proof. $\square$

Lemmas B.1 and B.2

Lemma B.1

Let X be locally compact, and let $X_{2}$ be compact in X and $X_{1}$ be forward invariant under the continuous semiflow $\varPhi$ on X. Assume that $\varOmega _{2}$, defined by

$$\begin{aligned} \varOmega _{2}=\bigcup _{y\in Y_{2}}\omega (y),\quad Y_{2}=\{x\in X_{2}:\varPhi _{t}(x)\in X_{2}, \forall t>0\}, \end{aligned}$$

has an acyclic isolated covering $M=\bigcup _{k=1}^{m}M_{k}$. If each part $M_{k}$ of M is a weak repeller for $X_{1}$, then $X_{2}$ is a uniform strong repeller for $X_{1}$.

Lemma B.2

If $R_{SC}>1>R_{RC}$ (defined in (7) and (8)), and $c>\max \{c^{*}, \tilde{c}^{*}\}$ $(c^{*}>0$ is defined by Lemma A.1, $\tilde{c}^{*}>\max \{2\sqrt{d_{SU}P_{SU}(0)}, 2\sqrt{d_{ST}P_{ST}(0)}\})$ hold. Let $W^{s}(E^{0})$ denote the stable manifold of system (16) at the equilibrium $E^{0}$, then we have

$$\begin{aligned} W^{s}(E^{0})\cap X_{1}=\emptyset , \end{aligned}$$

where $E^{0}=(S^{0}, 0, 0, 0, 0, 0, 0, 0)$ and $\emptyset$ denotes the empty set.

Proof

First, we calculate the Jacobian matrix of system (16) at $E^{0}$ as follows:

$$\begin{aligned} J= \left( \begin{array}{cccccccc} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{\mu }{d_{S}} &{} \frac{c}{d_{S}} &{} \frac{\beta _{S}S^{0}}{d_{S}} &{} 0 &{} \frac{\beta _{S}\delta S^{0}}{d_{S}} &{} 0 &{} \frac{\beta _{R}S^{0}}{d_{S}} &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{k_{U}+\mu -(1-f)\beta _{S}S^{0}}{d_{SU}} &{} \frac{c}{d_{SU}} &{} \frac{-(1-f)\beta _{S}\delta S^{0}}{d_{SU}} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} \frac{-f(1-r)\beta _{S}S^{0}}{d_{ST}} &{} 0 &{} \frac{k_{T}+\mu -f(1-r)\beta _{S}\delta S^{0}}{d_{ST}} &{} \frac{c}{d_{ST}} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} \frac{-fr\beta _{S}S^{0}}{d_{R}} &{} 0 &{} \frac{-fr\beta _{S}\delta S^{0}}{d_{R}} &{} 0 &{} \frac{k_{R}+\mu -\beta _{R}S^{0}}{d_{R}} &{} \frac{c}{d_{R}} \\ \end{array} \right) . \end{aligned}$$

Let

$$\begin{aligned} J_{11}&=\left( \begin{array}{cc} 0 &{} 1 \\ \frac{\mu }{d_{S}} &{} \frac{c}{d_{S}} \\ \end{array} \right) ,\quad J_{33}=\left( \begin{array}{cc} 0 &{} 1 \\ \frac{k_{R}+\mu -\beta _{R}S^{0}}{d_{R}} &{} \frac{c}{d_{R}} \\ \end{array} \right) ,\\ J_{22}&=\left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0 \\ \frac{k_{U}+\mu -(1-f)\beta _{S}S^{0}}{d_{SU}} &{} \frac{c}{d_{SU}} &{} \frac{-(1-f)\beta _{S}\delta S^{0}}{d_{SU}} &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ \frac{-f(1-r)\beta _{S}S^{0}}{d_{ST}} &{} 0 &{} \frac{k_{T}+\mu -f(1-r)\beta _{S}\delta S^{0}}{d_{ST}} &{} \frac{c}{d_{ST}} \\ \end{array} \right) . \end{aligned}$$

Obviously, the characteristic polynomial of J will be determined by the characteristic polynomial of $J_{11}, J_{22}$ and $J_{33}$. That is to say, the eigenvalues of J consist of the eigenvalues of $J_{11}, J_{22}$ and $J_{33}$, so we consider the characteristic equations of $J_{11}, J_{22}$ and $J_{33}$ and calculate their eigenvalues, respectively.

Upon a direct computation, one is able to verify that $J_{11}$ and $J_{33}$ have eigenvalues

$$\begin{aligned} \lambda ^{\pm }_{11}=\frac{c\pm \sqrt{c^{2}+4d_{S}\mu }}{2d_{S}},\quad \lambda ^{\pm }_{33}=\frac{c\pm \sqrt{c^{2}+4d_{R}(k_{R}+\mu )(1-R_{RC})}}{2d_{R}}. \end{aligned}$$

$J_{11}$ has one positive eigenvalue $\lambda ^{+}_{11}$ and a negative eigenvalue $\lambda ^{-}_{11}$, the eigenvector of matrix J corresponding to the negative eigenvalue $\lambda ^{-}_{11}$ is $(1, \lambda ^{-}_{11}, 0, 0, 0, 0, 0, 0)^{T}$. When $R_{RC}<1$, $J_{33}$ has one positive eigenvalue $\lambda ^{+}_{33}$ and a negative eigenvalue $\lambda ^{-}_{33}$, the corresponding eigenvector to $\lambda ^{-}_{33}$ is $(0, 0, 0, 0, 0, 0, 1, \lambda ^{-}_{33})^{T}$.

In addition, the characteristic equation of $J_{22}$ is $H(\lambda ):=P_{SU}(\lambda )P_{ST}(\lambda )-\gamma =0,$ where $P_{SU}(\lambda )=d_{SU}\lambda ^{2}-c\lambda +(1-f)\beta _{S}S^{0}-(k_{U}+\mu )$,

$P_{ST}(\lambda )=d_{ST}\lambda ^{2}-c\lambda +f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )$ and $\gamma =(1-f)\beta _{S}^2\delta f(1-r)(S^{0})^2$.

It is easy to verify that $R_{SC}>1$ if and only if $\mathfrak {A}(S^{0})<0$, where $\mathfrak {A}(S^{0})=H(0)$. From Lemma 2.1 (e) in Zhang (2017), it follows that when $c\ge \tilde{c}^{*}>\max (2\sqrt{d_{SU}P_{SU}(0)}$, $2\sqrt{d_{ST}P_{ST}(0)})$, $J_{22}$ has only one negative eigenvalue, denote by $\lambda ^{-}_{22}$. Suppose that $\alpha =(\alpha _{1},\alpha _{2},\alpha _{3},\alpha _{4},\alpha _{5}$, $\alpha _{6}$, $\alpha _{7},\alpha _{8})^T$ is the eigenvector of matrix J corresponding to $\lambda ^{-}_{22}$, wherein $(\alpha _{3}$,$\alpha _{4}$,$\alpha _{5}$,$\alpha _{6})^T$ is the eigenvector of matrix $J_{22}$ corresponding to $\lambda ^{-}_{22}$, then the relationship among the components $\alpha _{i},\,i=3,4,5,6$ can be described by

$$\begin{aligned} \begin{array}{ll} \lambda ^{-}_{22}\alpha _{3}=\alpha _{4}, \; P_{SU}(\lambda ^{-}_{22})\alpha _{3}=-G^{0}_{23}\alpha _{5}, \; P_{ST}(\lambda ^{-}_{22})\alpha _{5}=-G^{0}_{32}\alpha _{3}, \; \lambda ^{-}_{22}\alpha _{5}=\alpha _{6}, \end{array} \end{aligned}$$

(47)

where $G^{0}_{23}=(1-f)\beta _{S}\delta S^{0}, G^{0}_{32}=f(1-r)\beta _{S}S^{0}$.

It follows from (47) that $(\alpha _{3},\alpha _{4},\alpha _{5},\alpha _{6})$ has the form

$$\begin{aligned} \left( G^{0}_{23}, \lambda ^{-}_{22}G^{0}_{23}, -P_{SU}(\lambda ^{-}_{22}), -\lambda ^{-}_{22}P_{SU}(\lambda ^{-}_{22})\right) \end{aligned}$$

or equivalent form $(G^{0}_{32}, \lambda ^{-}_{22}G^{0}_{32}, -P_{ST}(\lambda ^{-}_{22}), -\lambda ^{-}_{22}P_{ST}(\lambda ^{-}_{22}))$. From Lemma 2.1 (e) in Zhang (2017), we know that $P_{SU}(\lambda ^{-}_{22})>0$ when $R_{SC}>1$ and $c\ge \tilde{c}^{*}$. So, $\alpha _{3}$ and $\alpha _{5}$ have the opposite sign.

If $\lambda ^{-}_{11}$, $\lambda ^{-}_{22}$ and $\lambda ^{-}_{33}$ are not equal to each other, the stable subspace of the linearized system of (16) at $E^{0}$ is spanned by $(1, \lambda ^{-}_{11}, 0, 0, 0, 0, 0, 0)^T$, $\alpha$ and $(0, 0, 0, 0, 0, 0, 1, \lambda ^{-}_{33})^T$. In view of $\alpha _{3}\alpha _{5}<0$, $\lambda ^{-}_{11}<0$ and $\lambda ^{-}_{33}<0$, together with the tangency of stable manifold to the stable subspace in stable manifold theorem (Perko 2001), then we have $W^{s}(E^{0})\cap X_{1}=\emptyset$.

If only two of $\lambda ^{-}_{11}$, $\lambda ^{-}_{22}$ and $\lambda ^{-}_{33}$ are equal or all three are equal, without loss of generality, we suppose that $\lambda ^{-}_{22}=\lambda ^{-}_{11}$ or $\lambda ^{-}_{22}=\lambda ^{-}_{11}=\lambda ^{-}_{33}$. Since $\lambda ^{-}_{22}$ is a simple eigenvalue of $J_{22}$ and a multiple eigenvalue of J with multiplicity 1 or 2, then the stable subspace of the linearized system of system (16) at $E^{0}$ is spanned by $(1, \lambda ^{-}_{11}, 0, 0, 0, 0, 0, 0)^T$, $\tilde{\alpha }$ and $(0, 0, 0, 0, 0, 0, 1, \lambda ^{-}_{33})^T$, where the elements $\tilde{\alpha }_{3}$ and $\tilde{\alpha }_{5}$ of the eigenvector $\tilde{\alpha }$ satisfy $\tilde{\alpha }_{3}\tilde{\alpha }_{5}<0$ by (47). Similar to the above discussion, we can get the conclusion that $W^{s}(E^{0})\cap X_{1}=\emptyset$. Thus, the proof of the lemma is completed. $\square$

Lemmas C.1 and C.2

Lemma C.1

Suppose that $R_{C}>1$, $R_{i}\ne 1,\,i=SC,RC$ are satisfied. For any $c>0$, if $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ is a nonnegative semi-traveling wave of the diffusive model (2) satisfying the asymptotic boundary condition (13), then there exists a positive constant $\eta$ such that

$$\begin{aligned} \sup _{\xi \in {\mathbf {R}}}\{|S^{0}-S(\xi )|e^{-\eta \xi }\}<+\infty ,\quad \sup _{\xi \in {\mathbf {R}}}\{|I_{j}(\xi )|e^{-\eta \xi }\}<+\infty ,\quad j=SU,ST,R. \end{aligned}$$

(48)

Proof

Since nonnegative traveling wave $(S(\xi ), I_{SU}(\xi ), I_{ST}(\xi ), I_{R}(\xi ))$ of the diffusive model (2) satisfies the boundary condition (13), we have, as $\xi \rightarrow -\infty$,

$$\begin{aligned} (S, V_{S}, I_{SU}, V_{SU}, I_{ST}, V_{ST}, I_{R}, V_{R})(\xi )\rightarrow \bar{E}^{0}(S^{0}, 0, 0, 0, 0, 0, 0, 0). \end{aligned}$$

It is easy to calculate the characteristic polynomial of the linearized system of equivalent system (16) of wave Eq. (36) at $\bar{E}^{0}$ as follows

$$\begin{aligned} P_{S}(\lambda )H(\lambda )P_{R}(\lambda )=0, \end{aligned}$$

(49)

where $P_{R}(\lambda )=d_{R}\lambda ^{2}-c\lambda +\beta _{R}S^{0}-(k_{R}+\mu )$.

When $R_{RC}\ne 1$, we know that the roots of the polynomials $P_{S}(\lambda )=0$ and $P_{R}(\lambda )=0$ have no zero real part. Next, we determine whether the polynomial $H(\lambda )=P_{SU}(\lambda )P_{ST}(\lambda )$ $-\gamma =0$ has a eigenvalue with zero real part. Since $H(0)=P_{SU}(0)P_{ST}(0)-\gamma =(k_{U}+\mu )(k_{T}+\mu )(1-R_{SC})\ne 0$ when $R_{SC}\ne 1$, $\lambda =0$ is not the root of $H(\lambda )=0$. By $H(\lambda )=0$, we get the following quartic polynomial of $\lambda$

$$\begin{aligned} \lambda ^{4}+a_{3}\lambda ^{3}+a_{2}\lambda ^{2}+a_{1}\lambda +a_{0}=0, \end{aligned}$$

(50)

where

$$\begin{aligned} a_{3}&=-\frac{c(d_{SU}+d_{ST})}{d_{SU}d_{ST}}, \quad a_{2}=\frac{c^{2}}{d_{SU}d_{ST}}+\frac{(1-f)\beta _{S}S^{0}-(k_{U}+\mu )}{d_{SU}}\\&\quad +\frac{f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )}{d_{ST}},\\ a_{1}&=-\frac{c[f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )+(1-f)\beta _{S}S^{0}-(k_{U}+\mu )]}{d_{SU}d_{ST}},\\ a_{0}&=\frac{[(1-f)\beta _{S}S^{0}-(k_{U}+\mu )][f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )]}{d_{SU}d_{ST}}\\&\quad -\frac{(1-f)\beta _{S}\delta S^{0}f(1-r)\beta _{S}S^{0}}{d_{SU}d_{ST}}. \end{aligned}$$

Suppose that (50) has a pure imaginary root, denoted by $\lambda =\beta i, \beta \ne 0$, then we substitute $\lambda =\beta i$ into (50), yielding

$$\begin{aligned} \beta ^{4}-a_{2}\beta ^{2}+a_{0}=0,\quad a_{1}= a_{3}\beta ^{2}. \end{aligned}$$

(51)

On account of $\beta ^{2}>0$ and $a_{3}<0$, we have $a_{1}<0$, implying

$$\begin{aligned} f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )+(1-f)\beta _{S}S^{0}-(k_{U}+\mu )>0. \end{aligned}$$

Combining the two equalities in (51), we obtain

$$\begin{aligned} a^{2}_{1}+a_{0}a^{2}_{3}-a_{1}a_{2}a_{3}=0. \end{aligned}$$

(52)

Through calculations, we can get the following inequality

$$\begin{aligned}&a^{2}_{1}+a_{0}a^{2}_{3}-a_{1}a_{2}a_{3}\\&\quad =-\frac{c^{2}}{d^{3}_{SU}d^{3}_{ST}}\lfloor (d_{SU}+d_{ST})[f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )+(1-f)\beta _{S}S^{0}-(k_{U}+\mu )]c^{2} \\&\qquad +\{d_{SU}[f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu )]-d_{ST}[(1-f)\beta _{S}S^{0}-(k_{U}+\mu )]\}^{2} \\&\qquad +(1-f)\beta _{S}S^{0}f(1-r)\beta _{S}\delta S^{0}(d_{SU}+d_{ST})^{2}\rfloor \\&\quad <0,\quad \text {for}\;c>0, \end{aligned}$$

which is in contradiction with (52). Thus, when $R_{C}>1$ and $R_{i}\ne 1,\,i=SC,RC$, the characteristic polynomial (49) has no roots with zero real parts for any $c>0$, implying that the equilibrium $\bar{E}^{0}$ is hyperbolic. By using stable manifold theorem in Perko (2001), we know that there exists a positive constant $\eta$ such that (48) holds. The proof is therefore completed. $\square$

Lemma C.2

For any $c\in (0,c_{2}^{*})$, there does not exist positive real root $\lambda ^{*}$ for

$$\begin{aligned} H(\lambda )=P_{SU}(\lambda )P_{ST}(\lambda )-\gamma =0 \end{aligned}$$

such that $P_{SU}(\lambda ^{*})<0$ and $P_{ST}(\lambda ^{*})<0$, where

$$\begin{aligned} \begin{array}{l} c_{2}^{*}:=\inf _{\lambda >0}\frac{\widetilde{P}_{SU}(\lambda )+\widetilde{P}_{ST}(\lambda )+\sqrt{(\widetilde{P}_{SU}(\lambda )-\widetilde{P}_{ST}(\lambda ))^{2}+4\gamma }}{2\lambda }, \\ \widetilde{P}_{SU}(\lambda )=d_{SU}\lambda ^{2}+(1-f)\beta _{S}S^{0}-(k_{U}+\mu ),\\ \widetilde{P}_{ST}(\lambda )=d_{ST}\lambda ^{2}+f(1-r)\beta _{S}\delta S^{0}-(k_{T}+\mu ). \end{array} \end{aligned}$$

(53)

Proof

Suppose that $H(\lambda )=P_{SU}(\lambda )P_{ST}(\lambda )-\gamma =0$ has a positive real root $\lambda ^{*}$, satisfying

$$\begin{aligned} H(\lambda ^{*})=P_{SU}(\lambda ^{*})P_{ST}(\lambda ^{*})-\gamma =0, \end{aligned}$$

(54)

and $P_{SU}(\lambda ^{*})<0,~P_{ST}(\lambda ^{*})<0.$

Since $0<c<c_{2}^{*}$, by the definition of $c_{2}^{*}$ in (53), we have

$$\begin{aligned} c\lambda ^{*}<\frac{\widetilde{P}_{SU}(\lambda ^{*})+\widetilde{P}_{ST}(\lambda ^{*})+\sqrt{(\widetilde{P}_{SU}(\lambda ^{*})-\widetilde{P}_{ST}(\lambda ^{*}))^{2}+4\gamma }}{2}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} 0>P_{SU}(\lambda ^{*})&=\widetilde{P}_{SU}(\lambda ^{*})-c\lambda ^{*} \\&>\frac{\widetilde{P}_{SU}(\lambda ^{*})-\widetilde{P}_{ST}(\lambda ^{*})-\sqrt{(\widetilde{P}_{SU}(\lambda ^{*})-\widetilde{P}_{ST}(\lambda ^{*}))^{2}+4\gamma }}{2}, \end{aligned}$$

and $0>P_{ST}(\lambda ^{*})=\widetilde{P}_{ST}(\lambda ^{*})-c\lambda ^{*} >\frac{\widetilde{P}_{ST}(\lambda ^{*})-\widetilde{P}_{SU}(\lambda ^{*})-\sqrt{(\widetilde{P}_{SU}(\lambda ^{*})-\widetilde{P}_{ST}(\lambda ^{*}))^{2}+4\gamma }}{2}.$

It follows that $0<P_{SU}(\lambda ^{*})P_{ST}(\lambda ^{*})<\gamma ,$ which is in contradiction with (54). Thus, we complete the proof of the lemma. $\square$