Modeling and Dynamics Analysis of Zika Transmission with Limited Medical Resources

Abstract

Zika virus, a reemerging mosquito-borne flavivirus, posed a global public health emergency in 2016. Brazil is the most seriously affected country. Some measures have been implemented to control the Zika transmission, such as spraying mosquitoes, developing vaccines and drugs. However, because of the limited medical resources (LMRs) in the country, not every infected patient can be treated in time when infected with Zika virus. We aim to build a deterministic Zika model by introducing a piecewise smooth treatment recovery rate to research the effect of LMRs on the transmission and control of Zika. For the model without treatment, we analyze the global stability of equilibria. For the model with treatment, the model exhibits complex dynamics. We prove that the model with treatment undergoes backward bifurcation, Hopf bifurcation and Bogdanov–Takens bifurcation of codimension 2. It means that the model with LMRs is sensitive to parameters and initial conditions, which has important significance for control of Zika. We also apply the model to estimate the basic and control reproduction numbers for the Zika transmission by using the data on weekly reported accumulated Zika cases from March 25, 2016, to April 14, 2018, in Brazil.

Appendices

: Proof of Theorem 1

Proof

Consider the Lyapunov function

$$\begin{aligned} V_\mathrm{w}=\left( \frac{S_\mathrm{h}}{S_\mathrm{hw}^0}-\hbox {ln}\frac{S_\mathrm{h}}{S_\mathrm{hw}^0}-1\right) +\frac{I_\mathrm{h}}{N_\mathrm{h}}+ \frac{( r+d_\mathrm{h})(1- R _\mathrm{hhw})}{a\beta _{2}}\cdot \frac{I_\mathrm{v}}{N_\mathrm{v}} \end{aligned}$$

in $\varGamma$. if $R_{0}^{*}<1$, then $R _\mathrm{hhw}<1$. One has $V_\mathrm{w}\ge 0$, and $V_\mathrm{w}=0$ if only if $S_\mathrm{h}=S_\mathrm{hw}^0,I_\mathrm{h}=0,I_\mathrm{v}=0.$ So, $V_\mathrm{w}$ is a positive definite function. The orbital derivative of $V_\mathrm{w}$ along the solution of system (5) can be written as

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}V_\mathrm{w}}{\hbox {d}t}\big |_{(5)} =&\,\frac{1}{S_\mathrm{h}S_\mathrm{hw}^0} \left( S_\mathrm{h}-S_\mathrm{hw}^0\right) \frac{\hbox {d}S_\mathrm{h}}{\hbox {d}t}+\frac{ 1}{N_\mathrm{h}}\frac{\hbox {d}I_\mathrm{h}}{\hbox {d}t}+\frac{( r+d_\mathrm{h}-\beta _{3})}{a\beta _{2}N_\mathrm{v}}\frac{\hbox {d}I_\mathrm{v}}{\hbox {d}t}\\ =&\,\frac{1}{S_\mathrm{h}S_\mathrm{hw}^0} (S_\mathrm{h}-S_\mathrm{hw}^0 )\left( \varLambda _\mathrm{h}-\frac{a\beta _{1}S_\mathrm{h}I_\mathrm{v}}{N_\mathrm{h}}-\beta _{3}\frac{I_\mathrm{h}S_\mathrm{h}}{N_\mathrm{h}}-d_\mathrm{h}S_\mathrm{h}\right) \\&+\,\frac{1}{N_\mathrm{h}}\left( \frac{a\beta _{1}S_\mathrm{h}I_\mathrm{v}}{N_\mathrm{h}}+\beta _{3}\frac{I_\mathrm{h}S_\mathrm{h}}{N_\mathrm{h}}-( r+d_\mathrm{h})I_\mathrm{h} \right) \\&+\,\frac{( r+d_\mathrm{h}-\beta _{3})}{a\beta _{2}N_\mathrm{v}}\left( a\beta _{2}\frac{I_\mathrm{h}(N_\mathrm{v}-I_\mathrm{v})}{N_\mathrm{h}}-d_\mathrm{v}I_\mathrm{v}\right) \\ =&\, -\frac{d_\mathrm{h}}{S_\mathrm{h}S_\mathrm{hw}^0}(S_\mathrm{hw}^0-S_\mathrm{h})^{2}-(1- R _\mathrm{hhw})\frac{( r+d_\mathrm{h})}{N_\mathrm{v}N_\mathrm{h}}I_\mathrm{v}I_\mathrm{h}\\&-\,(1- R ^{*}_\mathrm{0w})\frac{d_\mathrm{v}( r+d_\mathrm{h})}{a\beta _{2}N_\mathrm{v}}I_\mathrm{v}.\\ \end{aligned} \end{aligned}$$

If $R_{0}^{*}<1$, then $\frac{\hbox {d}V_\mathrm{w}}{\hbox {d}t}\big |_{(5)}\le 0$. So, $E_\mathrm{0w}$ is stable. It is easy to see that $E_\mathrm{0w}$ is the largest positively invariant set contained in $\frac{\hbox {d}V_\mathrm{w}}{\hbox {d}t}\big |_{(5)}=0$. Thus, from the LaSalle theorem, $E_\mathrm{0w}$ is globally attractive. Thus, $E_\mathrm{0w}$ is globally stable if $R_{0}^{*}<1$. $\square$

: Proof of Theorem 2

Proof

If $R_{0}^{*}>1$, then system (5) has a unique endemic equilibrium $E_\mathrm{w}^{*}$. Let

$$\begin{aligned} \begin{aligned}&V_{i}=S_\mathrm{hw}^{*} \left( \frac{S_\mathrm{h}}{S_\mathrm{hw}^{*}}- \ln \left( \frac{S_\mathrm{h}}{S_\mathrm{hw}^{*}}\right) -1 \right) ,i=1,2,\\&V_{3}=I_\mathrm{hw}^{*} \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}- \ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) -1 \right) , \\&V_{4}=I_\mathrm{vw}^{*} \left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}- \ln \left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}\right) -1 \right) . \end{aligned} \end{aligned}$$

(38)

Differentiate $V_{i}$ along the solution of system (5). One has

$$\begin{aligned}&\frac{\hbox {d}V_{i}}{\hbox {d}t}\bigg |_{(5)}\\&\quad =\left( 1-\frac{S_\mathrm{hw}^{*}}{S_\mathrm{h}}\right) \left( \varLambda _\mathrm{h} -a\beta _{1}\frac{I_\mathrm{v}S_\mathrm{h}}{N_\mathrm{h}}-\beta _{3}\frac{I_\mathrm{h}S_\mathrm{h}}{N_\mathrm{h}}-d_\mathrm{h}S_\mathrm{h} \right) \\&\quad =\,\left( 1-\frac{S_\mathrm{hw}^{*}}{S_\mathrm{h}}\right) \bigg ( \frac{a\beta _{1}}{N_\mathrm{h}}(I_\mathrm{vw}^*S_\mathrm{hw}^*-I_\mathrm{v}S_\mathrm{h})+ \frac{ \beta _{3}}{N_\mathrm{h}}(I_\mathrm{hw}^*S_\mathrm{hw}^*-I_\mathrm{h}S_\mathrm{h})\\&\qquad +\,d_\mathrm{h}(S_\mathrm{hw}^*-S_\mathrm{h})\bigg )\\&\quad = -\,\frac{d_\mathrm{h}}{S_\mathrm{h}}\left( S_\mathrm{h}-S_\mathrm{hw}^{*}\right) ^{2} +\frac{a\beta _{1}I_\mathrm{vw}^*S_\mathrm{hw}^*}{N_\mathrm{h}}\left( 1-\frac{S_\mathrm{hw}^{*}}{S_\mathrm{h}} -\frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}} +\frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}} \right) \\&\qquad +\, \frac{ \beta _{3}I_\mathrm{hw}^*S_\mathrm{hw}^*}{N_\mathrm{h}} \left( 1-\frac{S_\mathrm{hw}^{*}}{S_\mathrm{h}} -\frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}} +\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} \right) \\&\quad \le \frac{a\beta _{1}I_\mathrm{vw}^*S_\mathrm{hw}^*}{N_\mathrm{h}}\left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}-\ln \left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}\right) -\frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}+\ln \left( \frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}\right) \right) \\&\qquad +\, \frac{ \beta _{3}I_\mathrm{hw}^*S_\mathrm{hw}^*}{N_\mathrm{h}} \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} -\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}+\ln \left( \frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}\right) \right) ,\\&\quad \triangleq l_{21}G_{21}+l_{43}G_{43}, i=1,2, \\&\frac{\hbox {d}V_{3}}{\hbox {d}t}\bigg |_{(5)}\\&\quad =\left( 1-\frac{I_\mathrm{hw}^{*}}{I_\mathrm{h}}\right) \left( a\beta _{1}\frac{I_\mathrm{v}S_\mathrm{h}}{N_\mathrm{h}}+\beta _{3}\frac{I_\mathrm{h}S_\mathrm{h}}{N_\mathrm{h}}-rI_\mathrm{h}- d_\mathrm{h} I_\mathrm{h}\right) \\&\quad =\left( 1-\frac{I_\mathrm{hw}^{*}}{I_\mathrm{h}}\right) \left( \frac{a\beta _{1}}{N_\mathrm{h}}\left( I_vS_\mathrm{h}-\frac{I_\mathrm{vw}^*S_\mathrm{hw}^*I_\mathrm{h}}{I_\mathrm{hw}^*} \right) + \frac{ \beta _{3}}{N_\mathrm{h}}\left( I_hS_\mathrm{h}- I_hS_\mathrm{hw}^*\right) \right) \\&\quad \le \frac{a\beta _{1}I_\mathrm{vw}^*S_\mathrm{hw}^*}{N_\mathrm{h}}\left( \frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}-\ln \left( \frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} +\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) \right) \\&\qquad +\, \frac{ \beta _{3}I_\mathrm{hw}^*S_\mathrm{hw}^*}{N_\mathrm{h}} \left( \frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}-\ln \left( \frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} +\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) \right) \\&\quad \triangleq l_{32}G_{32}+l_{34}G_{34}, \\&\frac{\hbox {d}V_{4}}{\hbox {d}t}\bigg |_{(5)} =\left( 1-\frac{I_\mathrm{vw}^{*}}{I_\mathrm{v}}\right) \left( a\beta _{2}\frac{I_\mathrm{h}(N_\mathrm{v}-I_\mathrm{v})}{N_\mathrm{h}}-d_\mathrm{v}I_\mathrm{v} \right) \\&\quad \le \frac{a\beta _{2}N_\mathrm{v}}{N_\mathrm{h}}I_\mathrm{hw}^{*} \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} -\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}+\ln \left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}\right) \right) \\&\quad \triangleq l_{13}G_{13}. \end{aligned}$$

Here, $l_{21}=l_{32}=\frac{a\beta _{1}I_\mathrm{vw}^*S_\mathrm{hw}^*}{N_\mathrm{h}}$, $l_{34}=l_{43}=\frac{ \beta _{3}I_\mathrm{hw}^*S_\mathrm{hw}^*}{N_\mathrm{h}}$, $l_{13}=\frac{a\beta _{2}N_\mathrm{v}}{N_\mathrm{h}}I_\mathrm{hw}^{*}$, $G_{21}=\frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}-\ln \left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}\right) -\frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}+\ln \left( \frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}\right) ,$$G_{43}=\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} -\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}+\ln \left( \frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}\right) ,$$G_{32}=\frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}-\ln \left( \frac{I_\mathrm{v}S_\mathrm{h}}{I_\mathrm{vw}^{*}S_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} +\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right)$, $G_{34}= \frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}-\ln \left( \frac{I_\mathrm{h}S_\mathrm{h}}{I_\mathrm{hw}^{*}S_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} +\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right)$, $G_{13}=\frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}} -\ln \left( \frac{I_\mathrm{h}}{I_\mathrm{hw}^{*}}\right) -\frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}+\ln \left( \frac{I_\mathrm{v}}{I_\mathrm{vw}^{*}}\right) .$

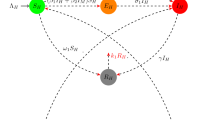
Now, denote a weight matrix $M=(a_{ij})_{4\times 4}$ and the corresponding weighted digraph $({\mathcal {G}}, M)$ is shown in Fig. 14. Denote $s({\mathcal {C}})$ be the arc set of ${\mathcal {C}}$. Then, for each cycle ${\mathcal {C}}$, one has $\sum \nolimits _{(i,j)\in s({\mathcal {C}})}G_{ij}=0$. Thus, from Theorem 3.5 in Shuai and Van den Driessche (2013), there exist ${\bar{c}}_{i}\ge 0,~i=1,2,\ldots ,4,$ such that $V=\mathop \sum \nolimits _{i=1}^{4}{\bar{c}}_{i}V_{i}$ is a Lyapunov function of system (5) and $\frac{\hbox {d}V}{\hbox {d}t}\big |_{(5)}\le 0$. Using the same step in Wang and Zhao (2019), $V=\mathop \sum \nolimits _{i=1}^{4}{\bar{c}}_{i}V_{i}$ is a positive definite function. So, $E_\mathrm{w}^*$ is stable. $E_\mathrm{w}^*$ is the largest positively invariant set contained in $\frac{\hbox {d}V }{\hbox {d}t}\big |_{(5)}=0$. Thus, from the LaSalle theorem, $E_\mathrm{w}^*$ is globally attractive. Thus, $E_\mathrm{w}^*$ is globally stable in the region $\varGamma \backslash E_\mathrm{0w}$. $\square$

Fig. 14

The weighted digraph $({\mathcal {G}}, M)$

: Discontinuous Bifurcation

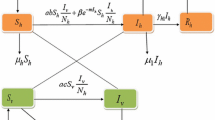
Denote $E_\mathrm{f}^{*}=(S_\mathrm{hf}^{*},I_\mathrm{hf}^{*},I_\mathrm{vf}^{*})$ be any endemic equilibrium of system (4). Assume that (H1), the conditions of (F1), ${\bar{\alpha }}_{1}(I_\mathrm{hf2})>0$, ${\bar{\alpha }}_{2}(I_\mathrm{hf2})>0$ and $\varDelta (I_\mathrm{hf2})<0$ hold. When $I_\mathrm{hf}^{*}<b$, $E_\mathrm{f}^{*}= E_\mathrm{hf0}$ is stable, and when $I_\mathrm{hf}^{*}>b$, $E_\mathrm{f}^{*}= E_\mathrm{hf2}$ is unstable. Furthermore, if $I_\mathrm{hf}^{*}=b$, then there exist a pair of conjugate complex eigenvalues for $J(E_\mathrm{f}^{*})$. Hence, we expect a limit cycle can bifurcate when $I_\mathrm{hf}^{*}$ passes through b, which is called discontinuous bifurcation (Leine and Nijmeijer 2004; Clarke et al. 2008; Leine and Van Campen 2006) since system (4) is non-smooth at $I_\mathrm{hf}^{*}=b$. Note that equilibrium $E_{b}^{*}=\left( \frac{d_\mathrm{h}N_\mathrm{h}-(\mu _{1}+r+d_\mathrm{h})b}{d_\mathrm{h}},b,\frac{a\beta _{2}N_\mathrm{v}b}{a\beta _{2}b+d_\mathrm{v}N_\mathrm{h}}\right)$ for $I_\mathrm{hf}^{*}=b$.

Let $J_{-}(E_{b}^{*})$ and $J_{+}(E_{b}^{*})$ denote the left and right Jacobian of system (4) at endemic equilibrium $E_{b}^{*}$, respectively. Then,

$$\begin{aligned}&J_{\pm }(E_{b}^{*})\\&\quad =\left[ \begin{array}{ccc} -\beta _{3}\frac{I_\mathrm{hf}^{*}}{N_\mathrm{h}}-a\beta _{1}\frac{I_\mathrm{vf}^{*}}{N_\mathrm{h}}-d_\mathrm{h} &{} -\beta _{3}\frac{S_\mathrm{hf}^{*}}{N_\mathrm{h}} &{} -a\beta _{1}\frac{S_\mathrm{hf}^{*}}{N_\mathrm{h}} \\ \beta _{3}\frac{I_\mathrm{hf}^{*}}{N_\mathrm{h}}+ a\beta _{1}\frac{I_\mathrm{vf}^{*}}{N_\mathrm{h}} &{} \beta _{3}\frac{S_\mathrm{hf}^{*}}{N_\mathrm{h}}-(\mu _{1}+r+d_\mathrm{h})-\mu '_{\pm }(b)b &{} a\beta _{1}\frac{S_\mathrm{hf}^{*}}{N_\mathrm{h}} \\ 0 &{} a\beta _{2}\frac{(N_\mathrm{v}-I_\mathrm{vf}^{*})}{N_\mathrm{h}} &{} -a\beta _{2}\frac{I_\mathrm{hf}^{*}}{N_\mathrm{h}}-d_\mathrm{v}\\ \end{array} \right] , \end{aligned}$$

where $(S_\mathrm{hf}^{*},~I_\mathrm{hf}^{*},~I_\mathrm{vf}^{*})=E_{b}^{*}$, $\mu '_{+}(b)=-\frac{\mu _{1}-\mu _{0}}{2(b-{\underline{b}})}$ and $\mu '_{-}(b)=0.$ It is obvious that $J_{-}(E_{b}^{*})\ne J_{+}(E_{b}^{*})$ when $I_\mathrm{hf}^{*}=b.$ Note $J_{-}\triangleq J_{-}(E_{b}^{*})$ and $J_{+}\triangleq J_{+}(E_{b}^{*})$. We have real parts of eigenvalues of $J_{-}$ are all negative, and there exists at least one positive real part eigenvalue of $J_{+}$. Then, there exists a jump from $J_{-}$ to $J_{+}$.

It is difficult to study the stability of equilibrium $E_{b}^{*}$. Here, we introduce the smooth approximation system and the generalized Jacobian matrix of Clarke (Leine and Nijmeijer 2004; Clarke et al. 2008; Leine and Van Campen 2006). In our study, the smooth approximation system of (4) is as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \frac{\hbox {d}S_\mathrm{h}}{\hbox {d}t}=d_\mathrm{h}N_\mathrm{h}-a\beta _{1}\frac{I_\mathrm{v}S_\mathrm{h}}{N_\mathrm{h}}-\beta _{3}\frac{I_\mathrm{h}S_\mathrm{h}}{N_\mathrm{h}}-d_\mathrm{h}S_\mathrm{h},\\ \frac{\hbox {d}I_\mathrm{h}}{\hbox {d}t}=a\beta _{1}\frac{I_\mathrm{v}S_\mathrm{h}}{N_\mathrm{h}}+\beta _{3}\frac{I_\mathrm{h}S_\mathrm{h}}{N_\mathrm{h}} - \left( \mu _{0}+(\mu _{1}-\mu _{0})\frac{2(b-{\underline{b}})}{ \epsilon I_\mathrm{h}+(2-\epsilon )b-2{\underline{b}}}\right) I_\mathrm{h} -rI_\mathrm{h}-d_\mathrm{h} I_\mathrm{h},\\ \frac{\hbox {d}I_\mathrm{v}}{\hbox {d}t}=a\beta _{2}\frac{I_\mathrm{h}(N_\mathrm{v}-I_\mathrm{v})}{N_\mathrm{h}}-d_\mathrm{v}I_\mathrm{v}, \end{array}\right. \nonumber \\ \end{aligned}$$

(39)

with $0\le \epsilon \le 1$, and the generalized Jacobian matrix of Clarke at $E_{b}^{*}$ is

$$\begin{aligned} J={\bar{co}}\{J_{-},~J_{+}\}=\{\epsilon J_{-}+(1-\epsilon )J_{+}~|~\epsilon \in [0,~1]\}. \end{aligned}$$

Obviously, $E_{b}^{*}$ is endemic equilibrium of system (39). Let $J(\epsilon )=\epsilon J_{-}+(1-\epsilon )J_{+}$. Then, $J(\epsilon )$ is Jacobian matrix at $E_{b}^{*}$ of system (39). The characteristic equation of $J(\epsilon )$ is as follows:

$$\begin{aligned} \lambda ^{3}+ \breve{\alpha }_{1}\lambda ^{2}+ \breve{\alpha }_{2}\lambda + \breve{\alpha }_{3} =0, \end{aligned}$$

(40)

where

$$\begin{aligned} \breve{\alpha }_{1}= & {} {\bar{\alpha }}_{1}(b)+\frac{ (\mu _{1}-\mu _{0})(1-\epsilon )}{2},\\ \breve{\alpha }_{2}= & {} {\bar{\alpha }}_{2}(b)+ \left( \beta _{3}\frac{b}{N_\mathrm{h}}+\frac{a\beta _{1}}{N_\mathrm{h}}\frac{a\beta _{2}N_\mathrm{v}b}{a\beta _{2}b+d_\mathrm{v}N_\mathrm{h}}+d_\mathrm{h}+a\beta _{2}\frac{b}{N_\mathrm{h}}+d_\mathrm{v}\right) \frac{ (\mu _{1}-\mu _{0})(1-\epsilon )}{2},\\ \breve{\alpha }_{3}= & {} {\bar{\alpha }}_{3}(b)+ \left( \beta _{3}\frac{b}{N_\mathrm{h}}+\frac{a\beta _{1}}{N_\mathrm{h}}\frac{a\beta _{2}N_\mathrm{v}b}{a\beta _{2}b+d_\mathrm{v}N_\mathrm{h}}+d_\mathrm{h}\right) \left( a\beta _{2}\frac{b}{N_\mathrm{h}}+d_\mathrm{v}\right) \frac{ (\mu _{1}-\mu _{0})(1-\epsilon )}{2}, \end{aligned}$$

in which ${\bar{\alpha }}_{i}(b)={\bar{\alpha }}_{i}|_{I_\mathrm{h}=b}, i=1,2,3.$

When $\epsilon =0$, the real parts of all roots of Eq. (40) are negative. When $\epsilon =1$, there exist a negative real root and the real parts of two roots of Eq. (40) which are positive. We know that $\breve{\alpha }_{3}>0$ always holds which implies 0 is not a root of Eq. (40). Hence, there is a $0<\epsilon ^{*}<1$ such that Eq. (40) has a pair of purely imaginary roots $\pm i\omega ^{*}~(\omega >0)$ when $\epsilon =\epsilon ^{*}$. Therefore, the discontinuous Hopf bifurcation (Leine and Nijmeijer 2004) may occur. Now, we tend to find such $\epsilon ^{*}$. Substituting $i\omega ~ (\omega >0)$ into (40) and separating the real and imaginary parts give

$$\begin{aligned} \left\{ \begin{array}{lll} \breve{\alpha }_{2}-\omega ^{2}=0,\\ \breve{\alpha }_{3}-\breve{\alpha }_{1}\omega ^{2}=0.\\ \end{array}\right. \end{aligned}$$

(41)

Then, $\breve{\alpha }_{1}\breve{\alpha }_{2}-\breve{\alpha }_{3}=0.$ So, we can get the unique $\epsilon =\epsilon ^{*}$ and $\omega =\omega ^{*},$ where

$$\begin{aligned} \begin{array}{lll} \epsilon ^{*}=1-\frac{-A_{1}+\sqrt{A_{1}^{2}-4A_{1}A_{2}}}{2A_{0}}<1,~~\omega ^{*}=\sqrt{\breve{\alpha }_{2}}, \end{array} \end{aligned}$$

(42)

in which

$$\begin{aligned} \begin{aligned} A_{0}=&\left( \beta _{3}\frac{b}{N_\mathrm{h}}+\frac{a\beta _{1}}{N_\mathrm{h}}\frac{a\beta _{2}N_\mathrm{v}b}{a\beta _{2}b+d_\mathrm{v}N_\mathrm{h}}+d_\mathrm{h}+a\beta _{2}\frac{b}{N_\mathrm{h}}+d_\mathrm{v}\right) \frac{ (\mu _{1}-\mu _{0})^{2}}{4},\\ A_{1}=&\left( \beta _{3}\frac{b}{N_\mathrm{h}}+\frac{a\beta _{1}}{N_\mathrm{h}}\frac{a\beta _{2}N_\mathrm{v}b}{a\beta _{2}b+d_\mathrm{v}N_\mathrm{h}}+d_\mathrm{h}+a\beta _{2}\frac{b}{N_\mathrm{h}}+d_\mathrm{v}\right) {\bar{\alpha }}_{1}(b)+{\bar{\alpha }}_{2}(b)\\&-\left( \beta _{3}\frac{b}{N_\mathrm{h}}+\frac{a\beta _{1}}{N_\mathrm{h}}\frac{a\beta _{2}N_\mathrm{v}b}{a\beta _{2}b+d_\mathrm{v}N_\mathrm{h}}+d_\mathrm{h}\right) \left( a\beta _{2}\frac{b}{N_\mathrm{h}}+d_\mathrm{v}\right) ,\\ A_{2}=&{\bar{\alpha }}_{1}(b){\bar{\alpha }}_{2}(b)-{\bar{\alpha }}_{3}(b)<0. \end{aligned} \end{aligned}$$

Then, $(\epsilon ^{*},~\omega ^{*})$ is a solution of Eq. (40). It implies that $\pm i\omega ^{*}$ is a pair of purely imaginary roots of Eq. (40) when $\epsilon =\epsilon ^{*}$ (Fig. 15). we can obtain the following result.

Theorem 15

Assume that (H1), the conditions of (F1), ${\bar{\alpha }}_{1}(I_\mathrm{hf2})>0$, ${\bar{\alpha }}_{2}(I_\mathrm{hf2})>0$, $\varDelta (I_\mathrm{hf2})<0$ and $\frac{-A_{1}+\sqrt{A_{1}^{2}-4A_{1}A_{2}}}{2A_{0}}<1$ hold. Denote $E_\mathrm{f}^{*}=(S_\mathrm{hf}^{*},~I_\mathrm{hf}^{*},~I_\mathrm{vf}^{*})$ be any endemic equilibrium of system (4). When $I_\mathrm{hf}^{*}=b$, we have the following:

• (C1) The endemic equilibrium $E_\mathrm{f}^{*}$ of the smooth approximation system (39) of system (4) is stable for all $0\le \epsilon <\epsilon ^{*}$ and unstable for all $\epsilon ^{*}<\epsilon \le 1$.

• (C2) A discontinuous bifurcation occurs at endemic equilibrium $E_\mathrm{f}^{*}$ of the smooth approximation system (39) of system (4) as $\epsilon$ increasingly passes through $\epsilon ^{*}$. That is, system (39) has a branch of periodic solutions bifurcating from the endemic equilibrium $E_\mathrm{f}^{*}$.

Fig. 15

Sets of eigenvalues of the generalized Jacobian J. It has three paths from $\epsilon =0$ to $\epsilon =1$ with $\epsilon ^{*}=0.4892$ and $\omega ^{*}=0.01237$. Here, $d_\mathrm{v}=0.175,$$\beta _{1}= 0.10895$, $\beta _{3}= 0.03$, $r=0.07$, $\mu _{0}= 0.08035$, $\mu _{1}=0.081,$ and all other parameters values are shown in Table 2 (Color Figure Online)

: Proof of Theorem 13

Proof

The translation $x=S_\mathrm{h}-S_\mathrm{h}^{*}$, $y=I_\mathrm{h}-I_\mathrm{h}^{*}$, $x=I_\mathrm{v}-I_\mathrm{v}^{*}$ brings $E^{*}$ to the origin. Expanding the right-hand sides of the resulting system in a Taylor series about the origin, we obtain

$$\begin{aligned} \left\{ \begin{aligned} \frac{\hbox {d}x}{\hbox {d}t}=&-m_{2}x-m_{3}y-\frac{a\beta _{1}S_\mathrm{h}^{*}}{N_\mathrm{h}}z-\frac{\beta _{3}}{N_\mathrm{h}}xy-\frac{a\beta _{1}}{N_\mathrm{h}}xz,\\ \frac{\hbox {d}y}{\hbox {d}t}=&(m_{2}-d_\mathrm{h})x+(m_{3}-m_{1})y+ \frac{a\beta _{1}S_\mathrm{h}^{*}}{N_\mathrm{h}}z+\frac{\beta _{3}}{N_\mathrm{h}}xy+ \frac{2(\mu _{1}-\mu _{0})(b-{\underline{b}})(b-2{\underline{b}})}{( I_\mathrm{h}^*+b-2{\underline{b}})^{3}}y^{2} \\&+\frac{a\beta _{1}}{N_\mathrm{h}}xz+ {\mathcal {O}}(|x,y,z|^{3}),\\ \frac{\hbox {d}z}{\hbox {d}t}=&\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{I_\mathrm{h}^{*}}y-m_{4}z-\frac{a\beta _{2}}{N_\mathrm{h}}yz. \end{aligned}\right. \nonumber \\ \end{aligned}$$

(43)

The generalized eigenvectors corresponding to $\lambda =0$ of Jacobian matrix $J_{E^{*}}$ are

$$\begin{aligned} V_{1}=\left( -\frac{m_{1}m_{4}}{d_\mathrm{h}},~m_{4},~\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{I_\mathrm{h}^{*}}\right) ',~ V_{2}=\left( -\frac{1}{d_\mathrm{h}^{2}}(d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}),~1,~0 \right) ', \end{aligned}$$

which satisfy $J_{E^{*}}V_{1}=0$ and $J_{E^{*}}V_{2}=V_{1}$. $V_{3}=\Big ( -m_{3}-\frac{m_{2}^{2}}{m_{2}-d_\mathrm{h}},m_{1}+m_{2}-m_{3},-\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{I_\mathrm{h}^{*}}\Big )'$ is the eigenvector of $\lambda =-{\bar{\alpha }}_{1}$. Let

$$\begin{aligned} T=(T_{ij})_{3\times 3}=(V_{1},~V_{2},~V_{3}), \end{aligned}$$

(44)

then under the non-singular linear transformation

$$\begin{aligned} ( x,~y,~z)^\mathrm{T}=T ( x,~y,~z)^\mathrm{T}, \end{aligned}$$

(45)

then, system (43) becomes

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\hbox {d}u_{1}}{\hbox {d}t}=u_{2}+L_{20}u_{1}^{2}+L_{11}u_{1}u_{2}+L_{02}u_{2}^{2}+u_{3}\cdot {\mathcal {O}}(|u_{1},u_{2}|)+ {\mathcal {O}}(|u_{1},u_{2},u_{3}|^{3}),\\&\frac{\hbox {d}u_{2}}{\hbox {d}t}=M_{20}u_{1}^{2}+M_{11}u_{1}u_{2}+M_{02}u_{2}^{2}+u_{3}\cdot {\mathcal {O}}(|u_{1},u_{2}|)+ {\mathcal {O}}(|u_{1},u_{2},u_{3}|^{3}),\\&\frac{\hbox {d}u_{3}}{\hbox {d}t}=-{\bar{\alpha }}_{1}u_{3}+K_{20}u_{1}^{2}+K_{11}u_{1}u_{2}+K_{02}u_{2}^{2}+u_{3}\cdot {\mathcal {O}}(|u_{1},u_{2}|)+ {\mathcal {O}}(|u_{1},u_{2},u_{3}|^{3}),\\ \end{aligned}\right. \end{aligned}$$

(46)

in which $L_{20}=\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}}l_{20},$   $M_{20}=\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}}m_{20},$  $M_{11}=\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}}m_{11},$  

$$\begin{aligned} L_{11}= & {} \frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}d_\mathrm{h}^{4}} \left( d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}-d_\mathrm{h}^{2}\right) \\&\times \left( \frac{\beta _{3}m_{1}m_{4}}{N_\mathrm{h}}+\,(2d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4})\,\left( \frac{\beta _{3}m_{4}}{N_\mathrm{h}}+\frac{a\beta _{1}d_\mathrm{v}I_\mathrm{v}^{*}}{N_\mathrm{h}I_\mathrm{h}^{*}}\right) \right) +\frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}} \\&\times \left[ \left( \frac{1}{d_\mathrm{h}^{2}}\left( d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}\right) \left( m_{1}+m_{2}-m_{3}-\left( m_{3}+\frac{m_{2}^{2}}{m_{2}-d_\mathrm{h}}\right) \right) \frac{a\beta _{2}}{N_\mathrm{h}}\right. \right. \\&\left. -\frac{m_{4}}{d_\mathrm{h}^{2}}(d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}) \frac{4(\mu _{1}-\mu _{0})(b-{\underline{b}})(b-2{\underline{b}})}{( I_\mathrm{h}^*+b-2{\underline{b}})^{3}}\right] , \\ L_{02}= & {} \frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}d_\mathrm{h}^{2}} \left( d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}) \left( \frac{1}{d_\mathrm{h}^{2}}(d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}-d_\mathrm{h}^{2}\right) \frac{\beta _{3}}{N_\mathrm{h}}\right. \\&\left. -\, \frac{2(\mu _{1}-\mu _{0})(b-{\underline{b}})(b-2{\underline{b}})}{(I_\mathrm{h}^*+b-2{\underline{b}})^{3}} \right) ,\\ M_{02}= & {} \frac{d_\mathrm{v}I_\mathrm{v}^{*}}{|T|I_\mathrm{h}^{*}} \left[ \frac{1}{d_\mathrm{h}^{2}}(d_\mathrm{h}m_{1}+d_\mathrm{h}m_{4}-m_{1}m_{4}) \left( -\frac{m_{1}m_{4}}{d_\mathrm{h}} - \frac{m_{2}^{2}}{m_{2}-d_\mathrm{h}}+{\bar{\alpha }}_{1}-m_{3}\right) \frac{\beta _{3}}{N_\mathrm{h}}\right. \\&\left. +\left( \frac{m_{1}m_{4}}{d_\mathrm{h}}+\,\frac{m_{2}^{2}}{m_{2}-d_\mathrm{h}}+m_{3} \right) \frac{2(\mu _{1}-\mu _{0})(b-{\underline{b}})(b-2{\underline{b}})}{(I_\mathrm{h}^*+b-2{\underline{b}})^{3}} \right] ,\\ K_{20}= & {} L_{20}+\frac{a\beta _{2}m_{4}}{N_\mathrm{h}},\\ K_{11}= & {} L_{11}+\frac{a\beta _{2}}{N_\mathrm{h}},\\ K_{02}= & {} L_{02}. \end{aligned}$$

We reduce system (46) to a two-dimensional center manifold which corresponds to a pair of simple zero eigenvalues. According to Kuznetsov (1995), there exists a center manifold for system (46) which can be locally be represented as follows

$$\begin{aligned}&W^{c}=\{(u_{1},~u_{2},~u_{3})~|~u_{3}=F(u_{1},~u_{2}),~|u_{1}|<\varepsilon _{1},~ |u_{2}|\\&\quad <\varepsilon _{2}, ~F(0,~0)=0,~ DF(0,~0)=0\} \end{aligned}$$

for $\varepsilon _{1}$ and $\varepsilon _{2}$ sufficiently small. So, we consider the center manifold

$$\begin{aligned} u_{3}=F(u_{1},~u_{2})=s_{0}u_{1}^{2}+s_{1}u_{1}u_{2}+s_{2}u_{2}^{2}+{\mathcal {O}}(|u_{1},u_{2}|^{3}). \end{aligned}$$

(47)

By putting the center manifold (47) into the third equation of (46), and then by equating powers of $u_{1}^{2}$, $u_{1}u_{2}$ and $u_{2}^{2}$ on both sides, we can calculate the coefficients of the center manifold as follows:

$$\begin{aligned} s_{0}=\frac{K_{20}}{{\bar{\alpha }}_{1}},~ s_{1}=\frac{1}{{\bar{\alpha }}_{1}^{2}}({\bar{\alpha }}_{1}K_{11}-2K_{20}),~s_{2}=\frac{1}{{\bar{\alpha }}_{1}^{3}}({\bar{\alpha }}_{1}^{2}K_{02}-{\bar{\alpha }}_{1}K_{11}+2K_{20}). \end{aligned}$$

System (46) restricted to the center manifold is given by

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\hbox {d}u_{1}}{\hbox {d}t}=u_{2}+L_{20}u_{1}^{2}+L_{11}u_{1}u_{2}+L_{02}u_{2}^{2}+ {\mathcal {O}}(|u_{1},u_{2}|^{3}),\\&\frac{\hbox {d}u_{2}}{\hbox {d}t}=M_{20}u_{1}^{2}+M_{11}u_{1}u_{2}+M_{02}u_{2}^{2}+ {\mathcal {O}}(|u_{1},u_{2}|^{3}). \end{aligned}\right. \end{aligned}$$

(48)

Using the following transformation

$$\begin{aligned}&u_{1}=\eta _{1}+\frac{1}{2}(L_{11}+M_{02})\eta _{1}^{2}+L_{02}\eta _{1}\eta _{2}+{\mathcal {O}}(|\eta _{1},\eta _{2}|^{3}),~\\&u_{2}=\eta _{2}-L_{20}\eta _{1}^{2}+M_{02}\eta _{1}\eta _{2}+{\mathcal {O}}(|\eta _{1},\eta _{2}|^{3}), \end{aligned}$$

then system (48) is topologically equivalent to the normal form (30). $\square$