Complex Far-Field Geometries Determine the Stability of Solid Tumor Growth with Chemotaxis

Abstract

In this paper, we develop a sharp interface tumor growth model to study the effect of the tumor microenvironment using a complex far-field geometry that mimics a heterogeneous distribution of vasculature. Together with different nutrient uptake rates inside and outside the tumor, this introduces variability in spatial diffusion gradients. Linear stability analysis suggests that the uptake rate in the tumor microenvironment, together with chemotaxis, may induce unstable growth, especially when the nutrient gradients are large. We investigate the fully nonlinear dynamics using a spectrally accurate boundary integral method. Our nonlinear simulations reveal that vascular heterogeneity plays an important role in the development of morphological instabilities that range from fingering and chain-like morphologies to compact, plate-like shapes in two dimensions.

Appendices

Appendix A: Linear Stability Analysis

The governing equations are

$$\begin{aligned} \varDelta \sigma -\mu _{\mathrm {i}}^{2} \sigma&=0 \text{ in } \varOmega _{\mathrm {i}}, \end{aligned}$$

(48)

$$\begin{aligned} \ [\sigma ]_{\varGamma }&=0, \end{aligned}$$

(49)

$$\begin{aligned} \left[ D \frac{\partial \sigma }{\partial n}\right] _{\varGamma }&=0, \end{aligned}$$

(50)

$$\begin{aligned} \sigma |_{\varGamma _{\infty }}&=1. \end{aligned}$$

(51)

and

$$\begin{aligned} \varDelta p&=0 \text{ in } \varOmega _{1}, \end{aligned}$$

(52)

$$\begin{aligned} {p}&=\mathscr {G}^{-1} \kappa +\left( \mathscr {P}-\chi _{\sigma }\right) \sigma -\mathscr {A} \frac{\mathbf {x} \cdot \mathbf {x}}{2 {d}}\text { on } \varGamma . \end{aligned}$$

(53)

$$\begin{aligned} V&=-\frac{\partial p}{\partial n}+\mathscr {P}\frac{\partial \sigma }{\partial n}-\mathscr {A} \frac{\mathbf {n} \cdot \mathbf {x}}{d}\text { on } \varGamma . \end{aligned}$$

(54)

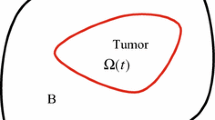
Consider a perturbed tumor interface $\varGamma$:

$$\begin{aligned} r(t)=R(t)+\delta (t) e^{i l \theta }. \end{aligned}$$

(55)

In cylindrical coordinates, the modified Helmholtz equation is

$$\begin{aligned} r^{-1}\left( r \sigma _{r}\right) _{r}+r^{-2} \sigma _{\theta \theta }+r^{-2} \sigma _{z z}-\mu _{i}^{2} \sigma =0 \text{ in } \varOmega _{i}. \end{aligned}$$

(56)

Assuming axial symmetry, e.g., $\sigma =\sigma (r, \theta )$ is independent of z, then

$$\begin{aligned} r^{-1}\left( r \sigma _{r}\right) _{r}+r^{-2} \sigma _{\theta \theta }-\mu _{i}^{2} \sigma =0. \end{aligned}$$

(57)

1.1 Radial Solutions

We first consider the radial solution, i.e., $\sigma =\sigma (r)$, then (57) reduces to the modified Bessel differential equation

$$\begin{aligned} \left( r^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+r \frac{\mathrm{d}}{\mathrm{d} r}-\mu _{i}^{2} r^{2}\right) \sigma (r)=0 \text{ in } \varOmega _{i}. \end{aligned}$$

(58)

Recall the general form of modified Bessel differential equation is

$$\begin{aligned} \left( x^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}+x \frac{\mathrm{d}}{\mathrm{d}x}-\left( \beta ^{2} x^{2}+n^{2}\right) \right) y(x)=0. \end{aligned}$$

(59)

The general solutions are

$$\begin{aligned} y= & {} a_{1} J_{n}(-i \beta x)+a_{2} Y_{n}(-i \beta x) \nonumber \\= & {} c_{1} I_{n}(\beta x)+c_{2} K_{n}(\beta x), \end{aligned}$$

(60)

where $J_{n}(x)$ is the Bessel function of the first kind, $Y_{n}(x)$ is the Bessel function of the second kind, $I_{n}(x)$ is a modified Bessel function of the first kind and $K_{n}(x)$ is a modified Bessel function of the second kind.

The following recurrence relations are useful in the linear analysis

$$\begin{aligned} {} I_{n}^{\prime }(x)= & {} \frac{1}{2}\left( I_{n-1}(x)+I_{n+1}(x)\right) ,\nonumber \\ I_{n}^{\prime }(x)= & {} I_{n-1}(x)-\frac{n}{x} I_{n}(x)=\frac{n}{x} I_{n}(x)+I_{n+1}(x),\nonumber \\ I_{0}^{\prime }(x)= & {} I_{1}(x). \end{aligned}$$

(61)

$$\begin{aligned} K_{n}^{\prime }(x)= & {} -\frac{1}{2}\left( K_{n-1}(x)+K_{n+1}(x)\right) ,\nonumber \\ K_{n}^{\prime }(x)= & {} -K_{n-1}(x)-\frac{n}{x} K_{n}(x)=\frac{n}{x} K_{n}(x)-K_{n+1}(x),\nonumber \\ K_{0}^{\prime }(x)= & {} -K_{1}(x). \end{aligned}$$

(62)

The modified Bessel functions of the second kind all have the property that

$$\begin{aligned} K_{n}(x) \rightarrow \infty \text{ as } x \rightarrow 0. \end{aligned}$$

Hence, the constant $c_2$ in Eq. (60) must be zero. We therefore obtain

$$\begin{aligned} \sigma&=A_{1} I_{0}\left( \mu _{1} r\right)&{\text {in}}\ \varOmega _{1}, \end{aligned}$$

(63)

$$\begin{aligned} \sigma&=A_{2} I_{0}\left( \mu _{2} r\right) +A_{3} K_{0}\left( \mu _{2} r\right)&{\text {in}}\ \varOmega _{2}. \end{aligned}$$

(64)

Applying the boundary conditions (49), (50), (51) on the circles $r=R,R_\infty$, we have

$$\begin{aligned} A_{1} I_{0}\left( \mu _{1} R\right)&=A_{2} I_{0}\left( \mu _{2} R\right) +A_{3} K_{0}\left( \mu _{2} R\right) , \end{aligned}$$

(65)

$$\begin{aligned} 1&=A_{2} I_{0}\left( \mu _{2} R_{\infty }\right) +A_{3} K_{0}\left( \mu _{2} R_{\infty }\right) , \end{aligned}$$

(66)

$$\begin{aligned} A_{1} \mu _{1} I_{1}\left( \mu _{1} R\right)&={D}\left( A_{2} \mu _{2} I_{1}\left( \mu _{2} R\right) -A_{3} \mu _{2} K_{1}\left( \mu _{2} R\right) \right) . \end{aligned}$$

(67)

Solving for $A_{1}, A_{2}, A_{3}$, we obtain

$$\begin{aligned} A_1= & {} \frac{D}{(D \mu _{2} R I_{0}(R \mu _{1}) \left( I_{1}(R \mu _{2})K_{0}(R_{\infty } \mu _{2})+K_{1}(R \mu _{2}) I_{0}(R_{\infty }\mu _{2}) \right) }\\&+\mu _{1} R I_{1} (R \mu _{1}) (K_{0}(R \mu _{2}) I_{0} (R_{\infty } \mu _{2}) -I_{0}(R \mu _{2}) K_{0} (R_{\infty } \mu _{2}))),\\ A_2= & {} \frac{D \mu _{2} I_{0}(R \mu _{1}) K_{1}(R \mu _{2}) +\mu _{1} I_{1}(R \mu _{1}) K_{0}(R \mu _{2})}{(D \mu _{2} I_{0} (R \mu _{1}) (I_{1} (R \mu _{2}) K_{0} (R_{\infty } \mu _{2}) +K_{1}(R \mu _{2}) I_{0} (R_{\infty } \mu _{2}) ) +\mu _{1} I_{1}(R \mu _{1}) (K_{0} (R \mu _{2}) I_{0} (R_{\infty } \mu _{2}) -I_{0}(R \mu _{2}) K_{0}(R_{\infty } \mu _{2}) ) )},\\ A_3= & {} \frac{\mu _{1} I_{0} (R \mu _{2}) I_{1} (R \mu _{1}) -D \mu _{2} I_{0}(R \mu _{1}) I_{1}(R \mu _{2})}{\mu _{1} I_{1}(R \mu _{1})((I_{0}(R \mu _{2}) K_{0}(R_{\infty } \mu _{2})-K_{0}(R \mu _{2}) I_{0}(R_{\infty } \mu _{2}))-D \mu _{2} I_{0}(R \mu _{1})(I_{1}(R \mu _{2}) K_{0}(R_{\infty } \mu _{2})+K_{1}(R \mu _{2}) I_{0}(R_{\infty }, \mu _{2}))}. \end{aligned}$$

1.2 Perturbation of Radial Solutions

Now we seek a solution of the modified Helmholtz equation on the perturbed circle given by (55). Since $\delta$ is the perturbation size, following Mullins and Sekerka (1963) we consider the Fourier expansion of the solution up to the first order in $\delta$:

$$\begin{aligned} \sigma (r, \theta )=\sigma _{i, 0}(r)+\delta e^{i l \theta } \sigma _{i, 1}(r) \text{ in } \varOmega _{i}. \end{aligned}$$

(68)

Note here that $r, \theta$ and $\delta$ are all functions of time t,  i.e., $r=r(t), \theta =\theta (t), \delta =\delta (t)$. Multiplying Eq. (57) by $r^2$, we obtain

$$\begin{aligned} \left( r^{2} \partial _{r}^{2}+r \partial _{r}+\partial _{\theta }^{2}-\mu _{i}^{2} r^{2}\right) \left( \sigma _{i, 0}(r)+\delta e^{i l \theta } \sigma _{i, 1}(r)\right)&=0&\text{ in } \varOmega _{i}, \end{aligned}$$

(69)

$$\begin{aligned} \left( r^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+r \frac{\mathrm{d}}{\mathrm{d}r}-\mu _{i}^{2} r^{2}\right) \sigma _{i, 0}(r)&=0&\text{ in } \varOmega _{i}, \end{aligned}$$

(70)

$$\begin{aligned} \left( r^{2} \frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+r \frac{\mathrm{d}}{\mathrm{d}r}-\left( \mu _{i}^{2} r^{2}+l^{2}\right) \right) \sigma _{i, 1}(r)&=0&\text{ in } \varOmega _{i}. \end{aligned}$$

(71)

Therefore, it is sufficient to consider the expression

$$\begin{aligned} \sigma&=A_{1} I_{0}\left( \mu _{1} r\right) +\delta e^{i l \theta } B_{1} I_{l}\left( \mu _{1} r\right)&\text{ in } \varOmega _{1}, \end{aligned}$$

(72)

$$\begin{aligned} \sigma&=A_{2} I_{0}\left( \mu _{2} r\right) +A_{3} K_{0}\left( \mu _{2} r\right) +\delta e^{i l \theta }\left( B_{2} I_{l}\left( \mu _{2} r\right) +B_{3} K_{l}\left( \mu _{2} r\right) \right)&\text{ in } \varOmega _{2}. \end{aligned}$$

(73)

Apply (49), (50), (51) on the interface $r=R+\delta e^{i l \theta }$ with $\delta \ll 1$. Orders higher than $O(\delta )$ are all discarded in the following calculations.

At O(1), the equations are the same as the radial solution.

The equations at $O(\delta )$ determine the coefficients $B_{1}, B_{2}, B_{3}:$

$$\begin{aligned}&B_{1} I_{l}\left( \mu _{1} R\right) =B_{2} I_{l}\left( \mu _{2} R\right) +B_{3} K_{l}\left( \mu _{2} R\right) +\left( A_{1} \mu _{1} I_{1}\left( \mu _{1} R\right) \right) \left( \frac{1}{D}-1\right) , \end{aligned}$$

(74)

$$\begin{aligned}&0=B_{2} I_{l}\left( \mu _{2} R_{\infty }\right) +B_{3} K_{l}\left( \mu _{2} R_{\infty }\right) , \end{aligned}$$

(75)

$$\begin{aligned}&\left( B_{1} \mu _{1}\left( I_{l-1}\left( \mu _{1} R\right) -\frac{l}{\mu _{1} R} I_{l}\left( \mu _{1} R\right) \right) +A_{1} \mu _{1}^{2}\left( I_{0}\left( \mu _{1} R\right) -\frac{1}{\mu _{1} R} I_{1}\left( \mu _{1} R\right) \right) \right) \nonumber \\&\quad =D\left( B_{2} \mu _{2}\left( I_{l-1}\left( \mu _{2} R\right) -\frac{l}{\mu _{2} R} I_{l}\left( \mu _{2} R\right) \right) \right. \nonumber \\&\qquad -B_{3} \mu _{2}\left( K_{l-1}\left( \mu _{2} R\right) +\frac{l}{\mu _{2} R} K_{l}\left( \mu _{2} R\right) \right) \nonumber \\&\qquad +\left. A_{2} \mu _{2}^{2}\left( I_{0}\left( \mu _{2} R\right) -\frac{1}{\mu _{2} R} I_{1}\left( \mu _{2} R\right) \right) +A_{3} \mu _{2}^{2}\left( K_{0}\left( \mu _{2} R\right) +\frac{1}{\mu _{2} R} K_{1}\left( \mu _{2} R\right) \right) \right) . \end{aligned}$$

(76)

Solving for $B_{1}, B_{2}, B_{3}$, we have

$$\begin{aligned} B_1= & {} \left( {D}(I_{l}(R_{\infty } \mu _{2}) K_{l}(R \mu _{2})-I_{l}(R \mu _{2}) K_{l}(R_{\infty } \mu _{2})) \mu _{2}(A_{2}(R I_{0}(R \mu _{2}) \mu _{2}-I_{1}(R \mu _{2}))\right. \\&+A_{3}(K_{1}(R \mu _{2})+R K_{0}(R \mu _{2}) \mu _{2}))\\&+A_{1} \mu _{1}\left( R I_{0}(R \mu _{1})(I_{l}(R \mu _{2}) K_{l}(R_{\infty } \mu _{2}) -I_{l}(R_{\infty } \mu _{2}) K_{l}(R \mu _{2})) \mu _{1}\right. \\&+I_{1}(R \mu _{1})\left( (l({D}-1)-1) I_{l}(R \mu _{2}) K_{l}(R_{\infty } \mu _{2})\right. \\&-R({D}-1) I_{l-1}(R \mu _{2}) \mu _{2} K_{l}(R_{\infty } \mu _{2}) +I_{l}(R_{\infty } \mu _{2})\\&\left. \left. \left. \left( K_{l}(R \mu _{2})-R({D}-1) \mu _{2}\left( K_{l-1}(R \mu _{2})+\frac{l K_{l}(R \mu _{2})}{R \mu _{2}}\right) \right) \right) \right) \right) \\&\quad /\left( R {D} I_{l-1}(R \mu _{2}) I_{l}(R \mu _{1}) K_{l}(R_{\infty } \mu _{2}) \mu _{2}+R(I_{l}(R_{\infty } \mu _{2}) K_{l}(R \mu _{2})\right. \\&-I_{l}(R \mu _{2}) K_{l}(R_{\infty } \mu _{2})) \mu _{1}\left( I_{l-1}\left( R \mu _{1}\right) -\frac{l I_{l}(R \mu _{1})}{R_{\mu _{1}}}\right) \\&+\left. {D} I_{l}\left( R \mu _{1}\right) \left( R I_{l}\left( R_{\infty } \mu _{2}\right) \mu _{2}\left( K_{l-1}\left( R \mu _{2}\right) +\frac{l K_{l}\left( R \mu _{2}\right) }{R \mu _{2}}\right) -l I_{l}\left( R \mu _{2}\right) K_{l}\left( R_{\infty } \mu _{2}\right) \right) \right) ,\\ B_2= & {} -\left( K_{l}(R_{\infty } \mu _{2})\left( I_{l}(R \mu _{1}) \mu _{2}(A_{2}(R I_{0}(R \mu _{2}) \mu _{2}-I_{1}(R \mu _{2}))+A_{3}(K_{1}(R \mu _{2})+R K_{0}\left( R \mu _{2}) \mu _{2})\right) {D}^{2}\right. \right. \\&+A_{1} \mu _{1}\left( I_{1}\left( R \mu _{1}\right) \left( {D} I_{l}\left( R \mu _{1}\right) +R({D}-1) \mu _{1}\left( I_{l-1}\left( R \mu _{1}\right) -\frac{l I_{l}\left( R \mu _{1}\right) }{R \mu _{1}}\right) \right) \right. \\&\left. \left. \left. -R {D} I_{0}\left( R \mu _{1}\right) I_{l}\left( R \mu _{1}\right) \mu _{1}\right) \right) \right) \\&/\left( {D}\left( R {D} I_{l-1}(R \mu _{2}) I_{l}(R \mu _{1}) K_{l}(R_{\infty } \mu _{2}) \mu _{2}+R(I_{l}(R_{\infty } \mu _{2}) K_{l}(R \mu _{2})\right. \right. \\&-I_{l}(R \mu _{2}) K_{l}(R_{\infty } \mu _{2})) \mu _{1} \left( I_{l-1}(R \mu _{1})-\frac{l I_{l}(R \mu _{1})}{R \mu _{1}}\right) \\&\left. \left. +{D} I_{l}(R \mu _{1})\left( R I_{l}(R_{\infty } \mu _{2}) \mu _{2} \left( K_{l-1}(R \mu _{2})+\frac{l K_{l}(R \mu _{2})}{R \mu _{2}}\right) -l I_{l}(R \mu _{2}) K_{l}(R_{\infty } \mu _{2})\right) \right) \right) ,\\ B_3= & {} \left( I_{l}\left( R_{\infty } \mu _{2}\right) \left( {D} I_{l}\left( R \mu _{1}\right) \left( {D} \mu _{2}\left( A_{2}\left( R I_{0}\left( R \mu _{2}\right) \mu _{2}-I_{1}\left( R \mu _{2}\right) \right) +A_{3}\left( K_{1}\left( R \mu _{2}\right) +R K_{0}\left( R \mu _{2}\right) \mu _{2}\right) \right) \right. \right. \right. \\&\left. -R I_{0}\left( R \mu _{1}\right) A_{1} \mu _{1}^{2}\right) +I_{1}\left( R \mu _{1}\right) A_{1} \mu _{1}\left( {D} I_{l}\left( R \mu _{1}\right) \right. \\&+R({D}-1) \mu _{1}\left( I_{l-1}\left( R \mu _{1}\right) \left. \left. \left. -\frac{l I_{l}\left( R \mu _{1}\right) }{R \mu _{1}}\right) \right) \right) \right) \\&\quad /\left( {D}\left( R {D} I_{l-1}\left( R \mu _{2}\right) I_{l}\left( R \mu _{1}\right) K_{l}\left( R_{\infty } \mu _{2}\right) \mu _{2}+R\left( I_{l}\left( R_{\infty } \mu _{2}\right) K_{l}\left( R \mu _{2}\right) \right. \right. \right. \\&-\left. \left. I_{l}\left( R \mu _{2}\right) K_{l}\left( R_{\infty } \mu _{2}\right) \right) \mu _{1}\left( I_{l-1}\left( R \mu _{1}\right) -\frac{l I_{l}\left( R \mu _{1}\right) }{R \mu _{1}}\right) \right. \\&+\left. \left. {D} I_{l}\left( R \mu _{1}\right) \left( R I_{l}\left( R_{\infty } \mu _{2}\right) \mu _{2}\left( K_{l-1}\left( R \mu _{2}\right) +\frac{l K_{l}\left( R \mu _{2}\right) }{R \mu _{2}}\right) -l I_{l}\left( R \mu _{2}\right) K_{l}\left( R_{\infty } \mu _{2}\right) \right) \right) \right) . \end{aligned}$$

The nutrient $\sigma$ on $\varGamma$ is given by

$$\begin{aligned} {} (\sigma )_{\varGamma }= & {} \left( A_{1} I_{0}\left( \mu _{1} r\right) +B_{1} I_{l}\left( \mu _{1} r\right) \delta e^{i l \theta }\right) _{\varGamma }\nonumber \\= & {} A_{1} I_{0}\left( \mu _{1} R\right) +\left( \mu _{1} A_{1} I_{1}\left( \mu _{1} R\right) +B_{1} I_{l}\left( \mu _{1} R\right) \right) \delta e^{i l \theta }. \end{aligned}$$

(77)

The normal derivative of $\sigma$ on $\varGamma$ is given by

$$\begin{aligned} \left( \frac{\partial \sigma }{\partial \mathbf {n}}\right) _{\varGamma }= & {} \left( \frac{\partial \sigma }{\partial r}\right) _{\varGamma } \nonumber \\= & {} \left( \left( A_{1} I_{0}\left( \mu _{1} r\right) +B_{1} I_{l}\left( \mu _{1} r\right) \delta e^{i l \theta }\right) _{r}\right) \nonumber \\= & {} \left( A_{1} \mu _{1} I_{1}\left( \mu _{1} r\right) +\left( B_{1} \mu _{1}\left( I_{l-1}\left( \mu _{1} r\right) -\frac{l}{\mu _{1} r} I_{l}\left( \mu _{1} r\right) \right) \right) \delta e^{i l \theta }\right) _{\varGamma }\nonumber \\= & {} \mu _{1} A_{1} I_{1}\left( \mu _{1} R\right) +\left( A_{1}\left( \mu _{1}^{2} I_{0}\left( \mu _{1} R\right) -\mu _{1} \frac{I_{1}\left( \mu _{1} R\right) }{R}\right) \right. \nonumber \\&\left. +B_{1}\left( \mu _{1} I_{l-1}\left( \mu _{1} R\right) -l \frac{I_{l}\left( \mu _{1} R\right) }{R}\right) \right) \delta e^{i l \theta }, \end{aligned}$$

(78)

where we use the identity in Eq. (6162),

$$\begin{aligned} I_{2}\left( \mu _{1} R\right) =2 I_{1}\left( \mu _{1} R\right) ^{\prime }-I_{0}\left( \mu _{1} R\right) =2\left( I_{0}\left( \mu _{1} R\right) -\frac{1}{\mu _{1} R} I_{1}\left( \mu _{1} R\right) \right) -I_{0}\left( \mu _{1} R\right) . \end{aligned}$$

Similarly, we seek a solution of Laplace equation, which reduces to Eq. (53) on the perturbed circle given by Eq. (55). It is sufficient to consider the expression

$$\begin{aligned} p=A+\delta e^{i l \theta } B r^{l}. \end{aligned}$$

(79)

For the perturbed circle defined by Eq. (55), $\kappa$ is given by

$$\begin{aligned} \kappa =\frac{1}{R}\left( 1+\frac{l^{2}-1}{R} \delta e^{i l \theta }\right) . \end{aligned}$$

(80)

On the interface from Eqs. (53),(55), and (77) we obtain

$$\begin{aligned} (p)_{\varGamma }= & {} A+B R^{l} \delta e^{i l \theta } \nonumber \\= & {} \mathscr {G}^{-1} \frac{1}{R}+\left( \mathscr {P}-\chi _{\sigma }\right) \left( A_{1} I_{0}\left( \mu _{1} R\right) \right) -\frac{\mathscr {A}}{2 d} R^{2}\nonumber \\&+\left( \mathscr {G}^{-1} \frac{l^{2}-1}{R^{2}}-\frac{\mathscr {A}}{d} R+\left( \mathscr {P}-\chi _{\sigma }\right) \left( A_{1} \mu _{1} I_{1}\left( \mu _{1} R\right) +B_{1} I_{l}\left( \mu _{1} R\right) \right) \right) \delta e^{i l \theta }.\nonumber \\ \end{aligned}$$

(81)

It is straightforward to derive that

$$\begin{aligned} A&=\mathscr {G}^{-1} \frac{1}{R}-\frac{\mathscr {A}}{2 d} R^{2}+\left( \mathscr {P}-\chi _{\sigma }\right) A_{1} I_{0}\left( \mu _{1} R\right) , \end{aligned}$$

(82)

$$\begin{aligned} B&=\left( \mathscr {G}^{-1} \frac{l^{2}-1}{R^{2}}-\frac{\mathscr {A}}{d} R+\left( \mathscr {P}-\chi _{\sigma }\right) \left( \mu _{1} A_{1} I_{1}\left( \mu _{1} R\right) +B_{1} I_{l}\left( \mu _{1} R\right) \right) \right) \frac{1}{R^{l}}. \end{aligned}$$

(83)

Thus,

$$\begin{aligned} p= & {} \mathscr {G}^{-1} \frac{1}{R}-\frac{\mathscr {A}}{2 d} R^{2}+\left( \mathscr {P}-\chi _{\sigma }\right) A_{1} I_{0}\left( \mu _{1} R\right) \nonumber \\&+\left( \mathscr {G}^{-1} \frac{l^{2}-1}{R^{2}}-\frac{\mathscr {A}}{d} R+\left( \mathscr {P}-\chi _{\sigma }\right) \left( \mu _{1} A_{1} I_{1}\left( \mu _{1} R\right) +B_{1} I_{l}\left( \mu _{1} R\right) \right) \right) \frac{r^{l}}{R^{l}} \delta e^{i l \theta }.\nonumber \\ \end{aligned}$$

(84)

The normal derivative of p is given by

$$\begin{aligned} \left( \frac{\partial p}{\partial \mathbf {n}}\right) _{\varGamma }= & {} \left( \frac{\partial p}{\partial r}\right) _{\varGamma }\nonumber \\= & {} l\left( \mathscr {G}^{-1} \frac{l^{2}-1}{R^{3}}{-}\frac{\mathscr {A}}{d}{+}\left( \mathscr {P} {-}\chi _{\sigma }\right) \left( \mu _{1} A_{1} \frac{I_{1}\left( \mu _{1} R\right) }{R}{+}B_{1} \frac{I_{l}\left( \mu _{1} R\right) }{R}\right) \right) \delta e^{i l \theta }.\nonumber \\ \end{aligned}$$

(85)

Note that

$$\begin{aligned} n \cdot (\mathbf {x})_{\varGamma }=r+O\left( \delta ^{2}\right) =R+\delta e^{i l \theta }+O\left( \delta ^{2}\right) . \end{aligned}$$

(86)

Combining (78),(85),(86) and (54), we obtain

$$\begin{aligned} V= & {} \frac{\mathrm{d}R}{\mathrm{d}t}+\frac{\mathrm{d}\delta }{\mathrm{d}t} e^{i l \theta } \nonumber \\= & {} -l\left( \mathscr {G}^{-1} \frac{l^{2}-1}{R^{3}}-\frac{\mathscr {A}}{d}+\left( \mathscr {P} -\chi _{\sigma }\right) \left( \mu _{1} A_{1} \frac{I_{1}\left( \mu _{1} R\right) }{R}+B_{1} \frac{I_l\left( \mu _{1} R\right) }{R}\right) \right) \delta e^{i l \theta }\nonumber \\&+\mathscr {P} \frac{\partial \sigma }{\partial r}-\frac{\mathscr {A}}{d}\left( R+\delta e^{i l \theta }\right) \nonumber \\= & {} -\frac{\mathscr {A} R}{d}+\mathscr {P} \frac{\partial \sigma }{\partial r}+\left( -\mathscr {G}^{-1} \frac{l\left( l^{2}-1\right) }{R^{3}}+\frac{l-1}{d} \mathscr {A}\right. \nonumber \\&\left. -l\left( \mathscr {P}-\chi _{\sigma }\right) \left( \mu _{1} A_{1} \frac{I_{1}\left( \mu _{1} R\right) }{R}+B_{1} \frac{I_{l}\left( \mu _{1} R\right) }{R}\right) \right) \delta e^{i l \theta }\nonumber \\= & {} - \frac{\mathscr {A} R}{d}+\mathscr {P}\left( \mu _{1} A_{1} I_{1}\left( \mu _{1} R\right) +\left( A_{1}\left( \mu _{1}^{2} I_{0}\left( \mu _{1} R\right) -\mu _{1} \frac{I_{1}\left( \mu _{1} R\right) }{R}\right) \right. \right. \nonumber \\&\left. \left. +B_{1}\left( \mu _{1} I_{l-1}\left( \mu _{1} R\right) -l \frac{I_{1}\left( \mu _{1} R\right) }{R}\right) \right) \delta e^{i l \theta }\right) \nonumber \\&+\left( -\mathscr {G}^{-1} \frac{l\left( l^{2}-1\right) }{R^{3}}+\frac{l-1}{d} \mathscr {A}-l\left( \mathscr {P}-\chi _{\sigma }\right) \left( \mu _{1} A_{1} \frac{I_{1}\left( \mu _{1} R\right) }{R}+B_{1} \frac{I_l\left( \mu _{1} R\right) }{R}\right) \right) \delta e^{i l \theta } \nonumber \\= & {} C \mathscr {P}-\frac{\mathscr {A} R}{d}+\nonumber \\&\left( -\mathscr {G}^{-1} \frac{l\left( l^{2}-1\right) }{R^{3}}+\frac{l-1}{d} \mathscr {A}+ \mathscr {P}\left( \mu _{1}^{2} A_{1} I_{0}\left( \mu _{1} R\right) +B_{1}\left( \mu _{1} I_{l-1}\left( \mu _{1} R\right) -\frac{l}{R} I_{l}\left( \mu _{1} R\right) \right) -\frac{{C}}{R}\right) \right. \nonumber \\&-\left. \left( \mathscr {P}-\chi _{\sigma }\right) \left( B_{1} \frac{l}{R} I_{l}\left( \mu _{1} R\right) +\frac{l}{R} {C}\right) \right) \delta e^{i l \theta } , \end{aligned}$$

(87)

where $C=\mu _{1} A_{1} I_{1}\left( \mu _{1} R\right)$.

Equating coefficients of like harmonics, we obtain

$$\begin{aligned} \frac{\mathrm{d}R}{\mathrm{d}t}=C \mathscr {P}-\frac{\mathscr {A} R}{d}, \end{aligned}$$

(88)

$$\begin{aligned} R^{-1}{\frac{{\mathrm{d}R}}{{\mathrm{d}t}}}=\frac{C \mathscr {P}}{R}-\frac{\mathscr {A}}{d}, \end{aligned}$$

(89)

and

$$\begin{aligned} \delta ^{-1}\frac{\mathrm{d}\delta }{\mathrm{d}t}= & {} -\mathscr {G}^{-1} \frac{l\left( l^{2}-1\right) }{R^{3}}+\frac{l-1}{d} \mathscr {A}\nonumber \\&+ \mathscr {P}\left( \mu _{1}^{2} A_{1} I_{0}\left( \mu _{1} R\right) +B_{1}\left( \mu _{1} I_{l-1}\left( \mu _{1} R\right) -\frac{l}{R} I_{l}\left( \mu _{1} R\right) \right) -\frac{{C}}{R}\right) \nonumber \\&-\left( \mathscr {P}-\chi _{\sigma }\right) \left( \mu _{1} B_{1} \frac{l}{R} I_{l}\left( \mu _{1} R\right) +\frac{l}{R} {C}\right) . \end{aligned}$$

(90)

The equation of shape perturbation is given by

$$\begin{aligned} \left( \frac{\delta }{R}\right) ^{-1} \frac{\mathrm{d}}{\mathrm{d}t}{\left( \frac{\delta }{R}\right) }= & {} \delta ^{-1}\frac{\mathrm{d}\delta }{\mathrm{d}t}-R^{-1}\frac{\mathrm{d}R}{\mathrm{d}t}\nonumber \\= & {} -\mathscr {G}^{-1} \frac{l\left( l^{2}-1\right) }{R^{3}}+\frac{l}{d} \mathscr {A}\nonumber \\&+\mathscr {P}\left( \mu _{1}^{2} A_{1} I_{0}\left( \mu _{1} R\right) +B_{1}\left( \mu _{1} I_{l-1}\left( \mu _{1} R\right) -\frac{l}{R} I_{l}\left( \mu _{1} R\right) \right) -\frac{2}{R} {C}\right) \nonumber \\&-\left( \mathscr {P}-\chi _{\sigma }\right) \left( B_{1} \frac{l}{R} I_{l}\left( \mu _{1} R\right) +\frac{l}{R} C\right) . \end{aligned}$$

(91)

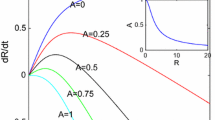
The critical apoptosis parameter $\mathscr {A}_{c}$ is the function of R such that $\frac{\mathrm{d}}{\mathrm{d}t}{\left( \frac{{\delta }}{R}\right) }=0$ and is given by

$$\begin{aligned} \mathscr {A}_{c}= & {} \mathscr {G}^{-1} \frac{d\left( l^{2}-1\right) }{R^{3}} -\mathscr {P} \frac{d}{l}\left( \mu _{1}^{2} A_{1} I_{0}\left( \mu _{1} R\right) +B_{1}\left( \mu _{1} I_{l-1}\left( \mu _{1} R\right) -\frac{l}{R} I_{l}\left( \mu _{1} R\right) \right) -\frac{2}{R} {C}\right) \nonumber \\&+\left( \mathscr {P}-\chi _{\sigma }\right) \frac{d}{l}\left( B_{1} \frac{l}{R} I_{l}\left( \mu _{1} R\right) +\frac{l}{R} {C}\right) . \end{aligned}$$

(92)

Appendix B: The Evaluation of the Boundary Integrals

With the integral formulation above, we assume interface curves $\varGamma$ and $\varGamma _{\infty }$ are analytic and given by $\big \{\mathbf {x}(\alpha ,t)=(x(\alpha ,t),y(\alpha ,t): 0\le \alpha \le 2 \pi \big \}$, where $\mathbf {x}$ is $2 \pi$-periodic in the parametrization $\alpha$. The unit tangent and normal (outward) vectors can be calculated as $\mathbf {s}=(x_\alpha ,y_\alpha )/s_\alpha$, $\mathbf {n}=(y_\alpha ,-x_\alpha )/s_\alpha$, where the local variation of the arclength $s_\alpha =\sqrt{x_\alpha ^2+y_\alpha ^2}$. Subscripts refer to partial differentiation. We track the interfaces $\varGamma$ and $\varGamma _{\infty }$ by introducing N marker points to discretize the planar curves, parametrized by $\alpha _j=jh$, $h=\frac{2\pi }{N}$, N is a power of 2. Here, we focus on the numerical evaluation of integrals following Jou et al. (1997), Li and Li (2011), Lu et al. (2019). A rigorous convergence and error analysis of the boundary integral method for a simplified tumor problem can be found in Hao et al. (2018).

Computation of the single-layer potential-type integral

In Eqs. (35), (36), (37) and (42), the single-layer potential-type integrals contain the Green functions with a logarithmic singularity at $r=0$. They can be rewritten in the following form under the parametrization $\alpha$

$$\begin{aligned} \int _{\varGamma } \Phi (\alpha ,\alpha ')\phi (\alpha ')s_{\alpha }(\alpha ')\mathrm{d}\alpha ', \end{aligned}$$

(93)

where $\Phi$ are the Green functions G or $G_i$ , $\varGamma$ may be either $\varGamma$ or $\varGamma _{\infty }$ and $\phi$ may be $\eta$ ,$\frac{\partial \sigma _1}{\partial \mathbf {n}}$ or $\frac{\partial \sigma _2}{\partial \mathbf {n}_\infty }$. We may decompose the Green functions as below

$$\begin{aligned} G(\alpha ,\alpha ')= & {} -\frac{1}{2 \pi } \ln r =-\frac{1}{2\pi }\left( \ln {2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| } +\left[ \ln r-\ln {2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| }\right] \right) ,\nonumber \\ \end{aligned}$$

(94)

$$\begin{aligned} G_{i}(\alpha ,\alpha ')= & {} \frac{1}{2 \pi } K_{0}(\mu _{i} r)= -\frac{1}{2 \pi } \left( I_{0}(\mu _{i}r)\ln {2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| }\right. \nonumber \\&\left. +\left[ -K_{0}(\mu _{i}r) -I_{0}(\mu _{i}r)\ln {2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| } \right] \right) , \end{aligned}$$

(95)

where $I_{0}$ is a modified Bessel function of the first kind, $r=|\mathbf {x}(\alpha )-\mathbf {x}'(\alpha ')|$. The square brackets on the right-hand side of Eqs. (94), (95) have removable singularity at $\alpha =\alpha '$, since $r= s_{\alpha }\left| \alpha -\alpha '\right| \sqrt{1+\mathcal {O}(\alpha -\alpha ')} =s_{\alpha }\left| \alpha -\alpha '\right| (1+\mathcal {O}(\alpha -\alpha '))$ for $\alpha \approx \alpha '$, where $\mathcal {O}{(\alpha -\alpha ')}$ denotes a smooth function that vanishes as $\alpha \rightarrow \alpha '$, and since $K_0$ has the expansion

$$\begin{aligned} K_{0}(z)=-\left( \log \frac{z}{2}+C\right) I_{0}(z)+\Sigma _{n=1}^{\infty } \frac{\psi (n)}{(n !)^{2}}\left( \frac{z}{2}\right) ^{2 n}. \end{aligned}$$

(96)

Thus, for an analytic and $2\pi$-periodic function $f(\alpha ,\alpha ')$, a standard trapezoidal rule or alternating point rule can be used to evaluate the integral

$$\begin{aligned} \int _{0}^{2\pi } f(\alpha ,\alpha ') \ln {\frac{r}{2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| }} \mathrm{d}\alpha '. \end{aligned}$$

(97)

The remaining terms on the right-hand side of Eqs. (94), (95) have logarithmic singularity and can be evaluated through the following spectrally accurate quadrature Kress (1995)

$$\begin{aligned} \int _{0}^{2\pi }f(\alpha _i,\alpha ') \ln {2 \left| \sin {\frac{\alpha _i-\alpha '}{2}}\right| } \mathrm{d}\alpha '\approx \Sigma _{j=0}^{2m-1}q_{\left| j-i\right| }f(\alpha _i,\alpha _j), \end{aligned}$$

(98)

where $m=\frac{N}{2}$, $\alpha _i=\frac{\pi i}{m}$ for $i=0,1,\ldots ,2m-1$, and weight coefficients

$$\begin{aligned} q_j=-\frac{\pi }{m}\Sigma _{k=1}^{m-1}\frac{1}{k}\cos {\frac{kj\pi }{m}}-\frac{(-1)^j\pi }{2m^2} , \text {for } j=0,1,\ldots ,2m-1. \end{aligned}$$

(99)

The derivative $\frac{d}{ds}$ in Eq. (42) is approximated using fast Fourier transform spectral derivatives, thus maintaining spectral accuracy.

Computation of the double-layer potential-type integral

In Eqs. (35), (36), (37) and (41), the double-layer potential-type integrals contain the Green functions with singularity at $r=0$ (logarithmic for Eqs. (35), (36), (37)). They can be rewritten as in the following form under the parametrization $\alpha$

$$\begin{aligned} \int _{\varGamma } \frac{\partial \Phi (\alpha ,\alpha ')}{\partial \mathbf {n}(\alpha ')}\phi (\alpha ')s_{\alpha }(\alpha ')\mathrm{d}\alpha ', \end{aligned}$$

(100)

where $\Phi$ are the Green functions G or $G_i$, $\varGamma$ may be either $\varGamma$ or $\varGamma _{\infty }$ and $\phi$ may be $\eta$, $\sigma _1$ or $\sigma _2=1$. Further,

$$\begin{aligned} \frac{\partial G(\alpha ,\alpha ')}{\partial \mathbf {n}(\alpha ')}s_{\alpha }(\alpha ')= h(\alpha ,\alpha ')\frac{1}{r}, \end{aligned}$$

(101)

where the auxiliary function $h(\alpha ,\alpha ')=\frac{(\mathbf {x}(\alpha )-\mathbf {x}(\alpha '))\cdot \mathbf {n}(\alpha ')s_\alpha (\alpha ')}{2\pi r}$ with $r=\left| \mathbf {x}(\alpha )-\mathbf {x}(\alpha ')\right|$. Note that $h(\alpha ,\alpha ')\sim \mathcal {O}(\alpha -\alpha ')$. Since $\frac{\partial G}{\partial \mathbf {n}}$ has no logarithmic singularity, we may simply use the alternating point rule to evaluate it. For $\frac{\partial G_i}{\partial \mathbf {n}}$, we decompose it as below

$$\begin{aligned} \frac{\partial G_{i}(\alpha ,\alpha ')}{\partial \mathbf {n}(\alpha ')}s_{\alpha }(\alpha ')= h(\alpha ,\alpha ') K_{1}(\mu _{i} r)= g_1(\alpha ,\alpha ')\ln {2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| } +g_2(\alpha ,\alpha '), \end{aligned}$$

(102)

where $g_1(\alpha ,\alpha ')$ and $g_2(\alpha ,\alpha ')$ are analytic and $2\pi$-periodic functions with

$$\begin{aligned} g_1(\alpha ,\alpha ')= & {} h(\alpha ,\alpha ')I_1(\mu _i r), \end{aligned}$$

(103)

$$\begin{aligned} g_2(\alpha ,\alpha ')= & {} h(\alpha ,\alpha ') \left[ K_{1}(\mu _{i}r) -I_{1}(\mu _{i}r)\ln {2 \left| \sin {\frac{\alpha -\alpha '}{2}}\right| } \right] , \end{aligned}$$

(104)

where we have used the fact

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}r}K_0(r)=-K_1(r). \end{aligned}$$

(105)

Since $K_1$ has the expansion

$$\begin{aligned} K_{1}(z)=\frac{1}{z}+\left( \log \frac{z}{2}+C\right) I_{1}(z)-\frac{1}{2} \sum _{n=0}^{\infty } \frac{\psi (n+1)+\psi (n)}{n !(n+1) !}\left( \frac{z}{2}\right) ^{2 n+1}, \end{aligned}$$

(106)

the square bracket on the right-hand side of Eq. (104) also has removable singularity at $\alpha =\alpha '$, and thus, the integral involving $g_2(\alpha ,\alpha ')$ can be evaluated by a standard trapezoidal rule or alternating point rule. Note that

$$\begin{aligned} g_2(\alpha ,\alpha )=\frac{h(\alpha ,\alpha )}{\mu _i r}=\frac{1}{4\pi \mu _i} \frac{x_\alpha y_{\alpha \alpha }-x_{\alpha \alpha }y_\alpha }{x_\alpha ^2+y_\alpha ^2}. \end{aligned}$$

(107)

The first term on the right-hand side of Eq. (102) is still singular and evaluated through the quadrature given in Eqs. (98), and (99).

To summarize, using Nyström discretization with the Kress quadrature rule described above, we reduce the boundary integral Eqs. (35), (36), (37) and (41) to two dense linear systems with the unknowns as the discretization of $\eta$ , $\sigma _1$, $\frac{\partial \sigma _1}{\partial \mathbf {n'}}$ on $\varGamma$ and $\frac{\partial \sigma _2}{\partial \mathbf {n'_\infty }}$ on $\varGamma _\infty$, which can be solved using an iterative solver, e.g., GMRES Saad and Schultz (1986).

Appendix C: The Evolution of the Interface

As indicated by Hou et al. (1994), the curvature-driven motion introduces high-order derivatives, both non-local and nonlinear, into the dynamics through the Laplace–Young condition at the interface. Explicit time integration methods thus suffer from severe stability constraints, and implicit methods are difficult to apply since the stiffness enters nonlinearly. Hou et al. resolved these difficulties by adopting the $\theta -L$ formulation and the small-scale decomposition (SSD), which we apply here.

$\theta -L$ formulation

This formulation helps to circumvent the problem of point clustering. Consider a point $\mathbf {x}(\alpha ,t)=(x(\alpha ,t),y(\alpha ,t))\in \varGamma (t)$. Denote the unit tangent and normal (outward) vectors as $\hat{\mathbf {s}}=(x_\alpha ,y_\alpha )/s_\alpha$ and $\hat{\mathbf {n}}=(y_\alpha ,-x_\alpha )/s_\alpha$, the normal velocity and tangent velocity by $V(\alpha ,t)=u\cdot \hat{\mathbf {n}}$ and $T(\alpha ,t)=u\cdot \hat{\mathbf {s}}$, respectively, where $u=\mathbf {x}_t=V \hat{\mathbf {n}}+T \hat{\mathbf {s}}$ gives the motion of $\varGamma (t)$. The tangent angle that the planar curve $\varGamma (t)$ forms with the horizontal axis at $\mathbf {x}$, called $\theta$, satisfies $\theta =\tan ^{-1}{\frac{y_\alpha }{x_\alpha }}$. The length of one period of the curve is $L(t)=\int _0^{2\pi }s_\alpha \mathrm{d}\alpha$, where $s_\alpha$, the derivative of the arclength, satisfies $s_\alpha ^2=x_\alpha ^2+y_\alpha ^2$. Differentiating these two equations in time, we obtain the following evolution equations:

$$\begin{aligned} \theta _t= & {} \kappa T - V_s=\frac{1}{s_\alpha }(\theta _\alpha T- V_\alpha ), \end{aligned}$$

(108)

$$\begin{aligned} s_{\alpha t}= & {} (T_s+\kappa V)s_\alpha =T_\alpha +\theta _\alpha V. \end{aligned}$$

(109)

Instead of using the (x, y) coordinates, $(L,\theta )$ becomes the dynamical variables. The unit tangent and normal vectors become $\hat{\mathbf {s}}=(\cos {\theta },\sin {\theta })$, $\hat{\mathbf {n}}=(\sin {\theta },-\cos {\theta })$.

The normal velocity V is calculated using Eq. (30). The tangent velocity T is chosen (independent of the morphology of the interface) such that the marker points are equally spaced in arclength to prevent point clustering:

$$\begin{aligned} T(\alpha ,t)= \frac{\alpha }{2\pi }\int _0^{2\pi }\theta _{\alpha '}V' \mathrm{d}\alpha '-\int _0^\alpha \theta _{\alpha '}V' \mathrm{d}\alpha '. \end{aligned}$$

(110)

It follows that $s_\alpha$ is independent of $\alpha$ and thus is everywhere equal to its mean:

$$\begin{aligned} s_\alpha =\frac{1}{2\pi }\int _0^{2\pi }s_\alpha (\alpha ,t)\mathrm{d}\alpha =\frac{L(t)}{2\pi }. \end{aligned}$$

(111)

The procedure for obtaining the initial equal arclength parametrization is presented in “Appendix B” of Baker and Shelley (1990). The idea is to solve the nonlinear equation

$$\begin{aligned} \int _0^{\alpha _j} s_{\beta }d\beta =\frac{j}{N}L \end{aligned}$$

(112)

for $\alpha _j$ using Newton’s method and evaluate the equal arclength marker points $\mathbf {x}(\alpha _j)$ by interpolation in Fourier space. We may recover the interface by simply integrating:

$$\begin{aligned} \mathbf {x}_\alpha =\mathbf {x}_s s_\alpha =\frac{L(t)}{2\pi }(\cos {\theta (\alpha ,t)},\sin {\theta (\alpha ,t)}). \end{aligned}$$

(113)

Small-scale decomposition (SSD)

The idea of the small scale decomposition (SSD) is to extract the dominant part of the equations at small spatial scales Hou et al. (1994). To remove the stiffness, we use SSD in our problem and develop an explicit, non-stiff time integration algorithm. In Eqs. (35), (36), (37), (41) and (42), based on the analysis of the single-layer- and double-layer-type terms, the only singularity in the integrands comes from the logarithmic kernel. Following Hou et al. (1994) and noticing the curvature term in Eq. (41), one can show that at small spatial scales,

$$\begin{aligned} V(\alpha ,t) \sim \frac{1}{s_\alpha ^2} \mathscr {H}[\theta _{\alpha \alpha }], \end{aligned}$$

(114)

where $\mathscr {H}(\xi )=\frac{1}{2\pi }\int _0^{2\pi }\xi '\cot {\frac{\alpha -\alpha '}{2}}\mathrm{d}\alpha '$ is the Hilbert transform for a $2\pi$-periodic function $\xi$.

We rewrite Eq. (108),

$$\begin{aligned} \theta _t=\frac{1}{s_\alpha ^3} \mathscr {H}[\theta _{\alpha \alpha \alpha }]+N(\alpha ,t), \end{aligned}$$

(115)

where the Hilbert transform term is the dominating high-order term at small spatial scales, and $\displaystyle N= (\kappa T-V_s)-\frac{1}{s_\alpha ^3} \mathscr {H}[\theta _{\alpha \alpha \alpha }]$ contains other lower-order terms in the evolution. This demonstrates that an explicit time-stepping method has the high-order constraint $\displaystyle \varDelta t \le \left( \frac{h}{s_\alpha } \right) ^3$ where $\varDelta t$ and h are the time-step and spatial grid size, respectively. This has been demonstrated numerically in the seminal work Hou et al. (1994) for a Hele-Shaw problem. For the tumor growth problem, the semi-implicit time-stepping scheme (see Eq. (115)) requires $\varDelta t = O(h)$ instead of explicit schemes which would require $\varDelta t = O(h^3)$. In Sect. 5.1, we show a numerical example using $N=1024$ to simulate a twofold tumor. In this simulation, we could use $\varDelta t$ as large as $\varDelta t=1.0 \times 10^{-2}$ for stability instead of $\varDelta t<10^{-6}$ for an explicit scheme with the equal arclength parametrization. For the purpose of numerical accuracy, we used a smaller time step in our simulation.

Appendix D: Semi-implicit Time-Stepping Scheme

Taking the Fourier transform of Eq. (115), we get

$$\begin{aligned} {\hat{\theta }}_t=-\frac{|k|^3}{s_\alpha ^3} {\hat{\theta }}(k,t) +{\hat{N}}(k,t). \end{aligned}$$

(116)

We solve Eq. (116) using the second-order accurate linear propagator method in the Adams–Bashforth form Hou et al. (1994) in Fourier space and apply the inverse Fourier transform to recover $\theta$. Specifically, we discretize Eq. (116) as

$$\begin{aligned} {\hat{\theta }}^{n+1}(k)=e_k(t_n,t_{n+1}){\hat{\theta }}^{n}(k)+\frac{\varDelta t}{2}(3e_k(t_n,t_{n+1}){\hat{N}}^{n}(k)-e_k(t_{n-1},t_{n+1}){\hat{N}}^{n-1}(k), \end{aligned}$$

(117)

where the superscript n denotes the numerical solutions at $t=t_n$ and the integrating factor

$$\begin{aligned} e_k(t_1,t_2)=\exp \left( -{|k|^3}\int _{t_1}^{t_2}\frac{\mathrm{d}t}{s_\alpha ^3(t)}\right) . \end{aligned}$$

(118)

Note that by setting the integrating factors in Eq. (117) to 1, we recover the Adams–Bashforth explicit time-stepping method. The integrating factors in Eq. (117) can be evaluated simply using the trapezoidal rule,

$$\begin{aligned} \int _{t_n}^{t_{n+1}}\frac{\mathrm{d}t}{s_\alpha ^3(t)}\approx & {} \frac{\varDelta t}{2} \left( \frac{1}{(s_\alpha ^n)^3}+\frac{1}{(s_\alpha ^{n+1})^3} \right) \nonumber , \\ \int _{t_{n-1}}^{t_{n+1}}\frac{\mathrm{d}tt}{s_\alpha ^3(t)}\approx & {} {\varDelta t} \left( \frac{1}{2(s_\alpha ^{n-1})^3}+\frac{1}{(s_\alpha ^{n})^3}+\frac{1}{2(s_\alpha ^{n+1})^3} \right) . \end{aligned}$$

(119)

To compute the arclength $s_\alpha$, equation (109) is discretized using the explicit second-order Adams–Bashforth method Hou et al. (1994),

$$\begin{aligned} s_\alpha ^{n+1}=s_\alpha ^n+\frac{\varDelta t}{2}(3M^n-M^{n-1}), \end{aligned}$$

(120)

where M is calculated using

$$\begin{aligned} M=\frac{1}{2\pi }\int _0^{2\pi }V(\alpha ,t)\theta _\alpha \mathrm{d}\alpha . \end{aligned}$$

(121)

Note that the second-order linear propagator and Adams–Bashforth methods are multi-step method and require two previous time steps. The first time step is realized using an explicit Euler method for $s_\alpha ^1$ and a first-order linear propagator of a similar form for $\hat{\theta }^1$.

Fig. 13

Tumor morphologies with different symmetric far-field geometries in the nutrient-poor regime ($D=1$). The far-field boundaries are $R_\infty =13+2\cos (k\theta ),k=3,4,5,6$ (Rows 1,3); $R_\infty =13+2\cos (k\theta -\pi /2),k=3,5,~R_\infty =13+2\cos (k\theta -\pi ),k=4,6$ (Rows 2,4). The initial tumor boundaries are $r=2.0+ 0.1\cos (2 \theta )$ (Rows 1,2); and $\frac{x^2}{2.1^2}+\frac{y^2}{1.9^2}=1$ (Rows 3,4). The remaining parameters are $\lambda =0.01$, $\chi _{\sigma }=10$, $\mathscr {P}=0.5$, $\mathscr {A}=0$, $\mathscr {G}^{-1}=0.001$. Here, $N=512$, and $\varDelta t=0.005$ (Color figure online)

To reconstruct the tumor–host interface $(x(\alpha ,t_{n+1}),y(\alpha ,t_{n+1}))$ from the updated $\theta ^{n+1}(\alpha )$ and $s_\alpha ^{n+1}$, we first update a reference point $(x(0,t_{n+1}),y(0,t_{n+1})$ using a second-order explicit Adams–Bashforth method to discretize the equation of motion $\mathbf {x}_t=V\hat{\mathbf {n}}$ with the tangential part dropped since it does not change the morphology:

$$\begin{aligned} (x(0,t_{n+1}),y(0,t_{n+1}))= & {} (x(0,t_{n}),y(0,t_{n}))\nonumber \\&+\frac{\varDelta t}{2} \left( 3V(0,t_n)\hat{\mathbf {n}}(0,t_{n})-V(0,t_{n-1})\hat{\mathbf {n}}(0,t_{n-1}) \right) .\nonumber \\ \end{aligned}$$

(122)

Once we update the reference point, we obtain the configuration of the interface from the $\theta ^{n+1}(\alpha )$ and $s_\alpha ^{n+1}$ by integrating Eq. (113) following Hou et al. (1994):

$$\begin{aligned} x(\alpha ,t_{n+1})= & {} x(0,t_{n+1})+s_\alpha ^{n+1}\left( \int _0^{\alpha } \cos (\theta ^{n+1}(\alpha '))\mathrm{d}\alpha ' -\frac{\alpha }{2\pi }\int _0^{2\pi }\cos (\theta ^{n+1}(\alpha '))\mathrm{d}\alpha '\right) ,\nonumber \\ y(\alpha ,t_{n+1})= & {} y(0,t_{n+1})+s_\alpha ^{n+1}\left( \int _0^{\alpha } \sin (\theta ^{n+1}(\alpha '))\mathrm{d}\alpha ' -\frac{\alpha }{2\pi }\int _0^{2\pi }\sin (\theta ^{n+1}(\alpha '))\mathrm{d}\alpha '\right) ,\nonumber \\ \end{aligned}$$

(123)

where the indefinite integration is performed using the discrete Fourier transform.

We use a 25th-order Fourier filter to damp the highest nonphysical mode and suppress the aliasing error Hou et al. (1994). We also use Krasny filtering Krasny (1986) to prevent the accumulation of round-off errors during the computation.

We solve first the nutrient field $\sigma$ and then the pressure field p. Next we compute the normal velocity V and update the interface $\varGamma (t)$ and repeat this procedure.

Appendix E

In Fig. 13, we present tumor morphologies at similar sizes under the same growth conditions but using different symmetric far-field boundaries: $R_\infty =13+2\cos (k\theta ),k=3,4,5,6$ (Row 1,3) and $R_\infty =13+2\cos (k\theta -\pi /2),k=3,5,R_\infty =13+2\cos (k\theta -\pi ),k=4,6$ (Row 2,4). The parameters are the same as in Fig. 7 in the main text, where $\chi _\sigma =5$, except that here in Fig. 13 we use $\chi _\sigma =10$. As in Fig. 7, initial tumor boundary in rows 1 and 2 is the perturbed circle $R_\infty =2.0+ 0.1\cos (2 \theta )$ while in rows 3 and 4 the initial tumor boundary is the ellipse $\frac{x^2}{2.1^2}+\frac{y^2}{1.9^2}=1$. Hence, by comparing the evolution within each row, and between rows 1 and 2 and rows 3 and 4, we can see the effect of the far-field boundary shapes. By comparing rows 1 and 3 and rows 2 and 4, we can see the effect of the different initial shapes.

The results are similar to those obtained in Fig. 7 although here, because the chemotaxis coefficient $\chi _\sigma$ is increased, the tubular structures develop faster and are narrower than those observed in Fig. 7. In particular, when the initial condition is the perturbed circle (rows 1 and 2), the far-field geometry has limited influence on tumor morphologies consistent with that observed in Figs. 5 and 6. However, when the initial condition is an ellipse, which contains many modes, the morphologies are much more sensitive to the far-geometry because of the instability.