A Next-Generation Approach to Calculate Source–Sink Dynamics in Marine Metapopulations

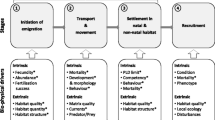
Abstract

In marine systems, adult populations confined to isolated habitat patches can be connected by larval dispersal. Source–sink theory provides effective tools to quantify the effect of specific habitat patches on the dynamics of connected populations. In this paper, we construct the next-generation matrix for a marine metapopulation and demonstrate how it can be used to calculate the source–sink dynamics of habitat patches. We investigate the effect of environmental variables on the source–sink dynamics and demonstrate how the next-generation matrix can provide useful biological insight into transient as well as asymptotic dynamics of the model.

Derivation from McKendrick–von Foerster PDE

Here, we derive Eq. 1 by solving the McKendrick–von Foerster PDE:

$$\begin{aligned} \frac{\partial n_{k}^{i}(t,a)}{\partial t}+\frac{\partial n_{k}^{i}(t,a)}{\partial a}&=-\mu _{k}^{i}(a)n_{k}^{i}(t,a)\nonumber \\ n_{k}^{i}(t,0)&=B_{k}^{i}(t)\nonumber \\ n_k^i(0,a)&={\tilde{n}}_k^i(a)\nonumber \\ \mu _{k}^{i}(a)&=-\frac{{\left( M_{k}^{i}(a)S_{k}^{i}(a)\right) }^{\prime }}{M_{k}^{i}(a)S_{k}^{i}(a)}. \end{aligned}$$

(14)

First, for simplicity we drop the indexes k and i so that $n_k^i(t,a)=n(t,a)$. Then, we solve this linear partial differential equation using the method of characteristics. The goal is to reduce the partial differential equation into an ordinary differential equation of one variable along certain characteristic curves in a and t. To do this, we parameterize $a=a(s)$ and $t=t(s)$, so that n(t(s), a(s)) is now a function of the single variable s. Differentiating n(t(s), a(s)) with respect to s:

$$\begin{aligned} \frac{{\hbox {d}}n}{{\hbox {d}}s}=\frac{\partial n}{\partial t}\frac{{\hbox {d}}t}{{\hbox {d}}s}+\frac{\partial n}{\partial a }\frac{{\hbox {d}}a}{{\hbox {d}}s}. \end{aligned}$$

(15)

Now we choose the characteristic curves a(s) and t(s) such that

$$\begin{aligned} \frac{{\hbox {d}}a}{{\hbox {d}}s}=1 \quad \text {and} \quad \frac{{\hbox {d}}t}{{\hbox {d}}s}=1. \end{aligned}$$

Then, substituting Eq. 14 into Eq. 15 we arrive at the ordinary differential equation:

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}s}n(t(s),a(s))=-\mu (a(s))n(t(s),a(s)). \end{aligned}$$

(16)

Solving for the characteristic curves, t(s) and a(s), we find

$$\begin{aligned} t(s)=s+t_0\quad \text {and} \quad a(s)=s+a_0. \end{aligned}$$

Then, solving for n(t(s), a(s)) in Eq. 16 we find:

$$\begin{aligned} n(t(s),a(s))&=n(t(0),a(0))e^{-\int _0^s\mu (x+a_0)dx}{\text{ d }x}\nonumber \\&=n(t(0),a(0))e^{-\int _{a_0}^{a_0+s}\mu (y)dy}\nonumber \\&=n(t(0),a(0))e^{\int _{a_0}^{a_0+s}\frac{{\left( M(y)S(y)\right) }^{\prime }}{M(y)S(y)}dy}\nonumber \\&=n(t(0),a(0))e^{\int _{a_0}^{a_0+s} \frac{d}{dy}\log (M(y)S(y))dy}\nonumber \\&=n(t(0),a(0))\frac{M(a_0+s)S(a_0+s)}{M(a_0)S(a_0)}. \end{aligned}$$

(17)

Now we have two boundary conditions to impose, one at $t=0$ and one at $a=0$. Together, the two boundaries intersect all characteristic curves, and so Eq. 17 is the unique solution to Eq. 14 for all $a\ge$, $t\ge 0$. From the form of our characteristic equations for a(s) and t(s), it is clear that all characteristics are lines $t=a+b$ in the a-t plane. The line $t=a$ divides the a-t plane into two regions: $t\le a$ and $t>a$. Characteristic curves for which $t\le a$ intersect the boundary $t=0$ at some point $(t,a)=(0,a_0)$. Substituting $t=s$ and $a=s+a_0$ into Eq. 17, we find

$$\begin{aligned} n(t,a)&=n(0,a-t)\frac{M(a)S(a)}{M(a-t)S(a-t)}\\&=n_0(a-t)\frac{M(a)S(a)}{M(a-t)S(a-t)}. \end{aligned}$$

Similarly, characteristic curves for which $t>a$ intersect the $a=0$ boundary at some point $(t,a)=(t_0,0)$. Substituting $t=s+t_0$ and $a=s$ into Eq. 17, we find

$$\begin{aligned} n(t,a)&=n(t-a,0)M(a)S(a)\\&=B(t-a)M(a)S(a). \end{aligned}$$

Therefore, together we have

$$\begin{aligned} n(t,a)={\left\{ \begin{array}{ll}B(t-a)M(a)S(a) &{}{} t>a \\ n_0(a-t)\frac{M(a)S(a)}{M(at) S(a-t)} &{}{} 0<t<a.\\ n_0(a) &{}{} t=0\end{array}\right. } \end{aligned}$$