A Spatially Resolved and Quantitative Model of Early Atherosclerosis

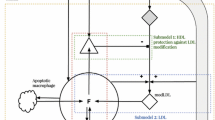
Abstract

Atherosclerosis is a major burden for all societies, and there is a great need for a deeper understanding of involved key inflammatory, immunological and biomechanical processes. A decisive step for the prevention and medical treatment of atherosclerosis is to predict what conditions determine whether early atherosclerotic plaques continue to grow, stagnate or become regressive. The driving biological and mechanobiological mechanisms that determine the stability of plaques are yet not fully understood. We develop a spatially resolved and quantitative mathematical model of key contributors of early atherosclerosis. The stability of atherosclerotic model plaques is assessed to identify and classify progression-prone and progression-resistant atherosclerotic regions based on measurable or computable in vivo inputs, such as blood cholesterol concentrations and wall shear stresses. The model combines Darcy’s law for the transmural flow through vessels walls, the Kedem–Katchalsky equations for endothelial fluxes of lipoproteins, a quantitative model of early plaque formation from a recent publication and a novel submodel for macrophage recruitment. The parameterization and analysis of the model suggest that the advective flux of lipoproteins through the endothelium is decisive, while the influence of the advective transport within the artery wall is negligible. Further, regions in arteries with an approximate wall shear stress exposure below 20% of the average exposure and their surroundings are potential regions where progression-prone atherosclerotic plaques develop.

Appendices

Appendix A Quantification of Model Parameters

In this section, a complete set of parameters for the spatially resolved model in SI units $\mathrm {mm}$, $\mathrm {g}$ and $\mathrm {h}$ is derived. Due to a lack of uniform experimental data, we do not distinguish between experimental results gained from the study of different animal models. As the media is the predominant part of the intima–media domain (Fok 2016; Hoffman et al. 2017; Yang and Vafai 2006; Prosi et al. 2005), we use parameters that correspond to the media.

1.1 Appendix A.1 Macrophage-Related Parameters

The parameters of the submodel of monocyte adhesion least-squares fitted to the experimental results by Jeng et al. (1993) are

$$\begin{aligned} \begin{aligned} P_{m}&= 443.17 \frac{1}{\mathrm {h}\;0.1452 \; \mathrm {mm}^2} = 3052.13 \frac{1}{\mathrm {h}\; \mathrm {mm}^2},\quad \delta _{m}= 68.62 \% , \\ k_{m}&= 7.09 \cdot 10^{-3} \; \frac{{\upmu } \mathrm {g}\; \mathrm {lipid \; protein}}{\mathrm {ml}} \,\widehat{=}\, 7.38\cdot 10^{6} \; \frac{1}{\mathrm {mm}^3}, \quad \delta _\tau = 40.22 \% , \\ \xi _\tau&= 1.95 \;\frac{\mathrm {dyn}}{\mathrm {cm}^2} = 1.95 \cdot 10^{-1} \;\mathrm {Pa},\quad \nu _\tau = 1.18, \end{aligned} \end{aligned}$$

(22)

where all values are given in the unit of the experiment and SI units. The conversion of $k_{m}$ from ${\upmu } \mathrm {g}\; \mathrm {lipid \; protein}$ to SI units is performed using $\rho _{10}=1.04 \cdot 10^{9}\; \frac{1}{{\upmu } \mathrm {g}\; \mathrm {lipid \; protein}}$ from Thon et al. (2018), Table 1. An overview of the least-squares fits is shown in Fig. 10a. Since intracellular free and esterified cholesterol can only diffuse within macrophages, the macrophages’ effective diffusion coefficient is also employed for the cholesterols, i.e., $D_{\mathrm {Eff},{m}} =D_{\mathrm {Eff},{f}}=D_{\mathrm {Eff},{b}} =3.6 \cdot 10^{-6} \; \frac{\mathrm {mm}^2}{\mathrm {h}}$, cf. Cilla et al. (2014) and Friedman and Hao (2015).

Fig. 10

Least-squares fits of a simulated monocyte adhesion $m(T_\mathrm {Adh})$ to experimental results by Jeng et al. (1993), Table 1, b filtration reflection coefficient $\sigma _{\mathrm {F},i}$ to results by Karner et al. (2001), Table 3, c hindrance coefficient $K_i$ to result by Formaggia et al. (2010) and d effective diffusion coefficient $D_{\mathrm {Eff},i}$ by Karner et al. (2001), Table 2 (Color figure online)

1.2 Appendix A.2 LDL-Related Parameters

The influx of native LDL through the endothelium described by the second Kedem–Katchalsky equation [cf. Eq. (4)] is well studied, and thus the required parameters are available in the literature. In contrast, the flux of modified LDL and native HDL is scant investigated. Due to its origin and equal size, it is convenient to use the same parameters for native and modified LDL. In contrast to native LDL, however, the concentration of modified LDL in blood is low (El-Bassiouni et al. 2007), and therefore we use $\eta _{{{\tilde{\ell }}}}=0$.

The weighting factors $\omega _{\ell }$, $\omega _{{{\tilde{\ell }}}}$ and $\omega _{h}$ for the average concentrations of native LDL, modified LDL and native HDL within the endothelium layer are estimated as proposed by Formaggia et al. (2010). The one-dimensional advection–diffusion equation is solved and volume-averaged over the domain of the endothelium. It follows that

$$\begin{aligned} \omega _i = \frac{\exp (Pe_i)}{\exp (Pe_i)-1}-\frac{1}{Pe_i}, \end{aligned}$$

(23)

where $Pe_i$ is the Péclet number of species i within the endothelium given by

$$\begin{aligned} Pe_i=\frac{\Vert {\varvec{u}} \Vert }{P_i}. \end{aligned}$$

(24)

Here, $\Vert {\varvec{u}} \Vert$ and $P_i$ are the transmural filtration velocity and the diffusive permeability of species i, respectively. Using $\Vert {{\varvec{u}} \Vert =6.41 \cdot 10^{-2} \; \frac{\mathrm {mm}}{\mathrm {h}}}$ (Formaggia et al. 2010; Yang and Vafai 2006; Meyer and Tedgui 1996) and $P_{\ell }= P_{{{\tilde{\ell }}}}= 6.12 \cdot 10^{-5} \; \frac{\mathrm {mm}}{\mathrm {h}}$ (Tompkins 1991; Yang and Vafai 2006) results in $Pe_{\ell }=Pe_{{{\tilde{\ell }}}}= 1.05 \cdot 10^{3}$ and weighting factors $\omega _{\ell }=\omega _{{{\tilde{\ell }}}}=9.99 \cdot 10^{-1}$.

To estimate the initial rate of recruitment of macrophages $r_{m}({{{\tilde{\ell }}}}_0,\Vert {\varvec{\tau }} \Vert )$, we use an initial concentration of modified LDL ${{{\tilde{\ell }}}}_0=7.2 \cdot 10^{-4} \; \eta _{\ell }$ based on the experimental results in Herrmann et al. (1994) and Tompkins (1991).

1.3 Appendix A.3 HDL-Related Parameters

HDL is a smaller particle than LDL. More precisely, LDL and HDL have radii of ${R_{\ell }=11.0 \; \mathrm {nm}}$ (Karner et al. 2001) and ${R_{h}=4.72 \; \mathrm {nm}}$ (Kontush and Chapman 2006), respectively. As a consequence, HDL has approximately an 1.87 times higher diffusive permeability compared to LDL, i.e., $P_{h}=1.87 \; P_{\ell }=1.14 \cdot 10^{-4} \; \frac{\mathrm {mm}}{\mathrm {h}}$ (Stender and Zilversmit 1981; Tompkins 1991). Together with Eqs. (23) and (24), it follows the weighting factor $\omega _{h}=9.98 \cdot 10^{-1}$ for the average concentrations of native HDL in the endothelium layer.

Karner et al. (2001) investigated the transport rates of ADP, albumin and LDL through the endothelium and the internal elastic lamina. As ADP and albumin have a smaller and LDL has a larger radius compared to HDL, their filtration reflection coefficients are used to estimate the filtration reflection coefficient $\sigma _{\mathrm {F},{h}}$ of HDL. We performed a least-squares fit of the filtration reflection coefficient as given in Karner et al. (2001), Table 3 to a saturating function in the particle radius $R_i$ of the form $\sigma _{\mathrm {F},i}(R_i) = \frac{R_i^a}{b^a+R_i^a}$. The least-squares fit yields $a=3.006$ and $b=2.112 \; \mathrm {nm}$ and so

$$\begin{aligned} \sigma _{\mathrm {F},i}(R_i) = \frac{R_i^{3.006}}{{(2.112\; \mathrm {nm})}^{3.006}+R_i^{3.006}}, \end{aligned}$$

(25)

which is visualized in Fig. 10b. The filtration reflection coefficient scales approximately with the volume of particles, and for HDL this gives ${\sigma _{\mathrm {F},{h}}=9.18 \cdot 10^{-1}}$.

The hindrance coefficient of LDL in the media is given by ${K_{{\ell }}=K_{{{{\tilde{\ell }}}}}=0.117}$ (Formaggia et al. 2010; Olgac et al. 2009), respectively. Assuming that the hindrance coefficient scales with the volume of particles (in consistent with the filtration reflection coefficient) and a saturating kinetic (in general it holds $0 \le K_i(R_i) \le 1$), it follows

$$\begin{aligned} K_i(R_i)=\frac{{(5.61 \; \mathrm {nm})}^3}{{(5.61\;\mathrm {nm})}^3+R_i^3}, \end{aligned}$$

(26)

which is plotted in Fig. 10c. Accordingly, the hindrance coefficient of HDL is estimated to $K_{h}=6.27 \cdot 10^{-1}$.

An additional unknown parameter is the effective diffusion coefficient of HDL $D_{\mathrm {Eff},h}$ within the artery wall. The effective diffusivity of LDL is measured as $D_{\mathrm {Eff},{\ell }}=D_{\mathrm {Eff},{{{\tilde{\ell }}}}}=1.26 \cdot 10^{-2} \; \frac{\mathrm {mm}^2}{\mathrm {h}}$ (Tomaso et al. 2011; Sun et al. 2007; Calvez et al. 2010), but no experimental results exist that allow quantifying the effective diffusivity of HDL. However, Karner et al. (2001) give the diffusivities of ADP, albumin and LDL in blood plasma. The data in Karner et al. (2001) are therefore normalized to the diffusivity of LDL in blood plasma and least-squares fitted to a rational function of the form $\frac{D_{\mathrm {Eff},i}(R_i)}{D_{\mathrm {Eff},{\ell }}}=\frac{e}{R_i^f}$. The least-squares fit yields $e=11.0 \; \mathrm {nm}$ and $f=1.0$ such that

$$\begin{aligned} D_{\mathrm {Eff},i}(R_i)=\frac{11.0\; \mathrm {nm}}{R_i} D_{\mathrm {Eff},{\ell }}, \end{aligned}$$

(27)

which is plotted in Fig. 10d. Here, the effective diffusion coefficients scales with the radius of particles and for HDL it yields $D_{\mathrm {Eff},{h}}=2.33 \; D_{\mathrm {Eff},{\ell }}=2.94 \cdot 10^{-2} \; \frac{\mathrm {mm}^2}{\mathrm {h}}$.

The rates of oxidative modification of HDL by macrophages $q_{{h},{m}}$ and endothelial cells $q_{{h},{e}}$ are crucial, but no experimental results exist that allow us to quantify them directly. Hence, the rates of HDL modification are calculated from the rates of LDL modification by considering the different structure and size of LDL and HDL. Therefore, we use

$$\begin{aligned} \begin{aligned} q_{{h},{m}}= \frac{q_{{\ell },{m}}}{7.6} \frac{N_{{{\tilde{\ell }}}}}{N_{{\tilde{h}}}}, \quad q_{{h},{e}}= \frac{q_{{\ell },{e}}}{7.6} \frac{N_{{{\tilde{\ell }}}}}{N_{{\tilde{h}}}}, \end{aligned} \end{aligned}$$

(28)

where $N_{{{\tilde{\ell }}}}$ and $N_{{\tilde{h}}}$ correspond to the amount of lipid peroxide in modified LDL and HDL, respectively. The factor 7.6 represents the relative difference between the surface areas of LDL and HDL (Cobbold et al. 2002). Using the values of $q_{{\ell },{m}}, q_{{\ell },{e}}, N_{{{\tilde{\ell }}}}$ and $N_{{\tilde{h}}}$ given in Thon et al. (2018), Table 4 yields $q_{{h},{m}}=1.64 \cdot 10^{-4} \; \frac{\mathrm {mm}^3}{\mathrm {h}}$ and $q_{{h},{e}}=6.21 \cdot 10^{-2} \; \frac{\mathrm {mm}}{\mathrm {h}}$.

1.4 Appendix A.4 Transmural flow

The Darcy permeability K must be estimated to fit to the murine physiology, i.e., to the murine intima–media thickness. The Darcy permeability is approximated by solving the norm of Eq. (9) for K:

$$\begin{aligned} K = \frac{\phi \mu \Vert {\varvec{u}} \Vert }{\Vert \nabla p_\mathrm {Med} \Vert }, \end{aligned}$$

(29)

where $\Vert {\varvec{u}} \Vert$ and $\Vert \nabla p_\mathrm {Med} \Vert$ correspond to the transmural filtration velocity and pressure gradient in the intima and media, respectively. The latter is approximated by the luminal blood pressure $\eta _p=100 \; \mathrm {mmHg}$ (Ai and Vafai 2006; Olgac et al. 2008; Whitesall et al. 2004), the pressure drop across the endothelium ${\varDelta p_\mathrm {End}=18 \; \mathrm {mmHg}}$ (Tedgui and Lever 1984) and the adventitial pressure ${p_\mathrm {Adv}=30 \; \mathrm {mmHg}}$ (Ai and Vafai 2006; Olgac et al. 2008; Yang and Vafai 2006) by: ${\Vert \nabla p_\mathrm {Med} \Vert = \frac{\eta _p - \varDelta p_\mathrm {End}-p_\mathrm {Adv}}{H}}=\frac{52 \; \mathrm {mmHg}}{0.04 \; \mathrm {mm}}$${=1.73 \cdot 10^{5} \; \frac{\mathrm {Pa}}{\mathrm {mm}}}$. Assuming a transmural filtration velocity ${\Vert {{\varvec{u}} \Vert =6.41 \cdot 10^{-2} \; \frac{\mathrm {mm}}{\mathrm {h}}}}$ (Formaggia et al. 2010; Yang and Vafai 2006; Meyer and Tedgui 1996), a porosity of $\phi =0.15$ (Ai and Vafai 2006; Prosi et al. 2005) and a dynamic viscosity of blood plasma of $\mu =2.0 \cdot 10^{-7} \;\mathrm {Pa}\; \mathrm {h}$ (Prosi et al. 2005; Yang and Vafai 2006) yield a Darcy permeability of ${K= 1.11 \cdot 10^{-14} \; \mathrm {mm}^2}$.

An overview of all parameters estimated and fitted so far is given in Table 2.

1.5 Appendix A.5 Wall Shear Stress-Dependent Parameters

There are experimental data by Sill et al. (1995) that quantify the hydraulic conductivity with respect to the WSS $\Vert {\varvec{\tau }} \Vert$. Sun et al. (2006) used these experimental results to parameterize the CSF (cf. Eq. (7)) which leads to: $\gamma _p=1.31 \cdot 10^{-1}$, $\mu _p=1.24 \cdot 10^{3} \; \frac{1}{\mathrm {Pa}}$ and $\xi _p=1.86 \cdot 10^{1}$. In Sun et al. (2006), the parameter $\mu _p$ was scaled so that it fits to a reference WSS value of $\Vert \overline{{\varvec{\tau }}}\Vert = 1.68 \; \mathrm {Pa}$. Even though the distribution of the reference WSS value $\Vert \overline{{\varvec{\tau }}}\Vert$ within an animal is more or less uniform (Sherman 1981), it varies significantly in between different animal models (Cheng et al. 2007). Therefore, the parameter $\mu _p$ of the CSF must be adapted to match the physiology of the animal under consideration, i.e., the murine physiology.

The same holds for the parameters $\xi _\tau$ and $\gamma _\tau$ of the macrophage recruitment submodel (cf. Eq. (3)) and the PSF (cf Eq. (6)). The estimated value $\xi _\tau =1.95 \cdot 10^{-1} \;\mathrm {Pa}$ corresponds to the human physiology with a reference WSS value $\Vert \overline{{\varvec{\tau }}}\Vert = 1.16 \; \mathrm {Pa}$ (Cheng et al. 2007). The parameter $\gamma _\tau$ is linked to a given reference WSS value $\Vert \overline{{\varvec{\tau }}}\Vert$ by $\gamma _\tau = \frac{1}{30} \Vert \overline{{\varvec{\tau }}}\Vert$, cf. Thon et al. (2018). A tabular overview of values for $\Vert \overline{{\varvec{\tau }}}\Vert$, $\xi _\tau$, $\gamma _\tau$ and $\mu _p$ for different animal models and the normalized case is given in Table 3.

1.6 Appendix A.6 Plaque-Specific Parameters

It remains to specify the concentrations of native LDL $\eta _{\ell }$ and HDL $\eta _{h}$ in blood and the WSS $\Vert {\varvec{\tau }} \Vert$ that the model plaque is exposed to in vivo. These parameters characterize the physiology and diet of the plaque’s host and the position of the plaque in the cardiovascular system. Thus, they cannot be set at fixed values, but their full ranges must be considered. The WSS $\Vert {\varvec{\tau }} \Vert$ within a murine aortic arch is below approximately $7.7 \Vert \overline{{\varvec{\tau }}}\Vert$ (Thon et al. 2018). In a clinical context, the concentrations of LDL and HDL are measured by determining their cholesterol contents in blood. In humans, the physiological ranges lie approximately in between concentrations of $50 {-} 250 \; \frac{\mathrm {mg}}{\mathrm {dl}}$ of LDL blood cholesterol and $20 {-} 80 \; \frac{\mathrm {mg}}{\mathrm {dl}}$ of HDL blood cholesterol (National Institutes of Health and National Heart, Lung and Blood Institute 2001), which can be transformed into SI units of particles per volume using $\rho _{8}=4.36 \cdot 10^{17} \; \frac{1}{\mathrm {g}}$ and $\rho _{13}=7.34 \cdot 10^{18} \; \frac{1}{\mathrm {g}}$ (see Thon et al. 2018, Table 1), respectively. In the case of mice with genetic modifications and high-fat diets, the LDL and HDL cholesterol concentrations can rise above $3000 \; \frac{\mathrm {mg}}{\mathrm {dl}}$ and $400 \; \frac{\mathrm {mg}}{\mathrm {dl}}$, respectively (Véniant et al. 2001; Lee et al. 2017). In general, however, mice show lower total blood cholesterol concentrations compared to humans, and in mice, as opposed to humans, HDL cholesterol is the predominant lipoprotein (Lee et al. 2017). An overview of the full spectrum of LDL and HDL blood cholesterol concentrations as well as WSS is given in Table 4.

Appendix B Non-spatial Model

A non-spatial version of the spatially resolved model developed in Sect. 2.2 is first given in this section. It is important to note that the non-spatial model is equivalent to the spatially resolved model, where the concentrations are homogeneous, e.g., induced by high effective diffusion coefficients $D_{\mathrm {Eff},i}\rightarrow \infty$ ($i={\ell },\ldots ,m$). Subsequently, the non-spatial model is used to effectively perform sensitivity and stability analyses.

1.1 Appendix B.1 Model Overview and Proposition 1

The non-spatial model of early atherosclerosis consists of the parameterized ODE model developed in Thon et al. (2018) enriched by the submodels of macrophage recruitment and lipoprotein fluxes in Sects. 2.1.2 and 2.1.3 . Altogether, the non-spatial model reads

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\ell }(t) =&- \mu _{{\ell }} \frac{{\ell }^{n_{{\ell }}}}{{(\xi _{{\ell }})}^{n_{{\ell }}} + {{\ell }}^{n_{{\ell }}}} m- \left( q_{{\ell },{m}} {\ell }m+ \frac{q_{{\ell },{e}}}{H} {\ell }\right) \cdot \frac{{(k_{h})}^{n_{h}}}{{(k_{h})}^{n_{h}}+{h}^{n_{h}}} + \frac{r_{\ell }({\ell }, \Vert {\varvec{\tau }} \Vert ) }{H}, \nonumber \\ \frac{\mathrm {d}}{\mathrm {d}t}{{{\tilde{\ell }}}}(t) =&- \mu _{{{{\tilde{\ell }}}}} \frac{{{{{\tilde{\ell }}}}}^{n_{{{{\tilde{\ell }}}}}}}{{(\xi _{{{{\tilde{\ell }}}}})}^{n_{{{{\tilde{\ell }}}}}} + {{{{\tilde{\ell }}}}}^{n_{{{{\tilde{\ell }}}}}}} m+ \left( q_{{\ell },{m}} {\ell }m+ \frac{q_{{\ell },{e}}}{H} {\ell }\right) \cdot \frac{{(k_{h})}^{n_{h}}}{{(k_{h})}^{n_{h}}+{h}^{n_{h}}} + \frac{r_{{{\tilde{\ell }}}}({{{\tilde{\ell }}}}, \Vert {\varvec{\tau }} \Vert ) }{H}, \nonumber \\ \frac{\mathrm {d}}{\mathrm {d}t}h(t) =&-q_{{h},{m}} hm- \frac{q_{{h},{e}}}{H} h+\frac{r_{h}({h}, \Vert {\varvec{\tau }} \Vert ) }{H}, \nonumber \\ \frac{\mathrm {d}}{\mathrm {d}t}f(t) =&+ N_{f}\mu _{{\ell }} \frac{{\ell }^{n_{{\ell }}}}{{(\xi _{{\ell }})}^{n_{{\ell }}} + {\ell }^{n_{{\ell }}}} m+ N_{f}\mu _{{{{\tilde{\ell }}}}} \frac{{{{{\tilde{\ell }}}}}^{n_{{{{\tilde{\ell }}}}}}}{{(\xi _{{{{\tilde{\ell }}}}})}^{n_{{{{\tilde{\ell }}}}}} + {{{{\tilde{\ell }}}}}^{n_{{{{\tilde{\ell }}}}}}} m-k_{f}{ \frac{{\left( {f}-f_\mathrm {Min}{m}\right) }^2}{f_\mathrm {Max}{m}-{f}} } \nonumber \\&+ k_{b}{b} - \mu _{f}\frac{{h}^{n_{f}}}{{(\xi _{f})}^{n_{f}}+{h}^{n_{f}}} {\left( {f}-f_\mathrm {Min}{m}\right) } +\frac{r_{m}\left( {{{\tilde{\ell }}}},\Vert {\varvec{\tau }} \Vert \right) }{H} f_\mathrm {In}, \nonumber \\ \frac{\mathrm {d}}{\mathrm {d}t}b(t) =&+k_{f}{ \frac{{\left( {f}-f_\mathrm {Min}{m}\right) }^2}{f_\mathrm {Max}{m}-{f}} } - k_{b}{b}, \nonumber \\ \frac{\mathrm {d}}{\mathrm {d}t}m(t) =&- \mu _{m}\frac{f^{n_{m}}}{{(\xi _{m}m)}^{n_{m}}+f^{n_{m}}} m+\frac{r_{m}\left( {{{\tilde{\ell }}}},\Vert {\varvec{\tau }} \Vert \right) }{H} , \end{aligned}$$

(30)

where the originally fixed-valued parameters corresponding to the fluxes of native LDL $r_{\ell }$, modified LDL $r_{{{\tilde{\ell }}}}$ and native HDL $r_{h}$ as well as the recruitment of macrophages $r_{m}$ were already notated including their explicit dependencies given by the submodels:

$$\begin{aligned} \begin{aligned} r_{\ell }\left( {\ell }, \Vert {\varvec{\tau }} \Vert \right)&= P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) \left( \eta _{\ell }- {\ell }\right) \\&\quad +(1-\sigma _{\mathrm {F},{\ell }} ) \left( \omega _{\ell }\eta _{\ell }+ (1- \omega _{\ell }) {\ell }\right) J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ), \\ r_{{{\tilde{\ell }}}}({{{\tilde{\ell }}}}, \Vert {\varvec{\tau }} \Vert )&= - P_{{{\tilde{\ell }}}}s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) {{{\tilde{\ell }}}}+ (1-\sigma _{\mathrm {F},{{{\tilde{\ell }}}}} ) (1- \omega _{{{\tilde{\ell }}}}) {{{\tilde{\ell }}}}J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ), \\ r_{h}\left( {h}, \Vert {\varvec{\tau }} \Vert \right)&= P_{h}s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) \left( \eta _{h}- h\right) \\&\quad + (1-\sigma _{\mathrm {F},{h}} )\left( \omega _{h}\eta _{h}+ (1- \omega _{h}) h\right) J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ), \\ r_{m}({{{\tilde{\ell }}}},\Vert {\varvec{\tau }} \Vert )&= P_{m}\left( 1- \delta _{m}\frac{k_{m}}{k_{m}+{{{\tilde{\ell }}}}} \right) \frac{ {(\xi _\tau )}^{\nu _\tau }}{{(\xi _\tau )}^{\nu _\tau }+{\Vert {\varvec{\tau }} \Vert }^{\nu _\tau }}, \\ J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert )&= L_p s_\mathrm {L}(\Vert {\varvec{\tau }} \Vert ) \left( \eta _p - p \right) , \\ s_\mathrm {P} \left( \Vert {\varvec{\tau }} \Vert \right)&= \frac{1}{\ln (2)} \ln \left( 1 + \zeta _\tau \frac{\gamma _\tau }{\Vert {\varvec{\tau }} \Vert + \gamma _\tau }\right) , \\ s_\mathrm {L}(\Vert {\varvec{\tau }} \Vert )&= \gamma _p \ln \left( \mu _p \Vert {\varvec{\tau }} \Vert + \xi _p \right) . \end{aligned} \end{aligned}$$

(31)

The initial conditions of the non-spatial model read analog to Thon et al. (2018)

$$\begin{aligned} \begin{aligned} {\ell }(0)&= 0 ,\quad {{{\tilde{\ell }}}}(0)= {{{\tilde{\ell }}}}_0 ,\quad h(0)= 0 ,\quad f(0)= f_0 m_0 , \\ b(0)&= b_0 m_0 ,\quad m(0)= m_0, \end{aligned} \end{aligned}$$

(32)

where $m_0$ is adapted due to the employed submodel of macrophage recruitment:

$$\begin{aligned} \begin{aligned} m_0&= \frac{r_{m}\left( {{{\tilde{\ell }}}}_0,\Vert {\varvec{\tau }} \Vert \right) }{H} \frac{{(\xi _{m})}^{n_{m}}+{(f_0)}^{n_{m}}}{\mu _{m}{(f_0)}^{n_{m}}}, \\ b_0&= \frac{k_{f}}{k_{b}} \frac{{\left( {f_0}-f_\mathrm {Min}\right) }^2}{f_\mathrm {Max}-{f_0}}. \end{aligned} \end{aligned}$$

(33)

Proposition 1

Let ${\ell }(t),{{{\tilde{\ell }}}}(t),h(t),f(t),b(t),m(t) \ (t \ge 0)$ be the unique and smooth solution of the initial value problem defined by Eqs. (30)–(33) with strictly positive parameters fulfilling $(1-\sigma _{\mathrm {F},i})(1-\omega _i)J_\mathrm {Vol}(p,\Vert {\varvec{\tau }} \Vert ) \le P_i s_\mathrm {P}(\Vert {\varvec{\tau }} \Vert )$, $0 \le \omega _i \le 1$, ${0 \le \sigma _{\mathrm {F},i} \le 1} \ ({i={\ell },{{{\tilde{\ell }}}},h})$, $0 \le p \le \eta _p$, $f_\mathrm {Min} \le f_\mathrm {In} < f_\mathrm {Max}$ and $f_\mathrm {Min} \le f_0 < f_\mathrm {Max}$. Then, the solution satisfies:

• 1. ${\ell }(t), {{{\tilde{\ell }}}}(t), h(t), f(t), b(t), m(t) \ge 0$ for all $t \ge 0$.

• 2.
  

  $\frac{f(t)}{m(t)} \in \left[ f_\mathrm {Min} , f_\mathrm {Max} \right]$ for all $t \ge 0$.

• 3. ${\ell }(t), {{{\tilde{\ell }}}}(t), h(t), f(t), m(t)$ are bounded.

Proof

The proof of Proposition 1 is similar to the proof of the proposition given in Thon et al. (2018). First, it follows from $\eta _p \ge p$ that

$$\begin{aligned} J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ) \overset{(31)}{=} L_p s_\mathrm {L}(\Vert {\varvec{\tau }} \Vert ) \left( \eta _p - p \right) \ge 0. \end{aligned}$$

(34)

To prove the positivity of ${\ell }$, i.e., ${\ell }(t)\ge 0 \; \forall t\ge 0$, it is sufficient to note that ${\ell }(0)=0$ and that ${\ell }(t)=0$ implies

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\ell }(t) \overset{(30)}{=} \frac{P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) \eta _{\ell }+ (1-\sigma _{\mathrm {F},{\ell }} ) \omega _{\ell }\eta _{\ell }J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert )}{H} \overset{(34),1\ge \sigma _{\mathrm {F},{\ell }}}{>} 0, \end{aligned}$$

(35)

due to the strict positivity of the parameters. The positivities of $h, m$ and ${{{\tilde{\ell }}}}$ are proved in an analog fashion. Since $\frac{f(0)}{m(0)}=f_0 \ge f_\mathrm {Min}$ and $\frac{f(t)}{m(t)}=f_\mathrm {Min}$ implies

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( \frac{f(t)}{m(t)}\right)&= \frac{\frac{\mathrm {d}}{\mathrm {d}t}f(t) -\frac{f(t)}{m(t)}\frac{\mathrm {d}}{\mathrm {d}t}m(t)}{m(t)} \\&\overset{(30)}{\ge } \frac{\frac{r_{m}({{{\tilde{\ell }}}}(t),\Vert {\varvec{\tau }}\Vert )}{H} f_\mathrm {In} -f_\mathrm {Min}\frac{r_{m}({{{\tilde{\ell }}}}(t),\Vert {\varvec{\tau }}\Vert )}{H}}{m(t)} {\ge } 0, \end{aligned} \end{aligned}$$

(36)

it holds $\frac{f(t)}{m(t)} \ge f_\mathrm {Min} \; \forall t \ge 0$. This also implies the positivity of $f$. Given that $\frac{f(0)}{m(0)}=f_0 < f_\mathrm {Max}$ and that $\frac{f(t)}{m(t)}\rightarrow f_\mathrm {Max}$ implies

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( \frac{f(t)}{m(t)}\right) = \frac{\frac{\mathrm {d}}{\mathrm {d}t}f(t) -\frac{f(t)}{m(t)}\frac{\mathrm {d}}{\mathrm {d}t}m(t)}{m(t)} {\longrightarrow } -\infty , \end{aligned}$$

(37)

it follows $\frac{f(t)}{m(t)} \le f_\mathrm {Max} \; \forall t \ge 0$. Hence, it is concluded that

$$\begin{aligned} \frac{f(t)}{m(t)} \in \left[ f_\mathrm {Min} , f_\mathrm {Max} \right] \; \forall t \ge 0. \end{aligned}$$

(38)

The positivity of $b$ follows since $b(0)=0$ and $b(t)=0$ implies

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}b(t) \overset{(30)}{=} k_{f}{ \frac{{\left( {f(t)}-f_\mathrm {Min}{m}\right) }^2}{f_\mathrm {Max}{m}-{f(t)}} } \overset{(38)}{\ge } 0 \end{aligned}$$

(39)

which finishes the proof of 1. (It also follows that the time-dependent solution $({\ell }(t),{{{\tilde{\ell }}}}(t),h(t),$$f(t),b(t),m(t)), t\ge 0$ of the initial value problem is unique and smooth because the smoothness of the right-hand side of the ODE (30) is now straightforward to show.)

Using (38)

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}m(t)&\overset{(30),(38)}{\ge } - \underbrace{\mu _{m}\frac{{(f_\mathrm {Max})}^{n_{m}}}{{(\xi _{m})}^{n_{m}}+{(f_\mathrm {Max})}^{n_{m}}}}_{=:z_\mathrm {Max}} m+\frac{r_{m}({{{\tilde{\ell }}}}(t),\Vert {\varvec{\tau }}\Vert )}{H}\\&\overset{(31)}{\ge } -z_\mathrm {Max} m+\frac{r_{m}(0,\Vert {\varvec{\tau }}\Vert )}{H} \end{aligned} \end{aligned}$$

(40)

holds, and by solving this ordinary differential inequality with associated initial condition ${m(0)=m_0}$ it follows

$$\begin{aligned} \begin{aligned} m(t)&\overset{(40)}{\ge } m_0\exp \left( - z_\mathrm {Max} t \right) + \frac{r_{m}(0,\Vert {\varvec{\tau }}\Vert )}{H z_\mathrm {Max}} \left( 1 - \exp \left( - z_\mathrm {Max} t \right) \right) \\&\ge \min \left( m_0 , \frac{r_{m}(0,\Vert {\varvec{\tau }}\Vert )}{H z_\mathrm {Max}} \right) \overset{(33),f_\mathrm {Max}> f_0}{=} \frac{r_{m}(0,\Vert {\varvec{\tau }}\Vert )}{H z_\mathrm {Max}} \\&= \frac{r_{m}(0,\Vert {\varvec{\tau }} \Vert )}{H} \frac{{(\xi _{m})}^{n_{m}}+{(f_\mathrm {Max})}^{n_{m}}}{\mu _{m}{(f_\mathrm {Max})}^{n_{m}}} \; \forall t \ge 0. \end{aligned} \end{aligned}$$

(41)

In an analog manner, the upper bound for $m(t)$ is found, leading to

$$\begin{aligned} \begin{aligned} m(t)&\in \bigg [ \underbrace{\frac{r_{m}(0,\Vert {\varvec{\tau }} \Vert )}{H} \frac{{(\xi _{m})}^{n_{m}}+{(f_\mathrm {Max})}^{n_{m}}}{\mu _{m}{(f_\mathrm {Max})}^{n_{m}}}}_{=: m_\mathrm {Min}} \\&\quad , \underbrace{\frac{r_{m}(\infty ,\Vert {\varvec{\tau }} \Vert )}{H} \frac{{(\xi _{m})}^{n_{m}}+{(f_\mathrm {Min})}^{n_{m}}}{\mu _{m}{(f_\mathrm {Min})}^{n_{m}}}}_{=: m_\mathrm {Max}} \bigg ] \; \forall t\ge 0 \end{aligned} \end{aligned}$$

(42)

which finishes the proof of 2.

Due to $(1-\sigma _{\mathrm {F},{\ell }})(1-\omega _{\ell })J_\mathrm {Vol}(p,\Vert {\varvec{\tau }} \Vert ) \le P_{\ell }s_\mathrm {P}(\Vert {\varvec{\tau }} \Vert )$, the boundedness of ${\ell }(t)$ is given by

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\ell }(t)&\overset{(30),(42)}{\le } -\left( q_{{\ell },{m}} m_\mathrm {Min} + \frac{q_{{\ell },{e}}}{H} \right) {\ell }(t) + \frac{r_{\ell }\left( {\ell }, \Vert {\varvec{\tau }} \Vert \right) }{H} \nonumber \\ \overset{(31)}{=}&-\left( q_{{\ell },{m}} m_\mathrm {Min} + \frac{q_{{\ell },{e}}}{H} \right) {\ell }(t) + \left( P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) + (1-\sigma _{\mathrm {F},{\ell }} ) \omega _{\ell }J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ) \right) \frac{\eta _{\ell }}{H} \nonumber \\&+ \underbrace{\left( -P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) + (1-\sigma _{\mathrm {F},{\ell }} ) (1-\omega _{\ell }) J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ) \right) }_{\le 0} \frac{{\ell }(t)}{H} \nonumber \\ \le&-\left( q_{{\ell },{m}} m_\mathrm {Min} + \frac{q_{{\ell },{e}}}{H} \right) {\ell }(t) + \left( P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) + (1-\sigma _{\mathrm {F},{\ell }} ) \omega _{\ell }J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ) \right) \frac{\eta _{\ell }}{H} \end{aligned}$$

(43)

since the solution of the ordinary differential inequality (with associated initial condition ${\ell }(0)=0$) is bounded by

$$\begin{aligned} \begin{aligned} {\ell }(t) \overset{(43)}{\le }&\frac{\left( P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) + (1-\sigma _{\mathrm {F},{\ell }} ) \omega _{\ell }J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ) \right) \eta _{\ell }}{H q_{{\ell },{m}} m_\mathrm {Min} + q_{{\ell },{e}}}\\&\quad \left( 1 - \exp \left( - \left( q_{{\ell },{m}} m_\mathrm {Min} + \frac{q_{{\ell },{e}}}{H} \right) t \right) \right) \\ \le&\frac{\left( P_{\ell }s_\mathrm {P}\left( \Vert {\varvec{\tau }} \Vert \right) + (1-\sigma _{\mathrm {F},{\ell }} ) \omega _{\ell }J_\mathrm {Vol}(p,\Vert {\varvec{\tau }}\Vert ) \right) \eta _{\ell }}{H q_{{\ell },{m}} m_\mathrm {Min} + q_{{\ell },{e}}} < \infty . \end{aligned} \end{aligned}$$

(44)

In an analog manner, the boundedness of ${{{\tilde{\ell }}}}(t)$ and $h(t)$ are proved which finishes the proof of Proposition 1. $\square$

1.2 Appendix B.2 Sensitivity Analysis

The parameters estimated in Appendix A have a degree of uncertainty due to their origins, indifferent pieces of research used as experimental models, and measurement errors. To quantify the effect of uncertainties in the parameters on the computational results of the model, a local sensitivity analysis using the method of a metabolic control analysis (Zi 2011) is performed. However, the computational cost to do this analysis for the spatially resolved model is too large, so that a metabolic control analysis using the spatially resolved model is not achievable. Therefore, we use the non-spatial model from Appendix B.1 with prescribed subendothelial pressure $p=\eta _p-\varDelta p_\mathrm {End}= 82 \; \mathrm {mmHg}= 1.09 \cdot 10^4 \; \mathrm {Pa}$ (Tedgui and Lever 1984; Tomaso et al. 2011; Olgac et al. 2008; Cilla et al. 2014), LDL cholesterol concentration ${\eta _{\ell }=150 \; \frac{\mathrm {mg}}{\mathrm {dl}}}$, HDL cholesterol concentration $\eta _{h}=50 \; \frac{\mathrm {mg}}{\mathrm {dl}}$ and WSS $\Vert {\varvec{\tau }} \Vert = 10\% \Vert \overline{{\varvec{\tau }}}\Vert$.

The metabolic control analysis is performed in the same way as in Zi (2011) and Thon et al. (2018). Accordingly, we compare the normalized partial derivatives of all concentrations with respect to all non-spatial parameters p given in Table 2 at time $T=100 \; \text {weeks}$. The uncertainties of the remaining non-spatial parameters were previously addressed in Thon et al. (2018). As proposed in Zi (2011), the partial derivatives are estimated by using forward finite difference approximations with a sufficiently small variation parameter $\varepsilon =0.1\%$. Hence, the metabolic control coefficient $\mathrm {MCC}({\ell },p)$ of LDL ${\ell }$ with respect to a model parameter p is computed by

$$\begin{aligned} \mathrm {MCC}({\ell },p) = \frac{1}{{\ell }_p(T)} \frac{\partial }{\partial p} {\ell }_p (T) \approx \frac{1}{{\ell }_p(T)} \frac{{\ell }_{p+\varepsilon \%} (T) - {\ell }_p(T)}{\varepsilon }, \end{aligned}$$

(45)

where ${\ell }_{p+\varepsilon \%}$ denotes the concentration of native LDL ${\ell }$ computed with the parameter p perturbed by $\varepsilon$%. The metabolic control coefficients of all other species are computed in the same manner. The metabolic control coefficients of all species of the non-spatial model with respect to all non-spatial parameters from Table 2 are plotted in Fig. 11.

Fig. 11

Sensitivity analysis of the non-spatial model. Metabolic control coefficients of native LDL ${\ell }$, modified LDL ${{{\tilde{\ell }}}}$, HDL $h$, intracellular free cholesterol per macrophage $\frac{f}{m}$, intracellular cholesterol ester per macrophage $\frac{b}{m}$ and macrophages $m$ with respect to all non-spatial parameters p in Table 2. The values of the truncated bars are $\mathrm {MCC}({\ell },\sigma _{\mathrm {F},{\ell }})=-175.90$ and $\mathrm {MCC}({{{\tilde{\ell }}}},\sigma _{\mathrm {F},{\ell }})=-92.68$ (Color figure online)

From the sensitivity analysis, it follows that variations of the filtration reflection coefficients of LDL $\sigma _{\mathrm {F},{\ell }}$ and HDL $\sigma _{\mathrm {F},{h}}$ have the largest influence on the computational results. While the impact of the filtration reflection coefficient of HDL $\sigma _{\mathrm {F},{h}}$ is still moderate, the effect of slight deviation of $\sigma _{\mathrm {F},{\ell }}$ is severe. Even though the literature in general agrees on $\sigma _{\mathrm {F},{\ell }} \approx 9.97 \cdot 10^{-1}$  (Karner et al. 2001; Yang and Vafai 2006; Sun et al. 2007; Prosi et al. 2005; Ai and Vafai 2006), both parameters $\sigma _{\mathrm {F},{\ell }}$ and $\sigma _{\mathrm {F},{h}}$ require further attention, especially by experimental communities.

1.3 Appendix B.3 Stability Analysis

The outcome of the spatially resolved model is strongly dependent on blood cholesterol concentrations of LDL $\eta _{\ell }$ and HDL $\eta _{h}$ and the WSS $\Vert {\varvec{\tau }} \Vert$ which characterize the physiology and diet of the host and the position of the individual plaque within the cardiovascular system. They can—depending on the species of host, its predisposition and its diet—vary by several orders of magnitude (cf. Table 4) which results in qualitatively different predicted long-term outcomes. Due to the high computational cost of the spatially resolved model, a stability analysis is performed using the non-spatial model from Appendix B.1.

Proposition 1 from Appendix B.1 applies, as all its requirements are fulfilled by the non-spatial model with the complete parameter set from Tables 2 and 3 , and Thon et al. (2018), Table 4. Hence, the steady-state concentrations of macrophages ${{\widehat{{m}}}}$ and intracellular free cholesterol per macrophage $\frac{{{\widehat{f}}}}{{{\widehat{m}}}}$ satisfy

$$\begin{aligned} \begin{aligned} {{\widehat{m}}}&\in [ m_\mathrm {Min}, m_\mathrm {Max}] = [ 0.04 \cdot 10^{8}, 14.96 \cdot 10^{8} ] \; \frac{1}{\mathrm {mm}^3}, \\ \frac{{{\widehat{f}}}}{{{\widehat{m}}}}&\in [f_\mathrm {Min}, f_\mathrm {Max}] = \left[ 1.22 \cdot 10^{10}, 7.15 \cdot 10^{10} \right] \end{aligned} \end{aligned}$$

(46)

Fig. 12

Stability analysis of the non-spatial model. Boundedness of intracellular cholesterol ester (a–d), steady-state concentration of intracellular free cholesterol per macrophage $\displaystyle \frac{{{\widehat{f}}}}{{{\widehat{m}}}}$ (e–h), and steady-state density of macrophages ${{\widehat{m}}}$ (i–l) are predicted for varying LDL and HDL cholesterol concentrations $\eta _{\ell }$ and $\eta _{h}$ and various WSS $\Vert {\varvec{\tau }} \Vert$ (Color figure online)

and only the concentration of cholesterol ester b can be unbounded. The boundedness of intracellular cholesterol ester b, the steady-state concentration of intracellular free cholesterol per macrophages $\frac{{{\widehat{f}}}}{{{\widehat{m}}}}$ and the steady-state density of macrophages ${{\widehat{m}}}$ are computed in the crucial ranges of $\eta _{\ell }$, $\eta _{h}$ and $\Vert {\varvec{\tau }}\Vert$. High LDL cholesterol, low HDL cholesterol and low WSS promote atherosclerosis, and so the ranges that we use for the stability analysis are $\eta _{\ell }\in [10, 800 ] \; \frac{\mathrm {mg}}{\mathrm {dl}}$, $\eta _{h}\in [20 , 100 ] \; \frac{\mathrm {mg}}{\mathrm {dl}}$ and $\Vert {\varvec{\tau }} \Vert \in [5\% , 40\% ] \Vert \overline{{\varvec{\tau }}}\Vert$, cf. Table 4. The points where analysis is done are on an equidistant grid of the specified parameter space. The numerical results for varying blood cholesterol concentrations $\eta _{\ell }$ and $\eta _{h}$ and four different WSS levels $\Vert {\varvec{\tau }} \Vert$ are plotted in Fig. 12.