Lesion Dynamics Under Varying Paracrine PDGF Signaling in Brain Tissue

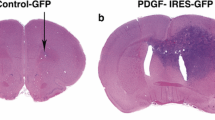
Abstract

Paracrine PDGF signaling is involved in many processes in the body, both normal and pathological, including embryonic development, angiogenesis, and wound healing as well as liver fibrosis, atherosclerosis, and cancers. We explored this seemingly dual (normal and pathological) role of PDGF mathematically by modeling the release of PDGF in brain tissue and then varying the dynamics of this release. Resulting simulations show that by varying the dynamics of a PDGF source, our model predicts three possible outcomes for PDGF-driven cellular recruitment and lesion growth: (1) localized, short duration of growth, (2) localized, chronic growth, and (3) widespread chronic growth. Further, our model predicts that the type of response is much more sensitive to the duration of PDGF exposure than the maximum level of that exposure. This suggests that extended duration of paracrine PDGF signal during otherwise normal processes could potentially lead to lesions having a phenotype consistent with pathologic conditions.

A Details of Derivation of \(p_0\)

Recall from Sect. 2.3 that we have the following relationship:

$$\begin{aligned} R(p_0+100)=4 R(p_0) \end{aligned}$$

(15)

which describes the increased activity of one condition of cells that has added exogenous PDGF relative to others that lack this added PDGF. Given that they are still active and have been injured during tissue removal, we assume that there is a shared baseline amount of PDGF, $p_0$.

Expanding this relationship using the definition of R(p) in (6), we have:

$$\begin{aligned}&R(p_0+100)=4 R(p_0) \end{aligned}$$

(16)

$$\begin{aligned}&\frac{\beta (p_0+100)}{\beta (EC_{50})+\beta (p_0+100)} = 4 \frac{\beta (p_0)}{\beta (EC_{50}) + \beta (p_0)} \end{aligned}$$

(17)

Since $\beta (EC_{50})$ is a constant, for notational simplicity, we set $\gamma =\beta (EC_{50})$ throughout the following algebra. This lets us write

$$\begin{aligned} \frac{\beta (p_0+100)}{\gamma +\beta (p_0+100)} = 4 \frac{\beta (p_0)}{\gamma + \beta (p_0)} \end{aligned}$$

(18)

Then, we can cross multiply the denominators and expand the $\beta$ terms:

$$\begin{aligned}&\beta (p_0+100) \left( \gamma +\beta (p_0)\right) = 4\beta (p_0)\left( \beta (p_0+100)+100 \right) \end{aligned}$$

(19)

$$\begin{aligned}&\frac{p_0+100}{k_m+p_0+100} \left( \gamma +\frac{p_0}{k_m+p_0}\right) = 4 \frac{p_0}{k_m+p_0} \left( \gamma + \frac{p_0+100}{k_m+p_0+100} \right) \end{aligned}$$

(20)

$$\begin{aligned}&\gamma \frac{p_0+100}{k_m+p_0+100}+\frac{p_0^2 + 100p_0}{\left( k_m+p_0+100\right) \left( k_m+p_0\right) } \nonumber \\&\qquad = 4 \gamma \frac{p_0}{k_m+p_0}+4 \frac{p_0^2+100p_0}{\left( k_m+p_0+100 \right) \left( k_m+p_0 \right) } \end{aligned}$$

(21)

Move all terms to one side for simplicity:

$$\begin{aligned} 4 \gamma \frac{p_0}{k_m+p_0} - \gamma \frac{p_0 100}{k_m+p_0+100} + 3 \frac{p_0^2 + 100p_0}{\left( k_m+p_0+100 \right) \left( k_m+p_0 \right) } = 0. \end{aligned}$$

(22)

Now, multiply both sides by $k_m + p_0$ and $k_m+p_0+100$:

$$\begin{aligned} 4 \gamma p_0\left( k_m+p_0+100 \right) - \gamma \left( p_0+100 \right) \left( k_m+p_0 \right) +3\left( p_0^2+100p_0 \right) =0. \end{aligned}$$

(23)

Expanding and then collecting by powers of $p_0$:

$$\begin{aligned}&4 \gamma p_0 k_m + 4 \gamma p_0^2 + 400 \gamma p_0 - \gamma k_m p_0 \nonumber \\&+ \gamma p_0^2 + 100 \gamma k_m + 100 \gamma p_0 + 3p_0^2 + 300p_0 = 0 \end{aligned}$$

(24)

$$\begin{aligned}&\left( 4 \gamma - \gamma + 3 \right) p_0^2 + \left( 4 \gamma k_m + 400 \gamma - \gamma k_m - 100 \gamma + 300 \right) p_0 - 100 \gamma k_m = 0 \end{aligned}$$

(25)

$$\begin{aligned}&\left( 3 \gamma + 3 \right) p_0^2 + \left( 3 \gamma k_m + 300 \gamma + 300 \right) p_0 - 100 \gamma k_m = 0. \end{aligned}$$

(26)

Now, we can use the quadratic formula to find the roots of this equation, letting

$$\begin{aligned} a&= 3 \gamma + 3 \end{aligned}$$

(27)

$$\begin{aligned} b&= 3 \gamma k_m + 300 \gamma + 300 \end{aligned}$$

(28)

$$\begin{aligned} c&= -100 \gamma k_m \end{aligned}$$

(29)

for the formula

$$\begin{aligned} p_0= \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. \end{aligned}$$

Recalling that we use parameter values $k_m = 30$ ng/mL and $EC_{50}=\sqrt{10}$, such that $\gamma = \frac{EC_{50}}{k_m + EC_{50}} = \frac{\sqrt{10}}{30+\sqrt{10}}$, this computes to (in decimal approximation):

$$\begin{aligned} p_0 \approx 0.8415, \quad -103.45 \end{aligned}$$

(30)

The latter of these does not make sense as a physical quantity, so we adopt the first as our approximate value for $p_0$:

$$\begin{aligned} p_0 = 0.8415 \text { ng/mL}. \end{aligned}$$

(31)