A Mathematical Model of Fluid Transport in an Accurate Reconstruction of Parotid Acinar Cells

Abstract

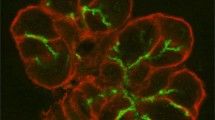
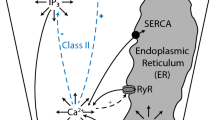
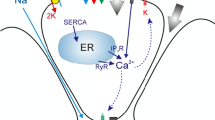
Salivary gland acinar cells use the calcium (${\mathrm{Ca}}^{2+}$) ion as a signalling messenger to regulate a diverse range of intracellular processes, including the secretion of primary saliva. Although the underlying mechanisms responsible for saliva secretion are reasonably well understood, the precise role played by spatially heterogeneous intracellular ${\mathrm{Ca}}^{2+}$ signalling in these cells remains uncertain. In this study, we use a mathematical model, based on new and unpublished experimental data from parotid acinar cells (measured in excised lobules of mouse parotid gland), to investigate how the structure of the cell and the spatio-temporal properties of ${\mathrm{Ca}}^{2+}$ signalling influence the production of primary saliva. We combine a new ${\mathrm{Ca}}^{2+}$ signalling model [described in detail in a companion paper: Pages et al. in Bull Math Biol 2018, submitted] with an existing secretion model (Vera-Sigüenza et al. in Bull Math Biol 80:255–282, 2018. https://doi.org/10.1007/s11538-017-0370-6) and solve the resultant model in an anatomically accurate three-dimensional cell. Our study yields three principal results. Firstly, we show that spatial heterogeneities of ${\mathrm{Ca}}^{2+}$ concentration in either the apical or basal regions of the cell have no significant effect on the rate of primary saliva secretion. Secondly, in agreement with previous work (Palk et al., in J Theor Biol 305:45–53, 2012. https://doi.org/10.1016/j.jtbi.2012.04.009) we show that the frequency of ${\mathrm{Ca}}^{2+}$ oscillation has no significant effect on the rate of primary saliva secretion, which is determined almost entirely by the mean (over time) of the apical and basal $[{\mathrm{Ca}}^{2+}]$. Thirdly, it is possible to model the rate of primary saliva secretion as a quasi-steady-state function of the cytosolic $[{\mathrm{Ca}}^{2+}]$ averaged over the entire cell when modelling the flow rate is the only interest, thus ignoring all the dynamic complexity not only of the fluid secretion mechanism but also of the intracellular heterogeneity of $[{\mathrm{Ca}}^{2+}]_i$. Taken together, our results demonstrate that an accurate multiscale model of primary saliva secretion from a single acinar cell can be constructed by ignoring the vast majority of the spatial and temporal complexity of the underlying mechanisms.

Appendices

Appendix

Fluxes of the Model

$$\begin{aligned} j_{\text {NaK}}&=\alpha _{\text {NaK}}\left( r \frac{[\text {K}^+]_e^2 [\text {Na}^+]_i^3}{[\text {K}^+]_e^2+\alpha [\text {Na}^+]_i^3} \right) , \end{aligned}$$

(18)

$$\begin{aligned} j_{\text {Nkcc1}}&=\alpha _{\text {Nkcc1}} \left( \frac{a_1-a_2 [\text {Na}^+]_i [\text {K}^+]_i [\text {Cl}^-]_i^2}{a_3+a_4 [\text {Na}^+]_i [\text {K}^+]_i [\text {Cl}^-]_i^2}\right) ,\end{aligned}$$

(19)

$$\begin{aligned} j_{\text {Nhe1}}&=G_{\text {Nhe1}} \Bigg (\frac{[\text {H}^+]_i}{[\text {H}^+]_i+K_\text {H}}\Bigg )^2 \Bigg (\frac{[{\mathrm{Na}}^+]_e}{[{\mathrm{Na}}^+]_e+K_{\text {Na}}} \Bigg ),\end{aligned}$$

(20)

$$\begin{aligned} J_{\text {Ae4}}&= G_{Ae4} \Bigg (\frac{[{\mathrm{Cl}}^-]_e}{[{\mathrm{Cl}}^-]_e + K_{\text {Cl}}}\Bigg ) \Bigg (\frac{[{\mathrm{Na}}^+]_i}{[{\mathrm{Na}}^+]_i+ K_{\text {Na}}}\Bigg ) \Bigg (\frac{[{\mathrm{HCO}}_3^-]_i}{[{\mathrm{HCO}}_3^-]_i+ K_{\text {B}}}\Bigg )^2,\end{aligned}$$

(21)

$$\begin{aligned} J_{\text {Buffer}}&=k_1[\text {CO}_2]_i-k_{-1}[\text {H}^+]_i[\text {HCO}_3^-]_i\end{aligned}$$

(22)

$$\begin{aligned} J^t_{{\mathrm{Na}}^+}&= \frac{G^t_{{\mathrm{Na}}^+}}{F z^{Na}} \Bigg [V_a - V_b - \frac{RT}{F} \ln \Bigg ( \frac{[{\mathrm{Na}}^+]_l}{[{\mathrm{Na}}^+]_e}\Bigg )\Bigg ],\end{aligned}$$

(23)

$$\begin{aligned} J^t_{{\mathrm{K}}^+}&= \frac{G^t_{{\mathrm{K}}^+}}{F z^{K}} \Bigg [V_a - V_b - \frac{RT}{F} \ln \Bigg ( \frac{[{\mathrm{K}}^+]_l}{[{\mathrm{K}}^+]_e}\Bigg )\Bigg ]. \end{aligned}$$

(24)

Water Fluxes

$$\begin{aligned} J^w_a&= P_a \Bigg ( \sum [c]_l + \varPsi _l - \sum [c]_i -\frac{x_i}{\omega _i}\Bigg ),\end{aligned}$$

(25)

$$\begin{aligned} J^w_b&= P_b \Bigg ( \sum [c]_i + \frac{x_i}{\omega _i} - \sum [c]_e \Bigg ),\end{aligned}$$

(26)

$$\begin{aligned} J^w_t&= P_t \Bigg ( \sum [c]_l + \varPsi _l - \sum [c]_e \Bigg ). \end{aligned}$$

(27)

Where,

$$\begin{aligned}&\sum [c]_e = [{\mathrm{K}}^+]_e + [{\mathrm{Na}}^+]_e + [{\mathrm{Cl}}^-]_e + [{\mathrm{HCO}}_3^-]_e + [\text {H}^+]_e + [\text {CO}_2]_e,\\&\sum [c]_i = [{\mathrm{K}}^+]_i+ [{\mathrm{Na}}^+]_i+ [{\mathrm{Cl}}^-]_i+ [{\mathrm{HCO}}_3^-]_i+ [\text {H}^+]_i + [{\mathrm{CO}}_2]_i,\\&\sum [c]_l = [{\mathrm{K}}^+]_l+ [{\mathrm{Na}}^+]_l+ [{\mathrm{Cl}}^-]_l+ [{\mathrm{HCO}}_3^-]_l + [\text {H}^+]_l. \end{aligned}$$

The parameter $x_i$ denotes the amount of negatively charged ions with valence $z = -1$impermeable to the cellular PM. Its value is determined by imposing electroneutrality in the cellular compartment. Note that all compartments of the model are assumed electroneutral at all times. The parameter $\varPsi _l$ in Eq. (26) represents the concentration of uncharged impermeable species present in the lumen, including (but not limited to) proteins such as amylase and big molecules like CO$_2$.

Parameters of the Model

See the Table 1.

Table 1 Table of parameters