Modeling Cell Dynamics in Colon and Intestinal Crypts: The Significance of Central Stem Cells in Tumorigenesis

Abstract

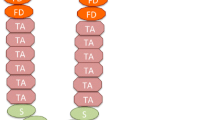
Colon and intestinal crypts have been widely chosen to study cell dynamics because of their fairly simple structures. In the colon and intestinal crypts, stem cells (SCs) are located at very bottom of the crypt, fully differentiated cells (FDs) are located in the top of the crypt, and transit-amplifying cells (TAs) are in the middle of the crypt between FDs and SCs. Recently, it has been discovered that there are two types of stem cells in the intestinal crypts: central stem cells (CeSCs) and border stem cells. To investigate dynamics of mutants in colon and intestinal crypts, we develop a four-compartmental stochastic model, which includes two SC compartments, and TAs and FDs compartments. We calculate the probability of the progeny of marked or mutant cells located at each of these compartments taking over the entire crypt or being washed out from the crypt. We found that the progeny of CeSCs will take over the entire crypt with a probability close to one. Interestingly, the progeny of advantageous mutant TAs and FDs will be washed out faster than disadvantageous mutants. Saliently, the model predicts that the time that the progeny of wild-type central stem cells will take over the mouse intestinal crypt is around 60 days, which is in perfect agreement with an experimental observation.

Appendices

Appendix

Materials and Methods

In this section, using the methods described in Shahriyari et al. (2016) and Wodarz and Komarova (2014), a generalized framework will be constructed to investigate cell dynamics in the colonic/intestinal crypt. In this model, we have a four-dimensional multivariable Markov model as the system of random movements over possible states $(e^{*}, b^{*}, d^{*}, f^{*})$ for $0\le e^{*}\le |S_c|,0\le b^{*}\le |S_b|, 0\le d^{*}\le |D_t|,$ and $0\le f^{*}\le |D_f|$. The total number of states is $(|S_c|+1)(|S_b|+1)(|D_t|+1)(|D_f|+1)$, where $|S_c|, \ |S_b|, \ |D_t|, \ |D_f|$ are the sizes of $S_c, \ S_b, \ D_t, \ D_f$ compartments, respectively.

We denote the probability of moving from the state a to the state b in one time step by $P_{a \rightarrow b}$, where $a,b\in \{(e^{*}, b^{*}, d^{*}, f^{*})\}$. For simplicity, indexes a and b only include the parameter(s), which are changing. For example, the probability $P_{e^{*} \rightarrow e^{*}+1}$ is the probability of moving from the state, which has $e^{*}$ number of $S_c$ mutants, to the state that has $e^{*}+1$ number of $S_c$ mutants in one time step, while the number of the other mutants (i.e., $b^{*}, d^{*}, f^{*}$) is not changed. All possible nonzero transition probabilities are listed below.

1.1 A. Transition Probabilities

• (1) $P_{{f}^{*}\rightarrow {f}^{*}+1} = \left( \frac{f}{f+ f^{*}} \right) ^{2} \left\{ 2\, \lambda _{f} \left( \frac{f}{\mathcal {F}} \right) \left( \frac{r_1\,f^{*}}{\mathcal {F}} \right) \right\} +$

  $\frac{2 f f^{*}}{(f+ f^{*})^2} \left\{ \lambda _f \left[ \frac{r_1\,f^{*}}{\mathcal{F}} \right] ^2 + (1-\lambda _f) \frac{r_1 d^{*}}{\mathcal{D}} \left[ (1-\lambda _s)\frac{r_1 d^{*}}{\mathcal{D}} + \lambda _s\,(1-\sigma )\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \ \right\} ,$

• (2) $P_{f^{*}\rightarrow f^{*}-1} = \frac{2 f f^{*}}{(f+ f^{*})^2} \,\left\{ \lambda _f \, \left( \frac{f}{\mathcal{F}} \right) ^2 + (1-\lambda _f)\,\frac{d}{\mathcal{D}} \left[ (1-\lambda _s)\, \frac{d}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{b}{\mathcal{R}_b} + \lambda _s\,\sigma \left( \delta \frac{b}{\mathcal{R}_b} \right. \right. \right.$

  $\left. \left. \left. + (1-\delta )(1-\gamma )\frac{b}{\mathcal{R}_b} \left( (1-\alpha ) + \alpha \, \frac{b}{b+b^{*}}\, \frac{e}{e+e^{*}} + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \right) + (1-\delta )\gamma \,\frac{e}{\mathcal{R}_c}\frac{e}{e+e^{*}}\right) \right] \right\}$

  $+ \left( \frac{f^{*}}{f+ f^{*}} \right) ^2 \left\{ 2\,\lambda _f \left( \frac{f}{\mathcal{F}} \right) \left( \frac{r_1 f^{*}}{\mathcal{F}} \right) \right\} ,$

• (3) $P_{f^{*}\rightarrow f^{*}+2}= \left( \frac{f}{f+ f^{*}} \right) ^2 \,\left\{ \lambda _f \, \left[ \frac{r_1\,f^{*}}{\mathcal{F}} \right] ^2 + (1-\lambda _f)\,\,\frac{r_1 d^{*}}{\mathcal{D}} \left[ (1-\lambda _s)\,\frac{r_1 d^{*}}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (4) $P_{f^{*}\rightarrow f^{*}-2}=\left( \frac{f^{*}}{f+ f^{*}} \right) ^2 \,\left\{ \lambda _f \, \left( \frac{f}{\mathcal{F}} \right) ^2 + (1-\lambda _f)\,\frac{d}{\mathcal{D}} \left[ (1-\lambda _s)\, \frac{d}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{b}{\mathcal{R}_b} + \lambda _s\,\sigma \left( \delta \frac{b}{\mathcal{R}_b} \right. \right. \right.$

  $\left. \left. \left. + (1-\delta )(1-\gamma )\frac{b}{\mathcal{R}_b} \left( (1-\alpha ) + \alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \right) + (1-\delta )\gamma \,\frac{e}{\mathcal{R}_c}\frac{e}{e+e^{*}}\right) \right] \right\} ,$

• (5) $P_{d^{*},f^{*}\rightarrow {d}^{*}-1,f^{*}+2}=\left( \frac{f}{f+ f^{*}} \right) ^{2}\,\left\{ (1-\lambda _{f})\,\frac{r_{1}\, {d}^{*}}{\mathcal {D}} \, \left[ (1-\lambda _s)\, \frac{d}{\mathcal {D}} + \lambda _s\,(1-\sigma )\,\frac{b}{\mathcal {R}_{b}} + \lambda _{s}\,\sigma \,\left( \delta \,\frac{b}{\mathcal {R}_{b}} \right. \right. \right.$

  $\left. \left. + \,(1-\delta )(1-\gamma )\frac{b}{\mathcal{R}_b} \left( (1-\alpha ) + \alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} + (1-\delta )\gamma \,\frac{e}{\mathcal{R}_c}\frac{e}{e+e^{*}} \right) \right] \right\} ,$

• (6) $P_{d^{*},{f}^{*}\rightarrow {d}^{*}-1,{f}^{*}+1} = \frac{2 f {f}^{*}}{(f+ {f}^{*})^{2}} \,\left\{ (1-\lambda _f)\,\frac{r_{1}\, {d}^{*}}{\mathcal {D}} \left[ (1-\lambda _s)\, \frac{d}{\mathcal {D}} + \lambda _{s}\,(1-\sigma )\,\frac{b}{\mathcal {R}_{b}} + \lambda _{s}\,\sigma \,\left( \delta \,\frac{b}{\mathcal {R}_b} \right. \right. \right.$

  $\left. \left. +\, (1-\delta )(1-\gamma )\frac{b}{\mathcal{R}_b} \left( (1-\alpha ) + \alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} + (1-\delta )\gamma \,\frac{e}{\mathcal{R}_c}\frac{e}{e+e^{*}} \right) \right] \right\} ,$

• (7) $P_{d^{*}\rightarrow d^{*}+1}= \left( \frac{f}{f + f^{*}} \right) ^2 \, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ (1-\lambda _s)\,\frac{r_1 d^{*}}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (8) $P_{d^{*},f^{*}\rightarrow d^{*}+1,f^{*}-1}= \frac{ 2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ (1-\lambda _s)\,\frac{r_1 d^{*}}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (9) $P_{d^{*},f^{*}\rightarrow d^{*}+1, f^{*}-2}= \left( \frac{f^{*}}{f + f^{*}} \right) ^2 \, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ (1-\lambda _s)\,\frac{r_1 d^{*}}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (10) $P_{b^{*},d^{*},f^{*}\rightarrow b^{*}-1,d^{*}+2, f^{*}-2} = \left( \frac{f^{*}}{f + f^{*}} \right) ^2 \, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,\delta \,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (11) $P_{b^{*},d^{*},f^{*}\rightarrow b^{*}-1,d^{*}+2, f^{*}-1}=\frac{ 2 f f^{*}}{(f+ f^{*})^2} \,\left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,\delta \,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (12) $P_{d^{*}\rightarrow {d}^{*}-1} = \left( \frac{f^{*}}{f+ {f}^{*}} \right) ^2 \, \left\{ (1-\lambda _{f})\,\frac{r_{1}\, {d}^{*}}{\mathcal {D}} \left[ (1-\lambda _{s})\, \frac{d}{{\mathcal {D}}} + \lambda _{s}\,(1-\sigma )\,\frac{b}{{\mathcal {R}}_{b}} + \lambda _{s}\,\sigma \,\left( \delta \,\frac{b}{{\mathcal {R}}_{b}}\right. \right. \right.$

  $\left. \left. + \,(1-\delta )(1-\gamma )\frac{b}{\mathcal{R}_b} \left( (1-\alpha ) + \alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} + (1-\delta )\gamma \,\frac{e}{\mathcal{R}_c}\frac{e}{e+e^{*}} \right) \right] \right\} ,$

• (13) $P_{b^{*},d^{*} \rightarrow b^{*}-1,d^{*}+2} = \left( \frac{f}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \delta \,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (14) $P_{b^{*},d^{*}, \rightarrow b^{*}+1,d^{*}-1} = \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{r_1 d^{*}}{\mathcal{D}} \left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \left( (1-\alpha ) \right. \right. \right. \right.$

  $\left. \left. \left. \left. +\alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}} +\alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} \right) + \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right) \right] \right\} ,$

• (15) $P_{b^{*},d^{*}\rightarrow b^{*}-1,d^{*}+1} = \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{r_1 d^{*}}{\mathcal{D}} \left[ \lambda _s\,\sigma \,\delta \,\frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (16) $P_{b^{*}\rightarrow b^{*}+1} = \left( \frac{f}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \left( (1-\alpha ) +\alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}} \right. \right. \right. \right.$

  $\left. \left. \left. \left. +\alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} \right) + \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right) \right] \right\} ,$

• (17) $P_{b^{*},f^{*}\rightarrow b^{*}+1,f^{*}-1} = \frac{2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \left( (1-\alpha ) \right. \right. \right. \right.$

  $\left. \left. \left. \left. +\,\alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}} +\alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} \right) + \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right) \right] \right\} ,$

• (18) $P_{b^{*},f^{*}\rightarrow b^{*}+1,f^{*}-2} = \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \left( (1-\alpha ) \right. \right. \right. \right.$

  $\left. \left. \left. \left. +\,\alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}} +\alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} \right) + \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right) \right] \right\} ,$

• (19) $P_{e^{*}\rightarrow e^{*}+1} = \left( \frac{f}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \, \alpha \, \frac{b^{*}}{b+b^{*}}+ \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c} \right) \,\frac{e}{e+e^{*}} \right] \right\} ,$

• (20) $P_{d^{**},f^{**}\rightarrow d^{**}-1,f^{**}+2}= \left( \frac{f}{f+ f^{*}} \right) ^2\,\left\{ (1-\lambda _f)\, \frac{r_2 d^{**}}{\mathcal{D}}\, \left[ (1-\lambda _s)\, \frac{d}{\mathcal{D}} + \lambda _s\,(1-\sigma )\,\frac{b}{\mathcal{R}_b} \right. \right.$

  $\,\,+ \,\lambda _s\,\sigma \,\left( \delta \,\frac{b}{\mathcal{R}_b} + (1-\delta )(1-\gamma )\frac{b}{\mathcal{R}_b} \left( (1-\alpha ) + \alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \right) \right.$

  $\left. \left. \left. + \,(1-\delta )\gamma \,\frac{e}{\mathcal{R}_c}\frac{e}{e+e^{*}} \right) \right] \right\} ,$

• (21) $P_{e^{*}, d^{*}\rightarrow e^{*}+1,d^{*}-1} = \left( \frac{f^{*}}{f+ f^{*}} \right) ^2 \!\! \left\{ (1-\lambda _f) \frac{r_1 d^{*}}{\mathcal{D}} \left[ \lambda _s\sigma (1-\delta ) \left( (1-\gamma ) \frac{r_1 b^{*}}{\mathcal{R}_b} \alpha \frac{b^{*}}{b+b^{*}}+ \gamma \frac{r_1 e^{*}}{\mathcal{R}_c} \right) \,\frac{e}{e+e^{*}} \right] \right\} ,$

• (22) $P_{e^{*},b^{*}\rightarrow e^{*}-1, b^{*}+1} = \left( \frac{f}{f+ f^{*}} \right) ^2\!\! \left\{ (1-\lambda _f)\, \frac{d}{\mathcal{D}}\! \left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{b}{\mathcal{R}_b}\,\alpha \, \frac{b}{b+b^{*}} + \gamma \,\frac{e}{\mathcal{R}_c} \! \right) \, \frac{e^{*}}{e + e^{*}} \! \right] \right\} ,$

• (23) $P_{e^{*},b^{*}, d^{*}\rightarrow e^{*}-1, b^{*}+1,d^{*}-1} = \left( \! \frac{f^{*}}{f+ f^{*}} \! \right) ^2\!\! \left\{ (1-\lambda _f) \frac{r_1 d^{*}}{\mathcal{D}} \! \left[ \lambda _s \sigma (1-\delta ) \! \left( (1-\gamma ) \frac{b}{\mathcal{R}_b} \alpha \frac{b}{b+b^{*}} + \gamma \,\frac{e}{\mathcal{R}_c} \right) \! \frac{e^{*}}{e + e^{*}} \! \right] \!\right\} ,$

• (24) $P_{b^{*},d^{*},f^{*}\rightarrow b^{*}-1,d^{*}+1,f^{*}+2}= \left( \! \frac{f}{f+ f^{*}} \! \right) ^2\, \left\{ (1-\lambda _f)\,\frac{r_1 d^{*}}{\mathcal{D}} \,\left[ \lambda _s\,\sigma \,\delta \, \frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (25) $P_{b^{*},d^{*},f^{*}\rightarrow b^{*}-1,d^{*}+1,f^{*}+1} = \frac{2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\,\frac{r_1 d^{*}}{\mathcal{D}} \,\left[ \lambda _s\,\sigma \,\delta \, \frac{r_1 b^{*}}{\mathcal{R}_b} \right] \right\} ,$

• (26) $P_{b^{*},d^{*}, f^{*}\rightarrow b^{*}+1,d^{*}-1, f^{*}+1} = \frac{2 f f^{*}}{(f+ f^{*})^2} \,\left\{ (1-\lambda _f)\,\frac{r_1 d^{*}}{\mathcal{D}} \left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \left( (1-\alpha ) \right. \right. \right. \right.$

  $\left. \left. \left. \left. +\,\alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}} +\alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} \right) + \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right) \right] \right\} ,$

• (27) $P_{b^{*},d^{*}, f^{*}\rightarrow b^{*}+1,d^{*}-1, f^{*}+2} = \left( \frac{f}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\,\frac{r_1 d^{*}}{\mathcal{D}} \left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \left( (1-\alpha ) \right. \right. \right. \right.$

  $\left. \left. \left. \left. +\,\alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}} +\alpha \, \frac{b}{b+b^{*}}\,\frac{e}{e+e^{*}} \right) + \gamma \,\frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right) \right] \right\} ,$

• (28) $P_{e^{*},b^{*},d^{*}, f^{*}\rightarrow e^{*}-1, b^{*}+1,d^{*}-1,f^{*}+1}$

  $=\frac{2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\, \frac{r_1 d^{*}}{\mathcal{D}} \left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{b}{\mathcal{R}_b}\,\alpha \, \frac{b}{b+b^{*}} + \gamma \,\frac{e}{\mathcal{R}_c} \right) \, \frac{e^{*}}{e + e^{*}} \right] \right\} ,$

• (29) $P_{e^{*},b^{*}, d^{*}, f^{*}\rightarrow e^{*}-1, b^{*}+1,d^{*}-1,f^{*}+2}$

  $=\left( \frac{f}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\, \frac{r_1 d^{*}}{\mathcal{D}}\left[ \lambda _s\,\sigma \,(1-\delta )\,\left( (1-\gamma )\,\frac{b}{\mathcal{R}_b}\,\alpha \, \frac{b}{b+b^{*}} + \gamma \,\frac{e}{\mathcal{R}_c} \right) \, \frac{e^{*}}{e + e^{*}} \right] \right\} ,$

• (30) $P_{e^{*},f^{*}\rightarrow e^{*}+1, f^{*}-1} \! = \! \frac{2 f f^{*}}{(f+ f^{*})^2} \! \left\{ (1-\lambda _f) \frac{d}{\mathcal{D}}\! \left[ \lambda _s\,\sigma \,(1-\delta )\! \left( (1-\gamma ) \frac{r_1\,b^{*}}{\mathcal{R}_b} \alpha \frac{b^{*}}{b+b^{*}} + \gamma \frac{r_1\,e^{*}}{\mathcal{R}_c} \right) \frac{e}{e + e^{*}} \right] \right\} ,$

• (31) $P_{e^{*},f^{*}\rightarrow e^{*}+1, f^{*}-2} \!=\! \left( \! \frac{f^{*} }{f+ f^{*}} \! \right) ^2\! \left\{ (1-\lambda _f)\, \frac{d}{\mathcal{D}}\! \left[ \! \lambda _s \sigma (1-\delta ) \left( (1-\gamma ) \frac{r_1\,b^{*}}{\mathcal{R}_b} \alpha \frac{b^{*}}{b+b^{*}} + \gamma \frac{r_1\,e^{*}}{\mathcal{R}_c} \right) \! \frac{e}{e + e^{*}} \! \right] \right\} ,$

• (32) $P_{e^{*},d^{*},f^{*}\rightarrow e^{*}+1,d^{*}-1, f^{*}+1}$

  $=\frac{2 f f^{*}}{(f+ f^{*})^2} \,\left\{ (1-\lambda _f)\, \frac{r_1\,d^{*}}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\, \left( (1-\gamma )\,\frac{r_1\,b^{*}}{\mathcal{R}_b}\,\alpha \, \frac{b^{*}}{b+b^{*}} + \gamma \,\frac{r_1\,e^{*}}{\mathcal{R}_c} \right) \, \frac{e}{e + e^{*}} \right] \right\} ,$

• (33) $P_{e^{*},d^{*},f^{*}\rightarrow e^{*}+1,d^{*}-1, f^{*}+2}$

  $=\left( \frac{f }{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\, \frac{r_1\,d^{*}}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\, \left( (1-\gamma )\,\frac{r_1\,b^{*}}{\mathcal{R}_b}\,\alpha \, \frac{b^{*}}{b+b^{*}} + \gamma \,\frac{r_1\,e^{*}}{\mathcal{R}_c} \right) \, \frac{e}{e + e^{*}} \right] \right\} ,$

• (34) $P_{e^{*},b^{*},f^{*}\rightarrow e^{*}-1,b^{*}+1,f^{*}-2} \!=\! \left( \! \frac{f^{*}}{f+ f^{*}} \!\! \right) ^2 \!\!\! \left\{ (1-\lambda _f) \frac{d}{\mathcal{D}} \! \!\left[ \! \lambda _s \sigma (1-\delta ) \! \left( (1-\gamma ) \frac{b}{\mathcal{R}_b} \alpha \frac{b}{b+b^{*}} \!+\! \gamma \frac{e}{\mathcal{R}_c} \right) \! \frac{e^{*}}{e + e^{*}} \! \right] \!\right\} ,$

• (35) $P_{e^{*},b^{*},f^{*}\rightarrow e^{*}-1,b^{*}+1,f^{*}-1} \! =\! \frac{2 f f^{*}}{(f+ f^{*})^2} \!\! \left\{ (1-\lambda _f) \frac{d}{\mathcal{D}}\!\! \left[ \lambda _s \sigma (1-\delta )\!\left( \! (1-\gamma )\frac{b}{\mathcal{R}_b} \alpha \frac{b}{b+b^{*}}+ \gamma \frac{e}{\mathcal{R}_c} \! \right) \! \frac{e^{*}}{e + e^{*}} \! \right] \! \right\} ,$

• (36) $P_{e^{*},b^{*}\rightarrow e^{*}+1, b^{*}-1} = \left( \frac{f}{f+ f^{*}} \right) ^2\,\left\{ (1-\lambda _f)\, \frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{b}{\mathcal{R}_b}\,\alpha \,\frac{b^{*}}{b+b^{*}}\, \frac{e}{e+e^{*}} \ \right] \right\} ,$

• (37) $P_{e^{*},b^{*},f^{*}\rightarrow e^{*}+1, b^{*}-1,f^{*}-1} = \frac{2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\, \frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{b}{\mathcal{R}_b}\,\alpha \,\frac{b^{*}}{b+b^{*}}\, \frac{e}{e+e^{*}} \ \right] \right\} ,$

• (38) $P_{e^{*},b^{*},f^{*}\rightarrow e^{*}+1, b^{*}-1,f^{*}-2} = \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\,\left\{ (1-\lambda _f)\, \frac{d}{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{b}{\mathcal{R}_b}\,\alpha \,\frac{b^{*}}{b+b^{*}}\, \frac{e}{e+e^{*}} \ \right] \right\} ,$

• (39) $P_{e^{*},b^{*},d^{*},f^{*}\rightarrow e^{*}+1, b^{*}-1,d^{*}-1,f^{*}+2}$

  $= \left( \frac{f}{f+ f^{*}} \right) ^2\,\left\{ (1-\lambda _f)\, \frac{r_1 d^{*}}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{b}{\mathcal{R}_b}\,\alpha \,\frac{b^{*}}{b+b^{*}}\, \frac{e}{e+e^{*}} \ \right] \right\} ,$

• (40) $P_{e^{*},b^{*},d^{*},f^{*}\rightarrow e^{*}+1, b^{*}-1,d^{*}-1,f^{*}+1}$

  $=\frac{2 f f^{*}}{(f+ f^{*})^2}\, \left\{ (1-\lambda _f)\, \frac{r_1 d^{*}}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{b}{\mathcal{R}_b}\,\alpha \,\frac{b^{*}}{b+b^{*}}\, \frac{e}{e+e^{*}} \ \right] \right\} ,$

• (41) $P_{e^{*},b^{*},d^{*}\rightarrow e^{*}+1, b^{*}-1,d^{*}-1} = \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\! \left\{ (1-\lambda _f)\, \frac{r_1 d^{*}}{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{b}{\mathcal{R}_b}\,\alpha \,\frac{b^{*}}{b+b^{*}}\, \frac{e}{e+e^{*}} \! \right] \right\} ,$

• (42) $P_{e^{*},b^{*}\rightarrow e^{*}-1, b^{*}+2} = \left( \frac{f}{f+ f^{*}} \right) ^2\,\left\{ (1-\lambda _f)\, \frac{d }{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\alpha \,\frac{b}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \! \right] \right\} ,$

• (43) $P_{e^{*},b^{*},f^{*}\rightarrow e^{*}-1, b^{*}+2,f^{*}-1} = \frac{2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\, \frac{d }{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\alpha \,\frac{b}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \ \right] \right\} ,$

• (44) $P_{e^{*},b^{*},f^{*}\rightarrow e^{*}-1, b^{*}+2,f^{*}-2} = \! \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\! \left\{ (1-\lambda _f)\, \frac{d }{\mathcal{D}}\, \left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\alpha \,\frac{b}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \! \right] \right\} ,$

• (45) $P_{e^{*},b^{*},d^{*},f^{*}\rightarrow e^{*}-1, b^{*}+2,d^{*}-1,f^{*}+2}$

  $= \left( \frac{f}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\, \frac{r_1 d^{*} }{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\alpha \,\frac{b}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \ \right] \right\} ,$

• (46) $P_{e^{*},b^{*},d^{*},f^{*}\rightarrow e^{*}-1, b^{*}+2,d^{*}-1,f^{*}+1}$

  $=\frac{2 f f^{*}}{(f+ f^{*})^2} \, \left\{ (1-\lambda _f)\, \frac{r_1 d^{*} }{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\alpha \,\frac{b}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \ \right] \right\} ,$

• (47) $P_{e^{*},b^{*},d^{*},f^{*}\rightarrow e^{*}-1, b^{*}+2,d^{*}-1,f^{*}+2}$

  $= \left( \frac{f^{*}}{f+ f^{*}} \right) ^2\, \left\{ (1-\lambda _f)\, \frac{r_1 d^{*} }{\mathcal{D}}\,\left[ \lambda _s\,\sigma \,(1-\delta )\,(1-\gamma ) \,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\alpha \,\frac{b}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \ \right] \right\} ,$

where $\mathcal{F}, \mathcal{D}, \mathcal{R}_b,\mathcal{R}_c$ are defined in the following

$$\begin{aligned} \mathcal{F} = r_1\,f^{*}+ f, \quad \mathcal{D} = r_1\,d^{*}+ d,\quad \mathcal{R}_b = r_1\,b^{*}+ b,\quad \mathcal{R}_c = r_1\,e^{*}+ e. \end{aligned}$$

1.2 B. Fixation Probability

In a one-dimensional Markov model when there is only one compartment X, the fixation probability $\pi ^{X}_j$, which is the probability that the progeny of j number of mutants will take over the entire compartment X of size $N>j$, satisfies the following system of the equations.

$$\begin{aligned} \left\{ \begin{array}{l} \pi ^X_j = \displaystyle \sum _{m} P_{j \rightarrow m} \pi ^X_m, \quad 1<j<N-1, \\ \pi ^X_1 = \displaystyle \sum _{m\ge 1} P_{1 \rightarrow m} \pi ^X_m, \\ \pi ^X_{N-1} = \displaystyle P_{N-1 \rightarrow N} + \sum _{m\le N-1} P_{j \rightarrow m} \pi ^X_m. \\ \pi ^X_N = 1, \end{array} \right. \end{aligned}$$

(1)

where $P_{j \rightarrow m}$ is the probability of transition from the state with j number of mutants to the state with m number of mutants in the population X.

1.3 C. The Fixation Probability of Stem Mutants Inside CeSC Group

To obtain the fixation probability of mutants in CeSCs, it is sufficient to trace mutants only in the stem cell niche, because only BSC mutants can migrate backward to $S_c$ and non-stem cell mutants cannot change the number of mutants in $S_c$. Hence, we denote the fixation probability of $e^{*}$ number of CeSCs and $b^{*}$ number of BSCs mutants in CeSCs by $\pi ^\mathrm{Ce}_{(e^{*},b^{*})}$. We consider a bi-variable Markov chain with the initial state $(e^{*},b^{*})=(1,0)$. Additionally, the initial conditions are $\pi ^\mathrm{Ce}_{(0,0)}=0$ and $\pi ^\mathrm{Ce}_{(S_c,b^{*})}=1$ for any $0\le b^{*} \le |S_b|$.

Here, we obtain the fixation probability $\pi ^\mathrm{Ce}_{(e^{*},b^{*})}$ through a two-variable Markov process of all possible states $(e^{*},b^{*})$ where $(e^{*},b^{*})\ne (0,0)$ and $0\le e^{*}\le |S_c|-1, 0\le b^{*}\le |S_b|$. The fixation probability $\pi ^\mathrm{Ce}_{(e^{*},b^{*})}$ satisfies the following system of equations, which is the two-dimensional version of the system of equations (1).

$$\begin{aligned} \pi ^\mathrm{Ce}_{(0,0)}= & {} 0 \nonumber \\ \pi ^{\mathrm{Ce}}_{(e^{*},b^{*})}= & {} \sum _{{\tilde{e^{*}},\tilde{b^{*}}}}\, P_{(e^{*},b^{*})\rightarrow (\tilde{e^{*}},\tilde{b^{*}})}\,\pi ^{\mathrm{Ce}}_{(\tilde{e^{*}},\tilde{b^{*}})}, \nonumber \\ \pi ^{\mathrm{Ce}}_{(|S_c|,b^{*})}= & {} 1, \quad \text {for all } 0\le b^{*}\le |S_b|. \end{aligned}$$

(2)

The above system of equations can be rewritten in the following matrix form.

$$\begin{aligned} \mathrm{P}^\mathrm{Ce}(e^{*},b^{*})\,\cdot \, \Pi ^\mathrm{Ce}(e^{*},b^{*}) = \mathrm{b}^\mathrm{Ce}, \end{aligned}$$

(3)

where

$$\begin{aligned} \Pi ^\mathrm{Ce}=\left( \begin{array}{c} \pi ^\mathrm{Ce}_{(1,0)} \\ \pi ^\mathrm{Ce}_{(2,0)} \\ \vdots \\ \pi ^\mathrm{Ce}(|S_c|-2,|S_b|) \\ \pi ^\mathrm{Ce}(|S_c|-1,|S_b|)\\ \end{array} \right) , \ \, b^\mathrm{Ce}=\mathbf{0}_{1\times |S_c|(|S_b|+1)}. \end{aligned}$$

(4)

The nonzero transition probabilities in $\mathrm{P}^{Ce}$ are

$$\begin{aligned} P_{(e^{*},b^{*})\rightarrow (e^{*}+1,b^{*})}= & {} \sigma (1-\delta )\, \left( (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b} \, \alpha \, \frac{b^{*}}{b+b^{*}} + \gamma \, \frac{r_1 e^{*}}{\mathcal{R}_c} \right) \,\frac{e}{e+e^{*}}, \nonumber \\ P_{(e^{*},b^{*})\rightarrow (e^{*},b^{*}+1)}= & {} \sigma (1-\delta )\, \left[ (1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b}\,\left( (1-\alpha ) + \alpha \, \frac{b^{*}}{b+b^{*}}\, \frac{e^{*}}{e+e^{*}} \right. \right. \nonumber \\&\quad \left. \left. +\, \alpha \, \frac{b}{b+b^{*}}\, \frac{e}{e+e^{*}} \right) + \gamma \, \frac{r_1 e^{*}}{\mathcal{R}_c}\,\frac{e^{*}}{e+e^{*}} \right] , \nonumber \\ P_{(e^{*},b^{*})\rightarrow (e^{*},b^{*}-1)}= & {} \sigma \delta \, \frac{r_1 b^{*}}{\mathcal{R}_b}, \nonumber \\ P_{(e^{*},b^{*})\rightarrow (e^{*}+1,b^{*}-1)}= & {} \sigma (1-\delta )\,(1-\gamma )\,\frac{b}{\mathcal{R}_b}\, \alpha \, \frac{b^{*}}{b+b^{*}}\,\frac{e}{e+e^{*}}, \nonumber \\ P_{(e^{*},b^{*})\rightarrow (e^{*}-1,b^{*}+1)}= & {} \sigma (1-\delta )\, \left[ (1-\gamma )\,\frac{b}{\mathcal{R}_b}\, \alpha \,\frac{b}{b+b^{*}} + \gamma \, \frac{e}{\mathcal{R}_c} \right] \,\frac{e^{*}}{e+e^{*}} , \nonumber \\ P_{(e^{*},b^{*})\rightarrow (e^{*}-1,b^{*}+2)}= & {} \sigma (1-\delta )\,(1-\gamma )\,\frac{r_1 b^{*}}{\mathcal{R}_b}\, \alpha \, \frac{b}{b+b^{*}}\,\frac{e^{*}}{e+e^{*}}. \end{aligned}$$

(5)

Here, we supposed that $\lambda _f<1, \lambda _s\ne 0, \sigma \ne 0$, and $0\le e^{*}\le |S_c|-1, 0\le b^{*}\le |S_b|$. We calculate the fixation probability $\pi ^\mathrm{Ce}_{(e^{*},b^{*})}$ of $e^{*}$ number of CeSC and $b^{*}$ number of BSC mutants in $S_c$, by numerically solving the system of Eq. 3.

Note that based on the transition probabilities, when stem cells divide only asymmetrically (i.e., when $\sigma =0$), then $\pi ^\mathrm{Ce}_{(e^{*},0)}=0$. Note, when stem cells divide asymmetrically, no division occurs in the CeSC compartment; thus, the number of CeSC mutants does not change. The same result can be obtained when division is only occurring in $D_t$ compartment ($\lambda _s=0$).

1.3.1 C1. The Fixation Probability of CeSC Mutants in $S_c$ for $\alpha =0$

When $\alpha =0$, $\lambda _s > 0$, and $\gamma >0$, we can simplify the system of Eq. (2) to the following system of equations for all $0\le b^{*}\le |S_b|$.

$$\begin{aligned}&r_1\,\pi ^\mathrm{Ce}_{(e^{*}+1,b^{*})} + \pi ^\mathrm{Ce}_{(e^{*}-1,b^{*})} - (1+r_1)\,\pi ^\mathrm{Ce}_{(e^{*},b^{*})}=0, \quad 1< e^{*} <S_c-1, \nonumber \\&r_1\,\pi ^\mathrm{Ce}_{(2,b^{*})} - (1+r_1)\,\pi ^\mathrm{Ce}_{(1,b^{*})}=0, \nonumber \\&r_1 + \pi ^\mathrm{Ce}_{(|S_c|-2,b^{*})} - (1+r_1)\, \pi ^\mathrm{Ce}_{(|S_c|-1,b^{*})}=0. \end{aligned}$$

(6)

From the above system of equations, we get

$$\begin{aligned} \pi ^\mathrm{Ce}_{(e^{*},b^{*})} = \frac{1-\left( \frac{1}{r_1} \right) ^{e^{*}}}{ 1-\left( \frac{1}{r_1} \right) ^{|S_c|} }, \quad \text { for all }\quad 1\le e^{*} \le |S_c|-1 \text { and } 0\le b^{*}\le |S_b| . \end{aligned}$$

(7)

Therefore, the fixation probability of one mutant central stem cell in $S_c$, i.e., the probability of the progeny of one CeSC mutant taking over the entire $S_c$, is

$$\begin{aligned} \pi ^\mathrm{Ce}_{(1,0)}= \frac{1-\left( \frac{1}{r_1} \right) }{ 1-\left( \frac{1}{r_1} \right) ^{|S_c|} }. \end{aligned}$$

(8)

1.4 D. The Fixation Probability of CeSC or BSC Mutants Inside $S_b$

Here, we obtain the fixation probability $\pi ^\mathrm{BC}_{(e^{*}, b^{*})}$, which is the probability that the progeny of $e^{*}$ number of CeSC and $b^{*}$ number of BSC mutants will take over $S_b$. Similar to the previous section, we consider a bi-variable Markov chain. Applying a two-variable Markov process of all possible states $(e^{*},b^{*})$ for $(e^{*},b^{*})\ne (0,0)$ and $0\le e^{*}\le |S_c|, 0\le b^{*}\le |S_b|-1$, the total number of different possible states is $(|S_c|+1)|S_b| -1$. The fixation probability $\pi ^\mathrm{BC}_{(e^{*}, b^{*})}$ satisfies the following system of equations

$$\begin{aligned} \pi ^\mathrm{BC}_{(0,0)}= & {} 0 \nonumber \\ \pi ^\mathrm{BC}_{(e^{*},b^{*})}= & {} \sum _{{\tilde{e^{*}},\tilde{b^{*}}}}\, P_{(e^{*},b^{*})\rightarrow (\tilde{e^{*}},\tilde{b^{*}})}\,\pi ^\mathrm{BC}_{(\tilde{e^{*}},\tilde{b^{*}})} \nonumber \\ \pi ^\mathrm{BC}_{(e^{*}, |S_b|)}= & {} 1 \quad \text { for all } 0\le e^{*}\le |S_c|. \end{aligned}$$

(9)

We calculate the fixation probability $\pi ^\mathrm{BC}_{(e^{*},b^{*})}$ of $e^{*}$ number of CeSC and $b^{*}$ number of BSC mutants in $S_b$, by numerically solving the matrix representation of the above system of equations (9). Note that when $\lambda _s=0$, $\lambda _f=1$, or $\sigma =0$, the number of BSC mutants does not change, therefore $\pi ^\mathrm{BC}_{(e^{*},b^{*})}=0$ for $b^{*}<|S_b|$.

1.4.1 D1. The Fixation Probability of BSC Mutants Inside $S_b$ for $\alpha =0$

Assuming $\lambda _s\ne 0, \lambda _f<1, \sigma \ne 0,$ and $\alpha =0$, the system (9) can be reduced to the following system for all $0\le e^{*} \le |S_c|$:

$$\begin{aligned} 0= & {} (1-\delta ) (1-\gamma )\,\pi ^\mathrm{BC}_{(e^{*},b^{*}+1)} + \delta \,\pi ^\mathrm{BC}_{(e^{*},b^{*}-1)} - ( (1-\delta ) (1-\gamma ) + \delta )\pi ^\mathrm{BC}_{(e^{*},b^{*})}, \nonumber \\ 0= & {} (1-\delta ) (1-\gamma ) \pi ^\mathrm{BC}_{(e^{*},2)} - ( (1-\delta ) (1-\gamma ) + \delta ) \pi ^\mathrm{BC}_{(e^{*},1)}, \nonumber \\ 0= & {} (1-\delta ) (1-\gamma )+ \delta \,\pi ^\mathrm{BC}_{(e^{*},|S_b|-2)} - ( (1-\delta ) (1-\gamma ) + \delta )\pi ^\mathrm{BC}_{(e^{*}, |S_b|-1)}. \end{aligned}$$

(10)

This system of equations reveals that

$$\begin{aligned} \pi ^\mathrm{BC}_{(e^{*},b^{*})} = \frac{1-\left( \frac{\delta }{(1-\delta )(1-\gamma )} \right) ^{b^{*}}}{ 1-\left( \frac{\delta }{(1-\delta )(1-\gamma )} \right) ^{|S_b|} }, \text { for all } 0\le e^{*} \le |S_c| \text { and } 1\le b^{*} \le |S_b|. \end{aligned}$$

(11)

Therefore, the fixation probability of a single BSC mutant in $S_b$ is given by

$$\begin{aligned} \pi ^\mathrm{BC}_{(e^{*},1)} = \frac{1-\left( \frac{\delta }{(1-\delta )(1-\gamma )} \right) }{ 1-\left( \frac{\delta }{(1-\delta )(1-\gamma )} \right) ^{|S_b|} }, \text { for all } 0\le e^{*} \le |S_c|. \end{aligned}$$

(12)

1.5 E. The Fixation Probability of TA Mutants Inside the TA Compartment

Here, we assume mutants are only located in the TA compartment, and all other cells in the other compartments are wild-type. Since TA mutants can only increase the number of mutants in FD and TA compartments and there is no backward migration from $D_f$ to $D_t$, only mutants in $D_t$ can change the number of mutants in the TA compartment. Thus, the fixation probability $\pi ^\mathrm{TA}_{d^{*}}$ of $d^{*}$ number of mutants in $D_t$ can be obtained using the following system of equations.

$$\begin{aligned} \mathrm{P}^\mathrm{TA}\,\cdot \, \Pi ^\mathrm{TA} = \mathrm{C}^\mathrm{TA}, \end{aligned}$$

(13)

where

$$\begin{aligned}&\mathrm{P}^\mathrm{TA} \!\!=\!\! \left( \!\! \begin{array}{c c c c c c c c } - \mathcal{A}(1) &{} P^{TA}_{1\rightarrow 2} &{} 0 &{} \cdots &{} 0&{} 0 &{} 0 \\ P^{TA}_{2\rightarrow 1} &{}- \mathcal{A}(2) &{} P^{TA}_{2\rightarrow 3} &{} \cdots &{} 0 &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} P^{TA}_{|D_t|-1\rightarrow |D_t|-2} &{}- \mathcal{A}(|D_t|-1) &{} P^{TA}_{|D_t|-1\rightarrow |D_t|} \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 1 \end{array} \!\!\right) , \end{aligned}$$

and

$$\begin{aligned} \Pi ^\mathrm{TA}=\left( \begin{array}{c } \pi ^\mathrm{TA}_1 \\ \pi ^\mathrm{TA}_2 \\ \vdots \\ \pi ^\mathrm{TA}_{|D_t|-1} \\ \pi ^\mathrm{TA}_{|D_t|} \end{array} \right) , \ \, \mathrm{C}^\mathrm{TA}=\left( \begin{array}{c } 0 \\ 0 \\ \vdots \\ 0 \\ 1\\ \end{array} \right) . \end{aligned}$$

(14)

$P^{TA}_{d^{*}\rightarrow d^{*}+1}$ is the sum of all the transition probabilities, which tend to an increase by one in the number of mutant TA cells, and $P^{TA}_{d^{*}\rightarrow d^{*}-1}$ is the sum over all the possible transition probabilities leading to a decrease by one in the number of mutant TA cells. More precisely,

$$\begin{aligned}&P^{TA}_{d^{*}\rightarrow d^{*}+1} = (1-\lambda _s)\, \frac{D_t - d^{*} }{ D_t +(r_1- 1)d^{*} } , \end{aligned}$$

(15)

$$\begin{aligned}&P^{TA}_{d^{*}\rightarrow d^{*}-1} = \lambda _s + \,(1-\lambda _s)\,\frac{D_t - d^{*} }{ D_t +(r_1- 1)d^{*} }, \\&\mathcal{A}(i) = \sum _{j\ne i} P^{TA}_{i \rightarrow j}, \quad \text{ for } 1\le i \le |D_t|.\nonumber \end{aligned}$$

(16)

The solution to this system is in the following form

$$\begin{aligned}&\quad \pi ^\mathrm{TA}_{d^{*}} = \displaystyle {\frac{ \sum _{k=0}^{d^{*}-1} \,\mathcal{H}(k)}{\sum _{k=0}^{|D_t|-1} \,\mathcal{H}(k)}}, \end{aligned}$$

(17)

$$\begin{aligned}&\quad \mathcal{H}(k) = \left( \frac{ \lambda _s \, r_1-1}{\lambda _s-1 } \right) ^k \frac{ \Gamma \left( \frac{ |D_t| + ( \lambda _s \, r_1 -1)(k+2) }{ \lambda _s\, r_1 -1} \right) \, \Gamma (2 - |D_t|) \,(1-\lambda _s) }{ \Gamma \left( \frac{ |D_t| + 2(\lambda _s\, r_1 -1) }{ \lambda _s\, r_1 -1} \right) \, \Gamma ( (k+1) - |D_t|) \,(1-\lambda _s\,r_1) }, \nonumber \\ \end{aligned}$$

(18)

where $\Gamma (t)=\int _0^{\infty } x^{t-1}\,\mathrm{e}^x\, \mathrm{d}x$ is the gamma function. Then, the fixation probability $\pi _1^\mathrm{TA}$ can be derived from the following relation

$$\begin{aligned} \pi ^\mathrm{TA}_1 = \mathcal{H}(0)\,\left[ \sum _{k=0}^{|D_t|-1} \,\mathcal{H}(k)\right] ^{-1}. \end{aligned}$$

(19)

Equation (13) implies that if $\lambda _s=0$, then $\pi ^\mathrm{TA}_{d^{*}}=\displaystyle {\frac{1}{|D_t|}}$.

1.6 F. The Fixation Probability of Mutant FD Cells in $D_f$

Assuming the initial state is $(e^{*}, b^{*}, d^{*},f^{*}) = (0,0, 0, f^{*} )$, only the number of FD mutants can vary. Therefore, the fixation probability of $f^{*}$ number of FD mutants, $\pi ^\mathrm{FD}_{f^{*}}$, can be obtained from the following system of equations.

$$\begin{aligned} \mathrm{P}^\mathrm{FD}\,\cdot \, \Pi ^\mathrm{FD} = \mathrm{C}^\mathrm{FD}, \end{aligned}$$

(20)

where

$$\begin{aligned}&\mathrm{P}^\mathrm{FD} \!\!=\!\! \\&\quad {\left( \!\! \begin{array}{c c c c c c c c c c c } - \mathcal{B}(1) &{} P^{FD}_{1\rightarrow 2} &{} P^{FD}_{1\rightarrow 3} &{} 0 &{} 0 &{} \cdots &{} 0&{} 0 &{} 0 &{}0 &{} 0 \\ P^{FD}_{2\rightarrow 1} &{}- \mathcal{B}(2) &{} P^{FD}_{2\rightarrow 3} &{} P^{FD}_{2\rightarrow 4} &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} 0&{} \cdots &{}0 &{} P^{FD}_{_{|D_f|-1 \rightarrow |D_f|-3}} &{} P^{FD}_{_{|D_f|-1 \rightarrow |D_f|-2}} &{}- \mathcal{B}(|D_f|-1) &{} P^{FD}_{_{|D_f|-1 \rightarrow |D_f|}} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array} \!\!\right) ,} \end{aligned}$$

and

$$\begin{aligned} \Pi ^\mathrm{FD}=\left( \begin{array}{c } \pi ^\mathrm{FD}_{1} \\ \pi ^\mathrm{FD}_{2} \\ \vdots \\ \pi ^\mathrm{FD}_{|D_f|-1} \\ \pi ^\mathrm{FD}_{|D_f|} \end{array} \right) , \ \, \mathrm{C}^{f^{*}}=\left( \begin{array}{c } 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{array} \right) , \end{aligned}$$

(21)

where

$$\begin{aligned}&P^{FD}_{f^{*} \rightarrow f^{*}+2} = \lambda _f\,\left( \frac{r_1\,f^{*}}{|D_f|+(r_1-1)f^{*}}\right) ^2,\\&P^{FD}_{f^{*} \rightarrow f^{*}+1} = 2\,\lambda _f\, \frac{r_1\,f^{*}}{ |D_f|+(r_1-1)f^{*}},\\&P^{FD}_{f^{*} \rightarrow f^{*}-1} = 2\,\lambda _f\, \left( \frac{(|D_f|-f^{*})}{|D_f|+(r_1-1)f^{*} } \right) ^2+ 2(1-\lambda _f), \\&P^{FD}_{f^{*} \rightarrow f^{*}-2} =\lambda _f\,\left( \frac{|D_f|-f^{*}}{|D_f|+(r_1-1)f^{*}} \right) ^2 + 2(1-\lambda _f), \\&\mathcal{B}(i) = \sum _{j\ne i} \mathrm{P}^{FD}_{i \rightarrow j}, \quad \text{ for } 1\le i \le |D_f|. \end{aligned}$$

If divisions never occur in the FD compartment, i.e., $\lambda _f=0$, then the number of FD mutants ($d^{*}$) remains constant, implying $\pi ^\mathrm{FD}_{f^{*}} =0$, for $1\le f^{*} \le |D_f|-1$.

1.7 G. The Fixation Probability of Mutant TA and FD Cells in the FD Compartment

In this part, we investigate the probability of the progeny of mutant TA cells taking over the entire FD compartment. We assume that initially there are only $d^{*}$ number of mutant TA cells and $f^{*}$ number of mutant FD cells, i.e., $(e^{*}, b^{*}, d^{*}, f^{*}) = (0,0, d^{*}, f^{*} )$. Following the methods used in the previous sections, we assume that $\pi ^\mathrm{FD}_{(d^{*},f^{*})}$ is the fixation probability of starting from $d^{*}$ number of mutant TA cells and $f^{*}$ number of mutant FDs (initial state is $(d^{*},f^{*})$). We consider a bi-variable Markov chain to explore the cell dynamics in the FD and TA compartments. The fixation probability $\pi ^\mathrm{FD}_{(d^{*}, f^{*})}$ satisfies the following equation.

$$\begin{aligned} \pi ^\mathrm{FD}_{(0,0)}= & {} 0 \nonumber \\ \pi ^\mathrm{FD}_{(d^{*},f^{*})}= & {} \sum _{{\tilde{d^{*}},\tilde{f^{*}}}}\, P_{(d^{*},f^{*})\rightarrow (\tilde{d^{*}},\tilde{f^{*}})}\,\pi ^\mathrm{FD}_{(\tilde{d^{*}},\tilde{f^{*}})} \nonumber \\ \pi ^\mathrm{FD}_{(d^{*}, |D_f|)}= & {} 1 \text { for any } 0\le d^{*} \le |D_t|. \end{aligned}$$

(22)

In order to obtain the fixation probability $\pi ^\mathrm{FD}_{(d^{*},f^{*})}$, we numerically solve the matrix representation of the system of Eq. (22). Note that if $\lambda _f=1$, then there is no chance that mutant TA cells divide, thus $\pi ^\mathrm{FD}_{d^{*},0}=0$ for all $1\le d^{*} \le |D_t|$.

1.8 H. Numerical Simulation

We use the algorithm given in the methods section to do the numerical simulations, and you can find the python code that we used to generate the results in (https://sites.google.com/site/leilishahriyari/FourCompMoranModel_Shahriyari.py?attredirects=0&d=1). In order to obtain the fixation probability and time to fixation through simulations, we set the maximum updating time T equal to 10,000,000 time steps. We run the algorithm for 100 times, and we calculate the ratio of the number of times that fixation occurs over 100. We repeat this process for 10 times to obtain the mean and the standard deviation of the fixation probabilities. Moreover, to obtain the fixation time, we collect the fixation time for each single run whenever the fixation happens. Then, we calculate the average and standard deviation of these collected fixation times. To represent the simulation time steps in terms of days, we assume that the average cell cycle time is 18 hours for mouse and one day for human (Cassimerisz et al. 2011; Potten et al. 1992; Bach 2000). According to Bach (2000), the average cell cycle time of epithelial cells in the mouse crypts is $12-13$ hours for rapidly proliferating cells, and 24 hours for stem cells. Potten et al. (1992) suggested that the human colonic cell cycle is 17–48.6 h. This means that if the total number of cells is N, then we present the time step t as $\frac{t}{N}+1$ day in all simulations done for human crypts in Figs. 4, 5, 6, 7, and 8, and the time step t has been presented as $0.75\frac{t}{N}+1$ day for all simulations done for mouse crypts in Fig. 3.