Ancestral Sequence Reconstruction with Maximum Parsimony

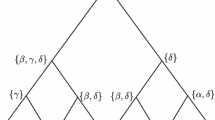
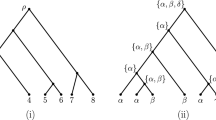
Abstract

One of the main aims in phylogenetics is the estimation of ancestral sequences based on present-day data like, for instance, DNA alignments. One way to estimate the data of the last common ancestor of a given set of species is to first reconstruct a phylogenetic tree with some tree inference method and then to use some method of ancestral state inference based on that tree. One of the best-known methods both for tree inference and for ancestral sequence inference is Maximum Parsimony (MP). In this manuscript, we focus on this method and on ancestral state inference for fully bifurcating trees. In particular, we investigate a conjecture published by Charleston and Steel in 1995 concerning the number of species which need to have a particular state, say a, at a particular site in order for MP to unambiguously return a as an estimate for the state of the last common ancestor. We prove the conjecture for all even numbers of character states, which is the most relevant case in biology. We also show that the conjecture does not hold in general for odd numbers of character states, but also present some positive results for this case.

Appendix

Proof

(Proof of Lemma 1) (i) Let A, B such that $a \in A \cap B$ and $|A| = |B|$. Then A could be transformed into B by renaming all states not element of $A \cap B$. Then $A=B$, and this yields $f_{k,r}^A=f_{k,r}^B$.

(ii) Let $k=0$. In this case, our tree consists of one leaf, which is at the same time the root. This vertex has to be assigned a to obtain $X_\rho =\{a\}$. Hence $f_{0,r}=1$ for all r.

(iii) Let $k \ge 1$. Then

$$\begin{aligned} f_{k,r}&= \min \left\{ f_{k-1,r}^B+f_{k-1,r}^C: B*C=\{a\} \right\} \\&= \min \left\{ f_{k-1,r}^B+f_{k-1,r}^C: B \cap C=\{a\} \right\} , \\&\text {since } B \cup C \text { would not result in } X_\rho =\{a\} \text { as }B,C\ne \emptyset . \end{aligned}$$

Therefore, $a \in B$ and $a \in C$ which results in $f_{k,r} \ge 2$. $\square$

Proof

(Lemma 2) Let $r= 2p\ge 2$, i.e. $p\ge 1$.

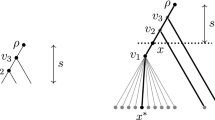
• 1. We start with the case $k\le p$. We have $f_{1,r}=2$ for all r (see Fig. 8). By Theorem 3, we know that $f_{k,r}$ is monotonically increasing in k, and thus, $2=f_{1,r} \le f_{p,r}$. We now use the standard decomposition for $T_p$ in order to derive its two maximal pending rooted subtrees $T_{p-1}$ with roots $\rho _1$ and $\rho _2$. We use the same construction as in the proof of Observation 1, which is depicted in Fig. 6. Thus, we can achieve $X_{\rho _1}=A_p=\{a,c_1, \ldots , c_{p-1}\}$ and $X_{\rho _2}=A_p^{'}=\{a,c_p, \ldots , c_{2p-2}\}$ by assigning a to one leaf in each subtree $T_{p-1}$, respectively, where $R=\{a,c_1,\ldots ,c_{2p-1}\}$, and such that all other subtrees use one state each which is unique to this subtree. Thus, the root of $T_p$ will have the MP root state estimate $A_p \cap A_p^{'}=\{a\}$. (Note that no leaf is assigned character state $c_{2p-1}$; we do not even require all states. We will need this fact later.) We conclude $f_{p,r}\le 2$, which together with $f_{p,r}\ge 2$ as explained above completes $f_{p,r}=2$. Together with Theorem 3, we achieve that $f_{k,r}=2$ for all $k=1,\ldots ,p$.

• 2. Now consider the case $k=p+1$. In this case, we have with (7)

  $$\begin{aligned} f_{p+1,r}=f_{p+1,2p}&=\min \left\{ f_{p,2p}+f_{p,2p}^{A_{2p}},f_{p,2p}^{A_{2}}+f_{p,2p}^{A_{2p-1}},\ldots , f_{p,2p}^{A_{p}}+f_{p,2p}^{A_{p+1}} \right\} \\&=\min \left\{ f_{p,2p}+f_{p,2p}^{A_{2p}},f_{p-1,2p}+f_{p,2p}^{A_{2p-1}},\ldots , f_{1,2p}+f_{0,2p} \right\}&\text {by Theorem } 4 \\&=\min \left\{ 2+f_{p,2p}^{A_{2p}},2+f_{p,2p}^{A_{2p-1}},\ldots , 2+1 \right\}&\text {by Lemma 2, part 1 } \\&=3. \end{aligned}$$

  The latter equation is true because $1 \le f_{p,2p}^{A_{2p}} \le f_{p,2p}^{A_{2p-1}} \le \cdots \le f_{p,2p}^{A_{p+1}}$ (at least one leaf has to be labelled a if a shall appear in the MP root state estimate).

• 3. Now consider the case $k=r$. We can proceed as above and assign $X_{\rho _1}=A_p=\{a,c_1, \ldots , c_{p-1}\}$ to the first of the two $T_{r-1}$ subtrees induced by the standard decomposition, and $X_{\rho _2}=A_{p+1}^{'}=\{a,c_p, \ldots , c_{2p-1}\}$ to the other one, where again $R=\{a,c_1,\ldots ,c_{2p-1}\}$. Then by (7), we can conclude $f_{r,r}\le f_{r-1,r}^{A_p} + f_{r-1,r}^{A_{p+1}}$. Note that $f_{r-1,r}^{A_p} + f_{r-1,r}^{A_{p+1}}= f_{p,r}+f_{p-1,r}$ by Theorem 4, so that $f_{r,r}\le f_{p,r}+f_{p-1,r} = 2+2$, where the latter equation holds because of the first part of Lemma 2. Altogether, $f_{r,r}\le 4$. By the monotonicity of Theorem 3, we obtain $f_{k,r} \le 4$ for all $p+1 < k \le r$. $\square$