Evaluations of Interventions Using Mathematical Models with Exponential and Non-exponential Distributions for Disease Stages: The Case of Ebola

Abstract

Many mathematical models for the disease transmission dynamics of Ebola have been developed and studied, particularly during and after the 2014 outbreak in West Africa. Most of these models are systems of ordinary differential equations (ODEs). One of the common assumptions made in these ODE models is that the duration of disease stages, such as latent and infectious periods, follows an exponential distribution. Gamma distributions have also been used in some of these models. It has been demonstrated that, when the models are used to evaluate disease control strategies such as quarantine or isolation, the models with exponential and Gamma distribution assumptions may generate contradictory results (Feng et al. in Bull Math Biol 69(5):1511–1536, 2007). Several Ebola models are considered in this paper with various stage distributions, including exponential, Gamma and arbitrary distributions. These models are used to evaluate control strategies such as isolation (or hospitalization) and timely burial and to identify potential discrepancies between the results from models with exponential and Gamma distributions.

Appendices

Appendix 1: Derivation of $p_c$ for Model C

Recall that in Model C (see (30)), $T_{P_c}$ and $T_{L_c}$ follow exponential distributions with parameters $\gamma$ and $\chi$, respectively (for ease of notation the subscripts have been dropped), and $T_{M_c}$ follows Gamma distribution with parameters $(\mu , q \mu )$. That is, $P_{c}(t)=G^{1}_{\gamma }$, $L_{c}(t)=G^{1}_{\chi }$, and $M_{c}(t)=G^{q}_{q\mu }$ (G for Gamma with the superscript being the shape parameter). Let $g_X(s)=-\dot{X}(s)$ for $X=P_c, L_c$ and $M_c$. Note that the proportion of infected individuals that are hospitalized is given by

$$\begin{aligned} p_c=p_{H_c}= & {} {\mathbb {P}}[T_{L_{c}}=\min \{T_{P_{c}},T_{L_{c}},T_{M_{c}} \}]\\= & {} \int _{T_{P_{c}},T_{M_{c}}>T_{L_{c}}} g_{P_{c}}(s)g_{M_{c}}(u)g_{L_{c}}(t)\hbox {d}u\hbox {d}t\hbox {d}s\\= & {} \int _0^\infty \int _0^t\int _0^ug_{L_{c}}(s)\hbox {d}sg_{M_{c}}(u)\hbox {d}ug_{P_{c}}(t)\hbox {d}t \quad (T_{P_{c}}\ge T_{M_{c}}\ge T_{L_{c}})\\&+\int _0^\infty \int _0^u\int _0^tg_{L_{c}}(s)\hbox {d}sg_{P_{c}}(t)\hbox {d}tg_{M_{c}}(u)\hbox {d}u \quad (T_{M_{c}}\ge T_{P_{c}}\ge T_{L_{c}}). \end{aligned}$$

Thus,

$$\begin{aligned} p_{H_{c}}= & {} \int _0^\infty \int _0^t\int _0^u\chi \hbox {e}^{-\chi s}\hbox {d}s q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}du\gamma \hbox {e}^{-\gamma t}\hbox {d}t\\&+\int _0^\infty \int _0^u\int _0^t\chi \hbox {e}^{-\chi s}\hbox {d}s\gamma \hbox {e}^{-\gamma t}dt q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\\= & {} \int _0^\infty \int _0^t\left( 1-\hbox {e}^{-\chi u}\right) q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\gamma \hbox {e}^{-\gamma t}\hbox {d}t\\&+\int _0^\infty \int _0^u\left( 1-\hbox {e}^{-\chi t}\right) \gamma \hbox {e}^{-\gamma t}\hbox {d}t q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\\= & {} \int _0^\infty \int _u^\infty \gamma \hbox {e}^{-\gamma t}\hbox {d}t\left( 1-\hbox {e}^{-\chi u}\right) q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\\&+\int _0^\infty \int _0^u\left( 1-\hbox {e}^{-\chi t}\right) \gamma \hbox {e}^{-\gamma t}\hbox {d}t q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\\= & {} \int _0^\infty \left[ 1-\hbox {e}^{-\gamma u}-\frac{\gamma }{\gamma +\chi }\left( 1-\hbox {e}^{-(\chi +\gamma )u}\right) \right] q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\\&+\int _0^\infty \hbox {e}^{-\gamma u}\left( 1-\hbox {e}^{-\chi u}\right) q\mu \frac{(q\mu u)^{q-1}\hbox {e}^{-q\mu u}}{(q-1)!}\hbox {d}u\\= & {} \left[ 1-\frac{(q\mu )^{q}}{(q\mu +\gamma )^{q}}-\frac{\gamma }{\gamma +\chi }\left( 1-\frac{(q\mu )^{q}}{(q\mu +\gamma +\chi )^{q}}\right) \right] \\&+\left[ \frac{(q\mu )^{q}}{(q\mu +\gamma )^{q}}-\frac{(q\gamma )^{q}}{(\chi +q\mu +\gamma )^{q}}\right] \\= & {} \left( 1-\frac{\gamma }{\gamma +\chi }\right) \left[ 1-(\frac{q\mu }{q\mu +\gamma +\chi })^{q}\right] \\= & {} \frac{\chi }{\chi +\gamma }\left[ 1-\left( \frac{q\mu }{q\mu +\gamma +\chi }\right) ^{q}\right] . \end{aligned}$$

Appendix 2

In this appendix, we provide the detailed derivation for the reduction in the system (7) to an ODE system under the specific survival functions given in (10) and (11).

Using these functions and from the I equation in (7), we obtain

$$\begin{aligned} I(t)= & {} \displaystyle \int _0^t\alpha E(s) \sum _{j=1}^n\frac{[n\mu (t-s)]^{j-1}\hbox {e}^{-n\mu (t-s)}}{(j-1)!}\hbox {e}^{-\chi (t-s)}\hbox {e}^{-\gamma (t-s)}\hbox {d}s \nonumber \\&+\,\displaystyle I(0)\sum _{j=1}^n\frac{(n\mu t)^{j-1}\hbox {e}^{-n\mu t}}{(j-1)!} \hbox {e}^{-\chi t}\hbox {e}^{-\gamma t} \nonumber \\= & {} \displaystyle \sum _{j=1}^n\bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1} \hbox {e}^{-(n\mu +\chi +\gamma )(t-s)}}{(j-1)!}\hbox {d}s \nonumber \\&+\,\displaystyle I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\chi +\gamma ) t}}{(j-1)!} \bigg ]. \end{aligned}$$

(39)

Let

$$\begin{aligned} I_{j}(t)&\doteq \displaystyle \int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1} \hbox {e}^{-(n\mu +\chi +\gamma )(t-s)}}{(j-1)!}\hbox {d}s\nonumber \\&\quad + \displaystyle I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\chi +\gamma ) t}}{(j-1)!}, \end{aligned}$$

(40)

for $j=1,2,\ldots ,n$. Then from (39) and (40),

$$\begin{aligned} I(t)=\sum _{j=1}^n I_{j}(t). \end{aligned}$$

(41)

Differentiating $I_j(t)$ in (40), we arrive at

$$\begin{aligned} I_1'(t)=\alpha E(t)-(\gamma +\chi +n\mu )I_1, \end{aligned}$$

(42)

and

$$\begin{aligned} I_{j}'(t)&=\displaystyle -(\gamma +\chi )\bigg [\int _0^t\alpha E(s) \frac{[n\mu (t-s)]^{j-1}\hbox {e}^{-(n\mu +\chi +\gamma )(t-s)}}{(j-1)!}\hbox {d}s \\&\quad \displaystyle +I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\chi +\gamma ) t}}{(j-1)!}\bigg ] \\&\quad +\displaystyle n\mu \bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-2} \hbox {e}^{-(n\mu +\chi +\gamma )(t-s)}}{(j-2)!}\hbox {d}s\\&\quad + I(0)\frac{(n\mu t)^{j-2} \hbox {e}^{-(n\mu +\chi +\gamma ) t}}{(j-2)!}\bigg ]\\&\quad \displaystyle -n\mu \bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1}\hbox {e}^{-(n\mu +\chi +\gamma )(t-s)}}{(j-1)!}\hbox {d}s\\&\quad + I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\chi +\gamma ) t}}{(j-2)!} \bigg ]. \end{aligned}$$

It follows that

$$\begin{aligned} I_j'(t)= n\mu I_{j-1}(t)-(\gamma +\chi +n\mu )I_{j}(t), \quad j=2,3,\ldots ,n. \end{aligned}$$

(43)

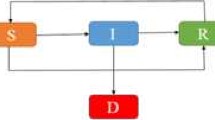
The above derivation indicates that the assumption of $T_M$ being Gamma leads to the fact that the I class can be divided into n subclasses, denoted by $I_j$ for $1 \le j \le n$, while each substage j can be described by an exponential distribution with parameter $n\mu$ (see the transition diagram Fig. 2).

Let

$$\begin{aligned} H_{j}(t)\doteq & {} \displaystyle \int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1} \hbox {e}^{-(n\mu +\gamma )(t-s)}}{(j-1)!}\Big [1-\hbox {e}^{-\chi (t-s)}\Big ]\hbox {d}s \nonumber \\&+ \displaystyle I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(j-1)!}\Big (1-\hbox {e}^{-\chi t}\Big ), \quad j=1,2,\ldots ,n. \end{aligned}$$

(44)

Using the H equation in (7) and the M function in (11), we have

$$\begin{aligned} H(t)= & {} \int _0^t\alpha E(s)\sum _{j=1}^n\frac{[n\mu (t-s)]^{j-1}\hbox {e}^{-n\mu (t-s)}}{(j-1)!}\left[ 1-\hbox {e}^{-\chi (t-s)}\right] \hbox {e}^{-\gamma (t-s)}\hbox {d}s\\&+I(0)\sum _{j=1}^n\frac{(n\mu t)^{j-1}\hbox {e}^{-n\mu t}}{(j-1)!}\left( 1-\hbox {e}^{-\chi t}\right) \hbox {e}^{-\gamma t}\\= & {} \displaystyle \sum _{j=1}^n\bigg [ \int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1} \hbox {e}^{-(n\mu +\gamma )(t-s)}}{(j-1)!}\Big [1-\hbox {e}^{-\chi (t-s)}\Big ]\hbox {d}s \\&+ \displaystyle I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(j-1)!}\Big (1-\hbox {e}^{-\chi t}\Big )\bigg ]. \end{aligned}$$

It follows from (44) that

$$\begin{aligned} H(t)=\displaystyle \sum _{j=1}^n H_{j}(t). \end{aligned}$$

(45)

Differentiating $H_j$ in (44) we have

$$\begin{aligned} H_{1}'(t)= -(\gamma +n\mu )H_{1}(t)+\chi I_{1}(t) \end{aligned}$$

(46)

and

$$\begin{aligned} H_{j}'(t)= & {} -\big (\gamma +n \mu \big )\bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1} \hbox {e}^{-(n\mu +\gamma )(t-s)}}{(j-1)!}\Big [1-\hbox {e}^{-\chi (t-s)}\Big ]\hbox {d}s\\&+\,I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(j-1)!}\left( 1-\hbox {e}^{-\chi t}\right) \bigg ]\\&+\,n\mu \bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-2} \hbox {e}^{-(n\mu +\gamma )(t-s)}}{(j-2)!}\left[ 1-\hbox {e}^{-\chi (t-s)}\right] \hbox {d}s\\&+\,I(0)\frac{(n\mu t)^{j-2}\hbox {e}^{-(n\mu +\gamma ) t}}{(j-2)!}(1-\hbox {e}^{-\chi t})\bigg ]\\&+\,\chi \bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{j-1}\hbox {e}^{-(n\mu +\gamma )(t-s)}}{(j-1)!} \hbox {e}^{-\chi (t-s)}\hbox {d}s\\&+\,I(0)\frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(j-1)!}\hbox {e}^{-\chi t}\bigg ], \quad j>1. \end{aligned}$$

It follows that

$$\begin{aligned} H'_j(t)=n\mu H_{j-1}(t)+\chi I_{j}(t)-(\gamma +n\mu )H_{j}(t), \quad j=2, 3, \ldots , n. \end{aligned}$$

(47)

The derivation of the equations for $H_j$ indicates that the H class can also be divided into n subclasses, denoted by $H_j$ for $1 \le j \le n$, and each substage j can be described by an exponential distribution with parameter $n\mu$ (see the transition diagram Fig. 2).

For the D equation, we can use the density function $g_M(s)$ in (11) to get

$$\begin{aligned} D(t)= & {} \int _0^t\left[ \int _0^\tau \alpha E(s)P(\tau -s)g_{M}(\tau -s)ds+I(0)P(\tau )g_{M}(\tau )\right] \hbox {e}^{-\gamma _{f}(\tau -s)}\hbox {d}\tau \\= & {} \int _0^t\bigg \{\int _0^\tau \alpha E(s)n\mu \frac{[n\mu (\tau -s)]^{n-1}\hbox {e}^{-(n\mu +\gamma )(\tau -s)}}{(n-1)!}\hbox {d}s\\&+I(0)n\mu \frac{(n\mu \tau )^{n-1}\hbox {e}^{-(n\mu +\gamma )\tau }}{(n-1)!}\bigg \} \hbox {e}^{-\gamma _{f}(t-\tau )}\hbox {d}\tau . \end{aligned}$$

Differentiation of the above equation leads to

$$\begin{aligned} D'(t)= & {} n\mu \bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{n-1} \hbox {e}^{-(n\mu +\gamma )(t-s)}}{(n-1)!}\Big [1-\hbox {e}^{-\chi (t-s)}\Big ]\hbox {d}s\\&+\,I(0)\frac{(n\mu t)^{n-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(n-1)!}\Big (1-\hbox {e}^{-\chi t}\Big ) \bigg ]\\&+\,n\mu \bigg [\int _0^t\alpha E(s)\frac{[n\mu (t-s)]^{n-1}\hbox {e}^{-(n\mu +\gamma )(t-s)}}{(n-1)!}\hbox {e}^{-\chi (t-s)}\hbox {d}s\\&+\,I(0)\frac{(n\mu t)^{n-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(n-1)!}\hbox {e}^{-\chi t}\bigg ]-\gamma _{f}D, \end{aligned}$$

and from (40) and (44),

$$\begin{aligned} D'(t)=n\mu I_{n}(t)+n\mu H_{n}(t)-\gamma _{f}D(t). \end{aligned}$$

(48)

Similarly, for the R equation, note that

$$\begin{aligned} R(t)= & {} \int _0^t\left[ \int _0^\tau \alpha E(s)M(\tau -s)g_{P}(\tau -s)\hbox {d}s+I(0)M(\tau )g_{P}(\tau )\right] \hbox {d}\tau \\= & {} \int _0^t\bigg [\int _0^\tau \alpha E(s)\gamma \sum _{j=1}^n \frac{[n\mu (\tau -s)]^{j-1} \hbox {e}^{-(n\mu +\gamma )(\tau -s)}}{(j-1)!}\hbox {d}s\\&+\,I(0)\gamma \sum _{j=1}^n\frac{(n\mu \tau )^{j-1} \hbox {e}^{-(n\mu +\gamma )\tau }}{(j-1)!}\bigg ]\hbox {d}\tau \\= & {} \sum _{j=1}^n\bigg \{\int _0^t\bigg [\int _0^\tau \alpha E(s)\gamma \frac{[n\mu (\tau -s)]^{j-1} \hbox {e}^{-(n\mu +\gamma )(\tau -s)}}{(j-1)!}\hbox {d}s\\&+\,I(0)\gamma \frac{(n\mu \tau )^{j-1}\hbox {e}^{-(n\mu +\gamma )\tau }}{(j-1)!}\bigg ]\hbox {d}\tau \bigg \}. \end{aligned}$$

Then,

$$\begin{aligned} R'(t)= & {} \displaystyle \sum _{j=1}^n \bigg [ \int _0^t\alpha E(s)\gamma \frac{[n\mu (t-s)]^{j-1} \hbox {e}^{-(n\mu +\gamma )(t-s)}}{(j-1)!}\Big [1-\hbox {e}^{-\chi (t-s)}\Big ]\hbox {d}s \\&+\,\displaystyle I(0)\gamma \frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\gamma ) t}}{(j-1)!}\left( 1-\hbox {e}^{-\chi t}\right) \bigg ]\\&+\,\displaystyle \sum _{j=1}^n \bigg [ \int _0^t\alpha E(s)\gamma \frac{[n\mu (t-s)]^{j-1}\hbox {e}^{-(n\mu +\gamma +\chi )(t-s)}}{(j-1)!} \\&\displaystyle +\,I(0)\gamma \frac{(n\mu t)^{j-1}\hbox {e}^{-(n\mu +\gamma +\chi ) t}}{(j-1)!} \bigg ]. \end{aligned}$$

It follows from (40), (41), (44) and (45) that

$$\begin{aligned} R'(t)=\gamma H(t)+\gamma I(t). \end{aligned}$$

(49)

From the differential Eqs. (42), (43), (46), (47), (48) and (49), we arrive at the ODE model (22).

When M(s) is also an exponential function, i.e., when $n=1$, the system (22) is further reduced to the following system (which is also the special case of model (9) when $n=1$):

$$\begin{aligned} \displaystyle \frac{\hbox {d}S}{\hbox {d}t}&=-\frac{1}{N}S\Big (\beta _{I} I+\beta _{H} H+\beta _{D}D\Big ), \nonumber \\ \displaystyle \frac{\hbox {d}E}{\hbox {d}t}&=\frac{1}{N}S\Big (\beta _{I} I+\beta _{H} H +\beta _{D}D\Big )-\alpha E,\nonumber \\ \displaystyle \frac{\hbox {d}I}{\hbox {d}t}&=\alpha E-(\chi +\gamma +\mu )I,\nonumber \\ \displaystyle \frac{\hbox {d}H}{\hbox {d}t}&=\chi I-(\gamma +\mu )H,\nonumber \\ \displaystyle \frac{\hbox {d}D}{\hbox {d}t}&=\mu I+\mu H-\gamma _{f}D,\nonumber \\ \displaystyle \frac{\hbox {d}R}{\hbox {d}t}&=\gamma I+ \gamma H. \end{aligned}$$

(50)