Stabilizing Control for a Pulsatile Cardiovascular Mathematical Model

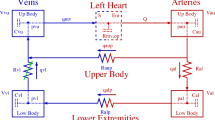
Abstract

In this paper, we develop a pulsatile model for the cardiovascular system which describes the reaction of this system to a submaximal constant workload imposed on a person at a bicycle ergometer test after a period of rest. Furthermore, the model should allow to use measurements for the pulsatile pressure in fingertips which provide information on the diastolic and the systolic pressure for parameter estimation. Based on the assumption that the baroreceptor loop is the essential control loop in this case, we design a stabilizing feedback control for the pulsatile model which is obtained by solving a linear-quadratic regulator problem for the linearization of a non-pulsatile counterpart of the pulsatile model. We also investigate the behavior of the model with respect to changes in the weight of the term in the cost functional for the linear-quadratic regulator problem which penalizes the deviation of the momentary pressure in the aorta from the pressure at the stationary situation which should be obtained.

Appendices

Appendix 1: Parameter Values used in the Model

The following tables provide the parameter names, meanings, and values used in the simulation. The values listed in Tables 1 and 2 are taken from the literature (Batzel et al. 2007; Kappel and Peer 1993) with some modifications for the parameters of the finger compartment. The associated units are also given.

Table 1 Parameter values

For the computation of the feedback control law, we need constant approximations $x^{\text {rest}}$ and $x^{\text {exer}}$ of the solutions which correspond to the stationary phases “rest” and “exercise” (see Sect. 3). This is done in Appendix 2 using the corresponding workload $W^{\text {equil}}$, the corresponding value $H^{\text {equil}}$ of the heart frequency and the corresponding value $A_{\text {pesk}}^{\text {equil}}$ of Peskin’s constant in Eq. (11). In Table 2, we list the values for $H^{\text {equil}},\, W^{\text {equil}}$, and $A_{\text {pesk}}^{\text {equil}}$.

Table 2 Parameters for the stationary phases

Appendix 2: Determination of Equilibria

The feedback law (27) for the pulsatile model (15) obtained in Section 3 requires the vector $\bigl ((x^{\text {exer}})^{\mathsf{T}},S_{\ell \text {v}}^{\text {exer}},\sigma _{\ell \text {v}}^{\text {exer}}\bigr )^{\mathsf{T}}$. Furthermore, we also need the vector $\bigl ((x^{\text {rest}})^{\mathsf{T}},$ $S_{\ell \text {v}}^{\text {rest}},\sigma _{\ell \text {v}}^{\text {rest}}\bigr )^{\mathsf{T}}$ as initial condition for the model (15) and (28). In contrast to the non-pulsatile model where ${\tilde{x}}^{\text {rest}}$ and ${\tilde{x}}^{\text {exer}}$ are equilibrium solutions corresponding to the stationary situations “rest” and “exercise,” we have periodic solutions of the pulsatile model which characterize the stationary situations “rest” and “exercise.” This can be seen by numerical computations over sufficiently long-time intervals. Let the exponent “equil” stand for “rest,” respectively, for “exer”. In order to compute $x^{\text {equil}}$, we fix $H(t)\equiv H^{\text {equil}},\, W=W^{\text {equil}}$, and $A_{\text {pesk}}=A_{\text {pesk}}^{\text {equil}}$ (as given in Table 2). Moreover, we also fix $S_{\text {rv}}(t)\equiv (\beta _{\text {rv}}/\alpha _{\text {rv}})H^{\text {equil}},\, \sigma _{\text {rv}}(t)\equiv 0$, and $S_{\ell \text {v}}(t)\equiv (\beta _{\ell \text {v}}/\alpha _{\ell \text {v}})H^{\text {equil}},\, \sigma _{\ell \text {v}}(t)\equiv 0$. Then, we compute the solution of system (15) with $u(t)\equiv 0$ and given initial values where $S_{\text {rv}}(0)=S_{\text {rv}}^{\text {equil}}$, and $\sigma _{\text {rv}}(0)=0$. Note that the equations involving $S_{\text {rv}},\, \sigma _{\text {rv}},\, S_{\ell \text {v}}$ and $\sigma _{\ell \text {v}}$ are automatically satisfied. For the various pressures $P_{\dots }$, we take the mean values according to the following formula (see Klabunde 2011):

$$\begin{aligned} P_{\dots }^{\text {equil}}=P_{\dots ,\text {mean}}=P_{\dots ,\text {diast}} + \frac{1}{3}\left( P_{\dots ,\text {syst}}-P_{\dots ,\text {diast}}\right) , \end{aligned}$$

(29)

where $P_{\dots ,\text {diast}}$ and $P_{\dots ,\text {syst}}$ are the end-diastolic and end-systolic pressures, respectively, taken at the last heart period computed. Of course, $P_{\text {vp}}(t)$ is computed using (14). For the resistance $R_{\text {sp}}^{\text {equil}}$, we just take the average of the values for $R_{\text {sp}}(t)$ over the last heart period computed (there are hardly any oscillations visible in the function $R_{\text {sp}}(t)$). Table 3 presents the initial values chosen for the computations and the values for $x^{\text {equil}},\, S_{\ell \text {v}}^{\text {equil}},\, \sigma _{\ell \text {v}}^{\text {equil}}$. The values obtained for the stationary phase “rest” are used as initial values for the computations in case of the phase “exercise” with the exception of $P_{\ell \text {v}},\, S_{\text {rv}},\, \sigma _{\text {rv}},\,S_{\ell \text {v}}$, and $\sigma _{\ell \text {v}}$.

Table 3 Initial and equilibrium mean values during rest and exercise condition

Appendix 3: The Linear-Quadratic Regulator Problem

For the convenience of the reader, we formulate in this appendix the autonomous linear-quadratic regulator problem (LQRP) with infinite time horizon and the main result for this problem. For details, we refer to Kwakernaak and Sivan (1972); Lenhart and Workman (2007); Sontag (1998); Zabczyk (2007). The component “linear” refers to the fact that a linear control system is given, i.e., we have the following equations:

$$\begin{aligned} \frac{ {\hbox {d}}}{{{\hbox {d}}}t}x(t)&= {\mathcal {A}}x(t)+{\mathcal {B}}u(t), \nonumber \\ x(0)&= x_0\in \hbox {I}\!\hbox {R}^n, \nonumber \\ y(t)&= {\mathcal {C}}x(t),\quad t \ge 0, \end{aligned}$$

(30)

where $x(t)\in \hbox {I}\!\hbox {R}^n,\, u(t)\in \hbox {I}\!\hbox {R}^m,\, y(t)\in \hbox {I}\!\hbox {R}^k$, and $\mathcal {A},\, \mathcal {B},\, \mathcal {C}$ are constant matrices of appropriate dimension and $u(\cdot )\in L^2(0,\infty ;\hbox {I}\!\hbox {R}^m)$. We denote the solution of (30) by $x(t)=\bigl (x(t;x_0,u(\cdot )\bigr )$ and define the quadratic cost functional $J$ by

$$\begin{aligned} J(u(\cdot ))=\mathop \int \limits _{0}^{\infty }\!\left( y(t)^{\mathsf{T}}y(t) + u(t)^{\mathsf{T}}Ru(t)\right) \,\mathrm{d}t,\quad u\in L^2(0,\infty ;\hbox {I}\!\hbox {R}^m), \end{aligned}$$

where $y(t)=\mathcal {C}x\bigl (t;x_0,u(\cdot )\bigr ),\, t\ge 0$, and $R\in \hbox {I}\!\hbox {R}^{m\times m}$ is a positive definite matrix. The component “quadratic” in LQRP refers to the fact that we seek a function $\hat{u}(\cdot )\in L^2(0,\infty ;\hbox {I}\!\hbox {R}^m)$ such that the quadratic cost functional $J(u(\cdot ))$ is minimized, i.e.,

$$\begin{aligned} J(\hat{u})=\min _{u\in L^2(0,\infty ;\hbox {I}\!\hbox {R}^m)}J(u). \end{aligned}$$

From control theory (see for instance, Kwakernaak and Sivan 1972), it follows that under some conditions on the matrices $\mathcal {A},\, \mathcal {B}$, and $\mathcal {C}$, the solution of the infinite time horizon LQRP is given by a linear, time-independent feedback law,

$$\begin{aligned} \hat{u}(t)=-{\mathcal {G}}x(t), \quad t \ge 0\ , \end{aligned}$$

(31)

where $x(t)$ is the solution of the closed-loop system

$$\begin{aligned} \frac{\hbox {d}}{{\hbox {d}}t}x(t)&= ({\mathcal {A}}-{\mathcal {B}}{\mathcal {G}})x(t),\quad t \ge 0,\nonumber \\ x(0)&= x_0. \end{aligned}$$

(32)

The feedback matrix $\mathcal {G}\in \hbox {I}\!\hbox {R}^{m\times n}$ is given as $\mathcal {G}=-R^{-1}\mathcal {B}^{\mathsf{T}}\mathcal {X}$, and $\mathcal {X}\in \hbox {I}\!\hbox {R}^{n\times n}$ is the solution of the algebraic Riccati matrix equation

$$\begin{aligned} \mathcal {X}\mathcal {A}+\mathcal {A}^{\mathsf{T}}\mathcal {X}-\mathcal {X}\mathcal {B}R^{-1}\mathcal {B}^{\mathsf{T}}\mathcal {X}+\mathcal {C}^{\mathsf{T}}\mathcal {C}=0. \end{aligned}$$

(33)

The algebraic Riccati equation has a unique positive definite solution $\mathcal {X}$ if the pair $(\mathcal {A},\mathcal {B})$ is stabilizable and the pair $(\mathcal {C},\mathcal {A})$ is detectable (see Kwakernaak and Sivan 1972). Controllability of $(\mathcal {A},\mathcal {B})$ and observability of $(\mathcal {C},\mathcal {A})$ provide stronger conditions requiring

$$\begin{aligned}&\mathrm{rank }\left( \mathcal {B},\mathcal {A}\mathcal {B},\ldots ,\mathcal {A}^{n-1}\mathcal {B}\right) =n\quad \text {and}\\&\mathrm{rank }\left( \mathcal {C}^{\mathsf{T}},\mathcal {A}^{\mathsf{T}}\mathcal {C}^{\mathsf{T}},\ldots ,\bigl (\mathcal {A}^{\mathsf{T}}\bigr )^{n-1}\mathcal {C}^{\mathsf{T}}\right) =n. \end{aligned}$$

Under these conditions the closed-loop system (32) is globally asymptotically stable, i.e., all eigenvalues of the matrix $\mathcal {A}-\mathcal {B}\mathcal {G}$ have a negative real part.

Assume that the linear system (30) is obtained from a non-linear system

$$\begin{aligned} \frac{\hbox {d}}{{\hbox {d}}t}&= {\mathcal {F}}\bigl (x(t),u(t)\bigr ), \nonumber \\ x(0)&= x_0\in \hbox {I}\!\hbox {R}^n, \nonumber \\ y(t)&= h(x(t)),\quad t \ge 0, \end{aligned}$$

(34)

by linearization around an equilibrium $x_{\text {equi}}$ and around $u\equiv 0$. The system of equations for computing $x_{\text {equi}}$ is

$$\begin{aligned} \mathcal {F}\bigl (x_{\text {equi}},0\bigr )=0. \end{aligned}$$

Without restriction we can assume $h(x_{\text {equi}})=0$ (otherwise we replace $h(x)$ by $h(x)-h(x_{\text {equi}})$). Then, the matrices $\mathcal {A},\, \mathcal {B}$, and $\mathcal {C}$ are given by

$$\begin{aligned} \mathcal {A}=\frac{\partial \mathcal {F}(x,u)}{\partial x}\bigl |_{(x,u)=(x_{\text {equi}},0)},\quad \mathcal {B}=\frac{\partial \mathcal {F}(x,u)}{\partial u}\bigl |_{(x,u)=(x_{\text {equi}},0)},\quad \mathcal {C}=\frac{\partial h}{\partial x}\bigl |_{x=x_{\text {equi}}}. \end{aligned}$$

Then, a result by Russel ((Russell 1979, Chapter IV)) implies that $\hat{u}(t)=-\mathcal {G}\bigl (x(t)-x_{\text {equi}}\bigr )$ is a stabilizing control for the non-linear system (34), i.e., the equilibrium $x(t)\equiv x_{\text {equi}}$ is asymptotically stable (but in general not globally asymptotically stable) for the nonlinear closed-loop system

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}&= \mathcal {F}\bigl (x(t),-\mathcal {G}(x(t)-x_{\text {equi}})\bigr ),\\ x(0)&= x_0\in \hbox {I}\!\hbox {R}^n,\\ y(t)&= h(x(t)),\quad t\ge 0. \end{aligned}$$