The Impact of Cell Density and Mutations in a Model of Multidrug Resistance in Solid Tumors

Abstract

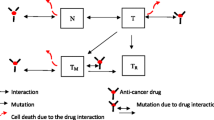
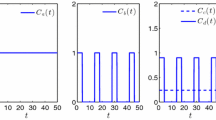
In this paper we develop a mathematical framework for describing multidrug resistance in cancer. To reflect the complexity of the underlying interplay between cancer cells and the therapeutic agent, we assume that the resistance level is a continuous parameter. Our model is written as a system of integro-differential equations that are parameterized by the resistance level. This model incorporates the cell density and mutation dependence. Analysis and simulations of the model demonstrate how the dynamics evolves to a selection of one or more traits corresponding to different levels of resistance. The emerging limit distribution with nonzero variance is the desirable modeling outcome as it represents tumor heterogeneity.

Appendix A

Proposition 1

Consider the integro-differential equation (6). If n(x,0)≥0 for all x∈[0,1], then

$$n(x,t) \geq 0 \quad \forall t \in \mathbb{R}_{+}. $$

Proof

The global existence of continuously differentiable solutions of (1) can be obtained following standard arguments (see Perthame, 2007). For the positivity of n, since n≥0 at t=0, due to its continuity, if there exists a t _∗ for which n(x,t _∗)=0 for some x∈[0,1] (and n(x,t)>0 for t<t _∗), then n(y,t _∗)≥0 for all y. Hence, by (6),

$$\begin{aligned} \frac{\partial n(x,t_{*})}{\partial t} = \theta \int_0^1 \! r(y)M(y,x)n(y,t_{*}) \, \mathrm{d} y \geq 0, \end{aligned}$$

(32)

which implies that n(x,t _∗) is nondecreasing at t _∗. Consequently, n(x,t) cannot pass through 0, as stated. □

Proof of Theorem 1

We follow the proof of Lorz et al. (2013), Lemma 2.2. Consider system (8). If r(x)−c(x)−d(x)<0 for all x∈[0,1], then due to the positivity of n(x,t), $\frac{\partial n(x,t)}{\partial t} < 0$ for all x∈[0,1]. Hence, $n(x,t) \xrightarrow[t \rightarrow \infty]{} 0$ in [0,1]. By Lebesgue’s Dominated Convergence Theorem, this implies that ρ(t)→0 as t→∞.

If, on the other hand, there exists x _∗ such that r(x _∗)−c(x _∗)−d(x _∗)=0, then these are fixed points of (8), and hence,

$$n(x_{*},t)=n(x_{*},0) \quad \forall t \in \mathbb{R}_{+}. $$

Now suppose that there exists x∈[0,1] such that r(x)−c(x)−d(x)>0. By the continuity of the growth parameters and the compactness of [0,1], r(x)−c(x)−d(x) achieves its maximum, say at $\{x_{i} \}_{i=1}^{m}$. We note that it is possible that m=∞, or even that the set $\{x_{i} \}_{i=1}^{m}$ is uncountable (in which case our notation should be altered).

To see that $\rho(t) \xrightarrow[t \rightarrow \infty]{} \infty$, fix $x_{j} \in \{x_{i} \}_{i=1}^{m}$ such that n(x _j ,0)>0 (as the points where n=0 do not contribute to the growth). Then for all 0<λ<r(x _j )−c(x _j )−d(x _j ), there exists γ _λ such that

$$r(x)-c(x)-d(x) \geq \lambda >0 \quad \forall x \in [x_{j}- \gamma_{\lambda},x_{j}+\gamma_{\lambda}]. $$

Let $h_{\lambda}(t) := \int_{x_{j}-\gamma_{\lambda}}^{x_{j}+\gamma_{\lambda}} \! n(x,t) \, \mathrm{d} x$. Then

$$\frac{d}{dt} h_{\lambda}(t) = \int_{x_{j}-\gamma_{\lambda}}^{x_{j}+\gamma_{\lambda}} \! \bigl[r(x)-c(x)-d(x)\bigr]n(x,t) \, \mathrm{d} x \geq \lambda \int _{x_{j}-\gamma_{\lambda}}^{x_{j}+\gamma_{\lambda}} \! n(x,t) \, \mathrm{d} x = \lambda h_{\lambda} (t), $$

so that, for a positive constant h(0),

$$\begin{aligned} h_{\lambda}(t) \geq h(0)e^{\lambda t}. \end{aligned}$$

(33)

As $\rho(t) = \int_{0}^{1} \! n(x,t) \, \mathrm{d} x \geq h_{\lambda}(t)$, (33) implies that $\rho(t) \xrightarrow[t \rightarrow \infty]{} \infty$, as desired. To find the limiting distribution, note that for $x \notin \{x_{i} \}_{i=1}^{m}$, choose λ such that

$$r(x)-c(x)-d(x) < \lambda < r(x_{j})-c(x_{j})-d(x_{j}). $$

Then,

$$\begin{aligned} \frac{n(x,t)}{\rho(t)}=\frac{n(x,0)e^{[r(x)-c(x)-d(x)]t}}{\rho(t)} \leq \frac{n(x,0)}{h(0)} e^{[r(x)-c(x)-d(x)-\lambda]t} \xrightarrow[t \rightarrow \infty]{} 0. \end{aligned}$$

(34)

As $\int_{0}^{1} \! \frac{n(x,t)}{\rho(t)} \, \mathrm{d} x = 1$, for all time t, we have the desired result, namely

$$\lim_{t \rightarrow \infty} \frac{n(x,t)}{\rho(t)}=\sum _{i=1}^{m} a_{i} \delta(x-x_{i}), $$

with $\sum_{i=1}^{m} a_{i} = 1$. If the number of maximizers is uncountable, a similar result will hold for a continuous measure. □

Proof of Theorem 2

Let n(x,t) satisfy (16). By Proposition 1, since n(x,t)≥0, ρ(t)≥0 as well. Let r _M ,c _m , and d _m be constants such that r(x)≤r _M , c(x)≥c _m >0, and d(x)≥d _m >0, and recall that G≥0. Hence, ρ′(t) can be bounded above by

$$\frac{d \rho(t)}{dt} = \int_0^1 \! \bigl[r(x)-c(x)-G\bigl(\rho(t)\bigr)d(x)\bigr]n(x,t) \, \mathrm{d} x \leq \bigl[r_{M}-c_{m}-G\bigl(\rho(t)\bigr)d_{m}\bigr] \rho(t). $$

Since $G(\rho) \xrightarrow[\rho \rightarrow \infty]{} \infty$, there exists ρ _M such that ρ(0)≤ρ _M and r _M −c _m −G(ρ _M )d _m <0. This implies that at ρ=ρ _M , ρ′(t)<0, and hence ρ(t)≤ρ _M . □