The Effect of Time Delay in a Two-Patch Model with Random Dispersal

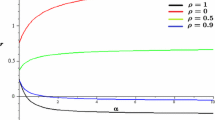
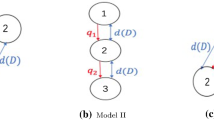
Abstract

We consider a two-patch model for a single species with dispersal and time delay. For some explicit range of dispersal rates, we show that there exists a critical value τ _c for the time delay τ such that the unique positive equilibrium of the system is locally asymptotically stable for τ∈[0,τ _c ) and unstable for τ>τ _c .

Appendices

Appendix A

In this part, we display the main steps of using the center manifold theorem and the normal form method to analyze the stability and the bifurcating direction of the bifurcating periodic orbits for Neumann boundary problem (5). See the details in Hassard et al. (1981), Liao et al. (2012), Yu and Cao (2006). Herein, we use the supremum norm ∥ϕ∥=sup_{−τ≤θ≤0}|ϕ(θ)|. Hence, the phase space $\mathcal{C}:=\mathcal {C}([-\tau,0],\mathbb{R}^{2 })$ is a Banach space of continuous functions.

Denote the solution of (5) as ${\mathbb{U}}(t)= (u_{1}(t), u_{2}(t))^{T}$, and set ${\mathbb{U}}_{t}(\theta)={\mathbb{U}}(t+\theta)$, θ∈[−τ,0], ν:=τ−τ _c , where T denotes the transpose. Then, we can rewrite (11) in the form

$$ \dot{{\mathbb{U}}}(t)=L_{\nu}({\mathbb{U}}_{t})+G_{\nu}({\mathbb{U}}_{t}), $$

(100)

with the linear operator $L_{\nu}:\mathcal{C}\rightarrow \mathbb{R}^{2}$ and the nonlinear operator $G_{\nu}:\mathcal {C}\rightarrow\mathbb{R}^{2}$. More precisely, L _ν  is defined by

$$L_{\nu}(\phi)=M_{0}\phi(0)+M_{1}\phi(- \tau), $$

with

$$ M_{0}=\left ( \begin{array}{c@{\quad}c} -d+\mu(r_1-a) & d\\ d & -d+\mu(r_2-b) \end{array} \right ),\qquad M_{1}=\left ( \begin{array}{c@{\quad}c} -\mu a & 0\\ 0 & -\mu b \end{array} \right ). $$

(101)

In addition, by using the steady-state system (14), M ₀ can be rewritten as

$$\begin{aligned} M_{0}=\left ( \begin{array}{c@{\quad}c} -bd/a & d\\ d & -ad/b \end{array} \right ). \end{aligned}$$

(102)

We can choose

$$\eta(\theta,\nu)= M_{0}\delta(\theta)+M_{1} \delta(\theta+\tau), $$

where δ(⋅) is the Dirac function and η(⋅,μ) is obtained from the Riesz representation theorem, that its entries are functions of bounded variation on [−τ,0] such that

$$ L_{\nu}(\phi)=\int_{-\tau}^{0}d \eta(\theta,\nu)\phi(\theta). $$

(103)

On the other hand, the operator $G_{\nu}:\mathcal{C}\rightarrow\mathbb{R}^{2}$ is defined by

$$ G_{\nu}(\phi)=\left ( \begin{array}{c} -\mu\phi_{1}(0)\phi_{1}(-\tau)+\mbox{h.o.t.}\\ -\mu\phi_{2}(0) \phi_{2}(-\tau)+\mbox{h.o.t.} \end{array} \right ). $$

(104)

Next, we define two operators on $\mathcal{C}^{1} := \mathcal{C}^{1}([-\tau ,0],\mathbb{R}^{2})$:

$$\begin{aligned} (A_{\nu}\phi) (\theta) =&\left \{ \begin{array}{l@{\quad}l} d\phi(\theta)/d\theta, & \theta\in[-\tau,0), \\ \int_{-\tau}^{0}d\eta(\zeta,\nu) \phi(\zeta), & \theta=0; \end{array} \right . \end{aligned}$$

(105)

$$\begin{aligned} (R_{\nu}\phi) (\theta) =&\left \{ \begin{array}{l@{\quad}l} 0, & \theta\in[-\tau,0), \\ G_{\nu}(\phi), & \theta=0, \end{array} \right . \end{aligned}$$

(106)

and transform (100) into

$$ \dot{{\mathbb{U}}}_{t}=A_{\nu}{\mathbb{U}}_{t}+R_{\nu}{\mathbb{U}}_{t}. $$

(107)

Note that the adjoint operator $A^{\ast}_{\nu}$ of A _ν is defined as

$$\bigl(A^{\ast}_{\nu}\psi\bigr) \bigl( \theta^{\ast}\bigr)= \left \{ \begin{array}{l@{\quad}l} -d\psi(\theta^{\ast})/d\theta^{\ast}, & \theta^{\ast}\in (0,\tau], \\ \int_{-\tau}^{0}d\eta^{T}(\zeta,\nu)\psi(-\zeta), & \theta^{\ast}=0, \end{array} \right . $$

where $\psi\in\mathcal{C}^{1}([0,\tau],\mathbb{R}^{2})$. For convenience, we allow functions to have range in $\mathbb{C}^{2}$, instead of merely $\mathbb{R}^{2}$, in the following computation.

We define the following bilinear form:

$$\langle\psi,\phi\rangle:=\overline{\psi}^T(0) \phi(0)- \int_{\theta=-\tau}^{0}\int_{\xi=0}^{\theta} \overline{\psi }^{T}(\xi-\theta)\,d\eta(\theta) \phi(\xi)\,d\xi, $$

for $\phi\in\mathcal{C}([-\tau,0],\mathbb{C}^{2})$, $\psi\in\mathcal {C}([0,\tau],\mathbb{C}^{2})$, where η(θ):=η(θ,0), to determine the coordinates of the center manifold near the origin of (100). Note that the overline stands for complex conjugate.

Next, we aim at finding the eigenvectors q(θ) and q ^∗(θ ^∗) of A:=A ₀ and $A^{\ast}:=A^{\ast}_{0}$ with purely imaginary eigenvalues iw _c and −iw _c , respectively; namely,

$$ Aq(\theta)=iw_{c}q(\theta) \quad\mbox{and}\quad A^{\ast}q^{\ast}\bigl(\theta^{\ast}\bigr)=-iw_{c}q^{\ast} \bigl(\theta^{\ast}\bigr), $$

(108)

which satisfy the normalized conditions 〈q ^∗,q〉=1 and $\langle q^{\ast},\bar{q} \rangle=0$. Hence, we set

$$ q(\theta)=q(0)e^{iw_{c}\theta},\qquad q^{\ast}\bigl( \theta^{\ast}\bigr)=q^{\ast }(0)e^{iw_{c}\theta^{\ast}}, $$

(109)

for θ∈[−τ,0), θ ^∗∈(0,τ], and $q(0)=(q_{1}, q_{2})^{T}, q^{\ast}(0)=\frac{1}{\rho}(q_{1}^{\ast}, q^{\ast}_{2})^{T}$, and substitute (109) into (108) at θ=0 to yield

$$\begin{aligned} & q_{1}=1,\qquad q_{2}=\frac{b}{a}+ \frac{1}{d}\bigl(iw_c+\mu a e^{-iw_c\tau}\bigr), \\ & q_{1}^{\ast}=1,\qquad q_{2}^{\ast}= \frac{b}{a}+\frac{1}{d}\bigl(-iw_c+\mu a e^{iw_c \tau}\bigr). \end{aligned}$$

In the sequel, 〈q ^∗,q〉=1 and $\langle q^{\ast},\bar {q}\rangle=0$, if we set

$$ \rho=\overline{q_{1}}q_{1}^{\ast}+ \overline{q_{2}}q_{2}^{\ast}+\bar {J}_1 \tau e^{iw_c \tau}, $$

(110)

where $J_{1}:=-\mu(a q_{1} \overline{q_{1}^{\ast}}+b q_{2} \overline{q_{2}^{\ast}})$.

Next, by using q and q ^∗, we can then construct a coordinate for the center manifold Ω ₀ at ν=0. Denote ${\mathbb{U}}_{t}={\mathbb{U}}_{t}(\theta)=(u_{1,t}(\theta), u_{2,t}(\theta))^{T}$ as a solution of (107), and define

$$\begin{aligned} z(t) :=&\bigl\langle q^{\ast},{\mathbb{U}}_{t}\bigr\rangle , \end{aligned}$$

(111)

$$\begin{aligned} W(t,\theta) :=& {\mathbb{U}}_{t}(\theta)-2 \operatorname{Re} \bigl(z(t)q(\theta )\bigr). \end{aligned}$$

(112)

According to the center manifold reduction, we have $W(t,\theta)= W(z(t),\bar{z}(t),\theta)$ on Ω ₀. By the tangency to the center eigenspace at the equilibrium, we further have

$$ W(t,\theta)= W\bigl(z(t),\bar{z}(t),\theta\bigr)=W_{20}( \theta)\frac {z^{2}(t)}{2}+W_{11}(\theta)z(t)\bar{z}(t)+W_{02}( \theta)\frac{\bar {z}^{2}(t)}{2}+\cdots , $$

(113)

where z and $\bar{z}$ are the local coordinates of the center manifold Ω ₀ in directions q ^∗ and $\overline{{q}^{\ast}}$, respectively.

Accordingly, the solution ${\mathbb{U}}_{t}\in\varOmega_{0}$ of (107), at ν=0, satisfies

$$ \dot{z}(t)=iw_{c}z(t)+g\bigl(z(t),\bar{z}(t)\bigr), $$

(114)

with

$$ g(z,\bar{z})= \overline{q^{\ast}}^{T}(0) G_{0}({\mathbb{U}}_{t})=g_{20} \frac{z^{2}}{2}+g_{11}z\bar{z}+g_{02}\frac {\bar{z}^{2}}{2}+g_{21} \frac{z^{2}\bar{z}}{2}+\cdots, $$

(115)

and

$$ \begin{aligned} g_{20}&=-\frac{2}{\bar{\rho}}e^{-iw_c \tau}\mu\bigl(q_1^2 \overline {q_1^{\ast}}+q_2^2 \overline{q_2^{\ast}}\bigr), \\ g_{11}&=\frac{-\mu}{\bar{\rho}}\bigl(q_1 \overline{q_1}\overline{q_1^{\ast }}+q_2 \overline{q_2}\overline{q_2^{\ast}}\bigr) \bigl(e^{-iw_c \tau}+e^{iw_c \tau }\bigr), \\ g_{02}&=-\frac{2}{\bar{\rho}}e^{iw_c \tau}\mu\bigl(\overline {q_1^{2}}\overline{q_1^{\ast}}+ \overline{q_2^2}\overline{q_2^{\ast}} \bigr), \\ g_{21}&=\frac{-1}{\bar{\rho}}\bigl[\mu\bigl(2 q_1 \overline{q_1^{\ast }}W_{11}^{(1)}(-\tau)\\ &\quad{}+2 e^{-iw_c \tau}\bigl(q_1 \overline{q_1^{\ast }}W_{11}^{(1)}(0)+q_2 \overline{q_2^{\ast}}W_{11}^{(2)}(0)+2 q_2 \overline{q_2^{\ast}}W_{11}^{(2)}(- \tau) \\ &\quad{}+\overline{q_1}\overline{q_1^{\ast}}W_{20}^{(1)}(- \tau)+e^{iw_c \tau }\bigl(\overline{q_1} \overline{q_1^{\ast}}W_{20}^{(1)}(0)+ \overline {q_2}\overline{q_2^{\ast}}W_{20}^{(2)}(0) +\overline{q_2}\overline{q_2^{\ast}}W_{20}^{(2)}(- \tau)\bigr)\bigr)\bigr)\bigr], \end{aligned} $$

(116)

where $W_{20}^{(k)}(\theta)$ and $W_{11}^{(k)}(\theta)$ are the kth components of W ₂₀(θ) and W ₁₁(θ), respectively, for −τ≤θ<0. Note that W ₂₀(θ) and W ₁₁(θ) are defined by

$$ \left \{ \begin{array}{l} W_{20}(\theta):=\frac{ig_{20}}{w_{c}}q(0)e^{iw_{c}\theta}-\frac{\bar {g}_{02}}{3iw_{c}}\bar{q}(0)e^{-iw_{c}\theta}+E_{1}e^{2iw_{c}\theta},\\ W_{11}(\theta):=\frac{g_{11}}{iw_{c}}q(0)e^{iw_{c}\theta}- \frac{\bar{g}_{11}}{iw_{c}}\bar{q}(0)e^{-iw_{c}\theta}+E_{2}, \end{array} \right . $$

(117)

where

$$\begin{aligned} E_{1} =&\biggl(2iw_{c}I-\int_{-\tau}^{0}e^{2iw_{c}\theta}d \eta(\theta,0)\biggr)^{-1} \left ( \begin{array}{c} -2\mu q_1^{2} e^{-iw_c \tau}\\ -2\mu q_2^{2} e^{-iw_c \tau} \end{array} \right ) \\ =&\left ( \begin{array}{c} \frac{2e^{-iw_c \tau}\mu(-d q_2^2-q_1^2(d\frac{a}{b}+2iw_c+b\mu e^{-2iw_c \tau}))}{-d^2+(d\frac{b}{a}+2iw_c+a\mu e^{-2iw_c \tau})(d\frac{a}{b}+2iw_c+b \mu e^{-2iw_c \tau})}\\ \frac{2 e^{-iw_c \tau}\mu(-d q_1^2-q_2^2(d \frac{b}{a}+2iw_c+a \mu e^{-2iw_c \tau}))}{-d^2+(d\frac{b}{a}+2iw_c+a \mu e^{-2iw_c \tau})(d\frac{a}{b}+2iw_c+b \mu e^{-2iw_c \tau})} \end{array} \right ), \end{aligned}$$

(118)

$$\begin{aligned} E_{2} =&\biggl(-\int_{-\tau}^{0}d\eta( \theta,0)\biggr)^{-1} \left ( \begin{array}{c} -\mu q_1 \overline{q_1}(e^{-iw_c \tau}+e^{iw_c \tau})\\ -\mu q_2 \overline{q_2}(e^{-iw_c \tau}+e^{iw_c \tau}) \end{array} \right ) \\ =& \left ( \begin{array}{c} -\frac{a e^{-iw_c \tau}(1+e^{2iw_c \tau})(q_1(a d+b^2 \mu)\overline {q_1}+b d q_2 \overline{q_2})}{a^3d+b^3d+a^2 b^2\mu} \\ -\frac{b e^{-iw_c \tau}(1+e^{2iw_c \tau})(a d q_1 \overline{q_1}+q_2(b d+a^2 \mu)\overline{q_2})}{a^3d+b^3d+a^2b^2\mu} \end{array} \right ). \end{aligned}$$

(119)

Accordingly, we already derive all formulas to find the values of g ₂₀,g ₁₁,g ₀₂, and g ₂₁. We can then determine the magnitudes of C ₁(0),ν ₂,ζ ₂, and T ₂.

Appendix B

Comparing with Appendix A, herein we consider the center manifold theorem and the normal form method for Dirichlet boundary problem (6) to analyze the stability and the bifurcating direction of the bifurcating orbits. In space $\mathcal{C}:=\mathcal{C}([-\tau,0],\mathbb{R}^{2 })$ with the supremum norm ∥ϕ∥=sup_{−τ≤θ≤0}|ϕ(θ)|, we denote the solution of (6) as $\tilde{{\mathbb{U}}}(t)= (u_{1}(t), u_{2}(t))^{T}$ and set $\tilde{{\mathbb{U}}}_{t}(\theta)=\tilde{{\mathbb{U}}}(t+~\theta), \theta\in[-\tau, 0]$, and $\nu:=\tau-\tilde{\tau}_{c}$. Then, system (40) can be rewritten as

$$ \dot{\tilde{{\mathbb{U}}}}(t)=\tilde{L}_{\nu}(\tilde{{ \mathbb{U}}}_{t})+\tilde{G}_{\nu}(\tilde{{\mathbb{U}}}_{t}), $$

(120)

with the linear operator $\tilde{L}_{\nu}:\mathcal{C}\rightarrow \mathbb{R}^{2}$ and the nonlinear operator $\tilde{G}_{\nu}:\mathcal {C}\rightarrow\mathbb{R}^{2}$. More precisely, $\tilde{L}_{\nu}$ is defined by

$$\tilde{L}_{\nu}(\phi)=\tilde{M}_{0}\phi(0)+ \tilde{M}_{1}\phi(-\tau), $$

with

$$ \tilde{M}_{0}=\left ( \begin{array}{c@{\quad}c} -2d+\mu(r_1-\tilde{a}) & d\\ d & -2d+\mu(r_2-\tilde{b}) \end{array} \right ),\qquad \tilde{M}_{1}=\left ( \begin{array}{c@{\quad}c} -\mu\tilde{a} & 0\\ 0 & -\mu\tilde{b} \end{array} \right ). $$

(121)

By using the steady-state system (43), we rewrite $\tilde{M}_{0}$ as

$$\begin{aligned} \tilde{M}_{0}=\left ( \begin{array}{c@{\quad}c} -\tilde{b}d/\tilde{a} & d\\ d & -\tilde{a}d/\tilde{b} \end{array} \right ). \end{aligned}$$

(122)

We then choose

$$\tilde{\eta}(\theta,\nu)= \tilde{M}_{0}\tilde{\delta}( \theta)+\tilde {M}_{1}\tilde{\delta}(\theta+\tau), $$

where $\tilde{\delta}(\cdot)$ is the Dirac function and $\tilde{\eta }(\cdot,\mu)$ is obtained from the Riesz representation theorem, that its entries are functions of bounded variation on [−τ,0] such that

$$ \tilde{L}_{\nu}(\phi)=\int_{-\tau}^{0}d \tilde{\eta}(\theta,\nu)\phi (\theta). $$

(123)

On the other hand, the operator $\tilde{G}_{\nu}:\mathcal{C}\rightarrow \mathbb{R}^{2}$ is defined by

$$ \tilde{G}_{\nu}(\phi)=\left ( \begin{array}{c} -\mu\phi_{1}(0)\phi_{1}(-\tau)+\mbox{h.o.t.}\\ -\mu\phi_{2}(0) \phi_{2}(-\tau)+\mbox{h.o.t.} \end{array} \right ). $$

(124)

By using the steady-state systems (14) and (43), the structures of $\tilde{M}_{0}$ in (122) and M ₀ in (102) are totally the same. In addition, the structures of $\tilde{M}_{1}$ and M ₁ are also the same with each other and the formulas of the linear and nonlinear operators $\tilde {L}_{\nu}$ and $\tilde{G}_{\mu}$ of system (120) are very similar to L _μ and G _μ for system (100) in Appendix A. Accordingly, the analysis and formulas in center manifold theorem and the normal form method of these two systems (5) and (6) are almost the same. More precisely, all formulas for system (6) are obtain from replacing the values a,b by $\tilde{a},\tilde{b}$ in Appendix A. Therefore, we omit the details of center manifold theorem and the normal form method for system (6).