Modelling the Use of Wolbachia to Control Dengue Fever Transmission

Abstract

Experiments and field trials have shown that the intracellular bacterium Wolbachia may be introduced into populations of the mosquito Aedes aegypti, the primary vector for dengue fever. In the absence of Wolbachia, a mosquito acquiring the dengue virus from an infected human enters an exposed (infected but not infectious) period before becoming infectious itself. A Wolbachia-infected mosquito that acquires dengue (i) may have a reduced lifespan, so that it is less likely to survive the exposed period and become infectious, and (ii) may have a reduced ability to transmit dengue, even if it has survived the exposed period. Wolbachia introduction has therefore been suggested as a potential dengue control measure. We set up a mathematical model for the system to investigate this suggestion and to evaluate the desirable properties of the Wolbachia strain to be introduced. We show that Wolbachia has excellent potential for dengue control in areas where R ₀ is not too large. However, if R ₀ is large, Wolbachia strains that reduce but do not eliminate dengue transmission have little effect on endemic steady states or epidemic sizes. Unless control measures to reduce R ₀ by reducing mosquito populations are also put in place, it may be worth the extra effort in such cases to introduce Wolbachia strains that eliminate dengue transmission completely.

Appendix

The mosquito-only system is given by Eqs. (8) and (6), where all parameters are positive, u≤1, and v≤1. Letting x=n _m , y=n _w , the system becomes

$$ \begin{aligned} &\frac{dx}{dt} = \alpha g(x,y) f\bigl(g(x,y) + v \phi y \bigr) - x, \\ &\frac{dy}{dt} = \alpha v \phi y f\bigl(g(x,y) + v \phi y \bigr) - \delta y, \end{aligned} $$

(13)

where

$$ g(x,y) = \frac{(x + (1 - u)y)(x + (1 - v)\phi y)}{x + y}. $$

(14)

We shall analyse this system under the condition α>1, which is necessary and sufficient to ensure that there exists a Wolbachia-free steady state. On the x axis, which is invariant for the system, y=0 and g(x,y)=g(x,0)=x. The equation for x reduces to $\dot{x}=x(\alpha f(x)-1)$, with steady states x=0 and x=f ⁻¹(1/α)=1, unstable and stable respectively for the system restricted to the x axis. The full system therefore has steady states E ₀=(0,0) and E ₁=(1,0), where E ₀ is unstable and E ₁ has at least one stable eigenvalue (with eigenvector along the x axis). At any other steady state, we must have y≠0. Such steady states satisfy

$$ 0 = \alpha g(x,y) f\bigl(g(x,y) + v\phi y\bigr) - x,\qquad 0 = \alpha v \phi y f\bigl(g(x,y) + v\phi y\bigr) - \delta y, $$

(15)

so, since y≠0, αvϕf(g(x,y)+vϕy)=δ. If αvϕ≤δ, then this equation has no positive solution for z=g(x,y)+vϕy, since f(z)≤1 for z≥0. In fact, for this case, it follows directly from the comparison theorem on the second equation of (13) that the Wolbachia-infected mosquitoes cannot persist, and the solution of the system must tend to the steady state E ₁. Let us consider from now on the case αvϕ>δ. In this case, the properties of f ensure that the equation αvϕf(z)=δ has a unique positive solution for z=g(x,y)+vϕy, and we obtain

$$z = g(x,y) + v \phi y = f^{-1} \biggl(\frac{\delta}{\alpha v \phi} \biggr) = v \phi k, $$

say. Now substituting the value of f(z) into the first equation of (15) gives δg(x,y)=vϕx, and with (14) we have

$$x + \delta y = \delta k, $$

a straight line crossing the positive quadrant of the (x,y) plane. This must be solved with Eq. (14), which with δg(x,y)=vϕx may be written

$$v \phi x(x + y) = \delta\bigl(x + (1 - u)y\bigr) \bigl(x + (1 - v)\phi y\bigr), $$

or Ax ²+Bxy+Cy ²=0, where

$$A = v \phi - \delta, \qquad B = v \phi - \delta(1 - u) - \delta(1 - v)\phi, \qquad C = - \delta(1 - u) (1 - v)\phi. $$

This is a degenerate conic section in the (x,y) plane, whose solution set is the single point (0,0) if B ²<4AC, two straight lines through the origin if B ²>4AC, or a single straight line through the origin if B ²=4AC. In the case B ²>4AC, the two straight lines have gradients of opposite sign if AC<0, positive gradients if AC>0 and B>0, and negative gradients if AC>0 and B<0. If AC=0 then at least one of the straight lines is along an axis. Only straight lines with positive gradients (or along an axis) cut the line x+δy=k in the positive (or nonnegative) quadrant, and hence lead to a positive (or non-negative) steady state solution of the original equations. Note that C≤0 for relevant parameter values, and C<0 unless either u=1 or v=1 or both. From now on, we shall restrict ourselves to the realistic case that Wolbachia has fitness costs, fixing ϕ<1<δ, so that A=vϕ−δ<0 for any v≤1.

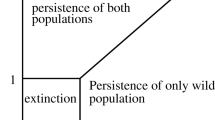
We wish to determine how the number of realistic steady states and their stability depends on the parameters u and v, in the relevant region S=[0,1]×[0,1] of (u,v) parameter space. Let us consider the case C=0 first, so that u=1 or v=1 or both. Then the solution set of the conic section consists of two straight lines, the y axis x=0 leading to a completely Wolbachia-infected steady state E ₂=(0,k), and the line Ax+By=0, leading to a positive steady state E ₃ with co-existence of Wolbachia-infected and Wolbachia-free mosquitoes if B>0, but to no realistic steady state if B<0. The straight line B=0 in (u,v) parameter space crosses the line v=1 at (u ₀,1), where u ₀=1−ϕ/δ, and the line u=1 at (1,v ₀), where v ₀=δ/(1+δ). Since B>0 at (u,v)=(1,1), there is a co-existence steady state as well as a completely Wolbachia-infected steady state at (1,1), for v ₀<v≤1 but not for 0≤v≤v ₀ if u=1, and for u ₀<u≤1 but not for 0≤u≤u ₀ if v=1, as shown in Fig. 5. At (u,v)=(1,1) the co-existence state E ₃ is determined by the intersection of the line x+δy=δk and the line Ax+By=(ϕ−δ)x+ϕy=0, and is therefore given by (x,y)=(x ^∗,y ^∗)=δk(ϕ,δ−ϕ)/(δ(δ−ϕ)+ϕ). Now let us consider the interior of the square S, where C<0. Near (1,1) then B ²>4AC and B>0, so that the solution set of the conic section consists of two straight lines with positive gradient, and there are two co-existence steady states E ₂ and E ₃. It is easy to show that the curve B ²=4AC touches but does not cross the line u=1 at v=v ₀, touches but does not cross the line v=1 at u=u ₀, and does not intersect the boundary of S anywhere else. The curve is sketched in Fig. 5. The co-existence steady states disappear through a saddle-node bifurcation as we move away from (1,1) and across the curve B ²=4AC, and although they reappear later if the curve is crossed again on the other side of the line B=0, they are no longer in the positive quadrant and are therefore unrealistic. Values of u and v given in the literature as u=1, v=1 (Hoffmann et al. 2011; Bian et al. 2010; McMeniman et al. 2009), where we have shown that there is a co-existence steady state as well as a completely Wolbachia-infected steady state, but a small deviation from these values leads to some Wolbachia-free mosquitoes in the previously completely Wolbachia-infected steady state.

Fig. 5

Steady states in (u,v) parameter space. Outside the closed curve B ²=4AC, (+,+) indicates that the solution set of the conic section Ax ²+Bxy+Cy ²=0 is made up of two straight lines with positive gradient, (+,0) (on u=1 or v=1) that one of the straight lines has positive gradient and the other is along the y axis, and similarly for (−,−) and (−,0). Straight lines with positive gradient correspond to co-existence steady states, those along the y axis to completely Wolbachia-infected steady states, while those with negative gradient do not correspond to steady states. Inside the closed curve B ²=4AC the solution set of the conic section is the point (x,y)=(0,0) only, which does not correspond to a steady state. Realistic values of (u,v) are close to (1,1), giving two steady states

To determine the stability of the steady states, we calculate the Jacobian matrix J, where

g and its derivatives are evaluated at (x,y), and f and f′ are evaluated at z=g(x,y)+vϕy. The derivatives of g are given by

At the Wolbachia-free steady state E ₁, at (x,y)=(1,0), we have g=1, g _x =1, g _y =(1−u)+(1−v)ϕ−1, z=1, f=1/α, and so

The eigenvalues are αf′(1)<0 and vϕ−δ, so E ₁=(1,0) is stable if vϕ<δ and unstable if vϕ>δ, stable for realistic parameter values. We shall initially determine the stability of the other steady states at parameter values (u,v)=(1,1). For the completely Wolbachia-infected steady state E ₂, at (x,y)=(0,k), g=g _x =g _y =0, z=αϕk, f=δ/(αϕ), and so

The eigenvalues are −1<0 and αϕ ² kf′<0, so E ₂=(0,k) is stable. At (u,v)=(1,1), and for realistic parameter values ϕ>δ, the steady state E ₃ is in the positive quadrant and is the only steady state in the positive quadrant. A straightforward but very tedious calculation then gives detJ<0 at E ₃, so that E ₃ is a saddle point, but a neater proof is as follows. Define the closed curve Γ to be the boundary of the region in (x,y) space defined in polar coordinates (r,θ) by 0<θ<π/2, 0<r<R, for R so large that dx/dt<0 and dy/dt<0 on r=R, perturbed into the positive quadrant to pass round the steady states E ₀, E ₁ and E ₂. It is clear that the Poincaré index of Γ is −1, so that E ₃ is a saddle point.

As we move in parameter space away from (u,v)=(1,1), then E ₂ enters the positive quadrant. As we arrive at and then cross the curve B ²=4AC it first coincides with E ₃ and then both disappear through a saddle–node bifurcation, leaving E ₁ as the globally stable steady state for non-zero initial conditions in the positive quadrant.