Confidence Distribution for the Ability Parameter of the Rasch Model

Abstract

In this paper, we consider the Rasch model and suggest novel point estimators and confidence intervals for the ability parameter. They are based on a proposed confidence distribution (CD) whose construction has required to overcome some difficulties essentially due to the discrete nature of the model. When the number of items is large, the computations due to the combinatorics involved become heavy, and thus, we provide first- and second-order approximations of the CD. Simulation studies show the good behavior of our estimators and intervals when compared with those obtained through other standard frequentist and weakly informative Bayesian procedures. Finally, using the expansion of the expected length of the suggested interval, we are able to identify reasonable values of the sample size which lead to a desired length of the interval.

Appendices

Appendix A

1.1 Proofs

Proof of Proposition 1

Consider first the case $s=1,\ldots ,n-1$. The density $h_{\,n,s}$ for $\theta$ is well defined and admits all moments if

$$\begin{aligned} I_{n,s}=\int _{-\infty }^{\infty }|\theta |^k \sqrt{h_{\,n,s}^r(\theta )h_{\,n,s}^{\ell }(\theta )}d\theta <\infty , \qquad k=0,1,\ldots . \end{aligned}$$

(A.1)

From the well-known fact that the geometric mean is not greater than the arithmetic mean, it follows that $I_{n,s}\le \int _{-\infty }^{\infty }|\theta |^k \frac{1}{2}(h_{\,n,s}^r(\theta )+h_{\,n,s}^{\ell }(\theta ))\, d\theta$, and thus, it is sufficient to show that there exists the k-th moment of $h_{\,n,s}^r$ and of $h_{\,n,s}^{\ell }$, $k=1,2,\ldots$. Now, using the density given in (7), we have

$$\begin{aligned} E(|\theta |^k)=\int _{-\infty }^{\infty }|\theta |^k \sum _{t=0}^{s} (n\bar{P}_n(\theta )-t)\exp \{\theta t - M_n(\theta )\} g_n(t) d\theta \end{aligned}$$

which is finite if for each $t=0,1, \ldots ,s$

$$\begin{aligned}&\int _{-\infty }^{\infty }|\theta |^k (n\bar{P}_n(\theta )-t)\exp \{\theta t - M_n(\theta )\} d\theta \nonumber \\&\quad = \int _{-\infty }^{\infty }|\theta |^k \left( \sum _{i=1}^{n} \frac{\exp \{\theta -b_i\}}{1+\exp \{\theta -b_i\}}-t\right) \frac{\exp \{\theta t\}}{\prod _{i=1}^n (1+\exp \{\theta -b_i\})} d\theta <\infty . \end{aligned}$$

(A.2)

Being the integrand in (A.2) asymptotic to $n|\theta |^k e^{\theta }$ when $t=0$ and to $-t|\theta |^k e^{\theta t}$ when $t=1,2,\ldots$ for $\theta \rightarrow -\infty$, and to $(n-t)|\theta |^k(1+e^{\theta })^{-(n-t)}$ for $\theta \rightarrow \infty$, the integral is finite and the result follows.

When $s=0$, the density of $h_{n,s}^\beta (\theta )$ and all the corresponding moments exist if $\int _{-\infty }^{\infty }|\theta |^k h_{n,s}^\beta (\theta ) d\theta$ is finite for $k=0,1,\ldots$. Using (7), we have to show that

$$\begin{aligned}&\int _{-\infty }^{\infty }|\theta |^k [n\bar{P}_n(\theta )\exp \{- M_n(\theta )\}]^\beta d\theta \\&\quad = \int _{-\infty }^{\infty }|\theta |^k \left( \sum _{i=1}^{n} \frac{\exp \{\theta -b_i\}}{1+\exp \{\theta -b_i\}}\right) ^\beta \left( \frac{1}{\prod _{i=1}^n (1+\exp \{\theta -b_i\})}\right) ^\beta d\theta <\infty . \end{aligned}$$

Because the integrand is asymptotic to $|\theta |^k n^\beta e^{\theta \beta }$ for $\theta \rightarrow -\infty$, and to $|\theta |^k ne^{-n\theta \beta }$ for $\theta \rightarrow \infty$, the result follows recalling that $\beta \in (0,1]$. The proof is similar for the case $s=n$, observing that $h_{n,n}^\beta (\theta )=(n-\bar{P}_n(\theta ))\exp \{\theta n - M_n(\theta )\}$. $\square$

Proof of Theorem 1

Let $\theta _0$ be the true value of the parameter $\theta$, and let $P_0(\theta _0)=\exp \{\theta _0-b_0\}/(1+\exp \{\theta _0-b_0\})$. Thus, from the Cesàro mean theorem, $\bar{P}_n(\theta _0)= \sum _{i=1}^n P_i(\theta _0)/n \rightarrow P_0(\theta _0)$, ($n\rightarrow \infty$). From (6), we have $E_{\theta }(\bar{X}_n)=\bar{P}_n(\theta )$, and because

$$\begin{aligned} \lim _{n \rightarrow \infty } \sum _{i=1}^n \frac{1}{i^2} Var_{\theta }(X_i)= \lim _{n \rightarrow \infty } \sum _{i=1}^n \frac{1}{i^2} \frac{\exp \{\theta -b_i\}}{(1+\exp \{\theta -b_i\})^2} \le \lim _{n \rightarrow \infty } \sum _{i=1}^n \frac{1}{i^2}=\frac{\pi ^2}{6} < \infty , \end{aligned}$$

the strong law of large numbers holds, i.e., $\bar{X}_n{\mathop {\rightarrow }\limits ^{a.s.}}P_0(\theta _0)$, see Serfling (1980, Sect. 1.8). In conclusion, $\bar{x}_n$ converges to $P_0(\theta _0)$ for almost all sequences $(x_1, x_2, \ldots )$.

Now, $Var_{\theta }(S_n)=\sum _{i=1}^n \exp \{\theta -b_i\}/(1+\exp \{\theta -b_i\})^2 \rightarrow \infty$, for $n\rightarrow \infty$, because the general term of the series does not tend to 0, and thus, from Deheuvels et al. (1989, Theorem 1.1) we have

$$\begin{aligned} \frac{\sqrt{n}(\bar{X}_n-\bar{P}_n(\theta ))}{\bar{P}^{\prime }_n(\theta )^{1/2}} \rightarrow N(0,1), \quad n\rightarrow \infty . \end{aligned}$$

(A.3)

If $\theta$ is distributed according to the CD defined in (2), we can write

$$\begin{aligned} \text{ Pr}_{\bar{x}_n}\left\{ \sqrt{n}(\theta -\hat{\theta })\le z \right\} =\text{ Pr}_{\bar{x}_n}\{\theta \le \theta _n\}= 1- \text{ Pr}_{\theta _n}\{\bar{X}_n^* \le \bar{x}_n\}, \end{aligned}$$

(A.4)

where $\theta _n=\hat{\theta }+z/\sqrt{n}$ and $\bar{X}^*_n$ is the sample mean of n independent Bernoulli random variables with success probability $P_i(\theta _n)$, $i=1, \ldots ,n$. Notice that, for $z \in \mathbb {R}$, $\theta _n$ belongs to the natural parameter space because $\Theta =\mathbb {R}$ and $\theta _n$ converges to $\theta _0$. The latter fact follows from the convergence of the sample mean stated above and the relationship between the natural and the mean parameter of a NEF.

Using (A.3), we can write, for each $\epsilon >0$ and n large enough,

$$\begin{aligned} \left| \text{ Pr}_{\theta _n}\{\bar{X}_n^* \le \bar{x}_n\}-\Phi \left( \frac{\sqrt{n}(\bar{x}_n-\bar{P}_n(\theta _n))}{\bar{P}^{\prime }_n(\theta _n)^{1/2}}\right) \right| < \epsilon \quad a.s.\; P_{\theta _0}. \end{aligned}$$

(A.5)

The term $(\bar{x}_n-\bar{P}_n(\theta _n))\bar{P}^{\prime }_n(\theta _n)^{-1/2}$, appearing in (A.5), admits a standard Taylor expansion because it is equidifferentiable thanks to the assumption of boundedness of the sequence of the $b_i$’s. Recalling that $\bar{P}_n(\hat{\theta })=\bar{x}_n$, we have

$$\begin{aligned} \frac{\bar{x}_n-\bar{P}_n(\theta _n)}{\bar{P}^{\prime }_n(\theta _n)^{1/2}}= & {} \frac{\bar{x}_n-\bar{P}_n(\hat{\theta })}{\bar{P}^{\prime }_n(\hat{\theta })^{1/2}}+z/\sqrt{n} \left( -\bar{P}^{\prime }_n(\hat{\theta })^{1/2}-\frac{\bar{P}^{\prime \prime }_n(\hat{\theta })(\bar{x}_n-\bar{P}_n(\hat{\theta }))}{ 2\bar{P}^{\prime }_n(\hat{\theta })^{3/2}}\right) +O(n^{-1}) \nonumber \\= & {} -z\sqrt{\bar{P}^{\prime }_n(\hat{\theta })/n} +O(n^{-1}) . \end{aligned}$$

(A.6)

Thus, (A.5) can be written as

$$\begin{aligned}&\left| \text{ Pr}_{\theta _n}\{\bar{X}_n^* \le \bar{x}_n\}-\Phi \left( -z\sqrt{\bar{P}^{\prime }_n(\hat{\theta })} \right) \right| = \left| 1-\text{ Pr}_{\theta _n}\{\bar{X}_n^* \le \bar{x}_n\}- \left( 1 -\Phi \left( -z \sqrt{\bar{P}^{\prime }_n(\hat{\theta })} \right) \right) \right| \\&\quad = \left| \text{ Pr}_{\bar{x}_n} \left\{ \sqrt{n}(\theta -\hat{\theta })\le z \right\} -\Phi \left( z \sqrt{\bar{P}^{\prime }_n(\hat{\theta })} \right) \right| < \epsilon \quad a.s. \; P_{\theta _0}, \end{aligned}$$

where the last equality follows from (A.4). As a consequence, the convergence stated in Theorem 1 is proved for $\theta$ distributed according to $H^r_{n,s}(\theta )$.

Because $H^{\ell }_{n,s}(\theta )=H^r_{n,s-1}(\theta )$, the previous result holds also for $H^{\ell }_{n,s}(\theta )$ provided the following conditions for the asymptotic normality are satisfied (see Serfling 1980, Sect. 1.5.5),

$$\begin{aligned} \sqrt{\frac{n\bar{P}^{\prime }_n(\hat{\theta })}{n\bar{P}^{\prime }_n(\hat{\theta }^-)}}= & {} \sqrt{\frac{\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}))}{\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}-1/n))}} \rightarrow 1, \quad n\rightarrow \infty \\ \sqrt{n\bar{P}^{\prime }_n(\hat{\theta })}(\hat{\theta }-\hat{\theta }^{-})= & {} \sqrt{n\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}))}(\bar{P}_n^{-1}(\bar{x})-\bar{P}_n^{-1}(\bar{x}-1/n)) \rightarrow 0, \quad n\rightarrow \infty , \end{aligned}$$

where ${\hat{\theta }}^{-}$ is the MLE corresponding to the score $s - 1$. The first condition is true because all functions involved are continuous and admit finite limits, while the second holds because

$$\begin{aligned} \bar{P}_n^{-1}(\bar{x})-\bar{P}_n^{-1}(\bar{x}-1/n)=- \frac{1}{n} \frac{1}{\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}))} +O(n^{-1}). \end{aligned}$$

Finally, the result for $H_{n,s}(\theta )$ follows from (3). $\square$

The following proposition details the smoothing effect of the geometric mean on the asymptotic CD, described before Theorem 2, when observations are lattice random variables.

Proposition 2 Assume that the distribution functions $\tilde{H}_{n,s}^r$ and $\tilde{H}_{n,s}^{\ell }$ of $\sqrt{n}(\theta -\hat{\theta })$ with $\theta$ distributed according to $H_{n,s}^r$ and $H_{n,s}^{\ell }$, respectively, have the following Edgeworth expansion

$$\begin{aligned} \tilde{H}_{n,s}^\delta (z)=\Phi (z/\hat{\sigma })-\phi (z/\hat{\sigma })\left[ A(z)+\gamma _d\frac{k\hat{\sigma }}{2}\right] \frac{1}{\sqrt{n}}+ O(n^{-1}), \end{aligned}$$

(A.7)

where $d \in \{r,\ell \}$, $\gamma _r=1$, $\gamma _{\ell }=-1$ and A(z) is a polynomial of second degree in z. Then, the expansion of $\tilde{H}_{n,s}$ is

$$\begin{aligned} \tilde{H}_{n,s}(z)=\Phi (z/\hat{\sigma })-\phi (z/\hat{\sigma })A(z)\frac{1}{\sqrt{n}}+ O(n^{-1}) \end{aligned}$$

(A.8)

and thus do not depend on the term $\gamma _d k \hat{\sigma }/2$.

Proof of Proposition 2

Recalling that $H_{n,s}$ is the distribution function of $\theta$ corresponding to the (normalized) geometric mean $h_{\,n,s}$ of the densities $h_{\,n,s}^r$ and $h_{\,n,s}^{\ell }$, it follows that the density of a linear transformation of type $T=a\theta +b$, for constants $a\ne 0$ and b, can be obtained as the (normalized) geometric mean of $h_{\,n,s}^r((t-b)/a)|1/a|)$ and $h_{\,n,s}^\ell ((t-b)/a)|1/a|)$. Using (A.7), the expansion of the density $\tilde{h}_{n,s}^d(z)$ is given by

$$\begin{aligned} \tilde{h}_{n,s}^d(z)=\phi (z/\hat{\sigma })\frac{1}{\hat{\sigma }}-\left\{ \phi ^{\prime } (z/\hat{\sigma })\frac{1}{\hat{\sigma }} \left[ A(z)+\gamma _d\frac{k\hat{\sigma }}{2}\right] + \phi (z/\hat{\sigma }) A^{\prime }(z)\right\} \frac{1}{\sqrt{n}}+ O(n^{-1}), \end{aligned}$$

where for a function f, as usual, $f^\prime$ denotes its derivative.

Because $\tilde{h}_{n,s}(z)=k_n^{-1}\sqrt{\tilde{h}_{n,s}^r(z) \tilde{h}_{n,s}^\ell (z)}$, where $k_n=\int \sqrt{\tilde{h}^r_{n,s} (z) \tilde{h}_{n,s}^\ell (z)} dz$, from

$$\begin{aligned} \tilde{h}^r_{n,s}(z) \tilde{h}_{n,s}^\ell (z) = \phi ^2(z/\hat{\sigma })\frac{1}{\hat{\sigma }^2} - 2\phi (z/\hat{\sigma })\frac{1}{\hat{\sigma }} \left[ \phi ^{\prime }(z/\hat{\sigma })\frac{1}{\hat{\sigma }}A(z)+\phi (z/\hat{\sigma })A^{\prime }(z) \right] n^{-1/2}+ O(n^{-1}), \end{aligned}$$

we obtain

$$\begin{aligned} \sqrt{\tilde{h}^r_{n,s}(z) \tilde{h}_{n,s}^\ell (z)} =\phi (z/\hat{\sigma })\frac{1}{\hat{\sigma }} - \left[ \phi ^{\prime }(z/\hat{\sigma })\frac{1}{\hat{\sigma }}A(z)+\phi (z/\hat{\sigma })A^{\prime }(z) \right] n^{-1/2} + O(n^{-1}). \end{aligned}$$

(A.9)

We now derive the expansion of $k_n$ by integrating (A.9). Using standard properties of the normal density and recalling that A(z) is a polynomial of second degree in z, we have

$$\begin{aligned} k_n= & {} \int _{-\infty }^{+\infty } (\phi (z/\hat{\sigma })\frac{1}{\hat{\sigma }} - \left[ \phi ^{\prime }(z/\hat{\sigma })\frac{1}{\hat{\sigma }}A(z)+\phi (z/\hat{\sigma })A^{\prime }(z) \right] n^{-1/2} + O(n^{-1})\\= & {} 1- \phi (z/\hat{\sigma })A(z) |_{-\infty }^{+\infty } +O(n^{-1})= 1+O(n^{-1}). \end{aligned}$$

As a consequence, the expansion of $\tilde{h}_{n,s}(z)$ coincides with that given in (A.9). Finally, from the expansion of the density given in (A.9) we derive the expansion (A.8) of the corresponding CD through a term by term integration. $\square$

The previous proposition is crucial for the following proof.

Proof of Theorem 2

Consider first the distribution function $\tilde{H}_{n,s}^r$ of $\sqrt{n}(\theta -\hat{\theta })$ with $\theta$ distributed according to $H_{n,s}^r$. Following the proof of Theorem 1, we can write, using (A.4) and the fact that $\bar{x}_n=\bar{P}_n(\hat{\theta })$, with $\bar{P}_n(\theta )$ increasing in $\theta$,

$$\begin{aligned} \tilde{H}_{n,s}^r(z)= & {} \text{ Pr}_{\bar{x}_n}\left\{ \sqrt{n}(\theta -\hat{\theta })\le z \right\} = 1- \text{ Pr}_{\theta _n}\{\bar{X}_n^* \le \bar{x}_n\} \nonumber \\= & {} 1- \text{ Pr}_{\theta _n}\left\{ \frac{\sqrt{n}(\bar{X}_n^*-\bar{P}_n(\theta _n))}{{\mathop {\bar{P}^{\prime }_n(\theta _n)^{1/2}}\limits ^{}}} \le \frac{\sqrt{n}(\bar{P}_n(\hat{\theta })-\bar{P}_n(\theta _n))}{{\bar{P}^{\prime }_n(\theta _n)^{1/2}}}\right\} \nonumber \\= & {} 1-\tilde{F}_n \left( \frac{\sqrt{n}(\bar{P}_n(\hat{\theta })-\bar{P}_n(\theta _n))}{{{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{1/2}}}\right) , \end{aligned}$$

(A.10)

where $\tilde{F_n}$ is implicitly defined in (A.10).

Notice that $\{X^*_{nj}, \, 1 \le j \le n\}$ is a triangular array of random variables such that: a) for all $n\ge 1$, $X^*_{n1}, \dots , X^*_{nn}$ are independent and b) for all $j\in \{1,2,\ldots , n\}$, $X^*_{nj}$ follows a Bernoulli distribution with success probability $P_j(\theta _n)$, so that the expansion of

$$\begin{aligned} \tilde{F}_n(t)=\text{ Pr}_{\theta _n}\left\{ \frac{\sqrt{n}(\bar{X}_n^*-\bar{P}_n(\theta _n))}{{{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{1/2}}}\le t\right\} \end{aligned}$$

can be derived using the result in Deheuvels et al. (1989, Theorem 1.3). Specifically, they consider a smooth version $\breve{F}_n$ of $\tilde{F}_n$, which in our context is given by

• (i) $\breve{F}_{n}(t_{nk})=\tilde{F}_n(t_{nk})$ for $t_{nk}=(k-n\bar{P}_n(\theta _n)+1/2)/(\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2})$, $k=0,\pm 1,\pm 2\ldots$;

• (ii) $\breve{F}_{n}(t)$ is continuous in t, and linear on all intervals $(t_{n(k-1)},t_{nk})$, $k=0,\pm 1,\pm 2\ldots$.

The expansion of $\breve{F}_n$ is

$$\begin{aligned} \breve{F}_n(t)=\Phi (t) +\phi (t)\frac{1}{6}\frac{\bar{P}^{\prime \prime }_n(\theta _n)}{{{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{3/2}}}(1-t^2)\frac{1}{\sqrt{n}}+ O(n^{-1}). \end{aligned}$$

(A.11)

If t is an observed point, i.e., $t=(s-n\bar{P}_n(\theta _n))/(\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2})$, using the previous condition (i) and (A.11), we have

$$\begin{aligned} \tilde{F}_n(t)= & {} \tilde{F}_n\left( t+\frac{1}{2\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2}}\right) = \breve{F}_n\left( t+\frac{1}{2\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2}}\right) = \Phi \left( t+\frac{1}{2\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2}}\right) \\&+\phi \left( t+\frac{1}{2\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2}}\right) \frac{1}{6}\frac{\bar{P}^{\prime \prime }_n(\theta _n)}{{{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{3/2}}} \left( 1-\left( t+\frac{1}{2\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2}}\right) ^2\right) \frac{1}{\sqrt{n}}+ O(n^{-1}). \end{aligned}$$

A further expansion in t of the last expression gives

$$\begin{aligned} \tilde{F}_n(t)=\Phi (t) +\phi (t)\left[ \frac{1}{6}\frac{\bar{P}^{\prime \prime }_n(\theta _n)}{{{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{3/2}}}(1-t^2)+\frac{1}{2{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{1/2}}\right] \frac{1}{\sqrt{n}} + O(n^{-1}), \end{aligned}$$

(A.12)

which depends only on the Taylor expansion of $\Phi (t+1/(2\sqrt{n}\bar{P}^{\prime }_n(\theta _n)^{1/2}))$ appearing in $\tilde{F}_n(t)$, because the higher-order terms of the expansions of the other components of $\tilde{F}_n(t)$ are absorbed in $O(n^{-1})$. Note that the extra term characterizing the Edgeworth expansion of a lattice random variables appears in (A.12).

Recalling the expression of t and that $s=n\bar{x}=n\bar{P}_n(\hat{\theta })$, from (A.10) we have

$$\begin{aligned} \tilde{H}_{n,s}^r(z)=1-\tilde{F}_n(t)=\Phi (-t) -\phi (t)\left[ \frac{1}{6}\frac{\bar{P}^{\prime \prime }_n(\theta _n)}{{{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{3/2}}}(1-t^2)+\frac{1}{2{\mathop {\bar{P}^{\prime }_n}\limits ^{}}(\theta _n)^{1/2}}\right] \frac{1}{\sqrt{n}}+ O(n^{-1}). \end{aligned}$$

Now, using (A.6), it is possible to show that the expansions of $\Phi (-t)$, $\phi (t)$ and $t^2$ are $\Phi (z\bar{P}^{\prime }_n(\hat{\theta })^{1/2})+ O(n^{-1})$, $\phi (z\bar{P}^{\prime }_n(\hat{\theta })^{1/2})+ O(n^{-1})$ and $z^2\bar{P}^{\prime }_n(\hat{\theta })+ O(n^{-1})$, respectively. Thus,

$$\begin{aligned} \tilde{H}_{n,s}^r (z)= & {} \Phi \left( z\bar{P}^{\prime }_n(\hat{\theta })^{1/2}\right) -\phi \left( z\bar{P}^{\prime }_n(\hat{\theta })^{1/2}\right) \left[ \frac{1}{6} \frac{\bar{P}^{\prime \prime }_n(\hat{\theta })}{\bar{P}^{\prime }_n(\hat{\theta })^{3/2}}\left( 1-z^2\bar{P}^{\prime }_n(\hat{\theta })\right) +\frac{1}{2\bar{P}^{\prime }_n(\hat{\theta })^{1/2}}\right] \frac{1}{\sqrt{n}}\nonumber \\&+ O(n^{-1}). \end{aligned}$$

(A.13)

Consider now $H^{\ell }_{n,s}$ and recall that $H^{\ell }_{n,s}(\theta )=H^r_{n,s-1}(\theta )$. Thus, the expansion of the CD for $\sqrt{n}(\theta -\hat{\theta }^-)$, where $\hat{\theta }^-=\bar{P}_n^{-1}(\bar{x}_n-1/n)$, can be obtained directly from (A.13). To obtain the expansion of $\sqrt{n}(\theta -\hat{\theta })$ (with $\theta$ distributed according to $H^{\ell }_{n,s}(\theta )$, we can write

$$\begin{aligned}&\text{ Pr}_{s-1}\left\{ \sqrt{n}(\theta -\hat{\theta })\le z \right\} = \text{ Pr}_{s-1}\left\{ \sqrt{n}(\theta -\hat{\theta }^-)\le z+\sqrt{n}(\hat{\theta }-\hat{\theta }^-) \right\} \qquad \nonumber \\&\quad = \Phi \left( [z+\sqrt{n}(\hat{\theta }-\hat{\theta }^-)]\bar{P}^{\prime }_n(\hat{\theta }^-)^{1/2}\right) -\phi \left( [z+\sqrt{n}(\hat{\theta }-\hat{\theta }^-)]\bar{P}^{\prime }_n(\hat{\theta }^-)^{1/2}\right) \qquad \nonumber \\&\qquad \left[ \frac{1}{6}\frac{\bar{P}^{\prime \prime }_n(\hat{\theta })}{\bar{P}^{\prime }_n(\hat{\theta })^{3/2}}\left( 1-[z+\sqrt{n}(\hat{\theta }-\hat{\theta }^-)]^2\bar{P}^{\prime }_n(\hat{\theta }^-)\right) +\frac{1}{2\bar{P}^{\prime }_n(\hat{\theta })^{1/2}}\right] \frac{1}{\sqrt{n}}+O(n^{-1}).\qquad \end{aligned}$$

(A.14)

Observe that the argument of $\Phi$ and $\phi$

$$\begin{aligned} {[}z+\sqrt{n}(\hat{\theta }-\hat{\theta }^-)]\bar{P}^{\prime }_n(\hat{\theta }^-)^{1/2}= [z+\sqrt{n}(\bar{P}_n^{-1}(\bar{x}_n) -\bar{P}_n^{-1}(\bar{x}_n-1/n))]\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}_n-1/n))^{1/2}, \end{aligned}$$

can be seen as a function g of $\bar{x}_n-1/n$ whose Taylor expansion in the point $\bar{x}_n$ is

$$\begin{aligned} g(\bar{x}_n-1/n)= & {} z\sqrt{\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}_n))}+\frac{1}{\sqrt{\bar{P}^{\prime }_n(\bar{P}_n^{-1}(\bar{x}_n))}}\frac{1}{\sqrt{n}}+O(n^{-1}) \nonumber \\= & {} z\sqrt{\bar{P}^{\prime }_n(\hat{\theta })}+\frac{1}{\sqrt{\bar{P}^{\prime }_n(\hat{\theta })}}\frac{1}{\sqrt{n}}+O(n^{-1}). \end{aligned}$$

(A.15)

As a consequence, we have

$$\begin{aligned} \Phi (g(\bar{x}_n-1/n))= & {} \Phi (z\bar{P}^{\prime }_n(\hat{\theta })^{1/2})+\phi (z\bar{P}^{\prime }_n(\hat{\theta })^{1/2}) \frac{1}{\bar{P}^{\prime }_n(\hat{\theta })^{1/2}}\frac{1}{\sqrt{n}}+O(n^{-1}) \end{aligned}$$

(A.16)

$$\begin{aligned} \phi (g(\bar{x}_n-1/n))= & {} \phi ((z\bar{P}^{\prime }_n(\hat{\theta })^{1/2})+O(n^{-1/2}) . \end{aligned}$$

(A.17)

Finally, substituting (A.16) and (A.17) into (A.14), we obtain

$$\begin{aligned} \tilde{H}_{n,s}^{\ell }(z)= & {} \Phi (z\bar{P}^{\prime }_n(\hat{\theta })^{1/2}) -\phi (z\bar{P}^{\prime }_n(\hat{\theta })^{1/2}) \nonumber \\&\left[ \frac{1}{6}\frac{\bar{P}^{\prime \prime }_n(\hat{\theta })}{\bar{P}^{\prime }_n(\hat{\theta })^{3/2}}\left( 1-z^2\bar{P}^{\prime }_n(\hat{\theta })\right) -\frac{1}{2\bar{P}^{\prime }_n(\hat{\theta })^{1/2}}\right] \frac{1}{\sqrt{n}}+O(n^{-1}). \end{aligned}$$

(A.18)

Applying Proposition 2 to (A.13) and (A.18), the result follows. $\square$

Proof of Theorem 3

First, we provide a stochastic expansion of the MLE $\hat{\theta }$. Notice that the log likelihood of the Rasch model

$$\begin{aligned} \ell (\theta )=\theta s -\sum _{i=1}^n \log (1+\exp \{\theta -b_i\}) \end{aligned}$$

(A.19)

satisfies the regularity conditions assumed by Severini (2000, Sect. 3.4), as can be seen arguing as in his Example 3.8. Furthermore, from the expression (A.19), it is immediate to conclude that the derivatives from the second-order onwards of $\ell (\theta )$, with respect to $\theta$, do not depend on s, so that all the standardized log-likelihood derivatives are equal to 0 with the exception of $Z_1=(\ell _\theta (\theta )- E_\theta (\ell _\theta (\theta )))/\sqrt{n}=\ell _\theta (\theta )/\sqrt{n}$, where $\ell _\theta (\theta )$ denotes the first derivative of $\ell (\theta )$. As a consequence, the stochastic expansion of the MLE $\hat{\theta }$, obtained using formula (5.7) in Severini (2000), is

$$\begin{aligned} \hat{\theta }= & {} \theta +\dfrac{Z_1}{\bar{P}^{\prime }_n(\theta )}\,n^{-1/2} - \frac{1}{2}\frac{\bar{P}^{\prime \prime }_n(\theta )}{\bar{P}^{\prime }_n(\theta )^3}Z_1^2 n^{-1} + \left( \frac{1}{6}\frac{(-\bar{P}^{\prime \prime \prime }_n(\theta ))}{\bar{P}^{\prime }_n(\theta )^4}-\frac{1}{2} \frac{\bar{P}^{\prime \prime }_n(\theta )^2}{(-\bar{P}^{\prime }_n(\theta ))^5)}\right) Z_1^3\,n^{-3/2} \nonumber \\&+ O_p(n^{-2}). \end{aligned}$$

(A.20)

To provide an expansion of

$$\begin{aligned} E(L_n(\hat{\theta },z_{1-\alpha /2}))=2z_{1-\alpha /2\,} E_\theta (\bar{P}^{\prime }_n(\hat{\theta })^{-1/2})\,n^{-1/2}, \end{aligned}$$

(A.21)

we first develop a Taylor expansion of $h(\hat{\theta })=\bar{P}^{\prime }_n(\hat{\theta })^{-1/2}$ in $\hat{\theta }=\theta$, where the increment $\hat{\theta }-\theta$ is derived from (A.20), and then, we compute the expectation with respect to $Z_1$. More formally, because $E_\theta (Z_1)=0$ and $E_\theta (Z_1^2)=\bar{P}^{\prime }_n(\theta )$, we have

$$\begin{aligned} E_\theta (\hat{\theta }-\theta )= -\frac{1}{2}\frac{\bar{P}^{\prime \prime }_n(\theta )}{\bar{P}^{\prime }_n(\theta )^2}n^{-1} +O(n^{-3/2}) \quad \text{ and }\quad E_\theta (\hat{\theta }-\theta )^2= \frac{1}{\bar{P}^{\prime }_n(\theta )}n^{-1}+O(n^{-3/2}) \end{aligned}$$

so that

$$\begin{aligned} E_\theta (h(\hat{\theta }))= & {} h(\theta )+h^{\prime }(\theta )E_\theta (\hat{\theta }-\theta )+\frac{1}{2}h^{\prime \prime }(\theta )E_\theta ((\hat{\theta }-\theta )^2)+O(n^{-3/2}) \nonumber \\= & {} \bar{P}^{\prime }_n(\theta )^{-1/2}+ \left( \frac{5}{8}\,\frac{\bar{P}^{\prime \prime }_n(\theta )^2}{\bar{P}^{\prime }_n(\theta )^{7/2}}-\frac{1}{4}\,\frac{\bar{P}^{\prime \prime \prime }_n(\theta )}{\bar{P}^{\prime }_n(\theta ) ^{5/2}}\right) n^{-1}+O(n^{-3/2}) . \end{aligned}$$

(A.22)

Finally, substituting (A.22) in (A.21), the result given in (14) follows. $\square$

Appendix B

1.1 Further Figures for Example 1 ctd and Example 2

Fig. 8

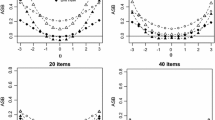
Example 1 ctd. Coverage (left) and expected length (right) of $I_{CD}$ (solid black) and $I_{WLE}$ (dashed blue), for $\alpha =0.2$ (first row) and $\alpha =0.05$ (second row).

Fig. 9

Example 2. First row: bias and MSE of CD-median (solid black), MLE (dashed blue) and WLE (dotted green), for $\theta \in (-4,6)$. Second row: coverage and expected length of $I_{CD}$ (solid black), $I_W$ (dashed blue) and $I_{WLE}$ (dotted green), for $\alpha =0.05$.