Optimal Energy to Spectral-Efficiency Trade-off in Cooperative Networks

Abstract

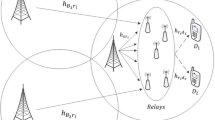
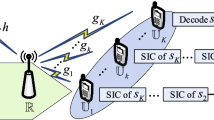
In this paper, the relationship between the energy efficiency in terms of the total consumed power per bit and the spectral efficiency is studied for dual-hop cooperative relaying systems consisting of multiple single-antenna amplify-and-forward relays. Considering the source and relay transmit antenna gains, the path-loss fading and the power consumption model as a whole, a new metric to measure the energy to spectral-efficiency trade-off (ESET) is formulated. Based on the convexity analysis of the new cost function, an analytical expression of the minimum per-bit power consumed by the whole relay system is derived as a general framework of the best ESET for given number of relays and relay-to-source power allocation. The relay-to-source power ratio is then further optimized, leading to a closed-form solution to relay design and power allocation. Numerical simulation results validating the theoretical analysis and the derived optimal ESET are provided.

Appendix : Convexity discussions of f w.r.t. R for Case iii: \(b<0<a\).

In this case, the following inequality always holds $1-\frac{b}{a}>1$. Then, the second-order derivative of the energy efficiency w.r.t. the spectral efficiency could be either positive or negative as shown in (15). Specifically, $f$ is convex w.r.t. $R$ when

$$\begin{aligned} q>\frac{2}{\left( {\ln 2} \right) ^{2}}\left( {1-\frac{b}{a}} \right) , \end{aligned}$$

(33)

otherwise when

$$\begin{aligned} q\le \frac{2}{\left( {\ln 2} \right) ^{2}}\left( {1-\frac{b}{a}} \right) \end{aligned}$$

(34)

$f$ is concave w.r.t. to $R$, where $q$ is given by (18) and is exclusively determined by the spectral efficiency $R$. Thus, it is essential to find the region of $R$ which makes (33) hold for the convexity of $f$ as well as the region which makes (34) hold for the concavity of $f$.

By observing (18), it is found that $q$ is an increasing function of $R$ in the whole region. Thus, there exists one and only one solution to the following equation

$$\begin{aligned} q=2^{R}\left\{ {\left( {R-\frac{1}{\ln 2}} \right) ^{2}+\frac{1}{\left( {\ln 2} \right) ^{2}}} \right\} =\frac{2}{\left( {\ln 2} \right) ^{2}}\left( {1-\frac{b}{a}} \right) \end{aligned}$$

(35)

for $R$ that determines (33) and (34). Let us denote this solution as $R_0$. Then, (33) is valid in the region of

$$\begin{aligned} R\ge R_0 , \end{aligned}$$

(36)

whereas (34) is valid in the region of $R$

$$\begin{aligned} 0<R<R_0 . \end{aligned}$$

(37)

To determine the value of $R_0$, we need to solve equation (35) for $R$. However, (35) is in the form of the generalized Lambert function [35] and it is not possible to obtain its exact mathematical solution. Therefore, we resort to an approximation of (35).

Through numerical simulations as shown in Fig. 2, it is found that the value of $q$ in (35) as a function of $R$ can be precisely approximated by $q{\prime }=2^{R}\left( {R-\frac{1}{\ln 2}} \right) ^{2}$, namely,

$$\begin{aligned} q\approx 2^{R}\left( {R-\frac{1}{\ln 2}} \right) ^{2}. \end{aligned}$$

(38)

Substituting (38) into (35), we get

$$\begin{aligned} 2^{R}\left( {R-\frac{1}{\ln 2}} \right) ^{2}=\frac{2}{\left( {\ln 2} \right) ^{2}}\left( {1-\frac{b}{a}} \right) . \end{aligned}$$

(39)

The exact solution to (39) can then be determined as follows. As shown in Fig. 2, it is seen that the approximation from (38) is very tight to the exact function in every regime of the spectral efficiency.

Multiplying both sides of (39) with $2^{R}$ gives

$$\begin{aligned} \left( {R-\frac{1}{\ln 2}} \right) ^{2}=\frac{2}{\left( {\ln 2} \right) ^{2}}\left( {1-\frac{b}{a}} \right) 2^{-R}. \end{aligned}$$

(40)

Computing the square root on both sides of (40) and then multiplying both sides with $2^{\frac{1}{2\ln 2}}$, we have

$$\begin{aligned} 2^{\frac{1}{2\ln 2}}\left( {R-\frac{1}{\ln 2}} \right) =\frac{1}{\ln 2}\sqrt{\frac{2\left( {a-b} \right) }{a}}2^{-\frac{1}{2}\left( {R-\frac{1}{\ln 2}} \right) }e^{jl\pi }, \quad \left( {l=0,\,1} \right) . \end{aligned}$$

(41)

Noting that $2^{-\frac{1}{2}\left( {R-\frac{1}{\ln 2}} \right) }=\exp \left\{ {-\frac{1}{2}\left( {R-\frac{1}{\ln 2}} \right) \ln 2} \right\}$, (41) can be further rewritten as

$$\begin{aligned} e^{\frac{\ln 2}{2}\left( {R-\frac{1}{\ln 2}} \right) }\left\{ {\frac{\ln 2}{2}\left( {R-\frac{1}{\ln 2}} \right) } \right\} =\frac{1}{2}\sqrt{\frac{2\left( {a-b} \right) }{a}}2^{-\frac{1}{2\ln 2}}e^{jl\pi }. \end{aligned}$$

(42)

The solution to the above equation can be obtained by using the standard Lambert function, which is expressed as the inverse function of $x=\mathbb {W}\left\{ {xe^{x}} \right\}$. Thus, the solution to (39) is given by

$$\begin{aligned} R_l =\frac{1}{\ln 2}+\frac{2}{\ln 2}\mathbb {W}\left\{ {\frac{1}{2}\sqrt{\frac{2\left( {a-b} \right) }{a}}2^{-\frac{1}{2\ln 2}}e^{jl\pi }} \right\} , \quad \left( {l=0,\hbox { 1}} \right) . \end{aligned}$$

(43)

The above solution identifies different regions of the spectral efficiency $R$ for the convexity and concavity of $f$. It is noticed that (43) gives two solutions because of the approximation of $q$ in (38). In fact, only one solution is valid considering that $q$ is an increasing function of $R$, as verified by numerical simulations shown in Fig. 2. Therefore, we choose the larger one from (43) corresponding to $l=0$ as the solution to (35),

$$\begin{aligned} R_0 =\frac{1}{\ln 2}+\frac{2}{\ln 2}\mathbb {W}\left\{ {\frac{1}{2}\sqrt{\frac{2\left( {a-b} \right) }{a}}2^{-\frac{1}{2\ln 2}}} \right\} =\log _2 e+2\left( {\log _2 e} \right) \mathbb {W}\left\{ {\frac{1}{2}\sqrt{\frac{2\left( {a-b} \right) }{ea}}} \right\} . \end{aligned}$$

(44)

Recalling (36) and (37), the region of $R$ for the convexity of $f$ and that for its concavity have been identified by (44). It is noted that the value of $R_0$ is very small, almost in the range of $\left[ {0,1} \right]$. Thus, the energy efficiency function is nearly convex w.r.t. the spectral efficiency $R$ in Case 3: $b<0<a$. End of proof.