Transient Heat Conduction Between Rough Sliding Surfaces

Abstract

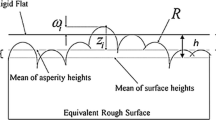
When two rough bodies slide against each other, asperities on the opposing surfaces interact with each other, defining a transient contact and heat conduction problem. We represent each body by a Greenwood and Williamson asperity model with a Gaussian height distribution of identical spherical asperities. The heat transfer during a typical asperity interaction is analyzed, and the results are combined with the height distributions to determine the mean heat flux and the mean normal contact pressure as functions of the separation between reference planes in the two surfaces. We find that the effective thermal conductance is an approximately linear function of nominal contact pressure, but it also increases with the square root of the sliding speed and decreases with the 3/4 power of the combined RMS roughness. The results can be used to define an effective thermal contact resistance and division of frictional heat in macroscale (e.g., finite element) models of engineering components, requiring as input only the measured roughness and material properties.

Appendices

Appendix 1

1.1 Effect of Relative Motion

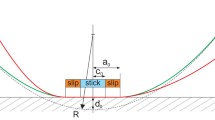
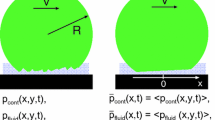
We consider the case where $C_2\gg C_1$, so that points on the surface of body 2 can be assumed to remain at temperature $T_2$ throughout the contact, and for simplicity we assume that $R_1=R_2=R$—i.e. the asperities on the two surfaces have the same summit radius $R$.

A representative point $(x,y)$ on the surface of body 1 will make contact as long as it remains within the appropriate contact circle in Fig. 2a—i.e. if $\xi ^2+\eta ^2\le a(t)^2$, where $\xi ,\eta$ and the time-varying contact radius $a(t)$ are defined in Eqs. (2, 7) respectively. Using these relations, the inequality can be written in terms of $x,y,t$ as

$$\begin{aligned} \left( x-\frac{Vt}{2}\right) ^2+\left( y-\frac{b}{2} \right) ^2\le \frac{Rd_0}{2}-\frac{V^2t^2}{8}, \end{aligned}$$

(47)

and hence

$$\begin{aligned} \frac{3\tau ^2}{2}-2X\tau +X^2+Y^2-\frac{1}{2}\le 0, \end{aligned}$$

(48)

where we define dimensionless time and coordinates through

$$\begin{aligned} X=\frac{x}{\sqrt{Rd_0}}; \quad Y=\frac{y}{\sqrt{Rd_0}}- \frac{b}{2\sqrt{Rd_0}}; \quad \tau =\frac{t}{t_0}= \frac{Vt}{2\sqrt{Rd_0}}. \end{aligned}$$

(49)

The times $\tau _1,\tau _2$ at which contact begins and ends at a given point $(X,Y)$ are defined by taking the equality in (48), giving

$$\begin{aligned} \tau _1,\tau _2=\frac{2}{3}\left( X\mp \sqrt{\frac{3}{4}- \frac{X^2}{2}-\frac{3Y^2}{2}}\right) . \end{aligned}$$

(50)

It follows that the period of contact at this point is

$$\begin{aligned} \Delta \tau =\tau _2-\tau _1 =\sqrt{\frac{4}{3}\left( 1-\frac{2X^2}{3}-2Y^2\right) }. \end{aligned}$$

(51)

Notice that by setting $\Delta \tau =0$, we define the envelope of the contact regions in Fig. 2a, which is

$$\begin{aligned} \frac{2x^2}{3}+2\left( y-\frac{b}{2}\right) ^2=Rd_0, \end{aligned}$$

(52)

using (49). Points outside this ellipse never experience contact. The total heat exchanged per unit area at $(X,Y)$ is given by Eq. (8) with $C_2\rightarrow \infty$ as

$$\begin{aligned} q=2C_1\theta \sqrt{\frac{\Delta t}{\pi }}=2C_1\theta (Rd_0)^{1/4}\sqrt{\frac{2\Delta \tau }{\pi V}} =\frac{4C_1\theta (Rd_0)^{1/4}}{3^{1/4}\sqrt{\pi V}}\left( 1-\frac{2X^2}{3}-2Y^2\right) ^{1/4} \end{aligned}$$

(53)

and hence the total heat exchange during the interaction is

$$\begin{aligned} Q_c=\int \int \limits _{\mathcal {A}}q(x,y)dxdy=Rd_0 \int \int \limits _{\mathcal {A}}q(X,Y)\text {d}X\text {d}Y, \end{aligned}$$

(54)

where the integration domain $\mathcal {A}$ comprises the ellipse of Eq. (52). We obtain

$$\begin{aligned} Q_c=\frac{8\root{4} \of {3}C_1\sqrt{\pi }\theta \left( d_0R \right) ^{5/4}}{5\sqrt{V}}=\frac{\root{4} \of {3}C_1\sqrt{2\pi } \theta \left( b_0^2-b^2\right) ^{5/4}}{5\sqrt{V}} , \end{aligned}$$

(55)

which exceeds Eq. (13) [with $R_1=R_2$] by a factor of $\root 4 \of {3}\approx 1.32$.

Appendix 2

1.1 Evaluation of Gaussian Integrals

Consider the integral

$$\begin{aligned} J(\gamma )=\frac{1}{2\pi \sigma _1\sigma _2}\int \limits _{-\infty }^\infty \int \limits _{h_0-h_2}^\infty \exp \left( -\frac{h_1^{2}}{2\sigma _1^{2}}-\frac{h_2^{2}}{2\sigma _2^{2}}\right) (h_1+h_2-h_0)^{\gamma }\text {d}h_1\text {d}h_2. \end{aligned}$$

We define dimensionless parameters

$$\begin{aligned} x_1=\frac{h_1}{\sigma _1\sqrt{2}}; \quad x_2=\frac{h_2}{\sigma _2\sqrt{2}} \end{aligned}$$

and then perform the linear transformation

$$\begin{aligned} \xi =\frac{x_1+\beta x_2}{\sqrt{1+\beta ^2}}; \quad \eta =\frac{\beta x_1-x_2}{\sqrt{1+\beta ^2}}\quad \text{ where }\quad \beta =\frac{\sigma _2}{\sigma _1}. \end{aligned}$$

This preserves the condition

$$\begin{aligned} \xi ^2+\eta ^2=x_1^2+x_2^2 \end{aligned}$$

so that the Jacobean of the transformation is unity. We also have

$$\begin{aligned} h_1+h_2-h_0=(\xi -\hat{h}_0)\sqrt{2(\sigma _1^2+\sigma _2^2)} \quad \text{ where }\quad \hat{h}_0=\frac{h_0}{\sqrt{2(\sigma _1^2+\sigma _2^2)}}, \end{aligned}$$

and the domain of integration in $J(\gamma )$ is $\xi >\hat{h}_0$, giving

$$\begin{aligned} J(\gamma )=\frac{[2(\sigma _1^2+\sigma _2^2)]^{\gamma /2}}{\pi } \int \limits _{\hat{h}_0}^\infty \int \limits _{-\infty }^\infty e^{-(\xi ^2+\eta ^2)}(\xi -\hat{h}_0)^{\gamma }\text {d}\eta \text {d}\xi . \end{aligned}$$

The integral with respect to $\eta$ evaluates to $\sqrt{\pi }$ so that finally we obtain

$$\begin{aligned} J(\gamma )=\frac{[2(\sigma _1^2+\sigma _2^2)]^{\gamma /2}}{\sqrt{\pi }} I(\hat{h}_0,\gamma ) \end{aligned}$$

(56)

where

$$\begin{aligned} I(\hat{h}_0,\gamma )=\int \limits _{\hat{h}_0}^\infty e^{-\xi ^2}(\xi -\hat{h}_0)^{\gamma }\text {d}\xi =\int \limits _0^\infty e^{-(y+\hat{h}_0)^2}y^{\gamma }\text {d}y, \end{aligned}$$

(57)

writing $y=\xi -\hat{h}_0$. The integral $I(\hat{h}_0,\gamma )$ can be evaluated in terms of special functions (for example using Mathematica or Maple) for integer and fractional values of $\gamma$.

1.2 Frictional Heating

Substituting $Q_f, \varPhi (b), \phi _1(h_1), \phi _2(h_2)$ from Eqs. (9, 22, 23) respectively into Eq. (24), we obtain

$$\begin{aligned} Q_f(S)=\frac{SN_1N_2\pi \mu E^{{*}}\sqrt{R_1R_2}}{2\sqrt{2}(R_1+R_2)^2}I_1, \end{aligned}$$

(58)

where

$$\begin{aligned} I_1=\frac{1}{2\pi \sigma _1\sigma _2}\int \limits _{-\infty }^\infty \int \limits _{h_0-h_2}^\infty \int \limits _0^{b_0} \exp \left( -\frac{h_1^{2}}{2 \sigma _1^{2}}-\frac{h_2^{2}}{2\sigma _2^{2}}\right) (b_0^2-b^2)^2\text {d}b\text {d}h_1\text {d}h_2 \end{aligned}$$

Evaluating the integral with respect to $b$ and substituting for $b_0$ from (5), we have

$$\begin{aligned} I_1=\frac{8[2(R_1+R_2)]^{5/2}}{15}\,J\left( \frac{5}{2}\right) . \end{aligned}$$

Substituting this result in (58) and using (56) we obtain

$$\begin{aligned} Q_f(S)=\frac{2^{21/4}N_1N_2 \sqrt{\pi }E^{{*}}\sqrt{R_1+R_2}\sqrt{R_1R_2}\mu S\left( \sigma _1^{2}+\sigma _2^{2} \right) ^{5/4}}{15} I\left( \hat{h}_0,\frac{5}{2}\right) . \end{aligned}$$

1.3 Heat Exchange Due to a Temperature Difference

Substituting $Q_c, \varPhi (b), \phi _1(h_1), \phi _2(h_2)$ from Eqs. (13, 22, 23) respectively into Eq. (27), we obtain

$$\begin{aligned} Q_c(S)=\frac{2^{7/2}\pi SN_1N_2C_1C_2\theta R^{{*}}}{5(C_1+C_2)(R_1+R_2)\sqrt{\pi V}}\,I_2, \end{aligned}$$

where

$$\begin{aligned} I_2&= \frac{1}{2\pi \sigma _1\sigma _2}\int \limits _{-\infty }^\infty \int \limits _{h_0-h_2}^\infty \int \limits _0^{b_0} \exp \left( -\frac{h_1^{2}}{2\sigma _1^{2}}- \frac{h_2^{2}}{2\sigma _2^{2}} \right) (b_0^2-b^2)^{5/4}\text {d}b\text {d}h_1\text {d}h_2 \\&= \frac{5\pi ^{3/2}[2(R_1+R_2)]^{7/4}}{21\sqrt{2}\Gamma (3/4)^2}J \left( \frac{7}{4}\right) \end{aligned}$$

after evaluating the integral with respect to $b$. We therefore have

$$\begin{aligned} Q_c(S)=\frac{2^{45/8}\pi ^{3/2}SN_1N_2C_1C_2\theta R_1R_2(\sigma _1^2+\sigma _2^2)^{7/8}}{21 \Gamma (3/4)^2(C_1+C_2)(R_1+R_2)^{1/4}\sqrt{V}}I \left( \hat{h}_0,\frac{7}{4}\right) . \end{aligned}$$