Abstract
The paper asks whether diagrams in mathematics are particularly fruitful compared to other types of representations. In order to respond to this question a number of examples of propositions and their proofs are considered. In addition I use part of Peirce’s semiotics to characterise different types of signs used in mathematical reasoning, distinguishing between symbolic expressions and 2-dimensional diagrams. As a starting point I examine a proposal by Macbeth (Realising reason. A narrative of truth & knowing, Oxford University Press, Oxford, 2014). Macbeth explains how it can be that objects “pop up”, e.g., as a consequence of the constructions made in the diagrams of Euclid, that is, why they are fruitful. It turns out, however, that diagrams are not exclusively fruitful in this sense. By analysing the proofs given in the paper I introduce the notion of a ‘faithful representation’. A faithful representation represents as either an image (resembling what it stands for) or as a metaphor (sharing some underlying structure). Secondly it represents certain relevant relations (that is, as an iconic diagram in Peirce’s terminology). Thirdly manipulations on the representations respect manipulations on the objects they represent, so that new relations may be found. The examples given in the paper illustrate how such representations can be fruitful. These examples include proofs based on both symbolic expressions as well as diagrams and so it seems diagrams are not special when it comes to fruitfulness. Having said this, I do present two features of diagrams that seem to be unique. One consists of the possibility of exhibiting the type of relation in a diagram—or simply showing that a relation exists—as a contrast to stating in words that it exists. The second is the spatial configurations possible when using diagrams, e.g., allowing to show multiple relations in a single diagram.







Similar content being viewed by others
Notes
Conversely icons, indices and symbols can be taken as the different possibilities of an object to act on a sign so that the sign may be taken to represent it.
(CP 2.282) refers to paragraph 282 in the second volume of Peirce’s Collected Papers edited by Hartshorne and Weiss listed as (Peirce 1965–1967) in the bibliography.
Carter (2012a, forthcoming) give further examples of how metaphors are used in mathematics.
In a paper published in 1885 Peirce characterises an index as follows: “the sign [index] signifies its object solely by virtue of being really connected with it. Of this nature are all natural signs and physical symptoms. I call such a sign an index ...The index asserts nothing; it only says ‘There!” It takes hold of our eyes, as it were, and forcibly directs them to a particular object, and there it stops. Demonstrative and relative pronouns are nearly pure indices, because they denote things without describing them; so are the letters on a geometric diagram, and the subscript numbers which in algebra distinguish one value from another without saying what those values are”(CP 3.361).
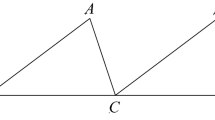
In order to explain the various meanings of a diagram as a noun I give a couple of examples from Euclid’s Elements. If the purpose of the diagram was to illustrate the statement of the proposition of, e.g., proposition I.1 (see Fig. 5), a drawing of an equilateral triangle would suffice. Note also that the shown diagram most often do not show how the marked points would actually be constructed. In order to, for example, divide a line segment in two one needs to draw both circles shown in Fig. 5 and a line joining their intersection points. In Euclid proposition II.11 (Fig. 1) the line segment AC is divided in two in the point named E, but the diagram does not show how to construct it. Instead the diagram mainly shows the geometric figures and points necessary to follow the demonstration.
Following Euclidean tradition the diagram is lettered following the alphabet, indicating that the “given” is the line AB.
One is supposed to note that ABCD is a square, so that \(AB=BD\).
Euclid II.6 states that: If a straight line be bisected and a straight line be added to it in a straight line, the rectangle contained by the whole with the added straight line and the added straight line together with the square on the half is equal to the square on the straight line made up on the half and the added straight line. Given such long statements without using any letters as cognitive fix-points also points to a role that the geometric figures must play. The parts of the figure, that is, the line segments and the various mentioned figures (squares or rectangles), may serve as the units that the statement is about.
A permutation \(\pi =(12)(36)(45)\) means that the element 1 is mapped to 2, 2 is mapped to 1, 3 is mapped to 6 and so on. See also Fig. 2.
This theorem corresponds to lemma 1.17 in Haagerup and Thorbjørnsen (1999). The lemma states that a non-crossing permutation has a pair of neighbours. The proof is by contradiction, so one assumes the permutation has no neighbours and proves a crossing must occur.
This feature of proofs is also described by Macbeth (2014, pp. 60–68) who characterises the language used in such proofs as giving instructions on how to reason in contrast to languages displaying the reasoning. Macbeth claims Euclidean diagrams are tools used to display reasoning.
Similarly Hilbert showed in his various versions of the Foundations of Geometry (building on Pasch’s earlier work) that it was possible to reason in geometry without referring to figures, that is, basing inferences on axioms. This does not mean, however, that diagrams are excluded from these books.
Note that it is possible to find examples of proofs in mathematics where a particular diagram can be said to individuate a proposition. One such example is the diagram accompanying the Snake lemma. There are also examples of results in contemporary mathematics that depend on diagrams as shown in, for example De Toffoli and Giardino (2015).
Macbeth contrasts diagrammatic reasoning with ‘picture proofs’ that depend on multiple readings but are not fruitful in the same sense as the use of diagrams in Euclid’s Elements. As an example of picture proofs she mentions Venn diagrams.
Macbeth refers to Ken Manders who has introduced this notion, see e.g., his (2008).
In Carter (2012a) a different type of multiple reading of signs is described. It is noted that mathematics employs ‘compound definitions’ that is definitions of concepts may contain several components. A simple example is the definition of a prime number which both fulfils the definition of a prime and is a natural number.
This proof is a modification of the proof given in algebra text book by Hungerford (1997, pp. 194–195).
A group \((G, \cdot )\) is a set, G, together with an operation \(\cdot : G\times G \rightarrow G\) fulfilling the following axioms. Associativity for all \(a, b, c\in G\), \(a\cdot (b\cdot c)= (a\cdot b)\cdot c\), neutral element there exists an element \(e\in G\) such that for all \(a\in G\)\(a\cdot e =e\cdot a =a\) and inverse element for all \(a\in G\) there exists \(a^{-1}\in G\) such that \(a\cdot a^{-1}=a^{-1}\cdot a=e\). Note that I have chosen to write the operation multiplicatively.
As an example of a practice that for some purposes turned out to be advantageous, one could mention Descartes’ introduction of analytic geometry. This practice has advantages over the previous geometric practice. One could mention the fact that when performing geometric proofs one has sometimes to make case distinctions, taking into account, e.g., whether an angle is right, obtuse or acute. That is, one may have to produce three proofs whereas the algebraic proof takes care of all cases at once. One could also state that the modern calculus is an immense improvement (that is, cognitive advantage) compared to the various methods used before Newton and Leibniz. In calculus one has methods (e.g., computing an integral) that applies to any given (reasonable) function.
When referring to attention shifts and category specification I am freely using Giaquinto’s (2007) account of a theory on visual imagery formulated by Stephen Kosslyn. ‘Category specifications’ is defined as a “set of feature descriptions stored more or less permanently”(p. 108). A set of specifications for a triangle would contain that it is a plane surface region and that is composed of three straight lines.
The calculations done in order to determine a could be as follows. First b is isolated in the second identity giving \(b=ax\). This is inserted in the first giving \(a^2+(ax)^2=1\). Isolating \(a^2\) one obtains \(a^2(1+x^2)=1\), dividing by \((1+x^2)\) on both sides and finally taking the square-root gives \(a=\pm \frac{ 1}{\sqrt{1+x^2}}\).
Macbeth argues that the two functions \(\cos (x)\) and \(\sin (x)\)pop up as a result of the algebraic manipulations made on the terms in the power series expansion of \(e^x\).
Macbeth introduces a similar distinction. She distinguishes between languages where one reasons ‘on the signs’ and in the signs. One reasons on the signs when the signs can be taken to correspond to the objects one reasons about. This is what is observed in the case of Euler’s formula. In contrast she argues one reasons in the diagrams of Euclid.
References
Carter, J. (2010). Diagrams and proofs in analysis. International Studies in the Philosophy of Science, 24, 1–14.
Carter, J. (2012a). The role of representations in mathematical reasoning. Philosophia Scientiae, 16(1), 55–70.
Carter, J. (2012b). The role of representations for understanding. Notae Philosophicae Scientiae Formalis, 1(2), 135–147.
Carter, J. (forthcoming). Graph-algebras—Faithful representations and mediating objects in mathematics. To appear in the special issue ‘Tools of reason: The practice of scientific diagramming from antiquity to the present’ in the journal Endeavour.
Catton, P., & Montelle, C. (2012). To diagram, to demonstrate: To do, to see, and to judge in Greek geometry. Philosophia Mathematica, 20, 25–57.
De Toffoli, S., & Giardino, V. (2015). An Inquiry into the practice of proving in low-dimensional topology. In G. Lolli, et al. (Eds.), From logic to practice. Italian studies in the philosophy of mathematics. Boston studies in the philosophy and history of science (Vol. 308, pp. 315–336). Basel: Springer.
Euclid (1956). The thirteen books of Euclid’s Elements. Translated with introduction and commentary by Sir Thomas L. Heath. 2nd edition unabridged. New York: Dover Publications, Inc.
Giaquinto, M. (2007). Visual thinking in mathematics. Oxford: Oxford University Press.
Grosholz, E. (2007). Representation and productive ambiguity in mathematics and the sciences. New York: Oxford University Press.
Haagerup, U., & Thorbjørnsen, S. (1999). Random matrices and K-theory for exact \(C^*-\)algebras. Documenta Mathematica, 4, 341–450.
Hungerford, T. W. (1997). Abstract algebra: An introduction (2nd ed.). Orlando, FL: Saunders College Publishing.
Macbeth, D. (2010). Diagrammatic reasoning in Euclid’s Elements. In B. Van Kerkhove, J. De Vuyst, & J. P. Van Bendegem (Eds.), Philosophical perspecives on mathematical practice (pp. 235–267). Milton Keynes: College Publications.
Macbeth, D. (2014). Realising reason. A narrative of truth & knowing. Oxford: Oxford University Press.
Mancosu, P. (2005). Visualisation in logic and in mathematics. In P. Mancosu, K. F. Jørgensen, & S. A. Pedersen (Eds.), Visualization, explanation and reasoning styles in mathematics (pp. 13–30). Dordrecht: Springer.
Manders, K. (1999). Euclid or Descartes? Representation and responsiveness. Unpublished draft.
Manders, K. (2008). The Euclidean diagram. In P. Mancosu (Ed.), The philosophy of mathematical practice (pp. 80–133). New York: Oxford University Press.
Netz, R. (1999). Shaping of deduction in Greek mathematics. West Nyack, NY: Cambrigde University Press.
Peirce, C. S. (1965–1967). Collected papers of Charles Sanders Peirce. Edited by Charles Hartshorne and Paul Weiss. Volumes I–IV third printing. Cambridge, Massachusetts: The Belknap Press of Harvard University Press.
Tappenden, J. (2005). Proof style and understanding in mathematics I: Visualization, unification and axiom of choice. In P. Mancosu, K. F. Jørgensen, & S. A. Pedersen (Eds.), Visualization, explanation and reasoning styles in mathematics (pp. 147–214). Dordrecht: Springer.
Author information
Authors and Affiliations
Corresponding author
Additional information
I especially thank Danielle Macbeth for comments on earlier versions of this paper. Furthermore I wish to thank the anonymous referees provided by Synthese for their helpful comments.
Rights and permissions
About this article
Cite this article
Carter, J. Exploring the fruitfulness of diagrams in mathematics. Synthese 196, 4011–4032 (2019). https://doi.org/10.1007/s11229-017-1635-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1635-1