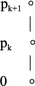Abstract
I present a new approach to the logic and semantics of vagueness.
Similar content being viewed by others
Notes
The one exception appears to be Zardini (2014), although his view appears to be very different from mine in a number of fundamental respects.
The ideas behind my approach were first presented in a seminar on vagueness that I gave at NYU in the Fall of 2008. I should like to thank the participants—including Hartry Field, Stephen Schiffer and Crispin Wright—for many helpful comments. I should also like to thank two referees for the journal and the audiences at talks I gave at Austin Texas, Texas A&M and MIT; and I am, in addition, indebted to Robbie Williams and John Hawthorne for some stimulating conversations. The paper provides only a very brief exposition of the basic ideas; and I hope to give a much fuller exposition of both the philosophical and logical aspects of the theory elsewhere.
I should make clear that I am only interested in the extensional notion of indeterminacy, indeterminacy in so far as it relates to the actual rather than the possible application of the predicate; and, for simplicity, I have focused on the vagueness of predicates, although the discussion is readily extended to other forms of expression.
I am here presupposing a context in which each proposition \(\hbox {p}_ \mathrm{k}\) is equivalent to its double negation \(\lnot \lnot \hbox {p}_ \mathrm{k}\). In the absence of this assumption, the state-descriptions should be formed, not from \(\hbox {p}_\mathrm{1},\, \hbox {p}_\mathrm{2}, \ldots , \hbox {p}_\mathrm{n}\), but from their negations \(\lnot \hbox {p}_\mathrm{1},\, \lnot \hbox {p}_\mathrm{2}, \ldots , \lnot \hbox {p}_\mathrm{n}\).
Principally, the equivalence of \(\lnot (\hbox {p} \vee \hbox {q})\) to \(\lnot \hbox {p}\wedge \lnot \hbox {q}\) and the equivalence of \((\hbox {p}\vee \hbox {q})\wedge \hbox {r to }(\hbox {p}\wedge \hbox {r})\vee (\hbox {q}\vee \hbox {r}).\) I should note that the proof of equivalence will go through within the logic of vagueness given below.
It is perhaps partly for this reason - a failure of logical nerve, so to speak - that the present approach to vagueness has not previously been pursued. The closest semantical framework in the literature of which I am aware is the relational semantics for quantum logic found in Goldblatt (1974), but the motivation and background to the two approaches has been so very different that they have not been connected. There is also a resemblance in motivation between my Compatibility Semantics and Brandom’s Incompatibility Semantics from the fifth of his John Locke Lectures, but the similarity ends there and the development of the same general idea is very different.
For simplicity, I do not consider the semantical treatment of the quantifiers.
The same model can be used to establish the satisfiability of \(\lnot [(\lnot \hbox {p}\vee \lnot \lnot \hbox {p}) \wedge (\lnot \hbox {q}\vee \lnot \lnot \hbox {q})]\).
If we do not assume the equivalence of p and \(\lnot \lnot \hbox {p}\) then, strictly speaking, indeterminacy should be taken to be the denial of a conjunction of instances of the form \(\lnot \hbox {p}_ \mathrm{k} \vee \lnot \lnot \hbox {p}_ \mathrm{k}\).
This kind of move is familiar from the literature. For Putnam (1983) observed that the reasoning above requires the use of Double Negation Elimination and so would not go through in intuitionistic logic; and Read and Wright (1985) then pointed out that the use of Double Negation Elimination might be avoided by running the argument backwards. But, of course, we can see in principle that the adoption of intuitionistic logic is of no help in resisting the derivation of a contradiction, at least when the argument is stated in sentential form. For it is a general result that any contradiction that can be derived classically can also be derived intuitionistically (though not necessarily by the same route). Thus the reverse derivation above just shows how, in this particular case, the alternative derivation might proceed.
Suppose that A and \(\hbox {A }\supset \hbox { B}\) are true under a given use. Then B must also be true under that use by the clause for \(\supset \), thereby establishing the validity of modus ponens. Now suppose that \(\lnot \hbox {A}\) and \(\hbox {A }\vee \hbox { B}\) are true under a given use. Then either A is true under that use or B is by the clause for \(\vee \). But A is not true under the use by the clause for \(\lnot \); and so B must be true under the use, thereby establishing the validity of disjunctive syllogism. Finally, the inference from A and \(\lnot (\hbox {A }\wedge \hbox { B})\) to \(\lnot \hbox {B}\) will be valid under the assumption of \(\hbox {B }\vee \lnot \hbox {B}\). For either B or \(\lnot \hbox {B}\) will be true under the given use; and the former will be impossible given that A and \(\lnot (\hbox {A }\wedge \hbox { B})\) are true under the given use.
More formally, consider the model depicted below:
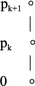
with \(\hbox {p}_ \mathrm{k+1}\)—for \(b_\mathrm{k+1}\) is bald—true at point \(\hbox {p}_ \mathrm{k+1}\hbox { and }\hbox {p}_ \mathrm{k}\)—for \(b_{\mathrm{k}}\) is bald—true at point \(\hbox {p}_ \mathrm{k}\) (and that is all). Then we readily verify that: \(\lnot \hbox {p}_ \mathrm{k+1}\) is true at the base point 0; that \(\hbox {p}_ \mathrm{k}\) is not true at 0 and \(\lnot \hbox {p}_ \mathrm{k+1}\) is not true at \(\hbox {p}_ \mathrm{k}\) and hence that \(\lnot (\hbox {p}_\mathrm{k} \wedge \lnot \hbox {p}_{\hbox {k}+\hbox {1}} )\) is true at the base point; and that \(\hbox {p}_ \mathrm{k}\) is true at \(\hbox {p}_ \mathrm{k}\) and hence that \(\lnot \hbox {p}_ \mathrm{k}\) is not true at 0. This establishes the failure of the relevant instance of Conjunctive Syllogism at 0, with \(\lnot \hbox {p}_ \mathrm{k+1}\) and \(\lnot (\hbox {p}_\mathrm{k} \wedge \lnot \hbox {p}_{\hbox {k}+\hbox {1}} )\) true at 0 but \(\lnot \hbox {p}_ \mathrm{k}\) not true at 0. We also readily verify that: \(\hbox {p}_ \mathrm{k+1}\) is not true at 0 and hence, given that \(\lnot \hbox {p}_ \mathrm{k}\) is not true at 0, that \(\lnot \hbox {p}_\mathrm{k} \vee \hbox {p}_{\hbox {k}+\hbox {1}} \) is not true at 0; and that \(\hbox {p}_ \mathrm{k}\) is true at \(\hbox {p}_ \mathrm{k}\) while \(\hbox {p}_ \mathrm{k+1}\) is not true at \(\hbox {p}_ \mathrm{k}\) and hence, given that \(\hbox {p}_ \mathrm{k}\) is not true at 0, that \(\hbox {p}_\mathrm{k} \supset \hbox {p}_{\hbox {k}+\hbox {1}} \) is not true at 0. This establishes that the disjunctive version \(\lnot \hbox {p}_\mathrm{k} \vee \hbox {p}_{\hbox {k}+\hbox {1}} \) and the conditional version \(\hbox {p}_\mathrm{k} \supset \hbox {p}_{\hbox {k}+\hbox {1}} \) of the major premiss are not true at 0.
I am not so rash as to make any claims about how my conception of a transcendental illusion relates to Kant’s.
I use the phrase ‘not-true’ rather than ‘not true’, since I do not wish to prejudge the question of whether ‘not-true’ is the negation of ‘true’. In fact, the relevant sense of not-true is provably undefinable within our system.
Use \({\bar{\hbox {T}}}\hbox {A}\) for it is not-true that A. We might then justify the inference from \(\lnot \left( \hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B} \right) \) to \(\hbox {A} \supset \hbox {B}\) in terms of the compatibilist semantics. For take \({\bar{\hbox {T}}}\hbox {(A)}\) to be true at a use \(u\) iff A is not true at \(u\). Suppose now that \(\lnot \left( {\hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B}} \right) \) is true at the use \(u\). Take any \(v\) compatible with \(u\) at which A is true. Then B is true at \(v\) since otherwise \({\bar{\hbox {T}}}\hbox {B}\) would be true at \(v\) and, consequently, \(\left( \hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B} \right) \) would be true at v and so \(\lnot \left( {\hbox {A} \wedge {\bar{\hbox {T}}}\hbox {B}} \right) \) would not be true at \(u\) after all.
The response A will also be in competition with \({\bar{\hbox {T}}}\hbox {A}\) in the sense that there is no use of any model in which both are true.
Discussed, for example, in Graff (2001).
Williamson (1994, 1999) and Gaifman (2010) impose reflexivity and symmetry on the accessibility relation in giving a semantics for the definitely operator; and Goldblatt (1974) imposes reflexivity and symmetry on a corresponding compatibility relation in giving a semantics for negation. But we do not use the compatibility relation to provide a semantics for the definitely operator (which we regard as illegitimate); we do not insist upon a double negation interpretation of propositions, as in Goldblatt (1974), and therefore allow ourselves to introduce a choice form of disjunction; and we adopt a novel account of the conditional. Most significantly of all, our semantics is motivated by the desire to avoid the impossibility theorem, which is not something that is aimed for under these alternative approaches.
References
Black, M. (1937). Vagueness: an exercise in logical analysis. Philosophy of Science, 4(4), 427–455.
Evans, G. (1978). Can there be vague objects. Analysis, 38, 208.
Field, H. (1994). Disquotational truth and factually defective discourse. Philosophical Review, 103, 405–452.
Fine, K. (1975). Vagueness, truth and logic. Synthese 30, 265–300. Reprinted in Keefe & Smith (eds.). (1996). Vagueness: A reader. Boston: MIT University Press.
Fine, K. (2008). The impossibility of vagueness. Philosophical Perspectives, 22(1), 111–116.
Gaifman, H. (2010). Vagueness, tolerance and contextual logic. Synthese, 174, 5–46.
Goldblatt, R. (1974). Semantic analysis of orthologic. Journal of Philosophical Logic, 3, 19–35.
Graff, D. (2001). Phenomenal continua and the sorites. Mind, 110(440), 905–935.
Greenough, P. (2003). Vagueness: A minimal theory. Mind, 112(446), 235–281.
McGee, V. (1985). A counter-example to Modus Ponens. Journal of Philosophy, 82(9), 462–471.
Peirce, C. S. (1902). The collected papers. Harvard: Harvard University Press.
Putnam, H. (1983). Vagueness and alternative logic, Erkenntis 19, 297–314. Reprinted in his Realism and reason (pp. 271–86). Cambridge: Cambridge University Press.
Read, S., & Wright, C. (1985). Hairier than Putnam thought. Analysis, 45, 56–58.
Southern Journal of Philosophy, (1998). Distinctions without a difference. 33(Supplement 1995), 203–251.
Williamson, T. (1994). Vagueness. London: Routledge.
Williamson, T. (1999). On the structure of higher order vagueness. Mind, 103, 127–143.
Wright, C. (2003). Vagueness: A fifth column approach. In J. C. Beall & M. Glanzburg (Eds.), Liars and heaps: New essays on paradox (pp. 84–105). Oxford: Oxford University Press.
Zardini E. (2014). First-order tolerant logics. Review of Symbolic Logic (forthcoming).
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
We deal with a propositional language in which formulas are formed from an infinite set SL of sentence letters \(\hbox {p}_\mathrm{1}\), \(\hbox {p}_\mathrm{2}\), ...by means of the connectives \(\vee \), \(\wedge , \lnot ,\) and \(\supset \) We shall also find it convenient to use the falsum constant \(\bot \) in place of \(\lnot \), defining \(\lnot \)A as A \(\supset \bot \).
1.1 Intuitionistic Semantics
We begin by reminding the reader of the Kripke semantics for intuitionistic logic. This will then serve as a foil for our own compatibilist-style semantics.
Under the Kripke semantics, a model M is a triple (\(U\), \(\le \), \(\upvarphi )\), where:
- I(i):
-
\(U\) (‘points’ or ‘uses’) is a non-empty set;
- I(ii):
-
\(\le \) (extension) is a reflexive and transitive relation on U;
- I(iii):
-
\(\upvarphi \) (valuation) is a function from SL into
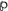
(U) subject to the Hereditary Condition:
$$\begin{aligned} u\in \upvarphi \left( \hbox {p} \right) \; \mathrm{{and}} \; u \le { {v}} \hbox { implies } { {v}}\in \upvarphi \left( \hbox {p} \right) \hbox { for } \hbox { all } u,{ {v}}\in U \hbox { and } \hbox { p} \in \hbox { SL}. \end{aligned}$$
Intuitively, we may think of \(U\) as consisting of hypothetical uses of the predicates of the language; \(\le \) is the extension relation, where one use extends another when anything taken to be true under the second use is taken to be true under the first; and \(\upvarphi \) tells us which sentence letters are true under any given use.
Relative to a model M, truth of a formula A under the use \(u\) (\(u~{\vert }\!= \hbox {A}\)) is defined by the following clauses:
- T(i):
-
\(u\,|{=\hbox { p iff }} u \in \upvarphi \left( \hbox {p} \right) \)
- T(ii):
-
\(u\,|{=\hbox { B}}\wedge \hbox {C} \hbox { iff }\, u\,\left| \!\,{=\hbox { B} \hbox { and}}\, u\, \right| \!\,{=\,\hbox { C}}\)
- T(iii):
-
\(u\,|{=\hbox { B}}\vee \hbox {C iff }\, u\,\left| \!\,{=\hbox { B or}\, u}\, \right| \!\,{=\hbox { C}}\)
- T(iv):
-
\(u\,|{=\lnot \hbox {B iff not }} { {v}}\,|{=\hbox { B for any }} v \hbox { for which}\, u\le { {v}}\)
- T(v):
-
\(u\,|{=\hbox { B}}\supset \hbox {C iff } { {v}}\,\left| {={\hbox { C whenever}}\, { {v}}} \,\right| {=\hbox { B} \hbox { and}}\, u\,\le { {v}}.\)
We may also employ the following clause for \(\bot \) in place of the clause for \(\lnot \):
- T(vi):
-
\(\hbox {never}\, u\,|\!=\bot .\)
We adopt some standard logical terminology. A is said to be a consequence of \(\Delta \)—in symbols, \(\Delta {\vert }\!=\hbox { A}\)—if, for any model M and point \(u\) of M, A is true at \(u\) in M whenever \(\Delta \) (i.e. each formula of \(\Delta )\) is true at \(u\) in M. We say that A is valid—in symbols, \({\vert }\!= \hbox {A}\)—if A is a consequence of the empty set of formulas \(\oslash \), i.e. if A is true at any point in any model; and we say that A is equivalent to B—in symbols,\(\hbox { A}=\!{\vert }{\vert }\!=\hbox { B}\)—if \(\hbox {A}{\vert }\!=\hbox { B}\) and \(\hbox {B }{\vert }\!=\hbox { A}\). The formulas of \(\Delta \) are said to satisfiable if for some model M and point \(u\) of M, \(\Delta \) is true at \(u\) in M; and the formulas of \(\Delta \) are said to be compatible with the formula A (or with the set of formulas \(\Gamma )\) if \(\Delta \quad \cup \) {A} (or \(\Delta \quad \cup \quad \Gamma )\) is satisfiable (and similarly for unsatisfiability). Clearly, the formulas \(\Delta \) are satisfiable iff not \(\Delta {\vert }\!= \bot \).
1.2 The Compatibilist Semantics
Under the compatibilist semantics, we take a model M to be a triple (\(U\), \(\circ \), \(\upvarphi )\), where:
- C(i):
-
\(U\) (‘points’ or ‘uses’) is a non-empty set;
- C(ii):
-
\(\circ \) (compatibility) is a reflexive and symmetric relation on \(U\);
- C(iii):
-
\(\upvarphi \) (valuation) is a function from SL into
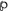
(U).
Our intuitive understanding of \(U\) and of \(\upvarphi \) is as before.
Relative to a model M, truth of a formula A under a use \(u\, (u\, {\vert }=\hbox { A}\)) is defined by the following clauses:
- T(i):
-
\(u\,|{=\hbox { p iff }} u\in \upvarphi \left( \hbox { p} \right) \)
- T(ii):
-
\(u\,|{=\hbox { B}}\wedge \hbox {C iff }\, u\,\left| {=\hbox { B and}\, u} \,\right| {=\hbox { C}}\)
- T(iii):
-
\(u\,|{=\hbox { B}}\vee \hbox {C iff } u\,\left| {=\hbox { B or}\, u}\, \right| {=\hbox { C}}\)
- T(iv):
-
\(u\,\left| {=\lnot \hbox {B iff not}\, { {v}}}\, \right| {=\hbox { B for any}}\, { {v}}\, \hbox {for which }\, u\circ { {v}}\)
- T*(v):
-
\(u\,|{=\hbox { B}}\supset \hbox {C iff either }\left( \hbox {a} \right) \,u\,\left| {=\hbox { B and}\, u} \,\right| {=\hbox { C or }}\left( \hbox {b} \right) { {v}}\left| {=\hbox { C whenever }} { {v}}\, \right| {=\hbox { B and }} u\circ { {v}}\)
- T(vi):
-
\(\hbox {never}\, u\,|{=\bot } .\)
There are two main changes from the semantics for intuitionist logic. The first is in the substitution of the reflexive and symmetric relation \(\circ \) for the reflexive and transitive relation \(\le \) (along with the elimination of the hereditary condition); and the second is in the modification of the clause for the conditional (T*(v) in place of T(v)). The new clause might be regarded as a form of the ‘closest world’ semantics; for either the closest B-world is the actual world \(u\), in which case C must also be true in \(u\), or else the closest B-worlds are the worlds compatible with the actual world, in which case C must also be true in those worlds. Thus there are two ways in which the conditional B \(\supset \) C can be true at a point—either ‘truth-functionally’ with both B and C true or ‘strictly’ with C true whenever B is true.Footnote 17
Logical notions such as validity and consequence transfer in the obvious way to the present semantics. When there is a need to distinguish the semantics in question, we shall talk of compatibilitist or C-validity versus intuitionistic or I-validity; and similarly when other semantical frameworks are in question. We may also define a natural notion of disagreement, where two sets of formulas \(\Delta \) and \(\Gamma \) are said to be in disagreement—\(\Delta \bullet \Gamma \)—if in any model, never \(u\, {\vert }\!= \Delta \), \({ {v}}\ {\vert }\!= \Gamma \) and \(u \circ { {v}}\).
We present three central results—Completeness, Inclusion and Possibility—which we state without proof (further details will be provided elsewhere). Let CL (compatibilist logic) be the system defined by the following axioms and rules of inference (with \(\bot \) as primitive):
1.3 Axioms
-
A1.
\(\hbox {A}\wedge (\hbox {A}\supset \hbox {B})\supset \hbox {B}\)
-
A2.
\(\hbox {A}\supset ((\hbox {A}\supset \hbox {B})\supset \hbox {B})\)
-
A3.
\(\hbox {A}\supset (\hbox {B}\supset \hbox {B})\)
-
A4.
\(\hbox {A}\wedge \hbox {B}\supset (\hbox {A}\supset \hbox {B})\)
-
A5.
\((\hbox {A}\supset \hbox {B}\wedge \hbox {B}\supset \hbox {C})\supset \hbox {B}\vee (\hbox {A}\supset \hbox {C})\)
-
A6.
\(\hbox {A}\wedge \hbox {B}\supset \hbox {A}\)
-
A7.
\(\hbox {A}\wedge \hbox {B}\supset \hbox {B}\)
-
A8.
\((\hbox {A}\supset \hbox {B}\wedge \hbox {A}\supset \hbox {C})\supset (\hbox {A}\supset \hbox {B}\wedge \hbox {C})\)
-
A9.
\(\hbox {A}\supset \hbox {A}\vee \hbox {B}\)
-
A10.
\(\hbox {B}\supset \hbox {A}\vee \hbox {B}\)
-
A11.
\(((\hbox {A}\supset \hbox {C})\wedge (\hbox {B}\supset \hbox {C}))\supset ((\hbox {A}\vee \hbox {B})\supset \hbox {C})\)
-
A12.
\(\hbox {A}\wedge (\hbox {B}\vee \hbox {C})\supset (\hbox {A}\wedge \hbox {B})\vee (\hbox {A}\wedge \hbox {C}).\)
-
A13.
\(\bot \supset \hbox {A}.\)
1.4 Rules of inference
-
R1.
\(\hbox {A},\hbox { A}\supset \hbox {B}/\hbox { B}\)
-
R2.
\(\hbox {A},\hbox { B }/\hbox { A}\wedge \hbox {B}\)
-
R3.
\(\hbox {A}\supset \hbox {B},\hbox { B}\supset \hbox {C }/\hbox { A}\supset \hbox {C}\)
Theorem 1
(Completeness) A formula A is a theorem of the system CL iff it is valid under the compatiblist semantics.
The above axiom system is perhaps a little unnatural, but I believe a much more natural system can be obtained using disagreement—\(\Delta \, {\bullet } \,\Gamma \)—as the basic meta-logical primitive in place of theoremhood; and, indeed, the resulting system may well be regarded as a basic way to formalize the logic of disagreement.
We also have:
Theorem 2
(Inclusion) Any theorem of compatibilist logic is a theorem of intuitionistic logic.
This inclusion is proper, since \(\hbox {p}\wedge \lnot (\hbox {p}\wedge \hbox {q})\supset \lnot \hbox {q}\) is a theorem of intuitionistic logic but not of compatibility logic.
To state the third result, we need some terminology from Fine (2008). A (collective) response is a sequence A(p), A(p),..., A(p) of formulas constructed from the sentence letter p; and \(\hbox {A}_{1}, \hbox {A}_{2}, \ldots , \hbox {A}_\mathrm{n}\) is said to be a (collective)response to \(\hbox {B}_{1}, \hbox {B}_{2}, \ldots , \hbox {B}_\mathrm{n}\) if \(\hbox {A}_{1}, \hbox {A}_{2}, \ldots , \hbox {A}_\mathrm{n}\) are respectively of the form \(\hbox {A}_{1}(\hbox {B}_{1}),\hbox { A}_{2}(\hbox {B}_{2}), \ldots ,\hbox { A}_\mathrm{n}(\hbox {B}_\mathrm{n})\), where \(\hbox {A}_{1}\hbox {(p)},\hbox { A}_{2}\hbox {(p)}, \ldots ,\hbox { A}_\mathrm{n}\hbox {(p)}\) is a collective response. We say that the collective response \(\hbox {A}_{1}, \hbox {A}_{2}, \ldots ,\hbox { A}_\mathrm{n}\) is sharp if:
-
(i)
\(\hbox {A}_\mathrm{i} \ne \hbox {A}_\mathrm{j}\ \hbox {for some i},\hbox { j}\le \hbox {n};\)
-
(ii)
\(\hbox {A}_\mathrm{i}\ \hbox {is incompatible with A}_\mathrm{j}\ \hbox {or A}_\mathrm{i} =\hbox { A}_\mathrm{j}\ \hbox {whenever 1}\le \hbox {i }<\hbox { j}\le \hbox {n}.\)
We may similarly talk of a sharp response to \(\hbox {B}_\mathrm{1}\), \(\hbox {B}_\mathrm{2}\), ..., \(\hbox {B}_\mathrm{n}\). We use:
The indeterminacy operator I* can then be employed to evade the impossibility result of Fine (2008).
Theorem 3
(Possibility) For n \(\ge \) 2, I*(p\(_{1}\), p\(_{2}\), ..., p\(_{\mathrm{{n}}+1}\)) is compatible with \(\{ \mathrm{{p}}_1, \lnot \mathrm {p}_{\mathrm{{n}}+1}\}\) and incompatible with any sharp response to p\(_{1}\), p\(_{2}\), ..., p\(_{\mathrm{{n}}+1}\).
This is a fundamental result and shows how vagueness, as we naturally conceive it, is indeed possible.
Rights and permissions
About this article
Cite this article
Fine, K. The possibility of vagueness. Synthese 194, 3699–3725 (2017). https://doi.org/10.1007/s11229-014-0625-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-014-0625-9