Quantum correlations responsible for remote state creation: strong and weak control parameters

Abstract

We study the quantum correlations between the two remote qubits (sender and receiver) connected by the transmission line (homogeneous spin-1/2 chain) depending on the parameters of the sender’s and receiver’s initial states (control parameters). We consider two different measures of quantum correlations: the entanglement (a traditional measure) and the informational correlation (based on the parameter exchange between the sender and receiver). We find the domain in the control parameter space yielding (i) zero entanglement between the sender and receiver during the whole evolution period and (ii) non-vanishing informational correlation between the sender and receiver, thus showing that the informational correlation is responsible for the remote state creation. Among the control parameters, there are the strong parameters (which strongly effect the values of studied measures) and the weak ones (whose effect is negligible), therewith the eigenvalues of the initial state are given a privileged role. We also show that the problem of small entanglement (concurrence) in quantum information processing is similar (in certain sense) to the problem of small determinants in linear algebra. A particular model of 40-node spin-1/2 communication line is presented.

Appendix

1.1 Permanent characteristics of communication line

Writing $\rho ^{SR}$ (8) in components, we have

$$\begin{aligned} \rho ^{SR}_{i_1 i_N; j_1 j_N} = T_{i_1 i_N l_1 l_N;j_1 j_N k_1k_N}(\rho ^S_0)_{l_1; k_1}(\rho ^R_0)_{l_N; k_N}. \end{aligned}$$

(34)

Here all the indexes take two values 0 and 1, the parameters $T_{i_1 i_N l_1 l_N;j_1 j_N k_1k_N}$ in this formula depend on the Hamiltonian as follows:

$$\begin{aligned} T_{i_1 i_N l_1 l_N;j_1 j_N k_1k_N} = \sum _{i_{TL},l_{TL},k_{TL}} V_{i_1 i_{TL} i_N ;l_1 l_{TL} l_N } \rho ^{TL}_{l_{TL};k_{TL}} V^+_{ k_1 k_{TL} k_N; j_1 i_{TL} j_N}, \end{aligned}$$

(35)

where the indexes with the subscript TL are the vector indexes of $(N-2)$ scalar binary indexes, for instance: $i_{TL} =\{ i_2\dots i_{N-1}\}$. We refer to these parameters as T-parameters. In formulas (34) and (35), we write the components of both the density matrices and the operator V, where both rows and columns are enumerated by the vector subscripts consisting of the binary indexes. For instance,

$$\begin{aligned} \rho ^{SR}_{i_1 i_N; j_1 j_N} \;\; {\text{ is } \text{ the } \text{ element } \text{ at } \text{ the } \text{ intersection } \text{ of } \text{ row }} \;\; \{i_1 i_N\} \;\; {\text{ and } \text{ column }} \;\; \{j_1 j_N\}, \end{aligned}$$

and similar for the components of the operator V.

If the transmission line is in ground state (2), then the expression for the T-parameters is simpler:

$$\begin{aligned} T_{i_1 i_N l_1 l_N;j_1 j_N k_1k_N} = \sum _{i_{TL}} V_{i_1 i_{TL} i_N ;l_1 0_{TL} l_N } V^+_{ k_1 0_{TL} k_N; j_1 i_{TL} j_N}, \end{aligned}$$

(36)

where $0_{TL} =(\underbrace{0,\dots ,0}_{N-2})$. The number of T-parameters is independent on the length of a transmission line and is completely defied by the dimensionality of the sender and receiver.

The T-parameters have two obvious symmetries. The first one follows from the Hermitian property of the density matrix (34), $(\rho ^{SR})^+=\rho ^{SR}$:

$$\begin{aligned} T_{i_1 i_N l_1 l_N; j_1j_N k_1 k_N} =T_{j_1j_N k_1 k_N;i_1 i_N l_1 l_N}^*\;\; \Rightarrow \;\; {\text{ Im }} \; T_{j_1j_N k_1 k_N;j_1 j_N k_1 k_N} =0. \end{aligned}$$

(37)

The second symmetry follows from the fact that these parameters must be symmetrical with respect to the exchange $S\leftrightarrow R$:

$$\begin{aligned} T_{i_1 i_N l_1 l_N; j_1j_N k_1 k_N} = T_{i_N i_1 l_N l_1; j_Nj_1 k_N k_1}. \end{aligned}$$

(38)

Finally, the set of T-parameters equals zero as a consequence of the fact that the Hamiltonian commutes with the z-projection of the total momentum $I_z$; therefore, the nonzero elements $V_{I,J}$ of the evolution operator are those, whose N-dimensional vector indexes I and J have equal number of units. Consequently (if the transmission line TL is in ground state (2) initially),

$$\begin{aligned} T_{i_1 i_N l_1 l_N; j_1j_N k_1 k_N} =0 \;\;{\text{ if }}\;\; \left\{ \begin{array}{l} i_1+i_N> l_1+l_N \\ j_1+j_N > k_1+k_N \\ i_1+i_N < l_1+l_N\;\;{\text{ and }}\;\; i_1+i_N -(j_1+j_N)\\ \ne l_1+l_N-(k_1+k_N) \end{array} \right. . \end{aligned}$$

(39)

In other words, the following T-parameters are nonzero:

$$\begin{aligned}&T_{i_1 i_N l_1 l_N; j_1j_N k_1 k_N} \ne 0 \;\;{\text{ if }}\;\;\nonumber \\&(i_1+i_N \le l_1+l_N) \wedge (j_1+j_N \le k_1+k_N)\nonumber \\&\wedge (i_1+i_N -j_1-j_N = l_1+l_N-k_1-k_N). \end{aligned}$$

(40)

The T-parameters are permanent characteristics of the communication line which do not change during its operation.

1.2 Explicit form for elements of receiver’s density matrix

We obtain the element of the receiver’s density matrix $\rho ^R(t)$ calculating the trace of the matrix $\rho ^{SR}$ (34) over the sender’s node:

$$\begin{aligned} \rho ^{R}_{i_N; j_N}=\sum _{i_1,j_1} \rho ^{SR}_{i_1 i_N; j_1 j_N} = T_{ i_N l_1;j_N k_1}\left( \rho ^S_0\right) _{l_1; k_1} , \end{aligned}$$

(41)

where

$$\begin{aligned} T_{ i_N l_1 ; j_N k_1}=\sum _{l_N,k_N,i_1} T_{i_1 i_N l_1 l_N;i_1 j_N k_1k_N}\left( \rho ^R_0\right) _{l_N; k_N}, \end{aligned}$$

(42)

and $T_{ i_N l_1 ; j_N k_1}$ satisfies the symmetry following from symmetry (37):

$$\begin{aligned} T_{ i_N l_1 ;j_N k_1 } =T_{j_N k_1;i_N l_1}^*\;\; \Rightarrow \;\; {\text{ Im }} \; T_{i_N l_1 ;i_N l_1 } =0. \end{aligned}$$

(43)

In result, the independent elements of $\rho ^R$ read as follows:

$$\begin{aligned} \rho ^{R}_{1;1}= & {} T_{1 0;1 0} +(T_{1 1;1 1}-T_{1 0;1 0}) x_1 +(T_{1 0;1 1} + T_{1 1;1 0}) x_2\nonumber \\&+i (T_{1 0;1 1} - T_{1 1;1 0}) x_3 ,\end{aligned}$$

(44)

$$\begin{aligned} \rho ^{R}_{0;1}= & {} T_{0 0;1 0} +(T_{0 1;1 1}-T_{0 0;1 0}) x_1 +(T_{0 0;1 1} + T_{0 1;1 0}) x_2\nonumber \\&+i (T_{0 0;1 1} - T_{0 1;1 0}) x_3, \end{aligned}$$

(45)

which is a system of linear algebraic equations allowing us to determine the initial parameters $x_i$ knowing the registered density matrix of the receiver’s state. We can conveniently rewrite system (44) separating the real and imaginary parts to get three independent real equations (17).

1.3 Some properties of determinants

The both determinants $\Delta ^{(1)}$ and $\Delta ^{(2)}$ depend on the parameters of the initial states of the sender and receiver: $\lambda ^S$, $\lambda ^R$, $\alpha _i$, $\beta _i$, $i=1,2$. But this dependence is partially separated, which has been already used in eqs.(21): expressions $\left| \frac{\partial (y_i,y_j)}{\partial (x_n,x_m)}\right|$ and $\left| \frac{\partial y_i}{\partial x_n}\right|$ in, respectively, eqs.(18) and (19) depend on $\lambda ^R$, $\beta _i$, $i=1,2$, while expressions $\left| \frac{\partial (x_n ,x_m)}{\partial (\alpha _1,\alpha _2)}\right|$ and $\left( \left| \frac{\partial x_n }{\partial \alpha _1} \right| + \left| \frac{\partial x_n }{\partial \alpha _2} \right| \right)$ in, respectively, eqs.(18) and (19) depend on $\lambda ^S$, $\alpha _i$, $i=1,2$. All this immediately follows from the definitions of $x_i$ (16) and elements of $\rho ^R$ (17).

Notice that each term in definitions (19) and (18) is the independent determinant condition for solvability of system (17) for, respectively, two parameters $\alpha _i$, $i=1,2$, or one of them. In other words, if there are k nonzero terms in these formulas, then we can find parameters $\alpha _i$ ($i=1,2$) in k different ways. In principle, if each term is small in eq.(18) (or (19)), then the parameters $\alpha _1$ and $\alpha _2$ (or one of them) can be found from system (17) with restricted accuracy. However, if there are k small but nonzero terms in (19) (or (18)), then the accuracy can be improved by calculating the transferred parameters k times and comparing the results. For this reason, we do not divide the sums in both formulas (19) and (18) by the number of terms in them.

1.4 Choice of time instant for state registration

Now we show that C and the determinants $\Delta ^{(i)}$ averaged over the initial conditions are maximal at the time instant of the maximum of $\langle {\bar{P}}\rangle _{\lambda ^S,\lambda ^R}(t) = {\bar{P}}(t)$, where

$$\begin{aligned} {{\bar{P}}}(t)\equiv & {} \langle P\rangle _{{\tilde{\Gamma }}}= \frac{1}{P_0}\left\langle \rho ^{(SR)}_{01;01} (t)+ \rho ^{(SR)}_{10;10} (t)+ \rho ^{(SR)}_{11;11}(t)\right\rangle _{{\tilde{\Gamma }}}=\nonumber \\&\frac{2}{3}\left( T_{0110;0110}(t) +T_{1010;1010}(t)+ T_{1011;1011}(t) + \frac{1}{2}T_{1111;1111}(t) \right) . \end{aligned}$$

(46)

Here $P_0=\frac{3}{4}$ is the normalization fixed by the requirement ${{\bar{P}}}|_{t=0}=1$ and we take into account that ${{\bar{P}}}$ does not depend on the initial eigenvalues $\lambda ^S$ and $\lambda ^R$. The function P can be viewed as a probability of registration of the excitation at the nodes of the subsystem SR. The numerical calculations show that its maximum coincides with the maximum of fidelity of a one-qubit pure state transfer:

$$\begin{aligned} {{\bar{P}}}^R(t)= \rho ^{(SR)}_{01;01}(t)|_{ \Gamma =\{0,1,0,0,0,0\}}= T_{0110;0110}(t) . \end{aligned}$$

(47)

This fact simplifies our calculations.

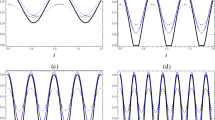
The time dependences of the functions $\langle {\bar{P}}\rangle _{\lambda ^S,\lambda ^R}\equiv {\bar{P}}$, $\langle \bar{\Delta }^{(i)} \rangle _{\lambda ^S,\lambda ^R}$ and $\langle {{\bar{C}}} \rangle _{\lambda ^S,\lambda ^R}$ are shown in Fig. 10 for the chain of $N=40$ nodes (for convenience, we normalize them by their maxima over the considered long enough interval, $0\le t \le 50$ , i.e., we show the ratios

$$\begin{aligned} \langle {P} \rangle _n= \frac{\langle {\bar{P}} \rangle _{\lambda ^S,\lambda ^R}}{ \langle {\bar{P}} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}},\;\; \langle {C} \rangle _n= \frac{\langle {\bar{C}} \rangle _{\lambda ^S,\lambda ^R}}{ \langle {\bar{C}} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}},\;\; \langle {\Delta }^{(i)} \rangle _n=\frac{\langle \bar{\Delta }^{(i)} \rangle _{\lambda ^S,\lambda ^R}}{ \langle \bar{\Delta }^{(i)} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}}, \end{aligned}$$

(48)

where

$$\begin{aligned} \langle {\bar{P}} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}= & {} \langle {\bar{P}} \rangle _{\lambda ^S,\lambda ^R}|_{t=43.442}=0.5476,\;\; \langle {\bar{C}} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}=\langle {\bar{C}} \rangle _{\lambda ^S,\lambda ^R}|_{t=43.442}=9.584\times 10^{-3},\nonumber \\ \langle \bar{\Delta }^{(2)} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}= & {} \langle \bar{\Delta }^{(2)} \rangle _{\lambda ^S,\lambda ^R}|_{t=43.442}=9.846\times 10^{-2},\;\; \langle \bar{\Delta }^{(1)} \rangle _{\lambda ^S,\lambda ^R}^\mathrm{max}\nonumber \\= & {} \langle \bar{\Delta }^{(1)} \rangle _{\lambda ^S,\lambda ^R}|_{t=43.442}=0.2765. \end{aligned}$$

(49)

Fig. 10

The time-dependence of the normalized mean probability $\langle {\bar{P}}\rangle _{n}$ (dotted line), mean SR-concurrence $\langle {\bar{C}} \rangle _{n}$ (solid line), mean determinants $\langle \bar{\Delta }^{(2)} \rangle _{n}$ (dash-dotted line) and $\langle \bar{\Delta }^{(1)} \rangle _{n}$ (dashed line) defined in eq.(48) with normalizations given in (49). All four curves have the maximum at the same time instant $t=43.442$ (we use the values of T-parameters found in “Numerical values of T-parameters for $N = 40$ at optimized time instant” section of Appendix

We see that the time instant of the maxima is the same for all four functions and equals $t=43.442$. Namely this optimized time instant is taken for our calculations.

1.5 Numerical values of T-parameters for $N=40$ at optimized time instant

For the case $N=40$, we have calculated the T-parameters at the optimized time instant $t=43.442$ found in “Choice of time instant for state registration” section of Appendix. Similar to [38], the T-parameters can be separated into three families by their absolute values. We give the list of these families up to symmetries (37,38).

1st family: There are two different parameters with the absolute values gapped in the interval $[6.817\times 10^{-1},1]$:

$$\begin{aligned} T_{0000;0000}=1, T_{0000;0110}=-6.817 i \times 10^{-1}. \end{aligned}$$

(50)

2nd family: There are 8 different parameters with the absolute values gapped in the interval $[2.160\times 10^{-1} ,5.353\times 10^{-1} ]$:

$$\begin{aligned}&T_{0001;0001}=5.352 \times 10^{-1} ,\;\; T_{0 0 1 1;0 0 1 1}= 2.865 \times 10^{-1},\;\;\nonumber \\&T_{0 0 0 1;0 1 1 1}= 3.649 i \times 10^{-1},\;\; T_{0 0 0 0;1 1 1 1}= 4.648 \times 10^{-1},\;\;\nonumber \\&T_{0 1 1 0;0 1 1 0}= 4.648 \times 10^{-1},\;\; T_{0 1 1 1;0 1 1 1}= 2.488 \times 10^{-1} ,\;\;\nonumber \\&T_{0 1 1 0;1 1 1 1}= 3.169 i \times 10^{-1},\;\; T_{1 1 1 1;1 1 1 1}= 2.160 \times 10^{-1}. \end{aligned}$$

(51)

3rd family: There are 5 different parameters with the absolute values gapped in the interval $[0,5.396 \times 10^{-3}]$:

$$\begin{aligned}&T_{0 0 0 0;0 1 0 1}= -5.395 \times 10^{-3}, \;\; T_{0 0 1 0;0 1 1 1}= -2.888 \times 10^{-3},\nonumber \\&T_{0 1 0 1;0 1 0 1}= 2.911 \times 10^{-5},\;\; T_{0 1 0 1;0 1 1 0}= 3.678 i \times 10^{-3},\nonumber \\&T_{0 1 0 1;1 1 1 1}= -2.508 \times 10^{-3}. \end{aligned}$$

(52)

Notice that the parameter $T_{0001;0010}$ vanishes only due to the nearest-neighbor interaction model and/or even N. It becomes non-vanishing if at least one of these conditions is destroyed.

We see that there are certain gaps between the neighboring families, which is most significant ($\sim 10^2$) between the 2nd and the 3rd families. In addition, the parameters from the 3rd family are smallest ones. Similar to ref. [38], this difference in absolute values of the T-parameters is due to the symmetries of transitions among the different nodes of the chain. The obtained values of the T-parameters are used in Sect. 4.2.