Efficient quantum state transfer in an engineered chain of quantum bits

Abstract

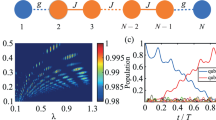
We present a method of performing quantum state transfer in a chain of superconducting quantum bits. Our protocol is based on engineering the energy levels of the qubits in the chain and tuning them all simultaneously with an external flux bias. The system is designed to allow sequential adiabatic state transfers, resulting in on-demand quantum state transfer from one end of the chain to the other. Numerical simulations of the master equation using realistic parameters for capacitive nearest-neighbor coupling, energy relaxation, and dephasing show that fast, high-fidelity state transfer should be feasible using this method.

Appendix

Here we derive our expressions for nearest-neighbor coupling of the transmon qubits. We start from the circuit shown in Fig. 1b. The input and output terminals are the points that connect the Josephson junctions ($J_1$ and $J_2$) to the circuit. We select $J_1$ to be the input and $J_2$ the output. We remove the shunting capacitances $C_{12}$ and $C_{34}$, since these can be viewed as part of the source (load) impedance and concentrate on the coupling network. The equivalent open output voltage $V_\mathrm{out}^T$ is given by the expression

$$\begin{aligned} V_\mathrm{out}^T=\frac{C_{13}C_{24}-C_{14}C_{23}}{(C_{13}+C_{23}) (C_{14}+C_{24})}V_\mathrm{in}. \end{aligned}$$

(8)

We then short circuit the output and calculate the shorting current

$$\begin{aligned} I_s=\frac{V_\mathrm{in}i\omega (C_{13}C_{24}-C_{23}C_{14} )}{C_{13}+C_{23}+C_{14}+C_{24}}. \end{aligned}$$

(9)

Instead of rewriting the source voltage as $V_\mathrm{out}^T$ as is done in the standard Thevenin equivalent we follow the example in appendix A of Ref. [15] and introduce a shunt capacitance $\tilde{C}_{B2}$ to the output and keep the source voltage to be $V_\mathrm{in}$. The circuit now consists of a source at voltage $V_\mathrm{in}$, an impedance in series with the source and a shunt impedance, parallel with the output. The series impedance gives the condition

$$\begin{aligned} Z_\mathrm{in}=\frac{V_\mathrm{in}}{I_s}=\frac{1}{i\omega C_\mathrm{in}}=\frac{C_{13}+C_{14}+C_{23}+C_{24}}{i\omega (C_{13}C_{24}-C_{14}C_{23})}. \end{aligned}$$

(10)

We then find the shunt impedance from voltage division by requiring that across the shunt impedance should be $V_\mathrm{out}$ derived above. This gives an expression for a shunt capacitance $\tilde{C}_{B2}$:

$$\begin{aligned} \tilde{C}_{B2}=\frac{C_{13}C_{14}+2C_{14}C_{23}+ C_{23}C_{24}}{C_{13}+C_{14}+C_{23}+C_{24}}. \end{aligned}$$

(11)

Changing the input and output sides we can also introduce a shunt capacitance on the input $\tilde{C}_{B1}$. We define new shunt capacitance by reintroducing the source (load) capacitance $C_{12}$ ($C_{34}$) so that $C_{B1}=\tilde{C}_{B1}+C_{12}$ and $C_{B2}=\tilde{C}_{B2}+C_{34}$. The capacitive network now consists of three capacitances $C_\mathrm{in}$, $C_{B1}$ and $C_{B2}$ in a $\pi$- circuit. We now introduce the node fluxes $\varPhi _1$ and $\varPhi _2$ at the each side of the coupling capacitance $C_c$ branch. As a first step in quantizing the circuit (see Ref. [6]) we write down the Lagrangian:

$$\begin{aligned} \mathscr {L}= & {} \frac{C_{B1}\dot{\varPhi }_1^2}{2}+ \frac{C_{B2}\dot{\varPhi }_2^2}{2}+\frac{C_{c}(\dot{\varPhi }_2- \dot{\varPhi }_1)^2}{2}+E_{J1}\cos (2\pi \varPhi _1/\varPhi _0)\nonumber \\&+\,E_{J2}\cos (2\pi \varPhi _2/\varPhi _0). \end{aligned}$$

(12)

We then get the classical Hamiltonian through the standard Legendre transformation by expressing $\dot{\varPhi }_1$ and $\dot{\varPhi }_2$ as

$$\begin{aligned} \dot{\varPhi }_1=\frac{(C_{c}+C_{B2})p_1+C_cp_2}{C_cC_{B1}+C_cC_{B2}+C_{B1}C_{B2}} \end{aligned}$$

(13)

$$\begin{aligned} \dot{\varPhi }_2=\frac{(C_{c}+C_{B2})p_2+C_cp_1}{C_cC_{B1}+C_cC_{B2}+C_{B1}C_{B2}} \end{aligned}$$

(14)

where $p_1$ and $p_2$ are the canonical momentum:

$$\begin{aligned} p_1=\frac{\partial \mathscr {L}}{\partial \dot{\varPhi }_1} \end{aligned}$$

(15)

$$\begin{aligned} p_2=\frac{\partial \mathscr {L}}{\partial \dot{\varPhi }_2}. \end{aligned}$$

(16)

To get the quantum mechanical Hamiltonian we replace $\varPhi _{1,2}$ and $p_{1,2}$ with the quantum mechanical operators $\hat{\varPhi }_{1,2}$ and $\hat{p}_{1,2}$ that obey the commutation relations

$$\begin{aligned}{}[\hat{\varPhi }_n,\hat{p}_m]=i\delta _{n,m}\left( \frac{\varPhi _0}{2\pi }\right) \end{aligned}$$

(17)

where $\delta _{n,m}$ is Kronecker’s delta. We now introduce the Cooper-pair number operator defined as $\hat{n}_i=\hat{p}_i/2\mathrm {e}$. This allows us to write down the Hamiltonian shown in Eq. 2. In that expression we have defined the charging energies $E_{CC}$, $E_{C1}$ and $E_{C2}$ in the re-normalized capacitances:

$$\begin{aligned} C_{ec}= & {} \frac{(C_{B1}C_{B2}+C_{B1}C_{c}+C_{B2}C_{c})^2}{C_{c}^2(C_{B1}+C_{B2})} \end{aligned}$$

(18)

$$\begin{aligned} C_{e1}= & {} \frac{(C_{B1}C_{B2}+C_{B1}C_{c}+C_{B2}C_{c})^2}{(C_{B1}C_{B2}C_{c}+ C_{B2}^2C_{c}+0.5(C_{B1}C_{B2}^2+C_{B1}C_{c}^2+C_{B2}C_{c}^2))} \end{aligned}$$

(19)

$$\begin{aligned} C_{e2}= & {} \frac{(C_{B1}C_{B2}+C_{B1}C_{c}+C_{B2}C_{c})^2}{(C_{B1}C_{B2} C_{c}+C_{B1}^2C_{c}+0.5(C_{B1}^2C_{B2}+C_{B1}C_{c}^2+C_{B2}C_{c}^2))}. \end{aligned}$$

(20)

obtained by collecting the terms for $\hat{n}_1\hat{n}_2$, $\hat{n}_1^2$ and $\hat{n}_2^2$, respectively. We see that if we let $C_c \rightarrow 0$ we retain the expression for two uncoupled transmon qubits. These expressions can in the same manner be extended to the case where each qubit has two nearest neighbors.