Modeling of HOT (111) HgCdTe MWIR detector for fast response operation

Abstract

The paper reports on photoelectrical performance of the mid-wave infrared (MWIR) (111) HgCdTe high operating temperature detector for the fast response conditions. Detector structure was simulated with software APSYS by Crosslight Inc. The detailed analysis of the time response as a function of device architecture and applied voltage was performed pointing out optimal working conditions. The time response of the MWIR HgCdTe detector with 50 % cut-off wavelength of $\lambda _{c} \approx 5.3\, \upmu \hbox {m}$ at $T = 200$ K was estimated at the level of $\tau _{s} \approx$ 2,500 ps for $V = 100$ mV and series resistance $R_{Series} = 510\,\Omega$. The series resistance’s reduction enables to reach $\tau _{s}\approx 60\!-\!500$ ps.

1 Introduction

Higher operation temperature (HOT) condition of the mid-wave (3–8 $\upmu \hbox {m}$) photodetectors is one of the most important research areas in infrared technology (Martyniuk and Rogalski 2013). The development of the new detector architectures has been driven by applications requiring fast response operation. This requirement stays in contradiction with reaching high detectivity in terms of detector optimization. Two methods to reach a short response time of the detectors may be listed: high recombination decay in absorber region and fast transport of the photogenerated carriers to contacts. The recombination mechanism is important for forward and weak reverse conditions, while carrier transport is significant for higher reverse voltage. Except of voltage, the drift time strongly depends on thickness of the absorption region. Reducing the thickness of the active region, the short drift times could be reached, but this is not a proper solution to improve the response time of detector because, devices with thin active regions lead to poor quantum efficiency and lower detectivity. Additionally, Hu et al. calculated optimal thickness of absorption layer versus absorption and diffusion lengths showing its dependence on incident light wavelength and minority carrier lifetimes (Hu et al. 2008). In this case, a special heterostructure designs are developed, where $p$-type absorber is advantageous due to both high diffusion and drift ambipolar mobility, what is consider as a must to achieve fast and efficient collection of charge carriers. Additionally, in the fundamental approach, $p$-type HgCdTe active regions are characterized by the best compromise between obligation of the high quantum efficiency and a low thermal generation driven by the Auger 7 generation-recombination (GR) mechanism (Piotrowski and Rogalski 2007).

In general, most of photodiodes with short time response are based on heterostructures to prevent from parasitic thermal generation at contacts (Ashley and Elliott 1985). A complex multi-layer structure in which the transport of majority and minority carriers is determined by barriers has been used with great success in our laboratory for MWIR photodiodes operating at HOT conditions. The main modification in comparison with the standard three-layer $\hbox {N}^{+}{\uppi } \hbox {P}^{+}$ structure invented for non-equilibrium conditions is programmed grading of band gap and doping level at heterojunctions (interfaces) (Elliot et al. 1996; Piotrowski et al. 2007a, 2009, 2010).

In this paper we present the theoretical modeling of the photodetector for fast response conditions based on epitaxial HgCdTe multi-layer graded gap architecture. Detector structure was characterized and simulated with software APSYS by Crosslight Inc. The voltage and structural dependence of the dark current and time response characteristics including both trap-assisted (TAT) and band-to-band (BTB) tunneling mechanisms at the graded heterojunctions were simulated. The time response of the MWIR HgCdTe detector with 50 % cut-off wavelength of $\lambda _{c} \approx 5.3\,\upmu \hbox {m}$ at $T = 200$ K was estimated at the level of $\tau _{s} \approx \hbox {2,500}$ ps for $V = 100\,\hbox {mV}\,(R_{Series} = 510\,\Omega )$. Dark current was found to be driven mostly by TAT/BTB mechanism reaching $\approx 0.2\,\hbox {A/cm}^{2}$ at 1,500 mV.

2 Simulation procedure

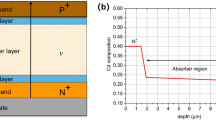
The device presented in this paper was fabricated in the joint laboratory run by Vigo Systems and Military University of Technology (MUT). The (111) HgCdTe layers were grown on 2” in., epiready, semi-insulating (100) GaAs substrates in a horizontal MOCVD AIX 200 reactor. The interdiffused multilayer process (IMP) technique was applied for the HgCdTe layer’s deposition. The $\hbox {N}^{+}\uppi \hbox {P}^{+}$ structure has been expanded with interfaces 1/2/3, where interface 3 (layers 13/14/15-$\hbox {p}^{+}$-$\hbox {n}^{+}$) plays a role of the tunneling graded gap junction improving contact properties to the $\hbox {P}^{+}$ barrier layer (Fig. 1). The detailed description of the multi-layer HgCdTe detector growth and fabrication procedures could be found in previous paper (Piotrowski et al. 2007b). It is believed that response time of the presented structure may be improved by optimization of the both interfaces 1 and 3 and implementation of the TAT mechanism especially at interface 3. Interface layers were assumed to be $x$-graded regions and represent the real structure which profile was shaped using interdiffusion processes during HgCdTe growth.

Fig. 1

Simulated graded gap HgCdTe heterostructure. The layer number, type of doping, composition grading, doping grading $\times 10^{16 }\hbox {cm}^{-3}$, and thickness of the layers in $\upmu \hbox {m}$ are marked. Red arrow presents composition and doping grading. (Color figure online)

Theoretical modeling of the HgCdTe heterostructures has been performed by numerical solving of Poisson’s and the electron/hole current continuity equations. The commercially available APSYS platform (Crosslight Inc.) was implemented in our simulation procedure. APSYS uses the Newton-Richardson method of nonlinear iterations. The applied model incorporates both HgCdTe electrical and optical properties to estimate device performance taking into consideration radiative (RAD), Auger (AUG), Shockley Read-Hall (SRH) GR and BTB as well as TAT tunneling mechanisms. In TAT simulation the Hurkx et al. model was implemented (Hurkx et al. 1992). The TAT mechanism was found to be important by assuming trap concentration $N_{Trap} = 10^{10}\,\hbox {cm}^{-3}$ at the tunneling interfaces 1 and 3. The absorption was only assumed in active layer region. The HgCdTe absorption coefficient was estimated according to Kane model including its composition, doping and temperature dependence $(\alpha = \hbox {3,390}\,\hbox {cm}^{-1}, \lambda _{c} = 5.3\,\upmu \hbox {m}, T = 200\,\hbox {K})$.

It must be stressed that HgCdTe is a narrow-gap semiconductor that exhibits a non-parabolic conduction band and high carrier degeneracy. These conditions are very difficult to fulfil because of numerical problems with computation of the Fermi-Dirac integral for non-parabolic model. Quan et al. and Wang et al. have proposed approximations to this expression, however mentioned solution have only been validated for $T = 77\!-\!120\,\hbox {K}$ (Quan et al. 2007a, b; Wang et al. 2010, 2011). Since HgCdTe device studied in this work operates at increased temperatures 200 K and proposed approximations has not been fully validated for HOT conditions yet, computations were performed using the Fermi-Dirac statistics for a non-degenerate semiconductor model with parabolic energy bands. Such simplification gives quite good results in a broad range doping concentrations (Wenus et al. 2001).

The specific equations describing drift-diffusion (D-D) model and HgCdTe parameters used in calculation of recombination rates are described in detail in Capper’s monograph, APSYS manual and Table 1 (Capper 1994; APSYS 2011). Analysis of high frequency behavior of a semiconductor device was performed using Li and Dutton model (Li and Dutton 1991).

Table 1 Parameters taken in modeling of MWIR HgCdTe heterostructure

3 Simulation results

Assuming abrupt heterojunctions in simulated heterostructure, the discontinuities of both conduction and valence bands may be visible. This could have adverse effect on device properties contributing to spikes in charge carriers concentration, thermal generation rates and electric field. The consequence of this effect is a large dark current due to the thermal generation and tunneling mechanisms. As mentioned above, the possible solution is programmed grading of band gap and doping level at heterojunctions (interfaces 1/3). Band diagram of the simulated structure at $V = 300\,\hbox {mV}$ is shown in Fig. 2a. Two heterojunctions (interfaces 1/3, refer to Fig. 1) were found to be decisive as for as photoelectrical performance is concerned. Having assumed interface 3 $x = 0.15$, the applied voltage drops mostly on the interface 1 (layer 3/4), while interface 3 is forwardly biased which was presented in Fig. 2b. Situation changes for higher compositions. In this case, for interface 3 $x = 0.35$, the voltage drops on both interfaces reducing electric field at interface 3 and increasing at interface 1, respectively. The proper optimization of the both interfaces 1/3 seems to be considered as the most important step in detector simulation in terms of fast response time operation.

Fig. 2

Simulated band diagram of graded gap HgCdTe heterostructure (a); electric field along the sample for selected voltage for interface $x = 0.15$ (b) and $x = 0.35$ (c). (Color figure online)

Figure 3 presents $J_{DARK}$ versus applied voltage. In low range of bias, the $J_{DARK}$ characteristic was fitted to the measured one by SRH GR mechanism in absorber region. For $V > 250$ mV, the dark current density is mostly driven by TAT and BTB on interface 1 (see Fig. 3; for interface 3 $x = 0.15$, compare TAT/BTB interface 1/3 and TAT/BTB interface 1). The characteristic carrier TAT lifetimes in Hurks et al. model was assumed to be equivalent to SRH lifetimes. Green dashed line presents $J_{DARK}$ without influence of tunneling mechanism at interfaces 1 and 3. The energy band gap of the layers 13/14/15 (interface 3) $\approx$ 0.041 eV for $x = 0.15$ and $T = 200\,\hbox {K}$, which means that under proper voltage, the TAT mechanism should improve time response characteristics. Situation changes when composition of the layers 13/14/15 increases to 0.35, when the hole transport to the left contact may be disturbed in the low bias range ($<$250 mV) by higher energy gap at the interface 3 reducing $J_{DARK}$ by nearly two orders of magnitude (see dashed navy line in Fig. 3).

Fig. 3

Measured and simulated dark current density versus voltage for selected interface 3 composition. (Color figure online)

Measured and simulated time response characteristic versus voltage for $T = 200\,\hbox {K}$ are presented in Fig. 4. The fitting to the experimental result was reached with the series resistance $R_{Series} = 510\,\Omega$ attached to the detector’s structure. The time response was measured with optical parametric oscillator (OPO) producing 25 ps pulses of tunable wavelengths in range of 1.55–16 $\upmu \hbox {m}$. The detailed description of the measurement procedure may be found in previous paper (Stanaszek et al. 2009). Theoretical simulation also assumed 25 ps pulses and wavelength $\lambda = 5\,\upmu \hbox {m}$, respectively. Time response was estimated from exponential decay of the photocurrent ($J_{PHOTO}$) versus time. The proper correspondence with experimental results was reached in the range $<$300 mV. It is believed that series resistance exhibits non-linear behavior versus voltage. For lower voltages the drift influence is reduced and $\tau _{s}$ is determined mostly by recombination decay and ambipolar diffusion of photogenerated carriers to the contact region. Once the voltage increases, the drift component starts to dominate. The carriers lifetime driven by AUG 7 and SRH recombination mechanisms for average active layer composition $x \approx 0.265$ was found to be at level $\tau _{A7} \approx 6\,\upmu \hbox {s}$ and $\tau _{SRH} \approx 0.3\,\upmu \hbox {s}$, respectively (for $N_{A}= 5\times 10^{15}\,\hbox {cm}^{-3}, N_{Trap} = 10^{13}\,\hbox {cm}^{-3}$ and $\sigma _{n}=\sigma _{p} = 5 \times 10^{-15}\,\hbox {cm}^{-2})$, while at the interface 3 for $x = 0.15$ AUG 7 and SRH times were estimated at the level $\tau _{A7} = 3\,\hbox {ns}; \tau _{SRH} = 100$ and $0.1\,\upmu \hbox {s}$ (for $N_{Trap} = 10^{10}\,\hbox {cm}^{-3}$; $10^{13}\,\hbox {cm}^{-3}$, respectively). Ambipolar diffusion time was estimated to be $\sim 2$ ns and drift time $(V = 500\,\hbox {mV})$ were found at the level of $\sim 140$ ps for active layer. The absorber layer was assumed to be $p$-type doped to meet the requirement of $N_{A} \approx 2\,n_{i}$ ($n_{i}$-intrinsic concentration) to reach the highest detectivity (fundamental limitation by intrinsic AUG 7 GR process), while absorber width was assumed to be slightly higher than $1/\alpha$ in order not to influence quantum efficiency.

Fig. 4

Measured and simulated time response versus voltage. (Color figure online)

Interface 3 (layer 13/14/15) should be optimized by proper choice of composition and doping. Time response dependence on layer 13/14/15 composition is presented in Fig. 5a for TAT/BTB processes assumed at interface 3; BTB assumed at interface 1/3 (Fig. 5b) and different $R_{Series} = 0/510\,\Omega$, respectively. Assuming no $R_{Series}$ influence (Fig. 5a), the conduction/valence band offset at interface 3 and voltage drop on both interfaces 1/3 must be taken into consideration (see Fig. 2b, c). The higher voltage drops on both interfaces 1/3 in comparison with the structure with $R_{Series}$ included. Once interface 3 composition increases, the time response decreases reaching its minimal value being dependent on applied voltage, assumed trap concentration and trap energy levels within bandgap. As we moving to the higher interface 3 compositions, the higher electric field drops on interface 3 (see Fig. 2c) lowering the capabilities of the interface 1, which is responsible for the electron hole separation. In addition, the recombination time increases at the interface 3 (for higher $x$) resulting in rising of time response. Assuming only BTB mechanism at both interfaces during simulations, $\tau _{s}$ is higher in comparison with the case when TAT/BTB mechanisms are incorporated at interface 3.

Fig. 5

Time response versus interface 3 $x$ for $V = 200/300\,\hbox {mV}; R_{Series} = 0$ (a) and $R_{Series} = 510$ $\Omega$ (b). (Color figure online)

Figure 6a and b present theoretical dependence of the photocurrent for selected interface 3 compositions for two modelled voltages 100 and 300 mV $(R_{Series} = 0\,\Omega )$. As expected the response is enhanced at higher applied reverse bias to the certain level of interface 3 composition $(x \approx 0.3)$, what fully confirms dominant influence of both ambipolar diffusion and drift mechanisms on response time of simulated detector.

Fig. 6

Theoretical dependence of photocurrent versus time for selected interface 3 $x$ and voltage 100 (a) and 300 mV (b). (Color figure online)

The time response dependence on the layer 14/15 doping simulated for selected $R_{Series}$ is shown in Fig. 7. Assuming, the structure without $R_{Series}$ and high doping in layer 14/15, the simulated structure enables to reach $\tau _{s} \approx 500$  ps. For low doping $< 5\times 10^{15} \hbox {cm}^{-3}, \tau _{s}$ slightly increases for every analyzed series resistance. As a reference, the differential resistance area product ($R_{0}A$) of the typical photodiodes designed and fabricated at MUT/Vigo Systems laboratory and optimized for $\lambda _{c} = 5.3\,\upmu \hbox {m}$ ranges from 0.2–1 $\Omega \,\hbox {cm}^{2}$.

Fig. 7

Time response versus doping of the layer 14 and 15 (see Fig. 1) for $V = 300\,\hbox {mV}$. (Color figure online)

The influence of TAT/BTB mechanism on time response was presented in Fig. 8 for interface 3 $x = 0.15; R_{Series} = 0$ (a) and 510 $\Omega$ (b), respectively. The characteristic lifetimes at the trap levels was assumed to be equivalent to SRH lifetimes used in $J_{DARK}$ and $\tau _{s}$ fitting presented in Fig. 3 and 4. Assuming TAT/BTB at the Interface 3 ($R_{Series} = 0\,\Omega$) the influence of the tunneling mechanism is desirable (dotted blue line) reaching the best time response conditions. TAT/BTB at interface 1 is considered to have adverse influence on performance of the detector. Attaching $R_{Series} = 510\,\Omega$ to the detector structure, the highest $\tau _{s}$ could be obtained for TAT/BTB at interface 1 which is connected with changes of the electric field on particular interfaces. Similar considerations for interface 3 $x = 0.35$ are presented in Fig. 9a and b, respectively. Theoretical simulations indicate that for ideal conditions $(R_{Series} = 0\,\Omega )$ the best $\tau _{s} \approx$ 60 ps may be reached in low bias region $<$250 mV.

Fig. 8

Influence of tunneling mechanism on time response at interface 1 and 3 for interface 3 $x = 0.15$ and $R_{Series} = 0$ (a) and 510 $\Omega$ (b). (Color figure online)

Fig. 9

Influence of tunneling mechanism on time response at interface 1 and 3 for interface 3 $x = 0.35$ and $R_{Series} = 0$ (a) and 510 $\Omega$ (b). (Color figure online)

4 Conclusion

The time response characteristics were theoretically simulated showing its TAT/BTB and $R_{Series}$ dependence. The proper fitting to the experimental results was achieved using the presented models. The appropriate controlling of $R_{Series}$ (detector processing) and the tunneling effects at interface 1 and 3 allows to decrease the $\tau _{s}$ below 500 ps. Theoretical simulations indicates that assuming proper TAT/BTB mechanism and $R_{Series}$ the shorter response times could be obtained even for interfaces’ composition higher than nominal, assumed in growth procedure.