Analysis of Schwarz waveform relaxation for the coupled Ekman boundary layer problem with continuously variable coefficients

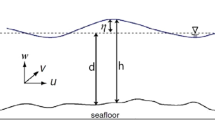
Abstract

In this paper, we present a global-in-time non-overlapping Schwarz method applied to the Ekman boundary layer problem. Such a coupled problem is representative of large-scale atmospheric and oceanic flows in the vicinity of the air-sea interface. Schwarz waveform relaxation (SWR) algorithms provide attractive methods for ensuring a “tight coupling” between the ocean and the atmosphere. However, the convergence study of such algorithms in this context raises a number of challenges. Numerous convergence studies of Schwarz methods have been carried out in idealized settings, but the underlying assumptions to make these studies tractable may prohibit them to be directly extended to the complexity of climate models. We illustrate this aspect on the coupled Ekman problem, which includes several essential features inherent to climate modeling while being simple enough for analytical results to be derived. We investigate its well-posedness and derive an appropriate SWR algorithm. Sufficient conditions for ensuring its convergence for different viscosity profiles are then established. Finally, we illustrate the relevance of our theoretical analysis with numerical results and suggest ways to improve the computational cost of the coupling. Our study emphasizes the fact that the convergence properties can be highly sensitive to some model characteristics such as the geometry of the problem and the use of continuously variable viscosity coefficients.

Appendices

Appendix:

Quadratic viscosity basis functions

Equation (12a) using the quadratic viscosity ν(z) = c + bz + az² for z ∈Ω, can be reduced to the Legendre ODE $\displaystyle \left (1 - \eta ^{2} \right ) \frac {\textup {d}^{2} y}{\textup {d} \eta ^{2}} - 2 \eta \frac {\textup {d} y }{\textup {d} \eta } + \xi \left (\xi + 1 \right ) y = 0$ with

$$ \eta\left( z \right) = \frac{2a}{\sqrt{b^{2}-4ac}} \left( z+\frac{b}{2a} \right) \quad\text{ and}\quad \xi = -\frac{1}{2} \left( 1 \pm \sqrt{1+ \frac{4 \imath \left( f + \omega \right)}{a}} \right), $$

(64)

where the choice of the sign in (64) does not bear any consequence. In particular, one can show that using relevant quadratic viscosity functions, (e.g. satisfying ν(z) > 0 for all z ∈Ω and $(a,b,c) \in \mathbb {R}_{-}^{*} \times \mathbb {R}^{2}$), $\eta \in \mathbb {R}$ and satisfies − 1 < η(z) < 1 for z ∈Ω. The functions given by (32a) are then numerically satisfactory solutions to the Legendre ODE [meaning that computing a reasonable amount of sum terms leads to accurate values, [38]], and thus to (12a). In our numerical results, Legendre functions have been computed using the hypergeometric function ₂F₁ [33] through: $\displaystyle P_{\xi }^{0} \left (\eta \right ) = {}_{2} F_{1}\left (\xi +1, -\xi , 1; \eta \right )$.

On the observed discretized convergence factor

Let us consider the numerical solution of the coupled problem (3a) on a given time window $\mathcal {T}_{n}$ using a finite difference discretization in time. The observed error can be written as (with U_j = (u_j,v_j)):

$$ \mathbf{E}_{j}^{k,m}(z) = \mathbf{U}_{j}^{k,m}(z) - \mathbf{U}_{j}(z,{t^{m}_{j}}) 1 \leq m \leq M_{j}, j \in \{1,2\}, k \in \mathbb{N}^{*}, $$

(65)

where m is an index for the time step, ${t^{m}_{j}}$ is the physical time corresponding to time step m, and M_j is the total number of time steps for the numerical approximation of U_j in $\mathcal {T}_{n}$. A convergence rate characterizing the behaviour of $\mathbf {E}_{j}^{k,m} = (E_{u,j}^{k,m},E_{v,j}^{k,m} )$ as a function of k is:

$$ \mathcal{R}_{\mathbf{U}_{j}}^{k} = \frac{ \left\| \left( \mathbf{E}_{j}^{k,m}(0^{\mp})\right)_{m} \right \|_{2}} { \left\| \left( \mathbf{E}_{j}^{k-1,m}(0^{\mp})\right)_{m} \right \|_{2}} = \frac{\left[ \underset{m=1}{\overset{M_{j}}{\sum}} \left( \left( {E}_{u,j}^{k,m}(0^{\mp})\right)^{2} + \left( {E}_{v,j}^{k,m}(0^{\mp})\right)^{2} \right) \right]^{1/2}} {\left[ \underset{m=1}{\overset{M_{j}}{\sum}} \left( \left( {E}_{u,j}^{k-1,m}(0^{\mp})\right)^{2} + \left( {E}_{v,j}^{k-1,m}(0^{\mp})\right)^{2} \right) \right]^{1/2}}, k \in \mathbb{N}^{*}, j \in \{1,2\}. $$

(66)

Also, the discrete errors on the complex variables $\left (\varphi ,\overline {\varphi }\right )$ are:

$$ \mathbf{e}_{j}^{k,m}(z) = \left( \begin{array}{c} e_{\varphi,j}^{k,m}(z) \\ e_{\overline{\varphi},j}^{k,m}(z) \end{array} \right) = \left( \begin{array}{c} \varphi_{j}^{k,m}(z) - \varphi(z,{t_{m}^{j}})\\ \overline{\varphi}_{j}^{k,m}(z) - \overline{\varphi}(z,{t_{m}^{j}}) \end{array} \right) , $$

(67)

where $\varphi _{j}^{k,m}$ and $\overline {\varphi }_{j}^{k,m}$ are defined by the Schwarz algorithm (2.3). $\mathbf {E}_{j}^{k,m}$ is linked to $\mathbf {E}_{j}^{k,m}$ by:

$$ \textbf{E}^{k,m}_{j} = \mathbf{P} \mathbf{e}_{j}^{k,m} = \frac{1}{\sqrt{2}}\begin{pmatrix} e_{\varphi,j}^{k,m} + e_{\overline{\varphi},j}^{k,m} \\ - \imath e_{\varphi,j}^{k,m} + \imath e_{\overline{\varphi},j}^{k,m} \end{pmatrix}, $$

(68)

where P is given in Section 2.2. Since P is a unitary matrix (i.e. $\mathbf {P}^{-1}=\overline {\mathbf {P}}^{T}$),

$$ \left\| \textbf{E}^{k,m}_{j} \right\|_{2}^{2} = \left( \overline{\mathbf{e}}_{j}^{k,m}\right)^{T} \overline{\mathbf{P}}^{T} \mathbf{P} \mathbf{e}_{j}^{k,m} = \left( \overline{\mathbf{e}}_{j}^{k,m}\right)^{T} \mathbf{e}_{j}^{k,m} = \left\| \mathbf{e}_{j}^{k,m} \right\|_{2}^{2}, $$

(69)

meaning that (66) becomes

$$ \mathcal{R}_{\mathbf{U}_{j}}^{k} = \frac{\left[ \underset{m=1}{\overset{M_{j}}{\sum}} \left( \left( {e}_{\varphi,j}^{k,m}(0^{\mp})\right)^{2} + \left( {e}_{\overline{\varphi},j}^{k,m}(0^{\mp})\right)^{2} \right) \right]^{1/2}} {\left[ \underset{m=1}{\overset{M_{j}}{\sum}} \left( \left( {e}_{\varphi,j}^{k-1,m}(0^{\mp})\right)^{2} + \left( {e}_{\overline{\varphi},j}^{k-1,m}(0^{\mp})\right)^{2} \right) \right]^{1/2}}, k \in \mathbb{N}^{*}, j \in \{1,2\}. $$

(70)

Let us now define $\widetilde {\rho }_{\varphi ,j}^{k,M_{j}} = \frac { \left \| \left (e_{\varphi ,j}^{k,m}(z=0^{\mp })\right ) \right \|_{2}} { \left \| \left (e_{\varphi ,j}^{k-1,m}(z=0^{\mp })\right ) \right \|_{2}} = \frac {\left [ \underset {m=1}{\overset {M_{j}}{\sum }} \left ({e}_{\varphi ,j}^{k,m}(0^{\mp })\right )^{2} \right ]^{1/2}} {\left [ \underset {m=1}{\overset {M_{j}}{\sum }} \left ({e}_{\varphi ,j}^{k-1,m}(0^{\mp })\right )^{2} \right ]^{1/2}}$ for $k \in \mathbb {N}^{*}, j \in \{1,2\}$. When $M_{j}\rightarrow +\infty$ (i.e. simulating (2.3) on a infinite time window), the temporal grid can only generate modes which frequencies lie in $I_{\omega } := \left [ -\frac {\pi }{ \underset {j \in \{1,2\}}{\textup {min}} \left \{ \delta t_{j} \right \}} ;~ \frac {\pi }{ \underset {j \in \{1,2\}}{\textup {min}} \left \{ \delta t_{j} \right \}} \right ]$. This is due to the Nyquist-Shannon sampling theorem [39]. $\widehat {\left ({e}_{\varphi ,j}^{k,m}(0^{\mp }) \right )}$ corresponds to the Fourier transform of the continuous error $\hat {e}_{\varphi }^{k}$ on I_ω. The convergence factor denoted $\widetilde {\rho }_{\varphi ,j}^{k,\infty }$ can be linked to the errors in the Fourier space by the Parseval’s theorem:

$$ \widetilde{\rho}_{\varphi,j}^{k,\infty} = \frac{ \left[ \underset{m=1}{\overset{\infty}{\sum}} ({e}_{\varphi,j}^{k,m}(0^{\mp})^{2} \right]^{1/2} } { \left[ \underset{m=1}{\overset{\infty}{\sum}} ({e}_{\varphi,j}^{k-1,m}(0^{\mp})^{2} \right]^{1/2} } = \frac{\left( {\int}_{\omega\in I} \left( \rho_{\varphi,j}^{k}(\omega)\right)^{2} \left|\hat{e}_{\varphi,j}^{k-1}(\omega)\right|^{2} d\omega\right)^{1/2}}{\left( {\int}_{\omega\in I} \left|\hat{e}_{\varphi,j}^{k-1}(\omega)\right|^{2} d\omega\right)^{1/2}}, $$

which implies that $\underset {|\omega | \leq \pi / \underset {j \in \{1,2\}}{\textup {min}} \{\delta t_{j}\}} {\textup {inf}}~\rho _{\varphi ,j}^{k}(\omega ), \le \widetilde {\rho }_{\varphi ,j}^{k,\infty } \le \underset {|\omega | \leq \pi / \underset {j \in \{1,2\}}{\textup {min}} \{\delta t_{j}\}} {\textup {sup}}~\rho _{\varphi ,j}^{k}(\omega )$. Moreover, using the identity $\displaystyle \underset {m=1}{\overset {M_{j}}{\sum }} x_{m} = \left (\underset {m=1}{\overset {\infty }{\sum }} x_{m} \right ) \left (1 - \left \{ \underset {m=M_{j}+1}{\overset {\infty }{\sum }}x_{m} \right \} / \left \{ \underset {m=1}{\overset {\infty }{\sum }}x_{m} \right \} \right )$, $\widetilde {\rho }_{\varphi ,j}^{k,M_{j}}$ can easily be linked to $\widetilde {\rho }_{\varphi ,j}^{k,\infty }$:

$$ \left( \widetilde{\rho}_{\varphi,j}^{k,M_{j}} \right)^{2} = \left( \widetilde{\rho}_{\varphi,j}^{k,\infty} \right)^{2} \frac{1-{{{\varGamma}}}_{\varphi,j}^{k,M_{j}}}{1-{{{\varGamma}}}_{\varphi,j}^{k-1,M_{j}}} \qquad\text{with } {{{\varGamma}}}_{\varphi,j}^{k,M_{j}}=\frac{\underset{m=M_{j}+1}{\overset{\infty}{\sum}} \left( e_{\varphi,j}^{k,m}(0^{\mp})\right)^{2}}{\underset{m=1}{\overset{\infty}{\sum}}\left( e_{\varphi,j}^{k,m}(0^{\mp})\right)^{2}}. $$

(71)

Since ${{{\varGamma }}}_{\varphi ,j}^{k,M_{j}}\longrightarrow 0$ as $M_{j}\rightarrow \infty$ (thanks to Section 2.1), (71) can be rewritten as $\displaystyle \widetilde {\rho }_{\varphi ,j}^{k,M_{j}} = \widetilde {\rho }_{\varphi ,j}^{k,\infty } + \mathcal {O}\left ({{{\varGamma }}}_{\varphi ,j}^{k,M_{j}}, {{{\varGamma }}}_{\varphi ,j}^{k-1,M_{j}}\right )$. Finally, the same relationships being true for $e_{\overline {\varphi },j}^{k,m}$, we end up with:

$$ \mathcal{R}_{\mathbf{U}_{j}}^{k} \leq \max \left\{ \underset{|\omega| \leq \pi / \underset{j \in \{1,2\}}{\textup{min}} \{\delta t_{j}\}} {\textup{sup}}~\rho_{\varphi,j}^{k}(\omega), ~\underset{|\omega| \leq \pi / \underset{j \in \{1,2\}}{\textup{min}} \{\delta t_{j}\}} {\textup{sup}}~\rho_{\overline{\varphi},j}^{k}(\omega) \right \} + \epsilon . $$

(72)

Proof for the upper bound (47)

In this Appendix, we provide the proof for the upper bound (47) on $\rho _{\text {DN}}^{\text {cst}}$ for constant viscosity and Dirichlet-Neumann interface conditions given in Section 4.3. We first reformulate $\rho _{\text {DN}}^{\text {cst}}$ as $\rho _{\text {DN}}^{\text {cst}} = \sqrt {\lambda }\sqrt {\frac { Q(\sqrt {2\text {Fo}_{2}})}{ Q(\sqrt {2\text {Fo}_{1}})}}$ with

$$ \mathcal{Q}(x) = \frac{ \cosh x -\cos x }{ \cosh x + \cos x }. $$

4.1 Proof for the upper bound (47) for Fo₂ < Fo₁

The derivative of $\mathcal {Q}(x)$ cancels for x^⋆ such that $\tanh (x^{\star }) + \tan (x^{\star }) = 0$. This transcendental equation has no root on [0,π/2] (and $0 \le \mathcal {Q}(x) \le 1$ on that interval) and then one root x^(⋆,k) per interval [π/2 + kπ, 3π/2 + kπ] (k ≥ 0). For even values of k, $\mathcal {Q}(x^{(\star ,k)})$ is a local maximum and $\mathcal {Q}(x) \ge 1$, while for odd values of k, $\mathcal {Q}(x^{(\star ,k)})$ is a local minimum and $\mathcal {Q}(x) \le 1$. Moreover, it can be shown that $\mathcal {Q}(x^{(\star ,0)}) > \mathcal {Q}(x^{(\star ,2)}) > \mathcal {Q}(x^{(\star ,4)}) > \hdots > 1$ and $\mathcal {Q}(x^{(\star ,1)}) < \mathcal {Q}(x^{(\star ,3)}) < \mathcal { Q}(x^{(\star ,5)}) < \hdots < 1$. This implies that the maximum of $\mathcal {Q}(x)$ is $\mathcal {Q}(x^{(\star ,0)})$ and thus that

$$ \mathcal{Q}(x) \le \mathcal{Q}(x^{(\star,0)}), \qquad x \ge 0. $$

If we now introduce $\alpha = \sqrt {\text {Fo}_{2} / \text {Fo}_{1}}$ and consider $x=\sqrt {2\text {Fo}_{1}}$, our problem is to find the upper bound of $\frac {\mathcal {Q}(\alpha x)}{ \mathcal {Q}(x) }$ with α ≤ 1 (because we consider the case Fo₂ < Fo₁ here). It is straightforward to prove that $\displaystyle \mathcal {Q}(\alpha x) \le \mathcal {Q}(x^{(\star ,0)})$, for x ≥ 0,α ≤ 1 and $\mathcal {Q}(\alpha x)$ behaves like $\mathcal {Q}(x)$ on the subintervals $[\frac {\pi }{2\alpha } + k \pi , \frac {3 \pi }{2\alpha } + k \pi ]$. We can then proceed sub-interval by sub-interval: (i) on [0,π/2] $\mathcal {Q}(x)$ increases more rapidly than $\mathcal {Q}(\alpha x)$. We thus have $\frac {\mathcal {Q}(\alpha x)}{ \mathcal {Q}(x) } \le 1$ as soon as α ≤ 1; (ii) on [π/2, 3π/2] $\mathcal {Q}(x)$ is larger than 1, meaning that $\frac {1}{\mathcal {Q}(x)} \le 1$. We thus have $\frac {\mathcal {Q}(\alpha x)}{ \mathcal {Q}(x) } \le \mathcal {Q}(x^{(\star ,0)})$ whatever the value of α; (iii) on [3π/2, 5π/2] $\mathcal {Q}(x)$ has a local minimum $\mathcal {Q}(x^{(\star ,1)})$ which is smaller than 1. We thus have $\frac {1}{\mathcal {Q}(x)} \le \frac {1}{\mathcal {Q}(x^{(\star ,1)})}$ and the worst case scenario is when this coincides with values of α such that the maximum of $\mathcal {Q}(\alpha x)$ occurs for x ∈ [3π/2, 5π/2]. We thus obtain:

$$ \frac{\mathcal{Q}(\alpha x) }{\mathcal{Q}(x) } \le \frac{\mathcal{Q}(x^{(\star,0)})}{\mathcal{Q}(x^{(\star,1)})}. $$

Because of the ordering of the values $\mathcal {Q}(x^{(\star ,k)})$ given earlier (i.e. $\mathcal {Q}(x^{(\star ,k)})$ gets closer and closer to 1 as k increases), it is not needed to go beyond x = 5π/2 since the upper bound could not be larger for x > 5π/2.

4.2 Proof for the upper bound (47) for Fo₂ ≥Fo₁

For this proof, we first study the behaviour of $\frac {\mathcal {Q}(x)}{x^{2}}$. The sign of the derivative of $\frac {\mathcal {Q}(x) }{x^{2}}$ with respect to x is the same as

$$ \cos^{2}(x)-\cosh^{2}(x)+x(\cosh(x)\sin(x)+\sinh(x)\cos(x)), $$

which is smaller or equal to zero for x ≥ 0, $\frac {\mathcal {Q}(x) }{x^{2}}$ is thus a decreasing function of x for x ≥ 0. In the case α ≥ 1 (i.e. Fo₂ ≥Fo₁) we have αx ≤ x, hence $\displaystyle \frac {\mathcal {Q}(\alpha x) }{\alpha ^{2}x^{2}}\le \frac {\mathcal {Q}(x) }{x^{2}}$ which leads to $\displaystyle \frac {\mathcal {Q}(\alpha x) }{\mathcal {Q}(x)}\le \alpha ^{2}$ where $x =\sqrt {2\text {Fo}_{1}}$ and $\alpha =\sqrt {\text {Fo}_{2}/\text {Fo}_{1}}$. We can rewrite this last inequality in terms of Fo_j to obtain

$$ \rho_{\text{DN}}^{\text{cst}}\le \sqrt{\lambda\frac{\text{Fo}_{2}}{\text{Fo}_{1}}}. $$

(73)

Note that this also proves that $\left |\mathcal {S}_{2}^{\text {cst}}(\text {Fo})\right |$ decreases, and thus $\left |\mathcal {S}_{2}^{\text {cst}}(\text {Fo})\right |\le \left |\mathcal {S}_{2}^{\text {sta, cst}}\right |=|h_{2}|$. Similarly, $\left |\mathcal {S}_{1}^{\text {cst}}(\text {Fo})\right |$ increases and $\left |\mathcal {S}_{1}^{\text {cst}}(\text {Fo})\right |\ge \left |\mathcal {S}_{1}^{\text {sta, cst}}\right |=|h_{1}|^{-1}$.

Details on sufficient conditions for RR-based SWR algorithms

5.1 Proofs of Props. 2 and 3

These proofs are based upon the following lemma:

Lemma 1

If there exists $(\gamma ^{\nu },~\sigma _{1}^{\nu },~{\Sigma }_{2}^{\nu }) \in \mathbb {R}_{+}^{3}$ such that, $\forall \omega \in \mathbb {R}$:

$$ \begin{array}{@{}rcl@{}} \forall j \in \{1,2\},~ \left|\text{Im}\left( \mathcal{S}_{j}(\omega)\right)\right| &\le& \gamma^{\nu} \left|\text{Re}\left( \mathcal{S}_{j}(\omega)\right)\right| , \end{array} $$

(74a)

$$ \begin{array}{@{}rcl@{}} \left|\text{Re}\left( \mathcal{S}_{1}(\omega)\right)\right|&\ge&\sigma_{1}^{\nu} , \end{array} $$

(74b)

$$ \begin{array}{@{}rcl@{}} \left|\text{Re}\left( \mathcal{S}_{2}(\omega)\right)\right|&\le&{\Sigma}_{2}^{\nu} , \end{array} $$

(74c)

then the following combination of conditions on $(p,q) \in \mathbb {R}_{-}^{*} \times \mathbb {R}_{+}^{*}$ guarantees the convergence of the RR-based SWR algorithm, for all $\omega \in \mathbb {R}$:

$$ -p \leq 2 \lambda \sigma_{1}^{\nu} \qquad \text{ and } \qquad q \geq \frac{1+(\gamma^{\nu})^{2}}{2}{\Sigma}_{2}^{\nu}. $$

(75)

Proof of Lemma 1

By reorganising (56), ρ_RR(p,q,ω) < 1 is equivalent to :

$$ \underbrace{pq\rho_{\text{DN}}^{2}-1 +2p\vartheta_{1}}_{\vartheta_{3}} +\underbrace{2q\text{Re}\left( \mathcal{S}_{2}\right)\left|\lambda\mathcal{S}_{1}\right|^{2}+\rho_{\text{DN}}^{2}}_{\vartheta_{4}} -q\underbrace{(p+2\text{Re}\left( \lambda\mathcal{S}_{1}\right))}_{\vartheta_{5}}<0 . $$

(76)

Since pq < 0 and per hypothesis (57), we have 𝜗₃ < 0. Let us now exploit the conditions (1) to obtain (76). Using $\rho _{DN}^{2}=|\lambda \mathcal {S}_{1}||\mathcal {S}_{2}|$, and recalling that $\text {Re}(\mathcal {S}_{2})<0$ and q > 0, then 𝜗₄ < 0 is equivalent to $-2q|\text {Re}(\mathcal {S}_{2})|+|\mathcal {S}_{2}|^{2}<0$. (74c) implies $|\mathcal {S}_{2}|^{2}\leq (1+(\gamma ^{\nu })^{2})|\text {Re}(\mathcal {S}_{2})|^{2}$. Then, $q>\frac {{{{{\varGamma }}}_{0}^{2}}}{2}|\text {Re}(\mathcal {S}_{2})|$ with ${{{\varGamma }}}_{0}=\sqrt {1+(\gamma ^{\nu })^{2}}$ implies 𝜗₄ < 0. In the same way, because q > 0 and $\text {Re}(\mathcal {S}_{1})>0$, $-p<2\lambda |\text {Re}(\mathcal {S}_{1})|$ is a sufficient condition for 𝜗₅ > 0. □

Proof of Prop. 2

As previously mentioned, we rely on Lemma 1. In the case of constant viscosities, then, using (28) and extensive reformulation (not detailed, analoguous to (46)) yields:

$$ \left| \frac{ \textup{Im}(\mathcal{S}_{j}^{\text{cst}}(\omega)) }{ \textup{Re}(\mathcal{S}_{j}^{\text{cst}}(\omega)) } \right| = \mathcal{V}(y_{j}) := \left|\frac{\sinh(y_{j})-\sin(y_{j})}{\sinh(y_{j})+\sin(y_{j})} \right| \qquad \text{with } \qquad y_{j} = \sqrt{2\textup{Fo}_{j}(\omega)}. $$

(77)

Analogously to what is done in App. 3, it can then be proved that:

$$ \forall \omega \in \mathbb{R},~ \left| \frac{ \textup{Im}(\mathcal{S}_{j}^{\text{cst}}(\omega)) }{ \textup{Re}(\mathcal{S}_{j}^{\text{cst}}(\omega)) } \right| \leq \gamma^{\text{cst}} := \mathcal{V}(y^{\star}), $$

(78)

where y^⋆ is the smallest positive root of $\tanh (y) - \tan (y) = 0$. Hence, (74a) is satisfied. Moreover, still in App. 3, it is proved that $\forall \omega \in \mathbb {R}$, $|\mathcal {S}_{1}^{\text {cst}}(\omega ) | \geq |\mathcal {S}^{\text {sta,cst}}_{1,f=0} | = 1/|h_{1}|$ and that $|\mathcal {S}_{2}^{\text {cst}}(\omega ) | \leq |\mathcal {S}^{\text {sta,cst}}_{2,f=0} | = |h_{2}|$. Hence, (74b) and (74c) can be obtained by defining:

$$ \sigma_{1}^{\text{cst}} := {\left( \sqrt{1+(\gamma^{\text{cst}})^{2}} |h_{1}| \right)}^{-1} \quad \text{ and } \quad {\Sigma}_{2}^{\text{cst}} := |h_{2}|. $$

(79)

Injecting (79) into (75), and defining ${{{\varGamma }}}_{0} := \sqrt {1+(\gamma ^{\text {cst}})^{2}}$, lead to (59). □□□

Proof Proof of Prop. 3

The proof is analogous to that of Prop. 2; hence, extensive detail is not provided. (78) still holds in that case with the same γ^cst. Moreover, since here $\omega \in I_{\omega } \subsetneq \mathbb {R}$, we know that there exists $({\Sigma }_{1}^{\text {cst}}, \sigma _{2}^{\text {cst}}) \in \mathbb {R}_{+}^{2}$ such that:

$$ \forall \omega \in I_{\omega}, \quad {\Sigma}_{1}^{\text{cst}} \geq \left|\text{Re}\left( \mathcal{S}_{1}(\omega)\right)\right| \quad \text{ and } \quad \sigma_{2}^{\text{cst}} \leq \left|\text{Re}\left( \mathcal{S}_{2}(\omega)\right)\right|. $$

(80)

Analogously to the proof of Lemma 1, and using (80), it can then be shown that (76), and thus SWR convergence, are satisfied as soon as:

$$ -p \geq \frac{1 + (\gamma^{\text{cst}})^{2}}{2} \lambda {\Sigma}_{1}^{\text{cst}} \qquad \text{ and } \qquad q \leq 2 \sigma_{2}^{\text{cst}}. $$

(81)

Moreover, since $|\text {Re}(\mathcal {S}_{1}^{\text {cst}}(\omega ))|\le |\mathcal {S}_{1}^{\text {cst}}(\omega )|$ and $\omega \mapsto |\mathcal {S}_{1}^{\text {cst}}(\omega )|$ is increasing (see App. 3), then ${\Sigma }_{1}^{\text {cst}} := |\mathcal {S}_{1}^{\text {cst}}(\omega _{\max \limits }) |$ is a suitable choice in (80). In the same way, since ${{{\varGamma }}}_{0}|\text {Re}(\mathcal {S}_{2}^{\text {cst}}(\omega ))|\ge |\mathcal {S}_{2}^{\text {cst}}(\omega )|$ and $\omega \mapsto |\mathcal {S}_{2}^{\text {cst}}(\omega )|$ is decreasing, then $\sigma _{2}^{\text {cst}} = |\mathcal {S}_{2}^{\text {cst}}(\omega _{\max \limits })| / {{{\varGamma }}}_{0}$ satisfies (80). Reinjecting this into (81) and relying on ${{{\varGamma }}}_{0} := \sqrt {1 + (\gamma ^{\text {cst}})^{2}}$ lead to (60), which, as previously mentioned, is a sufficient condition for SWR convergence with RR transmission conditions for ω ∈ I_ω. □

5.2 Discussion on Conjectures 1, 2 and 3

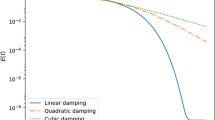
As soon as the viscosity profiles are no longer constant, the validity of (57) and (1) can only be numerically assessed. From Fig. 3 we can conjecture that $\text {Re}(\mathcal {S}_{1}^{\text {aff}} ) \ge 1$ (resp. $\text {Re}(\mathcal {S}_{1}^{\text {par}} ) \ge 1$), which suggests that (57) and (74b) are satisfied on $\mathcal {S}_{1}$. Since $\mathcal {S}_{2}(\mu ,\text {Fo}) = - |h_{2}| / (|h_{1}| \mathcal {S}_{1}(\mu ,\text {Fo}))$, this would imply that (57) and (74c) are also satisfied for $\mathcal {S}_{2}$. Figure 9 shows numerical values of $\log _{10}(\gamma )$, with $\gamma = | \textup {Im} (\mathcal {S}_{1}^{\nu }) | / | \textup {Re} (\mathcal {S}_{1}^{\nu })|$ in the cases where ν is affine and parabolic. It supports the idea that this ratio does not significantly depart from its constant viscosity value, which has been analytically found before. Then, using result from App. 3 and (4.3), we find a lower bound to $|\text {Re}(\mathcal {S}^{\nu }_{1}(\omega ))|$:

$$ |\text{Re}(\mathcal{S}^{\nu}_{1}(\omega))|\ge|\mathcal{S}^{\nu}_{1}(\omega)|{{{\varGamma}}}_{0}^{-1}=|\mathcal{R}^{\nu}_{1}(\omega)|{{{\varGamma}}}_{0}^{-1}|\mathcal{S}^{\text{cst}}_{1}(\omega)|\ge\left|\mathcal{S}^{\text{cst, sta}}_{1,f=0}\right|{{{\varGamma}}}_{0}^{-1}. $$

(82)

Analogously, an upper bound to $|\text {Re}(\mathcal {S}^{\nu }_{2}(\omega ))|$ can be found. Both bounds justify the first part of Conj. 1.

Fig. 9

Left: $\log _{10}\left [\left |\text {Im}\left (\mathcal {S}_{1}^{\text {aff}}\right )\right | \left /\left |\text {Re}\left (\mathcal {S}_{1}^{\text {aff}}\right )\right |\right ]\right .$; right: $\log _{10}\left [ \left |\text {Im}\left (\mathcal {S}_{1}^{\text {par}}\right )\right | \left /\left |\text {Re}\left (\mathcal {S}_{1}^{\text {par}}\right )\right .\right |\right ]$ with respect to Fo and μ (both axes are in logarithmic scale). The grey area corresponds to values of (Fo,μ) for which the computations of $\mathcal {S}_{1}^{aff}$ suffer from numerical instability (in the Bessel function evaluation)

If ω ∈ I_ω, then the bounds on $|\text {Re}(\mathcal {S}^{\nu }_{1}(\omega ))|$ can be adjusted:

$$ \left|\mathcal{R}^{\nu}_{1}(\omega_{\max})\right| \left|\mathcal{S}^{\text{cst,sta}}_{1,f=0}\right|{{{\varGamma}}}_{0}^{-1} \le|\text{Re}(\mathcal{S}^{\nu}_{1}(\omega))| \le|\mathcal{R}^{\nu_{1},\text{sta}}_{1, f=0}| \left|\mathcal{S}^{\text{cst}}_{1}(\omega_{\max})\right|, $$

(83)

with analogous results for $|\text {Re}(\mathcal {S}^{\nu }_{2}(\omega ))|$, hence Conj. 2.

Finally, assuming that $\omega \mapsto |\text {Re}(\mathcal {S}^{\nu }_{1}(\omega ))|$ is increasing and $\omega \mapsto |\text {Re}(\mathcal {S}^{\nu }_{2}(\omega ))|$ is decreasing, these new bounds justifying Conj. 3 can be established:

$$ \begin{array}{@{}rcl@{}} |\mathcal{S}^{\nu,sta}_{1,f=0}|{{{\varGamma}}}_{0}^{-1}\le |\text{Re}(\mathcal{S}^{\nu,sta}_{1,f=0})| \le|\text{Re}(\mathcal{S}^{\nu}_{1}(\omega))| \le|\text{Re}(\mathcal{S}^{\nu}_{1}(\omega_{\max}))| \le|\mathcal{S}^{\nu}_{1}(\omega_{\max})|, \end{array} $$

(84a)

$$ \begin{array}{@{}rcl@{}} |\mathcal{S}^{\nu}_{2}(\omega_{\max})|{{{\varGamma}}}_{0}^{-1} \le|\text{Re}(\mathcal{S}^{\nu}_{2}(\omega_{\max}))| \le |\text{Re}(\mathcal{S}^{\nu}_{2}(\omega))| \le|\text{Re}(\mathcal{S}^{\nu,sta}_{2,f=0})| \le |\mathcal{S}^{\nu,sta}_{2,f=0}|. \end{array} $$

(84b)