Skip to main content
SpringerLink
Log in

Newton-type method for solving generalized inclusion

  • Original Research
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

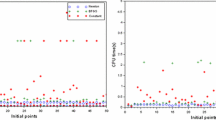
In this paper, we propose and study the problem of solve non-linear inclusion problem in Banach spaces, where the involved operator can be written as sum of a Fréchet differentiable function with a continuous perturbation. We use a specific technique introduced by Robinson (Numer. Math. 19, 341–347, 1972) to obtain Newton-Kantorovich theorem, which extends the results of Rokne (Numer. Math. 18, 401–412, 1971), for instance. In our main convergence result, we assume a kind of Hölder condition. Thus, one of the major difficulties to obtain our main result is to show that the sequence of scalars associated with the Newton sequence is convergent. Numerical examples are given to justify the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Andrew, A.L.: Error bounds for the modified Newton’s method. Bull. Austral. Math. Soc. 14(3), 427–433 (1976)

    Article  MathSciNet  Google Scholar 

  2. Argyros, I.K., Hilout, S.: On the convergence of Newton-type methods under mild differentiability conditions. Numer. Algor. 52, 701–726 (2009)

    Article  MathSciNet  Google Scholar 

  3. Argyros, I.K.: Convergence and applications of Newton-type iterations. Springer, New York (2008)

    MATH  Google Scholar 

  4. Bernard, S., Cabuzel, C., Nuiro, S.P., Pietrus, A.: Extended semismooth newton method for functions with values in a Cone. Acta Appl. Math. 155(1), 85–98 (2018)

    Article  MathSciNet  Google Scholar 

  5. Daniel, J.W.: Newton’s method for nonlinear inequalities. Numer. Math. 21, 381–387 (1973)

    Article  MathSciNet  Google Scholar 

  6. Dennis, Jr. J.E.: On the convergence of newton-like methods. In: Numerical Methods for Nonlinear Algebraic Equations (Proc. Conf., Univ. Essex, Colchester, 1969), pp 163–181. Gordon and Breach, London (1970)

  7. Dontchev, A.L., Rockafellar, R.T.: Implicit functions and solution mappings. Springer Monographs in Mathematics. Springer, Dordrecht (2009). A view from variational analysis

    Book  Google Scholar 

  8. Ferreira, O.P., Svaiter, B.F.: Kantorovich’s majorants principle for Newton’s method. Comput. Optim. Appl. 42(2), 213–229 (2009)

    Article  MathSciNet  Google Scholar 

  9. Ferreira, O.: A robust semi-local convergence analysis of Newton’s method for cone inclusion problems in Banach spaces under affine invariant majorant condition. J. Comput. Appl. Math. 279(0), 318–335 (2015)

    Article  MathSciNet  Google Scholar 

  10. Ferreira, O.P., Gonçalves, M.L.N., Oliveira, P.R.: Convergence of the Gauss-Newton method for convex composite optimization under a majorant condition. SIAM J. Optim. 23(3), 1757–1783 (2013)

    Article  MathSciNet  Google Scholar 

  11. Ferreira, O.P., Silva, G. N.: Inexact Newton’s method for nonlinear functions with values in a cone. Appl. Anal. 98(8), 1461–1477 (2019)

    Article  MathSciNet  Google Scholar 

  12. Gutierrez, J.M., Hernández, M.A.: Newton’s method under weak Kantorovich, conditions. IMA J. Numer. Anal. 20(4), 521–532 (2000)

    Article  MathSciNet  Google Scholar 

  13. He, Y., Sun, J.: Error bounds for degenerate cone inclusion problems. Math. Oper Res. 30(3), 701–717 (2005)

    Article  MathSciNet  Google Scholar 

  14. Kantorovič, L.V.: On Newton’s method for functional equations. Dokl. Akad. Nauk SSSR (N.S.) 59, 1237–1240 (1948)

    MathSciNet  Google Scholar 

  15. Kantorovich, L.V., Akilov, G.P.: Functional analysis in normed Spaces. The Macmillan Co, New York (1964)

    MATH  Google Scholar 

  16. Keller, H.B.: Newton’s method under mild differentiability conditions. J. Comput. System Sci. 4(1), 15–28 (1970)

    Article  MathSciNet  Google Scholar 

  17. Li, C., Ng, K.F.: Convergence analysis of the Gauss-Newton method for convex inclusion and convex-composite optimization problems. J. Math. Anal. Appl. 389(1), 469–485 (2012)

    Article  MathSciNet  Google Scholar 

  18. Nashed, M.Z., Chen, X.: Convergence of Newton-like methods for singular operator equations using outer inverses. Numer. Math. 66(1), 235–257 (1993)

    Article  MathSciNet  Google Scholar 

  19. Ortega, J.M., Rheinboldt, W.C.: Iterative solution of nonlinear equations in several variables. Academic Press, New York (1970)

    MATH  Google Scholar 

  20. Pietrus, A., Jean-Alexis, C.: Newton-secant method for functions with values in a cone. Serdica Math. J. 39(3-4), 271–286 (2013)

    MathSciNet  MATH  Google Scholar 

  21. Polyak, B.T.: Random algorithms for solving convex inequalities. Stud. Comput. Math. 8, 409–422 (2001)

    Article  MathSciNet  Google Scholar 

  22. Pšeničnyı̆, B.N.: A Newton method for the solution of systems of equalities and inequalities. Mat. Zametki 8, 635–640 (1970)

    MathSciNet  Google Scholar 

  23. Robinson, S.M.: Extension of Newton’s method to nonlinear functions with values in a cone. Numer. Math. 19, 341–347 (1972)

    Article  MathSciNet  Google Scholar 

  24. Robinson, S.M.: Normed convex processes. Trans. Amer. Math. Soc. 174, 127–140 (1972)

    Article  MathSciNet  Google Scholar 

  25. Rockafellar, R.T.: Monotone Processes of Convex and Concave Type. Memoirs of the American Mathematical Society, No. 77. American Mathematical Society, Providence, R.I. (1967)

    Google Scholar 

  26. Rockafellar, R.T.: Convex analysis Princeton Mathematical Series, No. 28. Princeton University Press, Princeton, N.J. (1970)

    Google Scholar 

  27. Silva, G.N., Santos, P.S.M., Souza, S. S.: Extended Newton-type method for nonlinear functions with values in a cone. Comput. Appl Math. 37 (4), 5082–5097 (2018)

    Article  MathSciNet  Google Scholar 

  28. Wang, J.H., Huang, S., Li, C.: Extended Newton’s method for mappings on Riemannian manifolds with values in a cone. Taiwan. J. Math. 13 (2B), 633–656 (2009)

    Article  MathSciNet  Google Scholar 

  29. Rokne, J.: Newton’s method under mild differentiability conditions with error analysis. Numer. Math. 18, 401–412 (1971)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We are thankful to the anonymous reviewers, and to the Associate Editor, whose comments and suggestions improved the presentation of our work.

Funding

P.S.M. Santos was supported in part by CNPq Grant 311825/2019-2. G.N. Silva was supported in part by CNPq Grant 434796/2018-2. R.C.M. Silva was supported in part by CAPES/FAPEAM Grant 062.01818/2015.

Author information

Authors and Affiliations

  1. Campus Ministro Reis Velloso, Universidade Federal do Delta do Parnaíba, Parnaíba, PI, Brazil

    P. S. M. Santos

  2. Centro das Ciências Exatas e das Tecnologias, Universidade Federal do Oeste da Bahia, CEP 47808-021, Barreiras, BA, Brazil

    G. N. Silva

  3. Departamento de Matemática, Universidade Federal do Amazonas, Manaus, AM, Brazil

    R. C. M. Silva

Authors
  1. P. S. M. Santos
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. N. Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. C. M. Silva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. S. M. Santos.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Santos, P.S.M., Silva, G.N. & Silva, R.C.M. Newton-type method for solving generalized inclusion. Numer Algor 88, 1811–1829 (2021). https://doi.org/10.1007/s11075-021-01096-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-021-01096-8

Keywords

Mathematics Subject Classification (2010)

Search

Navigation