Skip to main content
SpringerLink
Log in

Nonlinear vibration analysis of isotropic plate with inclined part-through surface crack

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

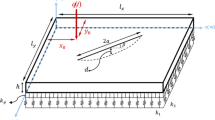
The four modes of vibration of an isotropic rectangular plate with an inclined crack are investigated. It is assumed that the crack remains continuous and its center is located at the center of the plate. The governing nonlinear equation of the transverse vibration of the plate with the plate boundary conditions being simply-supported on all edges is developed. The multiple scale perturbation method is utilized as the solution procedure to find the steady-state frequency response equations for all the four modes of vibration. The equations for the free and forced vibrations are derived and their frequency responses are presented. A special case of large-scale excitation force has also been considered. The parameter sensitivity analysis for the angle of crack, length of crack and the position of the external applied excitation force is performed. It has been shown that according to the aspect ratio of the plate, the vibration modes can have either nonlinear hardening effect or nonlinear softening behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Bauchau, O., Craig, J.: Kirchhoff plate theory. In: Structural Analysis. pp. 819–914 Springer, Berlin (2009).

  2. Bathe, K.J., Dvorkin, E.N.: A four-node plate bending element based on Mindlin/Reissner plate theory and a mixed interpolation. Int. J. Numer. Methods Eng. 21(2), 367–383 (1985)

    Article  MATH  Google Scholar 

  3. Timoshenko, S., Woinowsky-Krieger, S., Woinowsky, S.: Theory of Plates and Shells, vol. 2. McGraw-hill, New York (1959)

    Google Scholar 

  4. Rice, J., Levy, N.: The part-through surface crack in an elastic plate. J. Appl. Mech. 39, 185 (1972)

    Article  MATH  Google Scholar 

  5. Khadem, S., Rezaee, M.: An analytical approach for obtaining the location and depth of an all-over part-through crack on externally in-plane loaded rectangular plate using vibration analysis. J. Sound Vib. 230(2), 291–308 (2000)

    Article  Google Scholar 

  6. Israr, A., Cartmell, M.P., Manoach, E., Trendafilova, I., Ostachowicz, W., Krawczuk, M., Zak, A.: Analytical modelling and vibration analysis of cracked rectangular plates with different loading and boundary conditions. J. Appl. Mech. 76(1), 11005–11013 (2009)

    Article  Google Scholar 

  7. Hosseini-Hashemia, Sh, Heydar Roohi, Gh, Hossein Rokni, D.T.: Exact free vibration study of rectangular Mindlin plates with all-over part-through open cracks. Comput. Struct. 88(17), 1015–1032 (2010)

  8. Gandhi, K.R.: Analysis of an inclined crack centrally placed in an orthotropic rectangular plate. J. Strain Anal. Eng. Des. 7(3), 157–162 (1972)

    Article  Google Scholar 

  9. Huang, C., Leissa, A., Li, R.: Accurate vibration analysis of thick, cracked rectangular plates. J. Sound Vib. 330(9), 2079–2093 (2011)

    Article  Google Scholar 

  10. Ismail, R., Cartmell, M.: An investigation into the vibration analysis of a plate with a surface crack of variable angular orientation. J. Sound Vib. 331(12), 2929–2948 (2012)

    Article  Google Scholar 

  11. Yu, S.: Free flexural vibration of rectangular plates having single cracks. In: Proceedings of the 23rd International Congress of Aeronautical Sciences (ICAS), pp. 421–428 (2002).

  12. Liew, K., Hung, K., Lim, M.: A solution method for analysis of cracked plates under vibration. Eng. Fract. Mech. 48(3), 393–404 (1994)

    Article  Google Scholar 

  13. Stahl, B., Keer, L.: Vibration and stability of cracked rectangular plates. Int. J. Solids Struct. 8(1), 69–91 (1972)

    Article  MATH  Google Scholar 

  14. Krawczuk, M., Ostachowicz, W.M.: A finite plate element for dynamic analysis of a cracked plate. Comput. Methods Appl. Mech. Eng. 115(1), 67–78 (1994)

    Article  Google Scholar 

  15. Krawczuk, M.: Natural vibrations of rectangular plates with a through crack. Arch. Appl. Mech. 63(7), 491–504 (1993)

    MATH  Google Scholar 

  16. Bose, T., Mohanty, A.: Vibration analysis of a rectangular thin isotropic plate with a part-through surface crack of arbitrary orientation and position. J. Sound Vib. 332(26), 7123–7141 (2013)

    Article  Google Scholar 

  17. Ismail, R.: Vibration Analysis of a Plate with an Arbitrarily Orientated Surface Crack. University of Glasgow, Glasgow (2013)

    Google Scholar 

  18. Lu, Y., Xu, Y.: Line-spring model for a surface crack loaded antisymmetrically. National University of Defense Technology Technical Paper (1986).

  19. Joseph, P., Erdogan, F.: Surface crack in a plate under antisymmetric loading conditions. Int. J. Solids Struct. 27(6), 725–750 (1991)

    Article  Google Scholar 

  20. Zhao-Jing, Z., Shu-Ho, D.: Stress intensity factors for an inclined surface crack under biaxial stress state. Eng. Fract. Mech. 47(2), 281–289 (1994)

    Article  Google Scholar 

  21. Ansari, M., Esmailzadeh, E., Younesian, D.: Frequency analysis of finite beams on nonlinear Kelvin-Voight foundation under moving loads. J. Sound Vib. 330(7), 1455–1471 (2011)

    Article  Google Scholar 

  22. Younesian, D., Marjani, S., Esmailzadeh, E.: Nonlinear vibration analysis of harmonically excited cracked beams on viscoelastic foundations. Nonlinear Dyn. 71(1–2), 109–120 (2013)

    Article  MathSciNet  Google Scholar 

  23. Ansari, M., Esmailzadeh, E., Younesian, D.: Internal-external resonance of beams on non-linear viscoelastic foundation traversed by moving load. Nonlinear Dyn. 61(1–2), 163–182 (2010)

    Article  MATH  Google Scholar 

  24. Leung, A., Mao, S.: A symplectic Galerkin method for non-linear vibration of beams and plates. J. Sound Vib. 183(3), 475–491 (1995)

    Article  MATH  MathSciNet  Google Scholar 

  25. Fan, Z.: Transient vibration and sound radiation of a rectangular plate with viscoelastic boundary supports. Int. J. Numer. Methods Eng. 51(5), 619–630 (2001)

    Article  MATH  Google Scholar 

  26. Nayfeh, A.H.: Introduction to Perturbation Techniques. Wiley-VCH, Brikach (2004)

    Google Scholar 

  27. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley-VCH, Birkach (2004)

    Google Scholar 

  28. Kevorkian, J., Cole, J.D.: Perturbation Methods in Applied Mathematics. Springer, Berlin (1981)

    Book  MATH  Google Scholar 

  29. Murdock, J.A.: Perturbations: Theory and Methods, vol. 27. SIAM, Philadelphia (1999)

    Book  MATH  Google Scholar 

  30. Cartmell, M., Ziegler, S., Khanin, R., Forehand, D.: Multiple scales analyses of the dynamics of weakly nonlinear mechanical systems. Appl. Mech. Rev. 56(5), 455–492 (2003)

    Article  Google Scholar 

Download references

Acknowledgments

The financial support provided by the Natural Science and Engineering Research Council (NSERC) of Canada to complete this research is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Faculty of Science and Applied Science, University of Ontario Institute of Technology, Oshawa, ON, L1H 7K4, Canada

    F. Diba & E. Esmailzadeh

  2. Center of Excellence in Railway Transportation, Iran University of Science and Technology, Farjam Street, Tehran, 1684613114, Iran

    D. Younesian

Authors
  1. F. Diba
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Esmailzadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. D. Younesian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. Esmailzadeh.

Appendices

Appendices

1.1 Appendix 1

Common coefficient expressions:

$$\begin{aligned} \hat{{\mu }}_c =\frac{\mu }{2\rho h}\qquad \,\,\,\, \alpha _c =\frac{3}{2}\frac{D\pi ^{2}}{\rho h^{2}l_1^2 l_2^2 } \end{aligned}$$

Coefficients of the first mode of vibration:

$$\begin{aligned} \omega _{11}^2&= \frac{D\pi ^{4}}{\rho hl_1^2 l_2^2}\left[ 2+\frac{l_1^4 +l_2^4 }{l_1^2 l_2^2 }-2\gamma _{M_{xy} }\left( {1-\nu }\right) \right. \\&-\left. \gamma _{M{_y}} \left( {\frac{l_1^2 }{l_2^2}+\nu }\right) \right] \end{aligned}$$
$$\begin{aligned}&\alpha _{d1} =\frac{64}{3}\frac{D}{h^{2}l_1^3 l_2^3 }\frac{A_{22}}{A_{11} }\gamma _{F_{xy}}\\&\alpha _{f1} =\frac{4}{\pi ^{2}A_{11}l_1 l_2 }\sin \frac{\pi x_0 }{l_1 }\sin \frac{\pi y_0 }{l_2 }\\&\alpha _{11} =\left( {\frac{\nu l_1^2 +l_2^2 }{l_1^2 }-\gamma _{F{_y}} \frac{l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{11}^2 \\&\alpha _{12}=\left( {\frac{4\nu l_1^2 +l_2^2 }{l_1^2 }-\gamma _{F{_y }}\frac{4l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{12}^2\\&\alpha _{13} =\left( {\frac{\upsilon l_{1}^{2} +4l_2^2 }{l_1^2 }-\gamma _{F{_y}} \frac{l_1^2 +4\upsilon l_{2}^2 }{l_2^2 }}\right) A_{21}^2\\&\alpha _{14} =\left( {\frac{4\upsilon l_{1}^{2} +4l_2^2 }{l_1^2}-\gamma _{F{_y} } \frac{4l_1^2 +4\upsilon l_{2}^{2} }{l_2^2}}\right) A_{22}^2\\&\alpha _{15} =\left( {l_1^2 +\nu l_2^2 }\right) A_{11}^2 \qquad \,\,\alpha _{16}=\left( {4l_1^2 +\nu l_2^2 }\right) A_{12}^2\\&\alpha _{17}=\left( {l_1^2 +4\nu l_2^2 }\right) A_{21}^2 \qquad \,\,\alpha _{18}=\left( {4l_1^2 +4\nu l_2^2 }\right) A_{22}^2 \end{aligned}$$

Second mode coefficients:

$$\begin{aligned}&\omega _{12}^2 =\frac{D\pi ^{4}}{\rho hl_1^2 l_2^2}\left[ 8+\frac{16l_1^4 +l_2^4 }{l_1^2 l_2^2 }-8\gamma _{M_{xy} }\left( {1-\nu }\right) \right. \\&\qquad \quad -\left. \gamma _{M{_y}} \left( {\frac{16l_1^2 }{l_2^2}+4\nu }\right) \right] \\&\alpha _{d2} =\frac{64}{3}\frac{D}{h^{2}l_1^3 l_2^3 }\frac{A_{21}}{A_{12} }\gamma _{F_{xy} }\\&\alpha _{f2} =\frac{4}{\pi ^{2}A_{12}l_1 l_2 }\sin \frac{\pi x_0 }{l_1 }\sin \frac{2\pi y_0 }{l_2 }\\&\alpha _{21} =\left( {\frac{\nu l_1^2 +l_2^2 }{l_1^2 }-4\gamma _{F{_y}} \frac{l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{11}^2 \\&\alpha _{22} =\left( {\frac{4\nu l_1^2 +l_2^2 }{l_1^2 }-4\gamma _{F{_y}}\frac{4l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{12}^2\\&\alpha _{23} =\left( {\frac{\upsilon l_1^2 +4l_2^2 }{l_1^2 }-4\gamma _{F_{y} } \frac{l_1^2 +4\upsilon l_2^2 }{l_2^2 }}\right) A_{21}^2\\&\alpha _{24} =\left( {\frac{4\upsilon l_1^2 +4l_2^2 }{l_1^2 }-4\gamma _{F{_y}} \frac{4l_1^2 +4\upsilon l_2^2 }{l_2^2 }}\right) A_{22}^2\\&\alpha _{25} =\left( {l_1^2 +\nu l_2^2 }\right) A_{11}^2 \qquad \,\,\alpha _{26} =\left( {4l_1^2 +\nu l_2^2 }\right) A_{12}^2\\&\alpha _{27}=\left( {l_1^2 +4\nu l_2^2 }\right) A_{21}^2 \qquad \,\,\alpha _{28}=\left( {4l_1^2 +4\nu l_2^2 }\right) A_{22}^2 \end{aligned}$$

Coefficients of the third mode of vibration:

$$\begin{aligned}&\omega _{21}^2 =\frac{D\pi ^{4}}{\rho hl_1^2 l_2^2}\left[ 8+\frac{l_1^4 +16l_2^4 }{l_1^2 l_2^2 }-8\gamma _{M_{xy} }\left( {1-\nu }\right) \right. \\&\qquad \quad -\left. \gamma _{M{_y}} \left( {\frac{l_1^2 }{l_2^2}+4\nu }\right) \right] \\&\alpha _{d3} =\frac{64}{3}\frac{D}{h^{2}l_1^3 l_2^3 }\frac{A_{12}}{A_{21} }\gamma _{F_{xy} }\\&\alpha _{f3} =\frac{4}{\pi ^{2}A_{21}l_1 l_2 }\sin \frac{2\pi x_0 }{l_1 }\sin \frac{\pi y_0 }{l_2 }\\&\alpha _{31} =\left( {4\frac{\nu l_1^2 +l_2^2 }{l_1^2 }-\gamma _{F{_y }}\frac{l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{11}^2\\&\alpha _{32}=\left( {4\frac{4\nu l_1^2 +l_2^2 }{l_1^2 }-\gamma _{F{_y}}\frac{4l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{12}^2\\&\alpha _{33} =\left( {4\frac{\upsilon l_1^2 +4l_2^2 }{l_1^2}-\gamma _{F{_y}} \frac{l_1^2 +4\upsilon l_2^2 }{l_2^2}}\right) A_{21}^2 \\&\alpha _{34} =\left( {4\frac{4\upsilon l_1^2+4l_2^2 }{l_1^2 }-\gamma _{F{_y}} \frac{4l_1^2 +4\upsilon l_2^2}{l_2^2 }}\right) A_{22}^2\\&\alpha _{35} =\left( {l_1^2 +\nu l_2^2 }\right) A_{11}^2 \qquad \,\,\alpha _{36} =\left( {4l_1^2 +\nu l_2^2 }\right) A_{12}^2 \\&\alpha _{37}=\left( {l_1^2 +4\nu l_2^2 }\right) A_{21}^2 \qquad \,\,\alpha _{38}=\left( {4l_1^2 +4\nu l_2^2 }\right) A_{22}^2 \end{aligned}$$

Fourth mode coefficients:

$$\begin{aligned}&\omega _{22}^2 =\frac{D\pi ^{4}}{\rho hl_1^2 l_2^2}\left[ 32+16\frac{l_1^4 +l_2^4 }{l_1^2 l_2^2 }-32\gamma _{M_{xy} }\left( {1-\nu }\right) \right. \\&\qquad \quad -\left. 16\gamma _{M{_y}} \left( {\frac{l_1^2 }{l_2^2}+\nu }\right) \right] \\&\alpha _{d4}=\frac{64}{3}\frac{D}{h^{2}l_1^3 l_2^3 }\frac{A_{11} }{A_{22}}\gamma _{F_{xy} }\\&\alpha _{f4} =\frac{4}{\pi ^{2}A_{22} l_1 l_2}\sin \frac{2\pi x_0 }{l_1 }\sin \frac{2\pi y_0 }{l_2 }\\&\alpha _{41} =4\left( {\frac{\nu l_1^2 +l_2^2 }{l_1^2 }-\gamma _{F{_y} } \frac{l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{11}^2\\&\alpha _{42} =4\left( {\frac{4\nu l_1^2 +l_2^2 }{l_1^2}-\gamma _{F{_y}} \frac{4l_1^2 +\nu l_2^2 }{l_2^2 }}\right) A_{12}^2\\&\alpha _{43} =4\left( {\frac{\upsilon l_1^2 +4l_2^2 }{l_{1}^{2}}-\gamma _{F{_y}} \frac{l_1^2 +4\upsilon l_{2}^{2} }{l_{2}^{2}}}\right) A_{21}^2 \\&\alpha _{44} =4\left( {\frac{4\upsilon l_1^2 +4l_2^2 }{l_1^2}-\gamma _{F{_y}} \frac{4l_1^2 +4\upsilon l_2^2 }{l_2^2}}\right) A_{22}^2\\&\alpha _{45} =\left( {l_1^2 +\nu l_2^2 }\right) A_{11}^2 \qquad \,\,\alpha _{46} =\left( {4l_1^2 +\nu l_2^2 }\right) A_{12}^2\\&\alpha _{47}=\left( {l_1^2 +4\nu l_2^2 }\right) A_{21}^2 \qquad \,\,\alpha _{48}=\left( {4l_1^2 +4\nu l_2^2 }\right) A_{22}^2 \end{aligned}$$

1.2 Appendix 2

The procedure of deriving Eq. (15)–(18) from Eq. (1) has been presented here. In the first step, by substituting Eqs. (3), (4), (8) and (9) into Eq. (1) one will find:

$$\begin{aligned}&D\left( {\frac{\partial ^{4}w}{\partial x^{4}}+2\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+\frac{\partial ^{4}w}{\partial y^{4}}}\right) \nonumber \\&\quad =-\rho h\frac{\partial ^{2}w}{\partial t^{2}}-\mu \frac{\partial w}{\partial t}+F_x\frac{\partial ^{2}w}{\partial x^{2}} \nonumber \\&\qquad -\,\gamma _{F{_y}} F_{y} \frac{\partial ^{2}w}{\partial y^{2}}-\gamma _{M{_y}}\frac{\partial ^{2}M_y }{\partial y^{2}}-2\gamma _{M{_{xy}} } \frac{\partial ^{2}M_{xy} }{\partial x\partial y}\nonumber \\&\qquad -\,2\gamma _{F_{xy}} F_y \frac{\partial ^{2}w}{\partial x\partial y}+q_z \end{aligned}$$
(94)

Then by substituting Eqs. (5), (6), (7) and (10) into Eq. (94) leads into:

$$\begin{aligned}&D\left( {\frac{\partial ^{4}w}{\partial x^{4}}+2\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+\frac{\partial ^{4}w}{\partial y^{4}}}\right) \nonumber \\&\ =-\rho h\frac{\partial ^{2}w}{\partial t^{2}}-\mu \frac{\partial w}{\partial t}+q_z \nonumber \\&\ \ +\frac{6D}{h^{2}l_1 l_2 }\frac{\partial ^{2}w}{\partial x^{2}}\int \limits _0^{l_1 } \mathop \int \limits _0^{l_2 }\left( {\left( {\frac{\partial w}{\partial x}}\right) ^{2}+\nu \left( {\frac{\partial w}{\partial y}}\right) ^{2}}\right) \mathrm{d}x\mathrm{d}y\nonumber \\&\ \ -\gamma _{F{_y}} \frac{6D}{h^{2}l_1 l_2 }\frac{\partial ^{2}w}{\partial y^{2}}\nonumber \\&\quad \times \int \limits _0^{l_1 } \mathop \int \limits _0^{l_2 }\left( {\left( {\frac{\partial w}{\partial y}}\right) ^{2}+\nu \left( {\frac{\partial w}{\partial x}}\right) ^{2}}\right) \mathrm{d}x\mathrm{d}y \nonumber \\&\ \ +\,\gamma _{M{_y}} D\left( {\frac{\partial ^{2}w}{\partial y^{4}}+\nu \frac{\partial ^{2}w}{\partial x^{2}\partial y^{2}}}\right) \nonumber \\&\ \ +\,2\gamma _{M{_{xy}} } D\left( {1-\nu }\right) \frac{\partial ^{2}w}{\partial x^{2}\partial y^{2}} \nonumber \\&\ \ -\,\gamma _{F{_{xy}} } \frac{12D}{h^{2}l_1 l_2 }D\frac{\partial ^{2}w}{\partial x\partial y}\nonumber \\&\quad \times \mathop \int \limits _0^{l_1 } \int \limits _0^{l_2 } \left( {\left( {\frac{\partial w}{\partial y}}\right) ^{2}+\nu \left( {\frac{\partial w}{\partial x}}\right) ^{2}}\right) \mathrm{d}x\mathrm{d}y \end{aligned}$$
(95)

Based on the Galerkin’s method, the general form of the transverse deflection of the plate from Eq. (11) has been substituted into Eq. (95):

$$\begin{aligned}&D\left( \frac{\partial ^{4}X_i }{\partial x^{4}}A_{ij} Y_j \psi _{ij} (t)+2\frac{\partial ^{4}X_i Y_j }{\partial x^{2}\partial y^{2}}A_{ij} \psi _{ij} (t)\right. \nonumber \\&\quad +\left. \frac{\partial ^{4}Y_j }{\partial y^{4}}A_{ij} X_i \psi _{ij} (t)\right) \nonumber \\&\ \ =-\rho hA_{ij} X_i Y_j \ddot{\psi }_{ij} (t)-\mu A_{ij} X_i Y_j \dot{\psi }_{ij}(t) \nonumber \\&\quad +\frac{6D}{h^{2}l_1 l_2 }\frac{\partial ^{2}w}{\partial x^{2}}\int \limits _0^{l_1 } \int \limits _0^{l_2 }\left( \left( {\frac{\partial X_i }{\partial x}A_{ij} Y_j \psi _{ij} (t)}\right) ^{2} \right. \nonumber \\&\quad +\left. \nu \left( {\frac{\partial Y_j }{\partial y}A_{ij} X_i \psi _{ij} (t)}\right) ^{2}\right) \mathrm{d}x\mathrm{d}y \nonumber \\&\ \ -\gamma _{F{_y}} \frac{6D}{h^{2}l_1 l_2 }\frac{\partial ^{2}Y_j }{\partial y^{2}}A_{ij} X_i \psi _{ij} (t)\nonumber \\&\quad \times \int \limits _0^{l_1 } \int \limits _0^{l_2 } \left( \left( {\frac{\partial Y_j }{\partial y}A_{ij} X_i \psi _{ij} (t)}\right) ^{2}\right. \nonumber \\&\qquad +\left. \nu \left( {\frac{\partial X_i }{\partial x}A_{ij} Y_j \psi _{ij} (t)}\right) ^{2}\right) \mathrm{d}x\mathrm{d}y \nonumber \\&\ \ +\gamma _{M{_y}} D\left( {\frac{\partial ^{2}Y_j }{\partial y^{4}}A_{ij} X_i \psi _{ij} (t)+\nu \frac{\partial ^{2}X_i Y_j }{\partial x^{2}\partial y^{2}}A_{ij} \psi _{ij} (t)}\right) \nonumber \\&\ \ +2\gamma _{M {_{xy}} } D\left( {1-\nu }\right) \frac{\partial ^{2}X_i Y_j }{\partial x^{2}\partial y^{2}}A_{ij} \psi _{ij}(t) \nonumber \\&\ \ -\gamma _{F{_{xy}} } \frac{12D}{h^{2}l_1 l_2 }D\frac{\partial ^{2}X_i Y_j }{\partial x\partial y}A_{ij} \psi _{ij} (t)\nonumber \\&\quad \times \int \limits _0^{l_1 } \int \limits _0^{l_2 } \left( \left( {\frac{\partial Y_j }{\partial y}A_{ij} X_i \psi _{ij} (t)}\right) ^{2}\right. \nonumber \\&\qquad +\left. \nu \left( {\frac{\partial X_i}{\partial x}A_{ij} Y_j \psi _{ij} (t)}\right) ^{2}\right) \mathrm{d}x\mathrm{d}y \nonumber \\&\ \qquad +q(t)\delta \left( {x-x_0 }\right) \left( {y-y_0 }\right) \end{aligned}$$
(96)

In this Appendix the derivation of the equation of the vibration for first mode has been described in detail. The same procedure has been employed to derive the equation of the vibration for other three modes. To derived Eq. (15), the modal functions of the first mode have to be substituted in to Eq. (96). These modal functions based on the Eqs. (12) and (13) would be:

$$\begin{aligned} X_1&= \mathrm{sin}\left( {\frac{\pi x}{l_1 }}\right) \end{aligned}$$
(97)
$$\begin{aligned} Y_1&= \mathrm{sin}\left( {\frac{\pi y}{l_2 }}\right) \end{aligned}$$
(98)

By substituting Eqs. (97) and (98) into Eq. (96) and multiply by \(X_{1}Y_{1}\) and taking integral over the plate surface, one can obtain:

$$\begin{aligned}&D\frac{l_1 l_2 }{4}\left( {\frac{\pi ^{4}}{l_1^{4}}A_{11} \psi _{11}+2\frac{\pi ^{4}}{l_1^{2}l_2^{2}}A_{11} \psi _{11} +\frac{\pi ^{4}}{l_2^{4}}A_{11} \psi _{11} }\right) \nonumber \\&\quad =-\rho hA_{11} \frac{l_1 l_2 }{4}\ddot{\psi }_{11} -\mu A_{11} \frac{l_1 l_2 }{4}\dot{\psi }_{11} \nonumber \\&\qquad -\,\frac{3}{8}\frac{\pi ^{4}D}{h^{2}l_1^{3}l_2 }A_{11} \psi _{11}\nonumber \\&\qquad \times \left[ {\begin{array}{l} \left( {\nu l_1^{2}+l_2^{2}}\right) A_{11}^2 \psi _{11}^2+\left( {4\nu l_1^{2}+l_2^{2}}\right) A_{12}^2 \psi _{12}^2 \\ +\left( {\nu l_1^{2}+4l_2^{2}}\right) A_{21}^2 \psi _{21}^2\\ +\left( {4\nu l_1^{2}+4l_2^{2}}\right) A_{22}^2 \psi _{22}^2 \end{array}}\right] \nonumber \\&\qquad +\,\gamma _{F_{y}} \frac{3}{8}\frac{\pi ^{4}D}{h^{2}l_1 l_2^{3}}A_{11} \psi _{11}\nonumber \\&\qquad \times \left[ {\begin{array}{l} \left( {l_1^{2}+\nu l_2^{2}}\right) A_{11}^2 \psi _{11}^2+\left( {4l_1^{2}+\nu l_2^{2}}\right) A_{12}^2 \psi _{12}^2 \\ +\left( {l_1^{2}+4\nu l_2^{2}}\right) A_{21}^2 \psi _{21}^2\\ +\left( {4l_1^{2}+4\nu l_2^{2}}\right) A_{22}^2 \psi _{22}^2 \end{array}}\right] \nonumber \\&\qquad +\,\gamma _{M_{y}} D\frac{l_1 l_2 }{4}A_{11} \psi _{11}\left[ {\frac{\pi ^{4}}{l_1^{4}}+\nu \frac{\pi ^{4}}{l_1^{2}l_2^{2}}}\right] \nonumber \\&\qquad +\,2\gamma _{M_{xy} } D\left( {1-\nu }\right) \frac{l_1 l_2 }{4}\left[ {\frac{\pi ^{4}}{l_1^{2}l_2^{2}}}\right] \nonumber \\&\qquad -\,\gamma _{F_{xy}} \frac{16}{3}\frac{\pi ^{2}D}{h^{2}l_1^{2}l_2^{2}}A_{22} \psi _{22}\nonumber \\&\qquad \times \left[ {\begin{array}{l} \left( {l_1^{2}+\nu l_2^{2}}\right) A_{11}^2 \psi _{11}^2+\left( {4l_1^{2}+\nu l_2^{2}}\right) A_{12}^2 \psi _{12}^2\nonumber \\ +\left( {l_1^{2}+4\nu l_2^{2}}\right) A_{21}^2 \psi _{21}^2\\ +\left( {4l_1^{2}+4\nu l_2^{2}}\right) A_{22}^2 \psi _{22}^2 \end{array}}\right] \nonumber \\&\qquad +\,q(t)\mathrm{sin}\left( {\frac{\pi x_0 }{l_1 }}\right) \mathrm{sin}\left( {\frac{\pi y_0 }{l_2 }}\right) \end{aligned}$$
(99)

In the final step, by factorizing terms and cancelling \(\frac{l_1 l_2 }{4}A_{11} \pi ^{2}\) from Eq. (99) one finds:

$$\begin{aligned}&\frac{\rho h}{\pi ^{2}}\ddot{\psi }_{11}+\left[ D\left( {\frac{\pi ^{4}}{l_1^{4}}+2\frac{\pi ^{4}}{l_1^{2}l_2^{2}}+\frac{\pi ^{4}}{l_2^{4}}}\right) \right. \nonumber \\&-\gamma _{M_{y}} D\left( {\frac{\pi ^{4}}{l_1^{4}}+\nu \frac{\pi ^{4}}{l_1^{2}l_2^{2}}}\right) \nonumber \\&-\left. 2\gamma _{M_{xy} }D\left( {1-\nu }\right) \left( {\frac{\pi ^{4}}{l_1^{2}l_2^{2}}}\right) \right] \psi _{11}=-\frac{\mu }{\pi ^{2}}\dot{\psi }_{11} \nonumber \\&-\frac{3}{2}\frac{\pi ^{2}D}{h^{2}l_1^{2}l_2^{2}} \left[ \!\!{\begin{array}{l} \left( {\frac{\nu l_1^{2}+l_2^{2}}{l_1^{2}}-\gamma _{F_{y}}\frac{l_1^{2}+\nu l_2^{2}}{l_2^{2}}}\right) A_{11}^2 \psi _{11}^3\\ +\left( {\frac{4\nu l_1^{2}+l_2^{2}}{l_1^{2}}-\gamma _{F_{y}}\frac{4l_1^{2}+\nu l_2^{2}}{l_2^{2}}}\right) A_{12}^2 \psi _{11}\psi _{12}^2 \\ +\left( {\frac{\nu l_1^{2}+4l_2^{2}}{l_1^{2}}-\gamma _{F_{y}}\frac{l_1^{2}+\nu 4l_2^{2}}{l_2^{2}}}\right) A_{21}^2 \psi _{11}\psi _{21}^2\\ +\left( {\frac{4\nu l_1^{2}+4l_2^{2}}{l_1^{2}}-\gamma _{F_{y}} \frac{4l_1^{2}+4\nu l_2^{2}}{l_2^{2}}}\right) A_{22}^2 \psi _{11} \psi _{22}^2 \\ \end{array}}\!\right] \nonumber \\&-\frac{64}{3}\frac{D}{h^{2}l_1^{3}l_2^{3}}\gamma _{F_{xy}} \left[ {\begin{array}{l} \left( {l_1^{2}+\nu l_2^{2}}\right) A_{11}^2 \psi _{11}^2 \psi _{22}\\ +\left( {4l_1^{2}+\nu l_2^{2}}\right) A_{12}^2 \psi _{12}^2 \psi _{22}\\ +\left( {l_1^{2}+4\nu l_2^{2}}\right) A_{21}^2 \psi _{21}^2 \psi _{22}\\ +\left( {4l_1^{2}+4\nu l_2^{2}}\right) A_{22}^2 \psi _{22}^3 \\ \end{array}}\right] \nonumber \\&+\frac{4}{\pi ^{2}A_{11} l_1 l_2 }q(t)\mathrm{sin}\left( {\frac{\pi x_0 }{l_1 }}\right) \mathrm{sin}\left( {\frac{\pi y_0 }{l_2 }}\right) \end{aligned}$$
(100)

The coefficients of Eq. (100) have been listed in Appendix I.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Diba, F., Esmailzadeh, E. & Younesian, D. Nonlinear vibration analysis of isotropic plate with inclined part-through surface crack. Nonlinear Dyn 78, 2377–2397 (2014). https://doi.org/10.1007/s11071-014-1595-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1595-7

Keywords

Search

Navigation